线性规划问题及灵敏度分析在 LINGO 软件中的实现 （龙少波 李东阳 罗添元） 一、问题的提出： 某公司饲养实验用的动物以出售给动物研究所，已知这些动物的生长对饲 料中 3 种营养成分（蛋白质、矿物质和维生素）特别敏感，每个动物每周至少需 要蛋白质 60g，矿物质 3g，维生素 8mg，该公司能买到 5 种不同的饲料，每种饲 料 1kg所含各种营养成分和成本如下表所示，如果每个小动物每周食用饲料不超 过 52kg，才能满足动物生长需要。 A1 A2 A3 A4 A5 蛋白质(g) 矿物质(g) 维生素(mg) 成本（元/ kg） 0.3 0.1 0.05 0.2 2 0.05 0.1 0.7 1 0.02 0.02 0.4 0.6 0.2 0.2 0.3 1.8 0.05 0.08 0.5 营养最 低 要 求 60 3 8 问题： 1．求使得总成本最低的饲料配方？ 2．如果另一个动物研究对蛋白质的营养要求变为 59 单位， 但是要求动物的价格比现在的价格便宜 0.3 元，问该养殖所 值不值得接受？ 3．由于市场因素的影响，X2 的价格降为 0.6 元每千克， 问是否要改变饲料配方？ 二、建立线性规划数学模型 解答： （1）设需要饲料 A1, A2, A3, A4 分别为 X1, X2, X3, X4kg，则建立线 性规划数学模型如下： 目标函数：MinS=0.2X1+0.7X2+0.4X3+0.3X4+0.5X5 约束条件：0.3X1+2X2+X3+0.6X4+1.8X5>=60 0.1X1+0.05X2+0.02X3+0.2X4+0.05X5>=3 005X1+0.1X2+0.02X3+0.2X4+0.08X5>=8 

X1+X2+X3+X4+X5<=52 X1, X2, X3, X4, X5>=0 三、在 LINGO 软件中的求解 在 LINGO 中输入下面的命令： Model： Min=0.2*x1+0.7*x2+0.4*x3+0.3*x4+0.5*x5; 0.3*x1+2*x2+x3+0.6*x4+1.8*x5>60; 0.1*x1+0.05*x2+0.02*x3+0.2*x4+0.05*x5>3; 0.05*x1+0.1*x2+0.02*x3+0.2*x4+0.08*x5>8; x1+x2+x3+x4+x5<52; end 操作：选菜单 Lingo|Solve(或按 Ctrl+S),或用鼠标点击“求解”按纽， 如果模型有语法错误，则弹出一个标题为“LINGO Error Message”(错 误信息)的窗口，指出在哪一行有怎样的错误，每一种错误都有一个 编号（具体含义可查阅相关文献或 LINGO 的 Help）.改正错误以后再 求解，如果语法通过，LINGO 用内部所带的求解程序求出模型的解， 然后弹出一个标题为“LINGO Solver Status”（求解状态）的窗口，其 内容为变量个数、约束条件个数、优化状态、耗费内存、所花时间等 信息，点击 Close 关闭窗口，屏幕上出现标题为“Solution Report”（解 的报告）的信息窗口，显示优化计算（线性规划中换基迭代）的步数、 优化后的目标函数值、列出各变量的计算结果. 输出结果如下: Global optimal solution found at iteration: 4 Objective value: Variable X1 X2 X3 X4 X5 22.40000 Value 0.000000 12.00000 0.000000 30.00000 10.00000 Reduced Cost 0.7000000 0.000000 0.6166667 0.000000 0.000000 

Row 1 2 3 4 5 Slack or Surplus 22.40000 0.000000 4.100000 0.000000 0.000000 四、结果分析： (一) 一般分析 Dual Price -1.000000 -0.5833333 0.000000 -4.166667 0.8833333 1.因此,每周每个动物的配料为饲料 A2、A4、A5 分别为 12、30 和 10kg，合计为 52KG，可使得饲养成本达到最小，最小成本为 22.4 元； 2. “Reduced Cost”表示当变量有微小变动时, 目标函数的变化 率。其中基变量的 reduced cost 值应为 0，对于非基变量 Xj, 相应的 reduced cost 值表示当某个变量 Xj 增加一个单位时目标函数增加的 量。变量 X1 对应的 reduced cost 值为 0.7，表示当非基变量 x1 的值 从 0 变为 1 时（此时假定其他非基变量保持不变,但为了满足约束条 件，基变量显然会发生变化），最优的目标函数值 = 22.4+0.7 = 23.1。 3. “Slack or Surplus”给出松驰变量的值：可以看出，蛋白质和维 生素刚达到最低标准，矿物质超过最低标准 4.1g； 4. “DUAL PRICE”（对偶价格）表示当对应约束有微小变动时, 目标函数的变化率。输出结果中对应于每一个约束有一个对偶价格。 若其数值为 p， 表示对应约束中不等式右端项若增加 1 个单位，目 标函数将增加 p 个单位（max 型问题）。显然，如果在最优解处约束 正好取等号（也就是“紧约束”，也称为有效约束或起作用约束），对 偶价格值才可能不是 0. 从“Dual Price”可以得到: 1.降低标准蛋白质 1 单位可使饲养成本降低 0.583 元，（第二个 问题答案） 2.降低标准维生素 1 单位可使饲养成本降低 4.167 元， 3.降低矿物质的标准不会降低饲养成本， 4.如果动物的进食量减少，就必须选取精一些的饲料但要增加 成本，大约进食量降低 1kg 可使得饲养成本增加 0.88 元. （二）灵敏度分析 

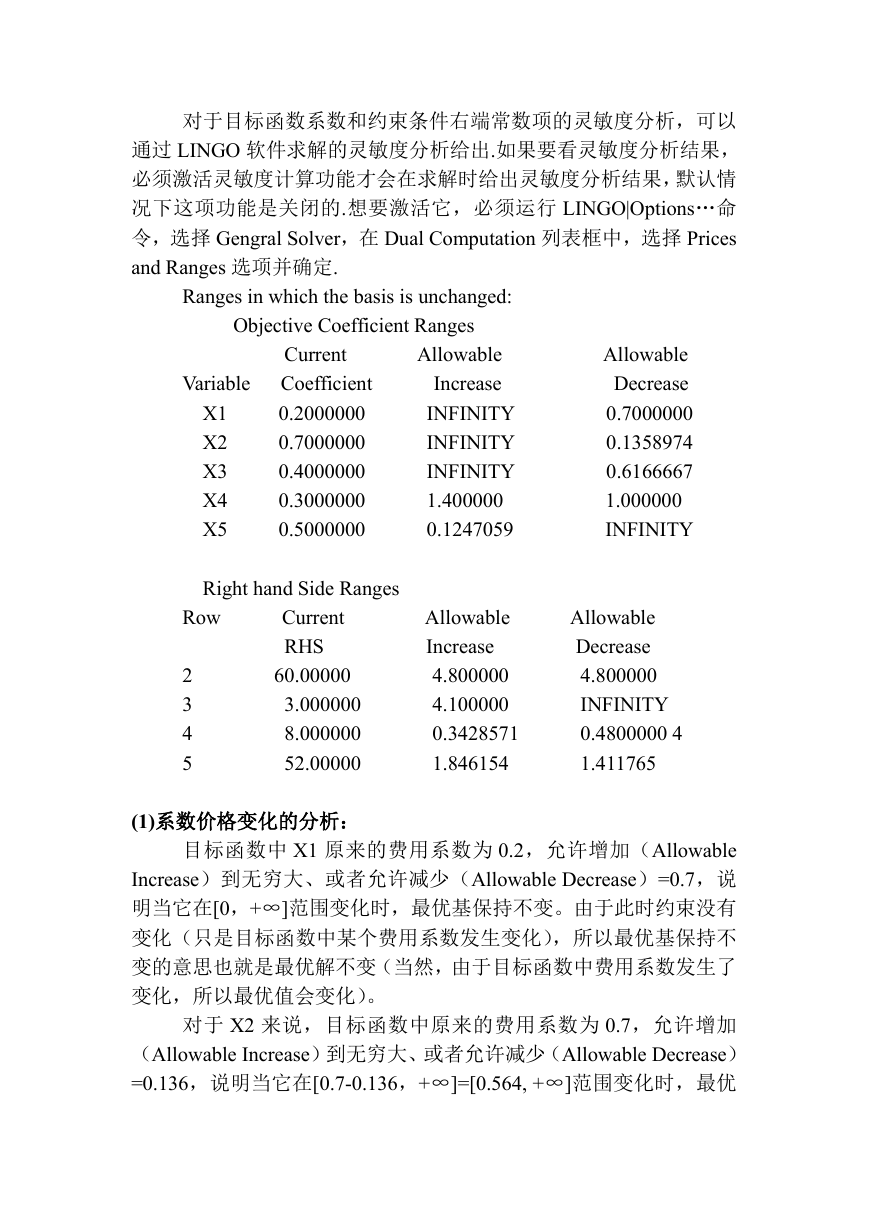
对于目标函数系数和约束条件右端常数项的灵敏度分析，可以 通过 LINGO 软件求解的灵敏度分析给出.如果要看灵敏度分析结果， 必须激活灵敏度计算功能才会在求解时给出灵敏度分析结果，默认情 况下这项功能是关闭的.想要激活它，必须运行 LINGO|Options…命 令，选择 Gengral Solver，在 Dual Computation 列表框中，选择 Prices and Ranges 选项并确定. Ranges in which the basis is unchanged: Objective Coefficient Ranges Variable X1 X2 X3 X4 X5 Current Coefficient 0.2000000 0.7000000 0.4000000 0.3000000 0.5000000 Right hand Side Ranges Row 2 3 4 5 Current RHS 60.00000 3.000000 8.000000 52.00000 Allowable Increase INFINITY INFINITY INFINITY 1.400000 0.1247059 Allowable Increase 4.800000 4.100000 0.3428571 1.846154 Allowable Decrease 0.7000000 0.1358974 0.6166667 1.000000 INFINITY Allowable Decrease 4.800000 INFINITY 0.4800000 4 1.411765 (1)系数价格变化的分析： 目标函数中 X1 原来的费用系数为 0.2，允许增加（Allowable Increase）到无穷大、或者允许减少（Allowable Decrease）=0.7，说 明当它在[0，+∞]范围变化时，最优基保持不变。由于此时约束没有 变化（只是目标函数中某个费用系数发生变化），所以最优基保持不 变的意思也就是最优解不变（当然，由于目标函数中费用系数发生了 变化，所以最优值会变化）。 对于 X2 来说，目标函数中原来的费用系数为 0.7，允许增加 （Allowable Increase）到无穷大、或者允许减少（Allowable Decrease） =0.136，说明当它在[0.7-0.136，+∞]=[0.564, +∞]范围变化时，最优 

基保持不变。（第三个问题答案） （2）约束中右端项变化的分析： 第 2 行约束中右端项（Right Hand Side，简写为 RHS）原来为 60，当它在[60-4.8，60+4.8] = [55.2，64.8]范围变化时，最优基保持 不变。第 3、4、5 行可以类似解释。不过由于此时约束发生变化，最 优基即使不变，最优解、最优值也会发生变化。