logo资料库

CST MWS里面瞬态求解器的设置-accuracy的设置.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.74M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    CST MWS 里面瞬态求解器的设置-accuracy 的设置 一、 问题的提出： 1. CST 软件里面瞬态求解器的设置----精度 accuracy 的设置：它的设置有 20， -30，-40，-50......-80dB （1）一般的理论验证或者仿真将其设置为多少？-30dB （2）如果是做一些实际的产品，又设置为多少？-60dB （3）还是根据具体的模型或产品要求，自己选择适当的档，怎么判断？ （4）精度设置的越高-80dB，计算的时间越长，也就是效率不是最佳，怎么设 置才能达到最佳设置？ （5） Accuracy 这个参数对仿真结果（S 参数）有什么影响？为什么？ （6）Accuracy 这个参数对仿真时间有什么影响？为什么？ （7） “精度”的定义是什么？ （8）在 CST MWS 中要得到“准确的”仿真结果，最重要的参数是什么？ （9）在 CST MWS 仿真中，“最佳”的定义是什么？ 图 1 ＣＳＴ ＭＷＳ瞬态求解器的设置
    二、 问题的解答 １.Accuracy 这个参数对仿真结果（S 参数）的影响，我认为是如果曲线-30dB 是收敛的话，采用-40dB 以后的值，其 S 参数是一样的，如果-30dB 情况下，没 有收敛的话，Accuracy 参数取其他值，其 S 参数曲线是不一样的，个人认为， 取更高精度值， ２. Accuracy 这个参数对仿真时间有影响，值取得越大，计算时间越长。因为软 件会按照你设定的条件进行判断。 ３. “精度”的定义，个人认为不是准确度，我认为精度是指：计算模型的离散化 程度，网格加密的程度，delta S 应该可以认为是精度的概念，其值越小，计算 时间越长，结果更为可信。 ４.在 CST MWS 中要得到“准确的”仿真结果，重要的参数是 delta S 的值范围， ５. 在 CST MWS 仿真中，“最佳”的定义，我的意思是这个求解器怎么设置，或 者说上图的一些参数应该怎么设置，使最终的 S 参数更准确，在计算时间不是 很长的情况下，在能得到准确的结果的情况下，上述图中的参数应该怎么设置？ 也就是得到一组最佳的设置，即效率高一点。 最终的问题就是求解器怎么样设 置，以此来取得准确的 S 参数值。 ６.准确的 S 参数值，我不是指理论上的精度最高的值，而是在理论上或可以实 际应用的值。 ７.Transient Solver 里的 Accuracy 这个参数通过 Steady State Monitor 监控激 励函数结 束之后 模型中 剩余 能量 与 初 始能 量的比 值 ，在 Maximum solver duration 之内，如果剩余能量与初始能量的比值小于 Accuracy 的设定值，那么 求解器就终止仿真。终止仿真时，模型中剩余能量被视为“数值噪声（Numerical Noise）”。在这里，可以把 accuracy 的这个值变相地理解为“信噪比”。假设 accuracy 分别被设置为-30 dB 和-50 dB，那么后者在结束仿真时可以理解为比 前者的数值噪声功率低 20 dB。因此，-50 dB 的情况下，得到的结果可以更“准 确地”将“小信号”从噪声中“提取”出来。 ８.举个例子，这是一个 8P8C 的连接头的模型，比较-30 dB 和-80 dB 条件下的 Return Loss： -30 dB 图 ２
    图 ３ 可以看到，100 - 1000 MHz 之间的数值几乎完全一致，但是明显可以观察 到低频部分（0 - 100 MHz）的差别。-30 dB 情况下，低频部分的回波损耗值很 小，因此被“淹没”在数值噪声之中了。在-80 dB 的情况下，数值噪声的水平被进 一步降低，因此能把很微弱的信号从噪声中提取出来。 ９. Accuracy 对 S 参数的影响，即该参数只影响 S 参数中“很小的数值”的“准确 性”。对于已经能从数值噪声中被分辨出来的数值，降低 Accuracy 的数值不能再 进一步提高“准确性”。而且，这个参数完全不影响数值的“正确性”，例如谐振点 频率等等。 １０.Accuracy 决定仿真数值噪声的水平，因此参数值越低，求解器需要更长的 时间将模型中的能量消逝出去。 １１.说到“精度”，个人觉得很多人都在乱用这个定义。在物理学里，描述一个测 量值和理论真值的接近程度使用两种参数：准确度和精密度。在仿真里，个人认 为绝大多数人所说的“精度”其实都说的是“准确度”（注意，不是上面我们所说的 accuracy 这个参数）。CST MWS 中，决定仿真结果和理论真值的接近程度的因 素只有一个：网格划分。网格化分得越细致，仿真结果就越接近理论真值。 １２．所以，如果追求的是仿真结果接近“理论真值”，需要关注网格划分是否合 理，和求解器里的 Accuracy 参数无关。 １３．在仿真中，没有“最佳”这种概念，有的只是“合理”。想得到更准确地结果， 需要消耗更多的硬件资源和仿真时间；想要节省资源缩短仿真时间，必定要牺牲 仿真结果的准确程度。因此，仿真需要考虑的只是如何平衡这两方面的需求，做 到合理即可。 １４．我个人认为 Accuracy 对 S 参数的影响，我仿真过的一些模型， （1）对于简单模型而言，其 S 参数曲线在-30dB，-40db，-60dB 的曲线一样， 这 是 在 不 自 适 应 网 格 的 情 况 下 的 结 果 ， 个 人 认 为 这 种 简 单 模 型 不 能 说 明 Accuracy 对 S 参数的影响， （2）对于复杂的模型而言，有的模型的 S 参数曲线在-30dB，-40dB，-60dB， -80dB 下的曲线完全不一样，这也是在不自适应网格的情况下，对上述（2）里 面的结果比对，哪一个更好？，那是不是其绝对值越大的数，结果更为可信，但 是时间会相应的增加很多，这样就不是很合理，这一点我也不是很明白，个人会 采用更高 accuracy 值得结果曲线。
    （3）对于简单模型或者复杂的模型，先采用自适应网格加密，然后在 accuracy 的参数选取其他的值，其结果相差不是很大； 对于上述情况的分析，个人认为在（3）这种情况下，对 accuracy 的不同参数值 进行结果和时间比较，选取一个比较合理的参数值。 １５．对于说到“精度”，个人觉得很多人都在乱用这个定义。在物理学里，描述 一个测量值和理论真值的接近程度使用两种参数：准确度和精密度。在仿真里， 个人认为绝大多数人所说的“精度”其实都说的是“准确度”（注意，不是上面我们 所说的 accuracy 这个参数）。CST MWS 中，决定仿真结果和理论真值的接近程 度的因素只有一个：网格划分。网格化分得越细致，仿真结果就越接近理论真值。 １６．对于这个问题：Delta S 是指在 Adaptive mesh refinement 里的 delta S， 它是关系到网格化分细致与否的问题。delta S 可以手动设置，默认设置是 0.02. 如果需要很高的精度（或者说是准确度）也可以设置为 0.002 或 0.001 之类的， 当然这样仿真的时间将会很长，以牺牲时间为代价，numbers of pass 的值也可 以相应设置大一点，个人认为这和 HFSS 软件里面的设置及原理差不多。 １７． 对于我开始提出的问题，就是怎么设置才能达到一个好的结果，即就是 一个合理的设置，个人认为可以按照 2.里面的方法进行。 １８．我想先强调一下我的一个观点：仿真结果是否正确，唯一的判定原则就是 网格划分，与 accuracy 这个参数无关。 １９．如果是简单的模型，很可能模型本身不存储能量（无谐振）。假设这个模 型在一个脉冲时间之内剩余能量就已经耗散至输入能量的-60 dB 以下，那么 accuracy 设置多少没有任何区别。 ２０．如果是复杂模型，模型有可能带有谐振，模型有可能有很长的传输长度， 在能量耗散缓慢的前提下，在不同的数值噪声水平结束仿真就会引入不同程度的 截断误差，导致 S 参数曲线产生不同程度的波纹。楼主提到你的“复杂”模型，并 没有说明是什么样的复杂模型，并没有说明能量耗散得慢的原因何在，并没有说 明“曲线完全不一样”是什么样的“完全不一样”，并没有说明极大值（最大值）数 值或者谐振点频率是否改变。因此，这里只能说，对“复杂”模型调整 accuracy 只是改变了截断误差，变更了仿真时间。没有网格的相关信息，哪一个结果都没 有“可信度”，accuracy 对仿真结果的“正确性”与否没有任何关系。 ２１．对模型使用自适应加密，这属于网格的范畴。运行过自适应加密并且完成 运算，说明软件已经判定网格划分已经达到要求，对于给定的模型以及参数设置， 仿真出来就应该是这样的数值。换句话说，仿真结果的“正确性”已经有了保证。 在这个前提下，改变 accuracy 不会进一步提高“正确性”，改变的仍然只是截断 误差对 S 参数曲线的影响而以。 ２２．在自适应网格优化中可以手动修改 delta S，这影响自适应优化结束的条 件。毕竟网格优化时系统资源的消耗并不是完全线性增长的，加密次数越多，消
    耗的资源增长的就越夸张。因此，这仍然是一个平衡的问题：在增加网格数目接 近理论真值和节省系统资源之间寻找平衡点。以个人的经验，没必要调整这个参 数值。 ２３．以我个人的经验，要得到“好”的结果，好好在网格划分上多下些功服，这 才是最重要的。Accuracy 这个参数就是用来控制仿真时间的，计算得“对”与“错” 与它无关。 ２４． 调整 accuracy 改变了截断误差，变更了仿真时间,改变的是截断误差对 S 参数曲线的影响. 图 ４ 输入信号 （1) 图 1 中一个四端口的网络，图中的信号是，一端口输入，四端口输出的端 口信号，采用-30dB 的 accuracy 时，此信号在 11.5ns 被截断，但是其后面还有 信号，过早的截断信号，造成 S41 参数不完整，也就造成曲线不一样。 （2）图 2 显示的是-80dB 的 accuracy 的 o4,1 的端口信号，这个信号最早完成 图 ５
    也是在 17ns 的位置，也就是图 1 中把 11.5ns--17ns 之间的信号直接忽略了，从 而造成-30dB，-60dB，-80dB 的 accuracy 的参数下，S41 参数曲线不一样。 图 ６ （3）因为我关注的是 S41 的结果 （4）对于图 3 中数据就是改变 accuracy 的值，造成 S41 参数曲线不一样。 图 ７ （5）同样的情况下，当加上自适应网格后，采用不同的 accuracy 参数值，同样 造成 S41 参数曲线不一样，在此我就不贴这张图了。
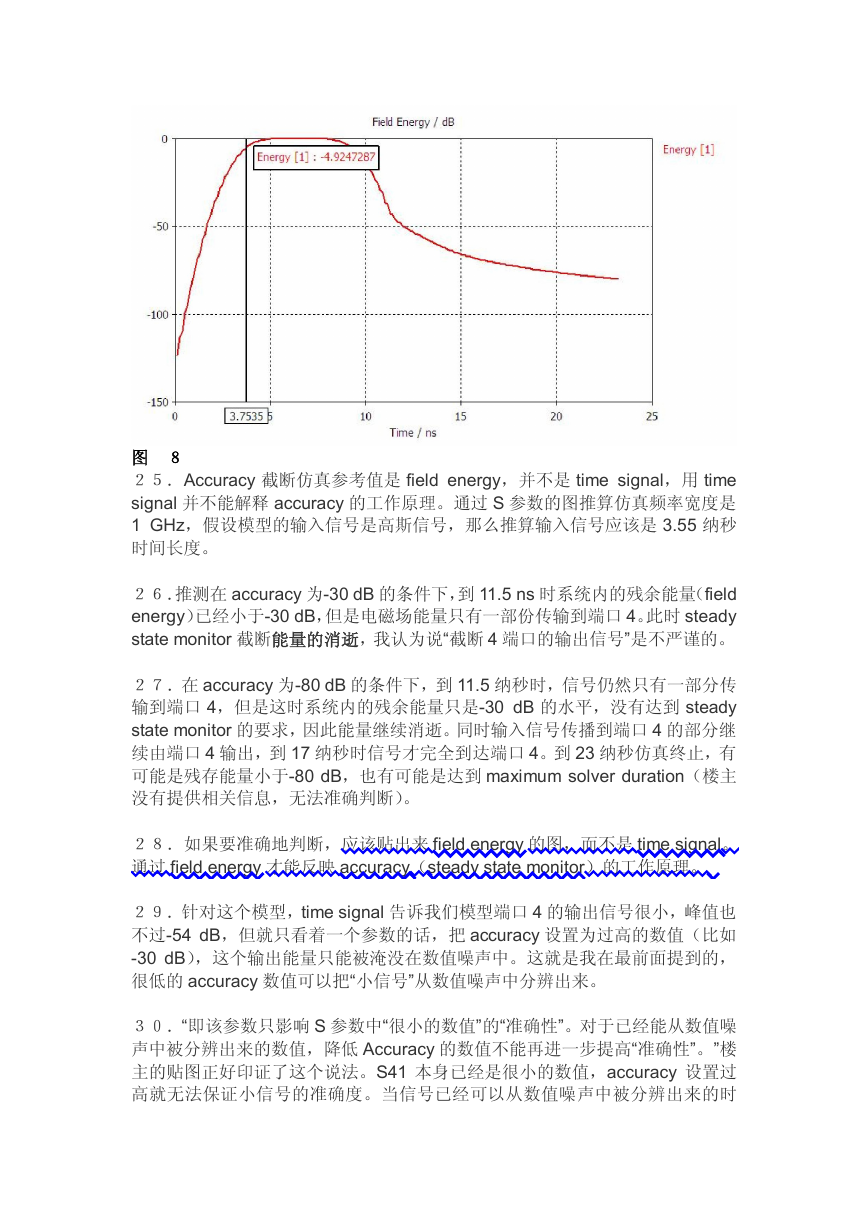
    图 ８ ２５．Accuracy 截断仿真参考值是 field energy，并不是 time signal，用 time signal 并不能解释 accuracy 的工作原理。通过 S 参数的图推算仿真频率宽度是 1 GHz，假设模型的输入信号是高斯信号，那么推算输入信号应该是 3.55 纳秒 时间长度。 ２６．推测在 accuracy 为-30 dB 的条件下，到 11.5 ns 时系统内的残余能量（field energy）已经小于-30 dB，但是电磁场能量只有一部份传输到端口 4。此时 steady state monitor 截断能量的消逝，我认为说“截断 4 端口的输出信号”是不严谨的。 ２７．在 accuracy 为-80 dB 的条件下，到 11.5 纳秒时，信号仍然只有一部分传 输到端口 4，但是这时系统内的残余能量只是-30 dB 的水平，没有达到 steady state monitor 的要求，因此能量继续消逝。同时输入信号传播到端口 4 的部分继 续由端口 4 输出，到 17 纳秒时信号才完全到达端口 4。到 23 纳秒仿真终止，有 可能是残存能量小于-80 dB，也有可能是达到 maximum solver duration（楼主 没有提供相关信息，无法准确判断）。 ２８．如果要准确地判断，应该贴出来 field energy 的图，而不是 time signal。 通过 field energy 才能反映 accuracy（steady state monitor）的工作原理。 ２９．针对这个模型，time signal 告诉我们模型端口 4 的输出信号很小，峰值也 不过-54 dB，但就只看着一个参数的话，把 accuracy 设置为过高的数值（比如 -30 dB），这个输出能量只能被淹没在数值噪声中。这就是我在最前面提到的， 很低的 accuracy 数值可以把“小信号”从数值噪声中分辨出来。 ３０．“即该参数只影响 S 参数中“很小的数值”的“准确性”。对于已经能从数值噪 声中被分辨出来的数值，降低 Accuracy 的数值不能再进一步提高“准确性”。”楼 主的贴图正好印证了这个说法。S41 本身已经是很小的数值，accuracy 设置过 高就无法保证小信号的准确度。当信号已经可以从数值噪声中被分辨出来的时
    候，以楼主贴图的范例：-60 dB 和-80 dB 的情况下，accuracy 已经不会在显著 的影响结果的准确度了，两条曲线已经很接近了。 ３１．自适应与否牵扯的是仿真结果是否接近理论真值的问题，和 accuracy 不 相关。 ３２．具体问题需要具体分析。 （１）以图７为例，如果感兴趣的参数就是 S41，如果感兴趣的频率范围就是 1.6-2.6 GHz，那么-50 dB 以下的数值决定了“要想得到‘准确的’S41 模值就必须 使用偏小的 accuracy 设置”。这是由你的这个模型的特性决定的。 （２）如果是我来处理，我会考虑先在低网格数的情况下尝试不同的 accuracy 设置，对比得到的 S41，保证 S41 曲线的“正确性”。比如尝试从-20 dB 到-80 dB， S41 的变化应该像-60 dB 和-80 dB 那样基本不变，不能出现-30 dB 的情况。还 可以继续尝试-50 dB、-40 dB 等等，直到找到能保证曲线相似性的最大设置值。 接下来在这个 accuracy 的前提下，再进行网格优化。 以上是自己的一些看法，不值准确与否，难免有很多错误，希望大家批评指正， 仅供参考； 本文的完成感谢微波仿真论坛的管理员ｈｅｆａｎｇ的详细解答， ｃｚｌａｌｖｉｎ ２０１１－１１－１４
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料