2010年云南昭通中考数学真题及答案.doc-资料库

第1页 / 共16页

第2页 / 共16页

第3页 / 共16页

第4页 / 共16页

第5页 / 共16页

第6页 / 共16页

第7页 / 共16页

第8页 / 共16页

2010年云南昭通中考数学真题及答案（全卷三个大题，共 23 个小题，共 6 页；满分 120 分，考试用时 120 分钟）注意事项： 1. 本卷为试题卷，考生必须在答题卷上解题作答，答案书写在答题卷相应位置上，在试题卷、草稿纸上作答无效． 2. 考试结束后，请将试题卷和答题卷一并交回．一、选择题（本大题共 7 小题，每小题只有一个正确先项，每小题 3 分，满分 21 分） 1. 下列结论错误的是 A． 4 2 Ｂ．方程2x 4 0 的解为 x 2 Ｃ． (a b)(a b) 2 a 2 b Ｄ． 2x y 2xy 2. 下列图形是轴对称图形的是Ａ．Ｂ．Ｃ．Ｄ． 3. 下列运算正确的是 2 3 A． x ·x 3 a 5 a 5 x Ｂ． (a b) 2 2 a 2 b 2 Ｃ． (a 3 ) 5 a 2 Ｄ． a 4. 下列事件中是必然事件的是 A．一个直角三角形的两个锐角分别是40°和 60° Ｂ．抛掷一枚硬币，落地后正面朝上 2 Ｃ．当 x 是实数时， x ≥0 Ｄ．长为5cm 、5cm 、11cm 的三条线段能围成一个三角形

5. 某物体的三视图如图 1 所示，那么该物体的形状是 A．圆柱Ｂ．球Ｃ．正方体Ｄ．长方体图 1 图 2 6. 如图 2， AB∥CD ， EF AB 于 E ， EF 交CD 于 F ，已知 2 30°，则 1 是 A． 20° Ｂ． 60° Ｃ． 30° Ｄ． 45° 7. 二次函数 y 2 ax bx c的图象如图3 所示，则下列结论正确的是 A． a 0，b 0，c 2 0，b 4ac 0 Ｂ． a 0，b 0，c 2 0，b 4ac Ｃ． a 0，b 2 0，c 0，b 4ac 0 0 Ｄ． a 0，b 0，c 2 0，b 4ac 0 二、填空题（本大题共 8 小题，每小题 3 分，满分 24 分） 8. 3 的相反数是． 9．计算： ( 0 3) 1 ． 2 10. 分解因式： 3a b 4ab ．图 3 11. 如图 4，上海世博会的中国馆建筑外观以“东方之冠，鼎盛中华，天下粮仓，富庶百姓”为构思主题，建筑面积 4.6457 万平方米，保留两个有效数字是万平方米． 12. 不等式 1 2 x 3 ≤0 的解集为．

图 4 图 5

13. 如图 5，⊙O的弦 AB 8 ，M 是 AB 的中点，且OM 为 3 ，则⊙O的半径为． 14. 如果两个相似三角形的一组对应边分别为 3cm 和 5cm ，且较小三角形的周长为15cm ，则较大三角形的周长为 cm ． 15 ．某种火箭被竖直向上发射时，它的高度 h(m) 与时间 t(s) 的关系可以用公式 h 2 5t 150t 10 表示．经过 s ，火箭达到它的最高点．三、解答题（本大题共 8 小题，满分 75 分） 16．（7 分）先化简再求值：，其中 x 5 ． x 2x 2 x 3 4 9 x 2 17．（8 分）如图 6， ABCD 的两条对角线 AC 、 BD 相交于点O ．（1）图中有哪些三角形是全等的？（2）选出其中一对全等三角形进行证明．图 6

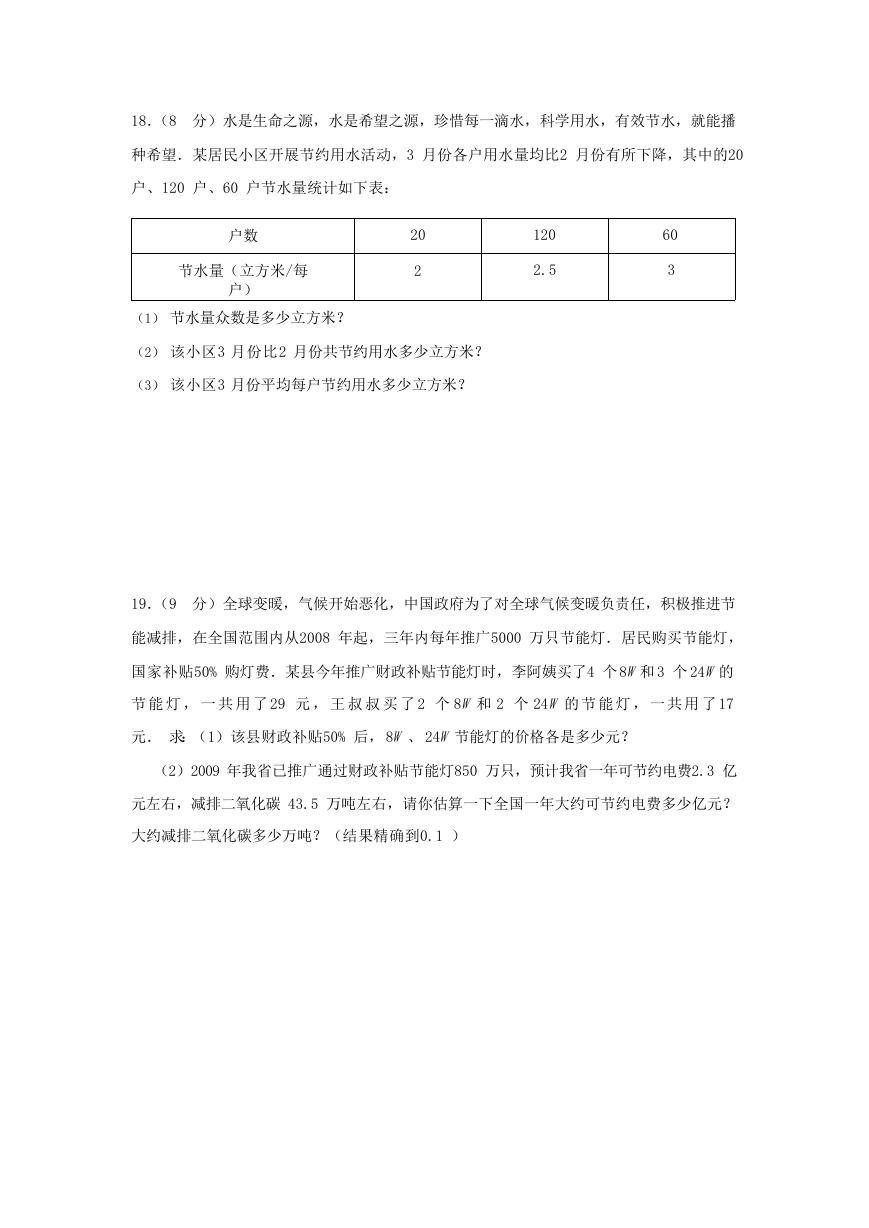
18．（8 分）水是生命之源，水是希望之源，珍惜每一滴水，科学用水，有效节水，就能播种希望．某居民小区开展节约用水活动，3 月份各户用水量均比2 月份有所下降，其中的20 户、120 户、60 户节水量统计如下表：户数节水量（立方米/每户） 20 2 120 2.5 60 3 （1）节水量众数是多少立方米？（2）该小区3 月份比2 月份共节约用水多少立方米？（3）该小区3 月份平均每户节约用水多少立方米？ 19．（9 分）全球变暖，气候开始恶化，中国政府为了对全球气候变暖负责任，积极推进节能减排，在全国范围内从2008 年起，三年内每年推广5000 万只节能灯．居民购买节能灯，国家补贴50% 购灯费．某县今年推广财政补贴节能灯时，李阿姨买了4 个 8W 和 3 个 24W 的节能灯，一共用了 29 元，王叔叔买了 2 个 8W 和 2 个 24W 的节能灯，一共用了 17 元．求：（1）该县财政补贴50% 后， 8W 、 24W 节能灯的价格各是多少元？（2）2009 年我省已推广通过财政补贴节能灯850 万只，预计我省一年可节约电费2.3 亿元左右，减排二氧化碳 43.5 万吨左右，请你估算一下全国一年大约可节约电费多少亿元？大约减排二氧化碳多少万吨？（结果精确到0.1 ）

20．（8 分）小颖为学校联欢会设计了一个“配紫色”的游戏；下面是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，游戏者同时转动两个转盘，如果转盘 A 转出了红色，转盘 B 转出了蓝色，那么他就赢了，因为红色和蓝色在一起配成了紫色．（1）利用树状图或列表的方法表示出游戏所有可能出现的结果；（2）游戏者获胜的概率是多少？ A 盘 B 盘 21．（10 分）云南 2009 年秋季以来遭遇百年一遇的全省性特大旱灾，部分坝塘干涸，小河、小溪断流，更为严重的情况是有的水库已经见底，全省库塘蓄水急剧减少，为确保城乡居民生活用水，有关部门需要对某水库的现存水量进行统计，以下是技术员在测量时的一些数据：水库大坝的横截面是梯形 ABCD （如图 7 所示）， AD ∥BC ， EF 为水面，点 E 在 DC 上，测得背水坡 AB 的长为18 米，倾角 B 30°，迎水坡CD 上线段 DE 的长为8 米， ADC 120°．（1）请你帮技术员算出水的深度（精确到 0.01 米，参考数据 3 ≈1.732 ）；（2）就水的深度而言，平均每天水位下降必须控制在多少米以内，才能保证现有水量至少能使用20 天？（精确到0.01 米）图 7

22．（11 分）在如图 8 所示的方格图中，每个小正方形的顶点称为“格点”，且每个小正方形的边长均为 1 个长度单位，以格点为顶点的图形叫做“格点图形”，根据图形解决下列问题：（1）图中格点△A B C 是由格点△ABC 通过怎样变换得到的？（2）如果建立直角坐标系后，点 A 的坐标为（ 5 ， 2 ），点 B 的坐标为( 5，0) ，请求出过 A 点的正比例函数的解析式，并写出图中格点△DEF 各顶点的坐标．图 8 23．（14 分）如图 9，已知直线l 的解析式为 y x 6 ，它与 x 轴、y 轴分别相交于 A 、B两点，平行于直线l 的直线n 从原点O 出发，沿 x 轴正方向以每秒1个单位长度的速度运动，运动时间为t 秒，运动过程中始终保持n∥l ，直线n 与 x 轴， y 轴分别相交于 C 、D 两点，线段CD 的中点为 P ，以 P 为圆心，以CD 为直径在CD 上方作半圆，半圆面积为 S ，当直线 n 与直线l 重合时，运动结束．（1）求 A 、 B 两点的坐标；（2）求 S 与t 的函数关系式及自变量t 的取值范围；（3）直线n 在运动过程中， ① 当 t 为何值时，半圆与直线l 相切？ ② 是否存在这样的t 值，使得半圆面积 S 若不存在，说明理由． 1 2 S梯形ABCD ？若存在，求出t 值，第 6 页共 11 页图 9（1）图 9（2）备用图

数学答案一、选择题： 1．Ｄ 2．Ｂ 3．Ａ 4．Ｃ 5．Ｄ 6．Ｂ 7．Ｄ二、填空题： 8． 3 9． 2 10． ab(3a 4) 11． 4.6 12． x ≤6 13． 5 14． 25 15．15 三、解答题： 16. 解： x 3 2 x 9 2x 4 x 3 · 2x x 2 2 4 x x 2 9 x 3 · x 2 2(x 2) (x 3)(x 3) 1 2(x 3) ···································· ···································· ····························5 分当 x 5 时，原式 1 1 2( 5 3) 4 ························· ························· ···············7 分 17. 解：（1） △AOB ≌△COD 、 △AOD ≌△COB、 △ABD ≌△CDB、 △ADC ≌△CBA································································································································4 分（2）以△AOB ≌△COD 为例证明，四边形 ABCD 是平行四边形， OA OC，OB OD ．在 △AOB 和 △COD 中， OA OC， AOB COD， OB OD．   △AOB ≌△COD ································ 共 11 页

资料库

2010年云南昭通中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料