logo资料库

matlabFFT小波变换-基于Mallat算法和快速傅里叶变换的电能质量分析方法.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.32M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    第 31 卷 第 19 期 2007 年 10 月 文章编号：1000-3673（2007）19-0035-06 中图分类号：TM933 文献标识码：A 学科代码：470·4051 Power System Technology 电 网 技 术 Vol. 31 No. 19 Oct. 2007 基于 Mallat 算法和快速傅里叶变换 的电能质量分析方法 张 斌 1，孙 静 2 （1．陕西省电力公司调度中心，陕西省 西安市 710048； 2．北京航空航天大学 自动化科学与电气工程学院，北京市 海淀区 100083） A Power Quality Analysis Method Based on Mallat Algorithm and Fast Fourier Transform ZHANG Bin1，SUN Jing2 （1．Dispatching Center of Shaanxi Electric Power Corporation，Xi’an 710048，Shaanxi Province，China；2．School of Automation Science and Electrical Engineering，Beijing University of Aeronautics and Astronautics，Haidian District，Beijing 100083，China） to ABSTRACT: Based on Mallat algorithm and fast Fourier transform (FFT), the authors propose a power quality analysis method. In this method, the wavelet denoising is applied to sampled signals; according the detection results of catastrophe point of signals, the high frequency coefficients of the first level and the second level obtained by Mallat decomposition algorithm are taken as the criteria to distinguish steady state disturbance from non-steady state disturbance, and then the duration of disturbance can be solved. In the light of frequency band division principle of multi-resolution analysis, by use of Mallat reconstruction algorithm the transient disturbance waveform is extracted, moreover an identification subroutine that can accurately distinguish short-term variation disturbances such as voltage sag, voltage swell and interruption is programmed. For steady state disturbance, the authors point out that FFT can be used as a tool to distinguish harmonics from flicker. The effectiveness and accuracy of the proposed method is validated by Matlab-based simulation results. KEY WORDS: power quality；Mallat algorithm；fast Fourier transform (FFT)；wavelet denoising 摘要：提出了一种基于 Mallat 算法和快速傅里叶变换的电能 质量分析方法。将小波消噪应用于采样信号，根据信号的突 变点检测结果，将采用 Mallat 分解算法得到的第一层和第二 层高频系数作为区分稳态和非稳态扰动的判据，进而求出扰 动的持续时间。根据多分辨分析的频带划分原理，采用 Mallat 重构算法提取出了暂态扰动波形，并编制了可准确判别电压 骤降、骤升和断电等短期变化扰动的识别子程序。对于稳态 扰动，提出可将快速傅里叶变换作为区分谐波和闪变的一种 手段。Matlab 的仿真结果验证了该方法的准确性和有效性。 关键词：电能质量；Mallat 算法；快速傅里叶变换(FFT)； 小波消噪 0 引言 随着电能质量问题的日益严重和用户对电能 质量要求的不断提高，建立电能质量监测与分析系 统，对电能质量扰动进行正确地检测、评估和分类 十分必要[1-2]。近年来，广泛应用于电能质量分析领 域的方法有傅里叶变换法(fast Fourier transform， FFT)[3]、小波变换法[4]、S 变换法[5-6]、希尔伯特– 黄变换法[7]和基于数学形态学的方法[8-9]等。 电力系统的电磁扰动现象非常庞杂[10]，要对其类 型进行正确地识别绝非易事。傅里叶变换已被证明非 常适用于进行谐波分析，但因其不具有时域分析能 力，所以在分析含有短时高频分量和长时低频分量的 信号时有很大的局限性。由于具有良好的时–频局部 化特性，小波变换可以聚焦到信号的任意细节，能够 很好地处理突变信号，因此特别适于分析非稳态的畸 变波形[11]。自从 Ribeiro 最早将小波变换引入电能质 量分析领域后[12]，国内外许多学者都利用小波变换研 究电能质量问题，虽然小波变换可以克服傅里叶变换 的局限性，但其自身也有不足之处，如利用小波变换 不能准确地测量谐波分量的幅值[13]。 针对上述问题，本文将傅里叶变换和小波变换 结合起 来进 行电能 质量 扰动的 检测 与分类 ：以 Mallat 分解算法得到的第一层和第二层高频系数为 区分稳态扰动和非稳态扰动的判据，进而确定扰动
    36 张斌等：基于 Mallat 算法和快速傅里叶变换的电能质量分析方法 Vol. 31 No.19 的持续时间；根据多分辨分析的频带划分原理，利 用 Mallat 重构算法提取暂态扰动波形；编制可准确 判别电压骤降、骤升和断电等短期变化扰动的识别 子程序，以进一步区分短期变化扰动的类型。 1 信号的采样和消噪 本文分析的电能质量扰动是基频 ff 为 60 Hz 且 经规格化处理后的信号，即电压幅值为标幺值。设 每个周期的采样点数 N=128，则采样频率 fs=Nff= 128×60=7680 Hz。这样选定采样频率有 2 个好处： ①根据耐奎斯特采样定理，用 FFT 进行谐波分析可 以得到的最高谐波次数，即 h=N/2–1=128/2–1=63 次， 完全能够满足电力系统谐波分析的要求；②采样频率 为 7680 Hz 时，其硬件系统设计相对简单，构建硬件 系统所需的成本也不高。 对于频率成分较高的振荡暂态和脉冲暂态，需 采用采样频率为几兆赫兹[14]的信号进行分析，但这 样会使成本过高且数据过多，不利于进行在线分 析。由于这类高频扰动并非电能质量监测和分析的 重点，考虑到硬件系统的设计及其成本问题，本文 将扰动信号的采样频率取为 7680 Hz。同理，若分 析对象是基频 ff 为 50 Hz 的扰动信号，仍取 N=128， 则对应的采样频率 fs= Nff =128×50=6400Hz。 实际的电能质量信号可能包含高频突变部分和 噪声。电能质量分析的必要前提是对采集到的电能 质量信号进行有效地去噪处理，并保留突变点的信 息[15]。小波变换的自适应性使其能够有效地区分信 号中的突变部分和噪声，从而对信号消噪[16]。本文 将 Daubechies 4 小波(简称为 D4 小波)分解为 3 层， 并采用史坦的无偏似然估计(Stein’s unbiased risk estimate，SURE)原理对小波系数进行阈值量化，然 后对信号进行重构，从而达到消噪的目的。 2 基于 Mallat 算法和 FFT 的电能质量分析 方法 2.1 多分辨分析和小波函数 1988 年 S.Mallat 在构造正交小波基时提出了多 分辨分析(multi resolution analysis，MRA)的概念， 给出了正交小波的构造方法和正交小波变换的快 速算法，即 Mallat 算法[11]。本文主要基于该算法进 行扰动持续时间的检测和扰动波形的提取。 在多分辨分析中，尺度函数的双尺度方程和小 波函数的双尺度方程[11]可分别表示为 φ t ( ) = 2 h k t ( ) (2 φ − k ) (1) Ψ t ( ) = 2 g k t ( ) (2 φ − k ) (2) ∞ ∑ −∞ ∞ ∑ −∞ 从式(1)(2)可以看出，小波基 ( )tΨ 可由尺度函 数 ( )tφ 经平移和伸缩后的线性组合构成，其构造过 程实际上就是低通滤波器 H(ω)(h(k)的频域表示形 式)和带通滤波器 G(ω)(g(k)的频域表示形式)的设计 过程。由于 Mallat 算法不需要知道尺度函数 )(tφ 和 小波函数 ( )tΨ 的具体结构，仅根据滤波器系数即可 实现对信号的快速分解与重构，因此 Mallat 算法也 称为快速小波变换(fast wavelet transform，FWT)。 采用 Mallat 算法对信号进行分解和重构时，常 用的滤波器为 Daubechies 滤波器。由于滤波器长度 系数为 4 的 D4 小波很适于进行电能质量分析[17]， 因此本文选择 D4 小波作为 Mallat 算法的母小波。 2.2 分解层数 为检测和提取电能质量扰动信号，必须确定合 理的分解层数并正确划分信号的频带。频带划分的 原则如下：尽量使信号的基频 ff 位于最低子频带的 中心，以限制基频分量对其它子频带的影响。扰动 信号的采样频率为 fs 时，Mallat 算法的实际频带划 分数目 pZ 可由下式向最近的整数取整获得： p = log [ 2 f s /( 8 )] 0.5 + f f 式中：p 为理论频带划分数目； s / 8 带的中心频率。 f (3) 为最高子频 本文分析的电能质量信号的基频为 60 Hz，采 样频率为 7680 Hz。由式(3)求得的实际子频带数目 pZ=6，即应对信号进行 5 层多分辨分析，因此其频 带范围依次为 0~120 Hz、120~240 Hz、240~480 Hz、 480~960 Hz、960~1920 Hz 和 1920~3840 Hz。当系 统频率在 60 Hz 左右波动时，基频会落在最低子频 带 0~120 Hz 的中心附近。 2.3 信号突变点 利用小波变换检测信号突变点的方法如下：对 信号进行多尺度分析，由于信号出现突变时，其经 小波变换后的系数具有模极大值，因此根据检测到 的模极大值点可以确定扰动发生的时刻。一般根据 多分辨分析得到的第一层和第二层高频系数确定 突变点的位置，从而得到扰动发生的时刻。本文用 DDn 和 ADn 分别表示小波分解后第 n 层的高频系数 和低频系数，用 DRn 和 ARn 分别表示小波重构后 第 n 层的高频系数和低频系数，其中下标 D 和 R
    第 31 卷 第 19 期 电 网 技 术 37 分别表示小波分解和小波重构。 进行信号的突变点检测时，必须考虑数据窗的 大小。为保证检测方法的实用性和实时性，在仿真时 分别将数据窗分为 8 个周期(1024 个采样点)和 4 个周 期(512 个采样点)。模极大值的检测步骤如下： （1）对数据窗内的采样序列进行小波分解， 得到第一层高频系数 DD1 和第二层高频系数 DD2。 （2）求 DD1 和 DD2 的模平均值(所有系数绝对 值的平均值)，记为 Mmean。 （3）求出 DD1 和 DD2 的模最大值(所有系数绝 对值中的最大值)，记为 Mmax。 （4）比较模最大值与模平均值，若(Mmax− Mmean)/Mmean 大于设定的阈值，则认为已检测到突变 点；否则认为没有检测到突变点。需要指出，上述 的阈值往往随因素变化而变化，因此根据仿真情 况，本文将阈值设在 10 左右。 （5）若检测到突变点，则记下突变发生的时 刻并进一步进行小波分解和重构；若没有检测到突 变点，则将其视为稳态信号。 （6）数据窗右移 1/4 个周期(32 个采样点)，重 复上述步骤。 由仿真结果可知：对于电压骤降、电压骤升、 断电、振荡暂态和脉冲暂态等非稳态扰动，其 DD1、 DD2、DR1 和 DR2 有明显的模极大值，可根据检测出 的模极大值点来确定扰动发生和终止的时刻，即扰 动的持续时间；对于谐波和闪变等稳态扰动以及纯 正弦波电压，其 DD1、DD2、DR1 和 DR2 没有明显的 模极大值。因此可根据 DD1、DD2、DR1 和 DR2 提供 的信息区分上述 2 类信号。 2.4 扰动持续时间和扰动波形 如果在 DD1 和 DD2 中检测到了模极大值点，则 说明信号有突变点，对应的电能质量扰动属非稳态 扰动。另外，检测出 DD1 和 DD2 的模极大值点即可 方便地得出扰动的持续时间。 由文献[10]可知，非稳态扰动主要包括暂态扰 动、短期变化扰动和长期变化扰动 3 类。为进一步 区分上述 3 种扰动，可将扰动持续时间作为划分扰 动的依据。短期电压变化的持续时间为 0.5 个周期 到 1min；长期电压变化的持续时间大于 1min；而 暂态扰动的持续时间却具有不确定性，一次脉冲暂 态也许只有几纳秒，而一次低频振荡暂态则可能持 续数十毫秒。因此根据扰动持续时间可以较好地区 分短期和长期变化扰动，但如果低频振荡暂态的持 续时间恰好位于短期变化扰动对应的持续时间范 围内，上述判据就失去了效力。 为解决这一问题，本文采用 Mallat 重构算法提 取出暂态扰动波形。设扰动持续时间为 ∆T，通过 对 f=1/∆T 所在的频带进行重构即可提取出扰动的 波形。利用重构的扰动波形提供的信息(如暂态扰动 的幅值和上升沿等)即可对扰动作进一步分类。为提 取出更精确的扰动波形，还有必要对 f=1/∆T 所在频 带的相邻子频带进行小波重构，这是因为左、右相 邻子频带也或多或少地包含扰动的信息，且扰动频 率也不一定落在其相应子频带的中心。因此可对上 述 3 个子频带进行小波重构，并将其小波重构系数 相加，根据傅里叶变换的叠加性质可知，相加后的 信号可完全表征原始信号的频域特征。重构得出的 扰动波形可作为人工神经元网络(artificial neural network ， ANN) 或 模 糊 专 家 系 统 (fuzzy expert system，FES)的输入信号，从而进行离线的扰动识 别和评估。 对大量暂态扰动进行仿真的结果表明：该方法 对低、中频振荡暂态的提取效果较好，但受采样频 率的限制，该方法不能用来提取频率成分过高的振 荡暂态。另外，由于短期变化扰动的持续时间通常 远大于暂态过程的持续时间，其频谱成分大都集中 在最低子频带，易造成频谱混叠，无法区分基波和 扰动波形，因此上述方法对短期变化扰动的提取效 果并不理想。 综上所述，为正确区分暂态扰动、短期变化扰 动和长期变化扰动，必须先用 Mallat 分解算法确定 扰动的持续时间，再用 Mallat 重构算法提取扰动波 形，然后将二者结合起来作为对非稳态扰动进行分 类的依据。 2.5 短期变化扰动 在确定某个非稳态现象属于短期变化扰动之 后，需进一步判断扰动类型，即区分断电、电压骤 降和电压骤升。根据这 3 种扰动的定义，本文编制 的短期变化扰动识别子程序如图 1 所示，其中 U 为 ∆T 时段内的电压有效值。由于长期变化扰动的进 一步分类方法在原理上与短期变化扰动的分类原 理相同，因此其分类识别程序可以此类推。 2.6 稳态现象 如果 DD1 和 DD2 中没有模极大值点，则说明信 号没有突变点，对应的电能质量现象可能为稳态扰 动或正常情况。由于谐波和闪变的傅里叶频谱具有
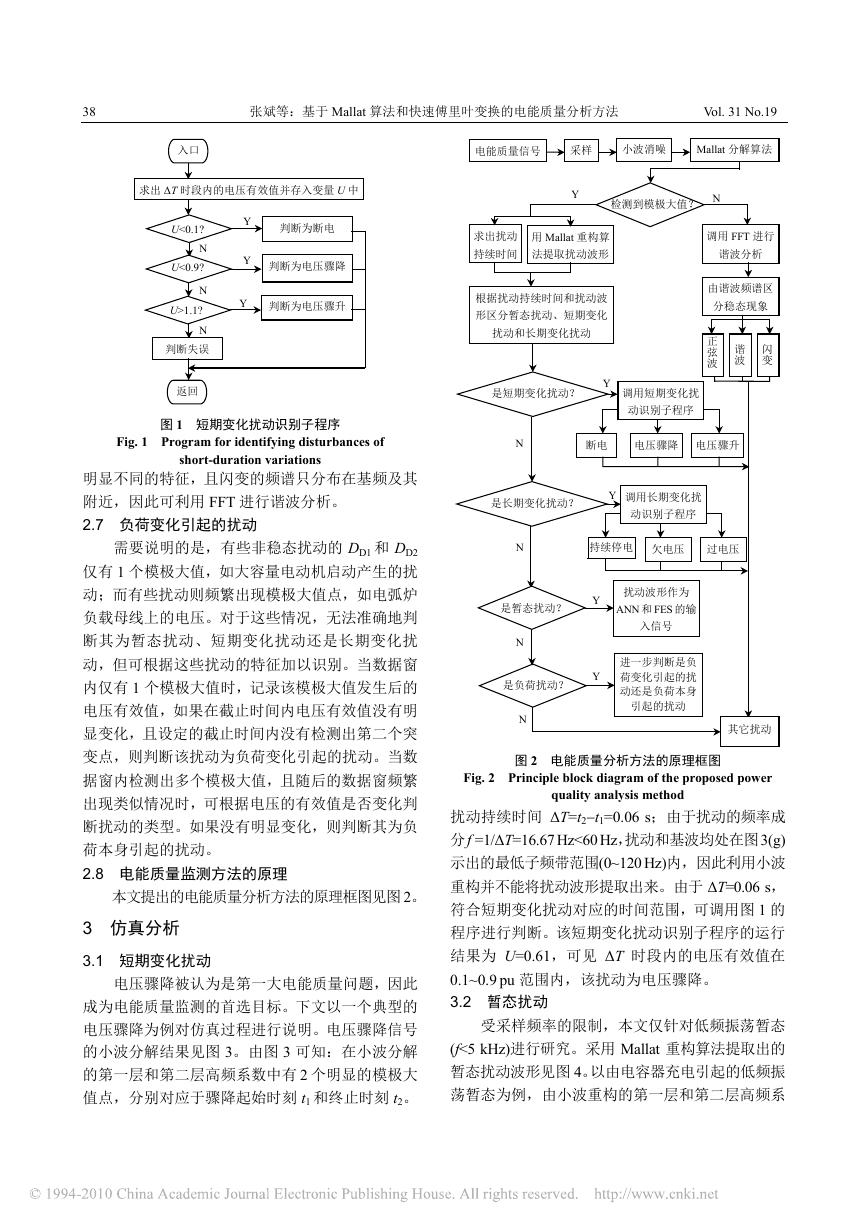
    38 张斌等：基于 Mallat 算法和快速傅里叶变换的电能质量分析方法 Vol. 31 No.19 入口 电能质量信号 采样 小波消噪 Mallat 分解算法 求出 ∆T 时段内的电压有效值并存入变量 U 中 Y 检测到模极大值？ N 断其为暂态扰动、短期变化扰动还是长期变化扰 N Y Y 判断为断电 判断为电压骤降 Y 判断为电压骤升 U<0.1? N U<0.9? N U>1.1? N 判断失误 返回 图 1 短期变化扰动识别子程序 Fig. 1 Program for identifying disturbances of short-duration variations 明显不同的特征，且闪变的频谱只分布在基频及其 附近，因此可利用 FFT 进行谐波分析。 2.7 负荷变化引起的扰动 需要说明的是，有些非稳态扰动的 DD1 和 DD2 仅有 1 个模极大值，如大容量电动机启动产生的扰 动；而有些扰动则频繁出现模极大值点，如电弧炉 负载母线上的电压。对于这些情况，无法准确地判 动，但可根据这些扰动的特征加以识别。当数据窗 内仅有 1 个模极大值时，记录该模极大值发生后的 电压有效值，如果在截止时间内电压有效值没有明 显变化，且设定的截止时间内没有检测出第二个突 变点，则判断该扰动为负荷变化引起的扰动。当数 据窗内检测出多个模极大值，且随后的数据窗频繁 出现类似情况时，可根据电压的有效值是否变化判 断扰动的类型。如果没有明显变化，则判断其为负 荷本身引起的扰动。 2.8 电能质量监测方法的原理 本文提出的电能质量分析方法的原理框图见图 2。 3 仿真分析 3.1 短期变化扰动 电压骤降被认为是第一大电能质量问题，因此 成为电能质量监测的首选目标。下文以一个典型的 电压骤降为例对仿真过程进行说明。电压骤降信号 的小波分解结果见图 3。由图 3 可知：在小波分解 的第一层和第二层高频系数中有 2 个明显的模极大 值点，分别对应于骤降起始时刻 t1 和终止时刻 t2。 求出扰动 持续时间 用 Mallat 重构算 法提取扰动波形 根据扰动持续时间和扰动波 形区分暂态扰动、短期变化 扰动和长期变化扰动 调用 FFT 进行 谐波分析 由谐波频谱区 分稳态现象 正 弦 波 谐 波 闪 变 是短期变化扰动？ Y 调用短期变化扰 动识别子程序 N 断电 电压骤降 电压骤升 是长期变化扰动？ Y 调用长期变化扰 动识别子程序 N 持续停电 欠电压 过电压 是暂态扰动？ 是负荷扰动？ N Y Y 扰动波形作为 ANN 和 FES 的输 入信号 进一步判断是负 荷变化引起的扰 动还是负荷本身 引起的扰动 其它扰动 图 2 电能质量分析方法的原理框图 Fig. 2 Principle block diagram of the proposed power quality analysis method 扰动持续时间 ∆T=t2−t1=0.06 s；由于扰动的频率成 分f =1/∆T=16.67 Hz<60 Hz，扰动和基波均处在图3(g) 示出的最低子频带范围(0~120 Hz)内，因此利用小波 重构并不能将扰动波形提取出来。由于 ∆T=0.06 s， 符合短期变化扰动对应的时间范围，可调用图 1 的 程序进行判断。该短期变化扰动识别子程序的运行 结果为 U=0.61，可见 ∆T 时段内的电压有效值在 0.1~0.9 pu 范围内，该扰动为电压骤降。 3.2 暂态扰动 受采样频率的限制，本文仅针对低频振荡暂态 (f<5 kHz)进行研究。采用 Mallat 重构算法提取出的 暂态扰动波形见图 4。以由电容器充电引起的低频振 荡暂态为例，由小波重构的第一层和第二层高频系
    电 网 技 术 u/V 2 0 −2 0 第 31 卷 第 19 期 u/V 1 0 −1 0 u/V 0.05 0 −0.05 0 u/V 0.05 0 −0.05 0 u/V 0.1 0 −0.1 0 u/V 0.5 0 −0.5 0 u/V 1 0 −1 0 u/V 10 0 −10 0 0.02 0.04 0.06 0.08 (a) 原始信号 0.02 0.02 0.02 0.02 0.02 0.02 0.04 0.06 0.08 (b) 第一层高频系数 0.04 0.06 0.08 (c) 第二层高频系数 0.04 0.06 0.08 (d) 第三层高频系数 0.04 0.06 0.08 (e) 第四层高频系数 0.04 0.06 0.08 (f) 第五层高频系数 0.04 0.06 0.08 (g) 第五层低频系数 t/s 0.12 0.1 t/s 0.12 0.1 t/s 0.12 0.1 t/s 0.12 0.1 t/s 0.12 0.1 t/s 0.12 0.1 t/s 0.12 0.1 图 3 电压骤降信号的小波分解结果 Fig. 3 Wavelet decomposition results of voltage sag 数可知，该扰动属非稳态扰动，然而由于暂态扰动 的持续时间通常远小于短期变化扰动的持续时间，因 此其模极大值特性明显不同于短期变化扰动的特征。 低频振荡暂态的衰减时间常数一般为几毫秒，如该扰 动在 DD1 中检测到的持续时间(近似值)∆T=2 ms，则 f=1/∆T=500 Hz ， 其 所 在 的 子 频 带 范 围 为 480~ 960Hz，相邻的子频带范围分别为 240~480 Hz 和 960~1920Hz。为提取出较精确的扰动波形，可将小 波重构的第二、三、四层高频系数相加，从而获得 频率范围为 240~1920 Hz 的扰动波形。 4 结论 （1）本文采用 Mallat 算法不仅获得了短期变 化扰动信号的持续时间，而且提取出了暂态扰动的 波形，为离线的扰动辨识和评估提供了依据。 （2）本文编制的短期变化的扰动识别子程序 可准确判别电压骤降、电压骤升和断电 3 种扰动。 0.02 0.04 (a) 原始信号 39 t/s 0.06 t/s 0.02 0.04 0.06 (b) 第一层高频系数 0.02 0.04 (c) 第二层高频系数 t/s 0.06 0.02 0.04 (d) 第三层高频系数 0.02 0.04 (e) 第四层高频系数 0.06 0.06 0.02 0.04 (f) 第五层高频系数 0.06 0.02 0.04 0.06 (g) 第五层低频系数 t/s t/s t/s t/s t/s 0.02 0.04 0.06 u/V 0.5 0 −0.5 0 u/V 0.5 0 −0.5 0 u/V 1 0 −1 0 u/V 0.5 0 −0.5 0 u/V 0.2 0 −0.2 0 u/V 1 0 −1 0 u/V 1 0 −1 0 (h) 第二、三、四层高频系数之和 图 4 采用 Mallat 重构算法提取出的暂态扰动波形 Fig. 4 Extracted transient disturbance waveforms by Mallat reconstruction algorithm （3）FFT 可作为区分谐波和闪变的一种手段。 参考文献 [1] 赵霞，赵成勇，贾秀芳，等．基于可变权重的电能质量模糊综合 评价[J]．电网技术，2005，29(6)：11-16． Zhao Xia，Zhao Chengyong，Jia Xiufang，et al．Fuzzy synthesis evaluation for power quality based on changeable synthesis weight [J]．Power System Technology，2005，29(6)：11-16(in Chinese)． [2] 黄攀，姚建刚，鲁栗，等．基于 WebGIS 的电能质量监测系统设 计及应用[J]．电网技术，2005，29(7)：52-55． Huang Pan，Yao Jiangang，Lu Li，et al．Design of WebGIS based power quality monitoring system and its application[J] ． Power System Technology，2005，29(7)：52-55(in Chinese)． [3] Gu J C，Yu S L．Removal of DC offset in current and voltage signals
    40 张斌等：基于 Mallat 算法和快速傅里叶变换的电能质量分析方法 Vol. 31 No.19 using a novel Fourier filter algorithm[J]．IEEE Trans on Power Delivery，2000，15(1)：73-79． [4] 刘安定，肖先勇，邓武军．基于离散余弦变换和小波变换的电能 质量扰动信号检测方法[J]．电网技术，2005，29(10)：70-74． Liu Anding，Xiao Xianyong，Deng Wujun．Detection and analysis of power quality disturbance signal based on discrete cosine transform and wavelet transform[J]．Power System Technology，2005，29(10)： 70-74(in Chinese)． [5] 刘守亮，肖先勇，杨洪耕．基于 S 变换模时频矩阵相似度的短时 电能质量扰动分类[J]．电网技术，2006，30(5)：67-71． Liu Shouliang，Xiao Xianyong，Yang Honggeng．Classification of short duration power quality disturbance based on module time-frequency matrixes similarity by S-transform[J]．Power System Technology，2006，30(5)：67-71(in Chinese)． [6] 赵凤展，杨仁刚．基于 S 变换和时域分析的电能质量扰动识别 [J]．电网技术，2006，30(15)：90-100． Zhao Fengzhan ， Yang Rengang ． Power quality disturbances classification based on S-transform and time domain analysis [J]．Power System Technology，2006，30(15)：90-100(in Chinese)． [7] 李天云，赵妍，李楠，等．基于 HHT 的电能质量检测新方法[J]．中 国电机工程学报，2005，25(17)：52-56． Li Tianyun，Zhao Yan，Li Nan，et al．A new method for power quality detection based on HHT[J]．Proceedings of the CSEE，2005，25(17)： 52-56(in Chinese)． [8] 曾纪勇，丁洪发，段献忠．基于数学形态学的谐波检测与电能质 量扰动定位方法[J]．中国电机工程学报，2005，25(21)：57-62． Zeng Jiyong，Ding Hongfa，Duan Xianzhong．Harmonics detection and disturbance location methods based on mathematical morphology[J]．Proceedings of the CSEE，2005，25(21)：57-62(in Chinese)． [9] 李庚银，罗艳，周明，等．基于数学形态学和网格分形的电能质 量扰动检测及定位[J]．中国电机工程学报，2006，26(3)：25-30． Li Gengyin，Luo Yan，Zhou Ming，et al．Power quality disturbance detection and location based on mathematical morphology and grille fractal[J]．Proceedings of the CSEE，2006，26(3)：25-30(in Chinese)． （上接第 34 页 continued form page 34） [11] 朱志斌，张可村．不等式约束优化一个新的 SQP 算法[J]．计算数 学，2004，26(4)：413-426． Zhu Zhibin，Zhang Kecun．A new SQP algorithm for inequality constrained optimization[J]．Mathmatica Numerica Sinica，2004， 26(4)：413-426(in Chinese)． [12] 薛毅．求解 Minimax 优化问题的 SQP 方法[J]．系统科学与数学， 2002，22(3)：355-364． Xue Yi．The sequential quadratic programming method for solving minimax problem[J] ． Journal of Systematic Science and Mathematics，2002，22(3)：355-364(in Chinese)． [13] 毕兆东，王建全，韩祯祥．逐步二次规划法在约束潮流中的运用 [J]．电网技术，2003，27(2)：30-33． Bi Zhaodong，Wang Jianquan，Han Zhenxiang．Constrained load flow calculation by sequential quadratic programming method[J]．Power System Technology，2003，27(2)：30-33(in Chinese)． [现代数学手册]编纂委员会．现代数学手册-经济数学卷[M]．武汉： [14] [10] Dugan R C，McGranaghan M F，Beaty H W．Electrical power systems quality[M]．New York：McGraw-Hill，1996． [11] Chui C K．An introduction to wavelets[M]．New York：Academic Press，1992． [12] Ribeiro P F．Wavelet transform: an advanced tool for analyzing non-stationary systems [C]．International Conference on Harmonics in Power Systems， Bologna，Italy，1994． distortions harmonic in power [13] Possion O，Rioual P，Meunier M．New signal processing tools applied to power quality analysis[J]．IEEE Trans on Power Delivery， 1999，14(2)：561-566． [14] Santoso S，Powers E J，Grady W M．Power quality disturbance data compression using wavelet transform methods[J]．IEEE Trans on Power Delivery，1997，12(3)：1250-1255． [15] 唐良瑞，祁兵，杨雪，等．一种基于高斯滤波器的电能质量信号 去噪算法[J]．中国电机工程学报，2006，26(10)：18-22． Tang Liangrui，Qi Bing，Yang Xue，et al．A de-noising method of power quality signal based on Gaussian filter[J]．Proceedings of the CSEE，2006，26(10)：18-22(in Chinese)． [16] 薛蕙，杨仁刚．基于小波包除噪的电能质量扰动检测方法[J]．中 国电机工程学报，2004，24(3)：85-90． Xue Hui，Yang Rengang．Power quality disturbance detection method using wavelet package transform based de-noising scheme [J]．Proceedings of the CSEE，2004，24(3)：85-90(in Chinese)． [17] Brito N S D，Souza B A，Pires F A C．Daubechies wavelets in quality of electrical power[C]．International Conference on Harmonics and Quality of Power，Athens，Greece，1998：511-515． 收稿日期：2007-08-06。 作者简介： 张 斌(1976—)，男，硕士，工程师，主要从事电网调度、电能质 量分析和电压无功控制的研究工作，E-mail：zhangbin@snepc.com； 孙 静(1975—)，女，博士，主要从事混杂电力系统的综合集成 建模与智能优化控制、电力系统稳定性分析方面的研究工作。 （编辑 杜宁） [15] 华中科技大学出版社，1999． [运筹学]教材编写组．运筹学(第三版)[M]．北京：清华大学出版 社，2005． [16] 刁勤华，默哈默德·夏班，倪以信．运用连续二次规划法计算区域 间极限传输容量[J]．电力系统自动化，2000，16(24)：5-8． Diao Qinhua，Mohamed Shaaban，Ni Yixin．Inter-area total transfer capability calculation using sequential quadratic programming method in power market[J]．Automation of Electric Power Systems， 2000，16(24)：5-8(in Chinese)． 收稿日期：2007-03-12。 作者简介： 刘崇茹(1977—)，女，博士，讲师，主要从事交直流混合电力系 统分析与仿真、运行与控制、IEC61970 系列标准制定等方面的科研和 教学工作，E-mail：chongru.liu@ncepu.edu.cn。 （责任编辑 马晓华）
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料