自适应模糊神经控制系统及其 MATLAB 实现 摘 要：本文介绍了自适应神经模糊网络控制系统的结构，并在此基础上重点介绍了自适应神经模糊系统 及其 MATLAB 实现。 关键词：自适应；神经模糊系统；MATLAB Abstract： This text has introduced the structure of the fuzzy network control system of adaptive nerve ，and has recommended especially fuzzy system and MATLAB of the adaptive nerve are realized on this basis. Key woeds: adaptive;neuro_fuzzy system;MATLAB 1 引言 模糊神经网络控制在控制领域里目前已经成为一个研究的热点，其原因在于神经网络和模糊系统两者 之间的互补关系。尽管模糊推理系统的设计（隶属度函数和模糊规则的建立）不主要依靠对象的模型，但是它 却相当依靠专家或操作人员的经验和知识。若缺乏这样的经验和知识，则很难期望它能获得满意的控制效果。 而神经网络的一大特点就是其自学习功能，将这种自学习的方法应用于对模型特征的分析与建模上，产生自适 应的神经网络技术。这种自适应的神经网络技术对于模糊系统的模型建立（模糊规则库的建立）是非常有效的 工具。而自适应神经模糊系统就是基于数据的建模方法，该系统中的模糊隶属度函数及模糊规则是通过大量的 已知数据的学习得到的，而不是基于经验和直觉任意给定的，这对于那些特性还不被人们所完全了解或者特性 非常复杂的系统尤为重要。 2 自适应神经模糊网络控制系统的结构 自适应神经模糊网络系统的定义是指具有学习算法的神经模糊网络系统，这里的神经模糊网络系统是 由服从模糊逻辑规则的一系列“如果—则”规则所构造的；而学习算法则依靠数据信息来对神经模糊系统的参 数进行调整。自适应模糊神经系统被认为是通过学习能自动产生模糊规则的神经模糊网络系统。神经模糊网络 控制系统的结构图如图 1 所示。其中 NFNC 为神经模糊网络控制器；R 为输入信号；E、EC 分别为误差及误差变 化量化后的模糊量；Ke、Kc 为量化因子。 图 1 自适应神经模糊网络控制系统结构图 因此可以说神经模糊网络是具有自适应性的, 并能够根据被控对象和环境的变化来调整控制规则和控 制器的参数。 

3 模糊推理系统生成方式 （1）在 MATLAB 模糊逻辑工具箱中，提供了有关对自适应神经模糊推理系统的初始化和建模函数，如 表 1 所示。 表 1 模糊神经系统函数 函数名 功能 genfis1( ) anfis ( ) 采用网格分割方式生成模糊推理函数 自适应神经模糊系统的建模函数 （2）采用网格分割方式生成模糊推理系统 函数 genfis1( )可为训练自适应神经模糊推理系统（Adaptive Neuro-Fuzzy Inference System, 简称 ANFIS）产生 Takagi-Sugeno 型模糊推理系统（Fuzzy Inference System,简称 FIS）结构的初值（隶属度 函数参数的初值），它采用网格分割的方式，根据给定数据集生成一个模糊推理系统，一般与函数 anfis ( ) 配合使用。由 genfis1( )生成的模糊推理系统的输入和隶属度函数的类型、数目可以在使用时指定，也可以 采用默认值。该函数的调用格式为 fisMat=genfisl(data) fisMat= genfisl(data,numMFs,inMFType,outMFType) 其中，data 为给定的输入/输出数据集合，除了一系列为输出数据外，其余列均表示输入数据；numMFs 为一向量，其各个分量用于指定每个输入语言变量的隶属度函数的数量，如果每个输入的隶属度函数的数量相 同，则只需输入标量值；inMFType 为一字符串阵列，其每一列指定一个输入变量的隶属度类型，如果类型相 同，则该参数将变成一个一维的字符串；outMFType 指定输出隶属度类型的字符串，由于只能采用 Takagi-Sugeno 型系统，因此系统只能有一个输出，其类型仅取 linear 或 constant;fisMat 为生成的模糊推 理系统矩阵。当仅使用一个输入参数而不指定隶属度函数的个数和类型时，将使用默认值，即输入隶属度函数 个数为 2，输入隶属度函数类型为钟形（gbellmf）曲线，输出隶属度函数为线行（linear）曲线。 我们可以利用函数 genfis1( )产生一个两输入—单输出的模糊推理系统。其中要求输入隶属度函数分 别为π形（pimf）和三角形（trimf）,分割数分别为 5 和 7。编程 MATLAB 为： data=[rand(10,1) 10*rand(10,1)-5 rand(10,1)]; numMFs = [5 7]; imfType=str2mat('pimf','trimf'); omfType=str2mat('linear'); fisMat=genfis1(data,numMFs,imfType,omfType);％生成模糊推理系统 subplot(2,1,1);plotmf(fisMat,'input',1); subplot(2,1,2);plotmf(fisMat,'input',2); 根据以上 MATLAB 程序，可以得到由函数 genfis1( )生成的 ANFIS 系统训练前的初始隶属度函数曲 线，如图 2 所示。 

图 2 由函数 genfis1( )生成的隶属度函数曲线 由图 2 可以看出，根据函数 genfis1( )生成的模糊推理系统的输入/输出隶属度函数的曲线，在确保 覆盖整个输入/输出空间的基础上对其进行了均匀分割。 （3）自适应神经模糊系统的建模 在 MATLAB 模糊逻辑工具箱中，提供了对基于 Takagi-Sugeno 型模型的自适应神经模糊推理系统 ANFIS 的建模方法，该模糊推理系统利用 BP 反向传播算法和最小二乘算法来完成对输入/输出数据对的建模。该系统 为模糊建模的过程，提供了一种能够从数据集中提取相应信息（模糊规则）的学习方法。这种学习方法与神经 网络的学习方法非常相似，通过学习能够有效的计算出隶属度函数的最佳参数，使得设计出来的 Takagi-Sugeno 型模糊推理系统能够最好地模拟出希望的或是实际的输入/输出关系。相应的函数为 anfis(), 该函数的输出为一个三维或五维向量。当未指定检验数据时，输出向量为三维。Anfis（）支持采用输出加权 平均的一阶或零阶 Takagi-Sugeno 型模糊推理。该函数的调用格式为 [ Fis,error,stepsize ]=anfis (trnData) [ Fis,error,stepsize ]=anfis (trnData,initFis) [ Fis,error,stepsize ]=anfis (trnData,initFis,trnOpt,disOpt) [ Fis,error,stepsize,chFis,chkEr ]=anfis (trnData,initFis,trnOpt,disOpt.chkData) [ Fis,error,stepsize,chFis,chkEr ]=anfis (trnData,initFis,trnOpt,disOpt.chkData,optMethod) 其中， 1） trnData 为训练学习的输入/输出数据矩阵，该矩阵的每一行对应一组输入/输出数据，其中最 后一列为输出数据（该函数仅支持单输出的 Takagi-Sugeno 型模糊系统）； 2） initFis 是指定初始的模糊推理参数（包括隶属度函数的类型和参数）的矩阵，该矩阵可以使 用命令 fuzzy 通过模糊推理系统编辑器生成，也可使用函数 genfisl()由训练数据直接生成。函数 genfisl() 的功能是采用网格分割法生成模糊推理系统。如果没有指明该参数，则函数 anfis()会自动调用 genfisl()来 按照输入/输出数据生成一个默认初始 FIS 推理系统参数。这里使用函数 genfisl()的作用是先根据一定的专 

家经验给出一个初始模糊系统的合适结构，在使用函数 anfis()的训练过程中，已经给定的初始模糊系统的结 构（隶属度函数的个数、模糊规则数目）不会改变，只是对相应的结构参数进行调整和优化； 3） trnOpt 指定训练的有关选项，参数 trnOpt 为一个五维向量，其各个分量的定义如下：trnOpt （1）为训练的次数，默认值为 10；trnOpt（2）为期望误差，默认值是 0；trnOpt（3）为初始步长，默认值 是 0.01；trnOpt（4）为步长递减速率，默认值是 0.9；trnOpt（5）为步长递增速率，默认值为 1.1。如果 trnOpt 的任一个分量为 NaN（非数值，IEEE 的标准缩写）或被省略，则训练采用默认参数。学习训练的过程在参数得 到指定值或训练误差得到期望误差时停止。训练过程中的步长调整采用以下的策略：当误差连续四次减小时， 则增加步长；当误差变化连续两次出现震荡，即一次增加和一次减少交替发生时，则减小步长。trnOpt 的第 四个和第五个参数分别按照上述策略控制训练步长的调整； 4） disOpt 用于控制训练过程中 MATLAB 命令窗口的显示内容，参数 disOpt 为一个四维向量，各分 量分别定义如下： disOpt（1）显示 ANFIS 的信息，如输入/输出隶属度函数的次数，默认值为 1；disOpt（2）显示 误差测量，默认值为 1； disOpt（3）显示训练步长，默认值为 1；disOpt（4）显示最终结果，默认值为 1。当 disOpt 的 一个分量为 0 时不显示相应内容，如果为 1 或 NaN 或省略则显示相应内容； 5） chkData 参数为一个与训练数据矩阵有相同列数的矩阵，用于提供检验数据，当提供检验数据 时，anfis（）返回对检验数据具有最小均方根误差的模糊推理系统 chkFis; 6） optMethod 为隶属度函数参数训练中的可选最优化方法，其中 1 表示混合方法（BP 算法和最小 二乘法的组合），0 表示 BP 方法，默认值为 1； 返回参数 Fis 为学习完成后得到的对应训练数据具有最小均方根误差的模糊推理系统矩阵； 7） error 为训练数据对应的最小根误差向量； 8） stepsize 为训练步长向量（当指定检验数据后，输出向量为五维参数向量）； 9） chkFis 为对检验数据具有最小均方根误差的模糊推理系统； 10) chkEr 为检验数据对应的最小均方根误差。 利用 anfis（）函数进行自适应模糊系统建模，除了给定系统期望的输入/输出数据之外，还必须提供 一个初始模糊推理系统（包括隶属度函数的类型和参数），否则函数 anfis（）会自动调用 genfisl（）来按 照输入/输出数据生成一个默认的系统。我们对于这样一个非线性函数 ， 建立一个自适 应神经模糊推理系统，对其进行逼近。编写 MATLAB 程序如下： X=0:0.1:10;y=sin(2*x)./exp(x/5);trnData=[x'y'];%训练学习的输入/输出数据 numMFs =5;mfType='gbellmf'; initFis= genfis1(trnData,numMFs, mfType); epoch_n=30; fisMat=anfis(trnData, initFis, epoch_n); 

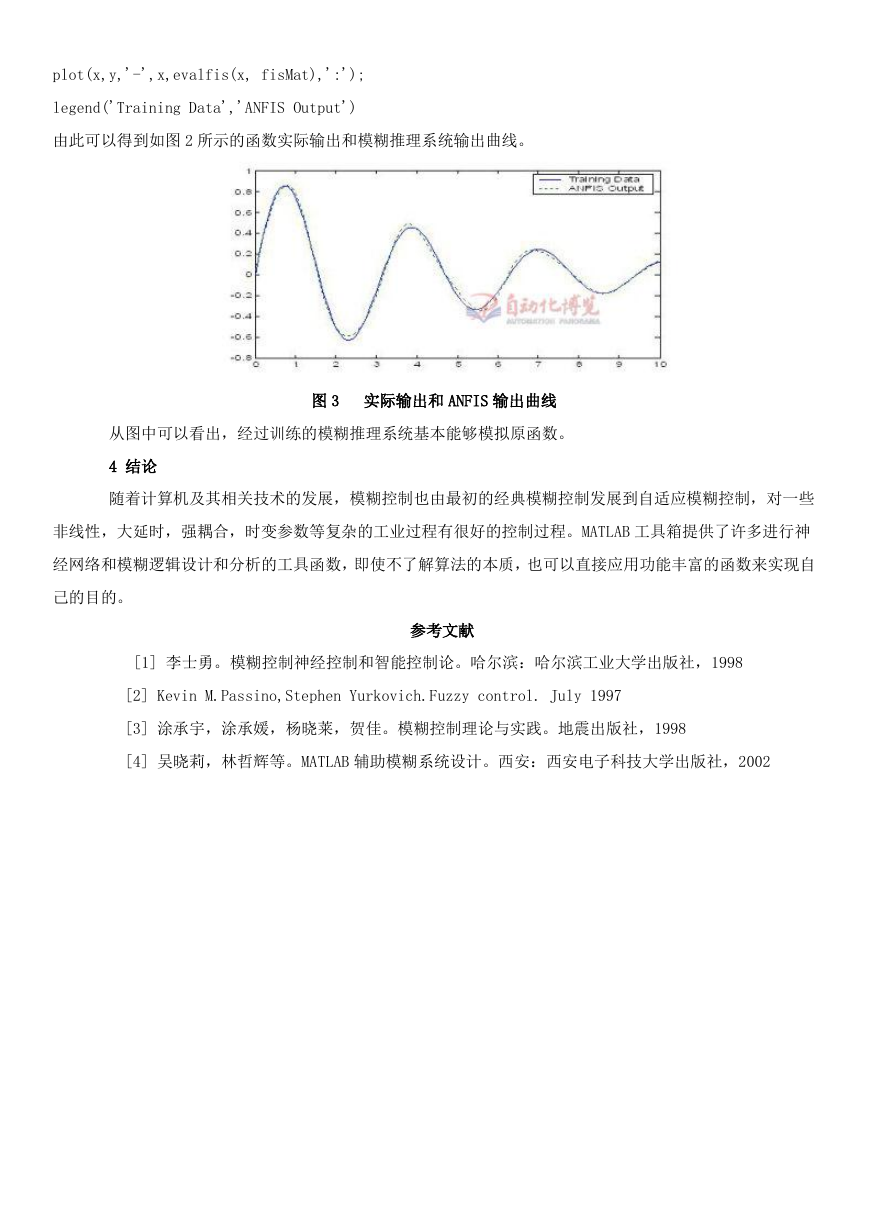
plot(x,y,'-',x,evalfis(x, fisMat),':'); legend('Training Data','ANFIS Output') 由此可以得到如图 2 所示的函数实际输出和模糊推理系统输出曲线。 图 3 实际输出和 ANFIS 输出曲线 从图中可以看出，经过训练的模糊推理系统基本能够模拟原函数。 4 结论 随着计算机及其相关技术的发展，模糊控制也由最初的经典模糊控制发展到自适应模糊控制，对一些 非线性，大延时，强耦合，时变参数等复杂的工业过程有很好的控制过程。MATLAB 工具箱提供了许多进行神 经网络和模糊逻辑设计和分析的工具函数，即使不了解算法的本质，也可以直接应用功能丰富的函数来实现自 己的目的。 参考文献 [1] 李士勇。模糊控制神经控制和智能控制论。哈尔滨：哈尔滨工业大学出版社，1998 [2] Kevin M.Passino,Stephen Yurkovich.Fuzzy control. July 1997 [3] 涂承宇，涂承媛，杨晓莱，贺佳。模糊控制理论与实践。地震出版社，1998 [4] 吴晓莉，林哲辉等。MATLAB 辅助模糊系统设计。西安：西安电子科技大学出版社，2002