Matlab解微分方程(ODE+PDE).pdf

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：0.56M 资料格式：pdf 举报版权申诉

wangguopo1-9341777-4744300845133353830.pdf-第1页.png

第1页 / 共33页

wangguopo1-9341777-4744300845133353830.pdf-第2页.png

第2页 / 共33页

wangguopo1-9341777-4744300845133353830.pdf-第3页.png

第3页 / 共33页

wangguopo1-9341777-4744300845133353830.pdf-第4页.png

第4页 / 共33页

wangguopo1-9341777-4744300845133353830.pdf-第5页.png

第5页 / 共33页

wangguopo1-9341777-4744300845133353830.pdf-第6页.png

第6页 / 共33页

wangguopo1-9341777-4744300845133353830.pdf-第7页.png

第7页 / 共33页

wangguopo1-9341777-4744300845133353830.pdf-第8页.png

第8页 / 共33页

文本预览

常微分方程： 1 ODE 解算器简介(ode**) 2 微分方程转换 3 刚性/非刚性问题(Stiff/Nonstiff) 4 隐式微分方程(IDE) 5 微分代数方程(DAE) 6 延迟微分方程(DDE) 7 边值问题(BVP) 偏微分方程(PDEs)Matlab 解法偏微分方程： 1 一般偏微分方程组(PDEs)的命令行求解 2 特殊偏微分方程(PDEs)的 PDEtool 求解 3 陆君安《偏微分方程的 MATLAB 解法先来认识下常微分方程(ODE)初值问题解算器(solver) [T,Y,TE,YE,IE] = odesolver(odefun,tspan,y0,options) sxint = deval(sol,xint) Matlab 中提供了以下解算器：输入参数： odefun：微分方程的 Matlab 语言描述函数，必须是函数句柄或者字符串，必须写成 Matlab

规范格式(也就是一阶显示微分方程组)，这个具体在后面讲解 tspan=[t0 tf]或者[t0,t1,…tf]：微分变量的范围，两者都是根据 t0 和 tf 的值自动选择步长，只是前者返回所有计算点的微分值，而后者只返回指定的点的微分值，一定要注意对于后者 tspan 必须严格单调，还有就是两者数据存储时使用的内存不同(明显前者多)，其它没有任何本质的区别 y0=[y(0),y’(0),y’’(0)…]：微分方程初值，依次输入所有状态变量的初值，什么是状态变量在后面有介绍 options：微分优化参数，是一个结构体，使用 odeset 可以设置具体参数，详细内容查看帮助输出参数： T：时间列向量，也就是 ode**计算微分方程的值的点 Y：二维数组，第 i 列表示第 i 个状态变量的值，行数与 T 一致在求解 ODE 时，我们还会用到 deval()函数，deval 的作用就是通过结构体 solution 计算 t 对应 x 值，和 polyval 之类的很相似！参数格式如下： sol：就是上次调用 ode**函数得道的结构体解 xint：需要计算的点，可以是标量或者向量，但是必须在 tspan 范围内该函数的好处就是如果我想知道 t=t0 时的 y 值，不需要重新使用 ode 计算，而直接使用上次计算的得道 solution 就可以 [教程] 微分方程转换为一阶显示微分方程组方法好，上面我们把 Matlab 中的常微分方程(ODE)的解算器讲解的差不多了，下面我们就具体开始介绍如何使用上面的知识吧！现实总是残酷的，要得到就必须先付出，不可能所有的 ODE 一拿来就可以直接使用，因此，在使用 ODE 解算器之前，我们需要做的第一步，也是最重要的一步，借助状态变量将微分

方程组化成 Matlab 可接受的标准形式(一阶显示常微分方程)！如果 ODEs 由一个或多个高阶微分方程给出，则我们应先将其变换成一阶显式常微分方程组！下面我们以两个高阶微分方程构成的 ODEs 为例介绍如何将之变换成一个一阶显式常微分方程组。 step1.将微分方程的最高阶变量移到等式的左边，其他移到右边，并按阶次从低到高排列，假如说两个高阶微分方程最后能够显式的表达成如下所示：我们说过现实总是残酷的，有时方程偏偏是隐式的，没法写成上面的样子，不用担心 Matlab 早就为我们想到了，这个留在后面的隐式微分方程数值求解中再详细讲解！ step2.为每一阶微分式选择状态变量，最高阶除外从上面的变换，我们注意到，ODEs 中所有因变量的最高阶次之和就是需要的状态变量的个数，最高阶的微分式(比如上面的 x (m)和 y(n))不需要给它一个状态变量 step3.根据上面选用的状态变量，写出所有状态变量的一阶微分的表达式

注意到，最高阶次的微分式的表达式直接就是 step1 中的微分方程好，到此为止，一阶显式常微分方程组，变化顺利结束，接下来就是 Matlab 编程了。请记住上面的变化很重要，Matla 中所有微分方程的求解都需要上面的变换。下面通过一个实例演示 ODEs 的转换和求解【解】真是万幸，该 ODEs 已经帮我们完成了 step1，我们只需要完成 step2 和 step3 了 (1)选择一组状态变量 (2)写出所有状态变量的一阶微分表达式

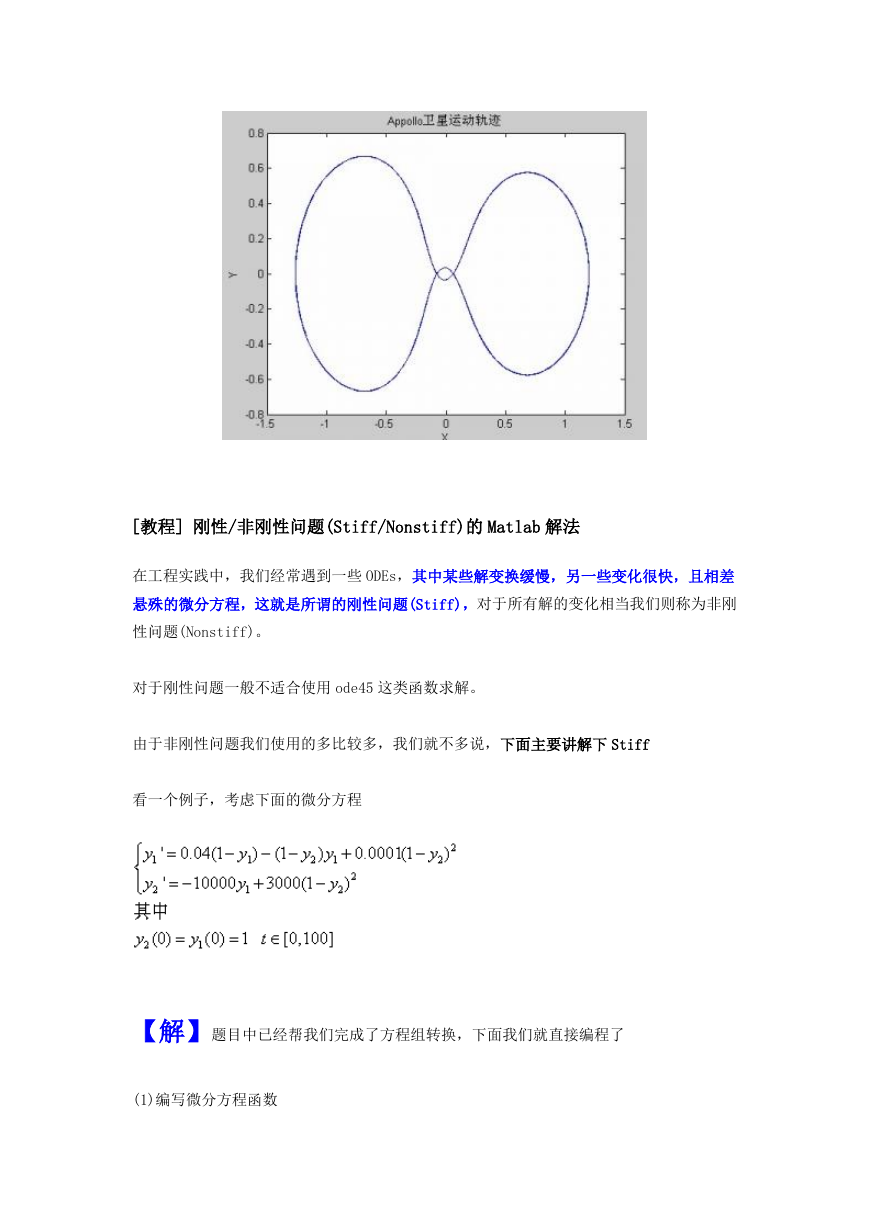
(4)有了数学模型描述，则可以立即写出相应的 Matlab 代码了(这里我们优先选择 ode45) 1. 2. x0=[1.2;0;0;-1.04935751];%x0(i)对应与 xi 的初值 options=odeset('reltol',1e-8);%该命令的另一种写法是 options=odeset;options.reltol=1e-8; 3. tic 4. [t,y]=ode45(@appollo,[0,20],x0,options);%t 是时间点，y 的第 i 列对应 xi 的值，t 和 y 的行数相同 5. toc 6. 7. 8. 9. plot(y(:,1),y(:,3))%绘制 x1 和 x3，也就是 x 和 y 的图形 title('Appollo 卫星运动轨迹') xlabel('X') ylabel('Y') 10. 11. function dx=appollo(t,x) 12. mu=1/82.45; 13. mustar=1-mu; 14. r1=sqrt((x(1)+mu)^2+x(3)^2); 15. r2=sqrt((x(1)-mustar)^2+x(3)^2); 16. dx=[x(2) 17. 2*x(4)+x(1)-mustar*(x(1)+mu)/r1^3-mu*(x(1)-mustar)/r2^3 18. x(4) 19. -2*x(2)+x(3)-mustar*x(3)/r1^3-mu*x(3)/r2^3];

[教程] 刚性/非刚性问题(Stiff/Nonstiff)的 Matlab 解法在工程实践中，我们经常遇到一些 ODEs，其中某些解变换缓慢，另一些变化很快，且相差悬殊的微分方程，这就是所谓的刚性问题(Stiff)，对于所有解的变化相当我们则称为非刚性问题(Nonstiff)。对于刚性问题一般不适合使用 ode45 这类函数求解。由于非刚性问题我们使用的多比较多，我们就不多说，下面主要讲解下 Stiff 看一个例子，考虑下面的微分方程【解】题目中已经帮我们完成了方程组转换，下面我们就直接编程了 (1)编写微分方程函数

1. 2. 3. 4. 5. odefun=@(t,x)[0.04*(1-x(1))-(1-x(2))*x(1)+0.0001*(1-x(2))^2 -1e4*x(1)+3000*(1-x(2))^2]; x0=[0 1]; tspan=[0 100]; options=odeset('reltol',1e-6,'abstol',1e-8); (2)对于这个刚性问题，我们先使用 ode45 函数试试(反正我们是没有信心等待它，太慢了) 1. 2. tic;[t,y]=ode45(odefun,tspan,x0,options);toc disp(['ode45 计算的点数' num2str(length(t))]) (3)换用 ode15s 函数试试看看 1. 2. tic;[t2,y2]=ode15s(odefun,tspan,x0,options);toc disp(['ode15s 计算的点数' num2str(length(t2))]) (4)绘图看看结果 1. 2. 3. 4. 5. 6. 7. figure('numbertitle','off','name','Stiff ODEs Demo—by Matlabsky') subplot(121) title('Using ode45') plot(t,y) subplot(122) plot(t2,y2) title('Using ode15s') 运行的结果如下，我们可以比较下 ode45 和 ode15s 的差距 1. 2. 3. 4. Elapsed time is 171.005688 seconds. ode45 计算的点数 356981 Elapsed time is 0.397287 seconds. ode15s 计算的点数 188

[教程] 隐式微分方程(IDE)的 Matlab 解法上帝不会总是那么仁慈的，不是所有的 ODEs 都是可以直接显式的表达成下面的样子比如，下面的隐式微分方程组那该如何办呢？在这里我们介绍三种解决方法，但是前两者是技巧方法，没有使用 Mathworks 专为 IDE 开发的 ode15i 函数：

分享到：

赞收藏

资料库

Matlab解微分方程(ODE+PDE).pdf

相关推荐

课程资源

热门标签

最新资料