2021-2022学年甘肃省临洮县八年级上学期期中数学试题及答案.doc-资料库

2021-2022学年甘肃省临洮县八年级上学期期中数学试题及答案.doc.pdf-第1页.jpg

第1页 / 共7页

2021-2022学年甘肃省临洮县八年级上学期期中数学试题及答案.doc.pdf-第2页.jpg

第2页 / 共7页

2021-2022学年甘肃省临洮县八年级上学期期中数学试题及答案.doc.pdf-第3页.jpg

第3页 / 共7页

2021-2022学年甘肃省临洮县八年级上学期期中数学试题及答案.doc.pdf-第4页.jpg

第4页 / 共7页

2021-2022学年甘肃省临洮县八年级上学期期中数学试题及答案.doc.pdf-第5页.jpg

第5页 / 共7页

2021-2022学年甘肃省临洮县八年级上学期期中数学试题及答案.doc.pdf-第6页.jpg

第6页 / 共7页

2021-2022学年甘肃省临洮县八年级上学期期中数学试题及答案.doc.pdf-第7页.jpg

第7页 / 共7页

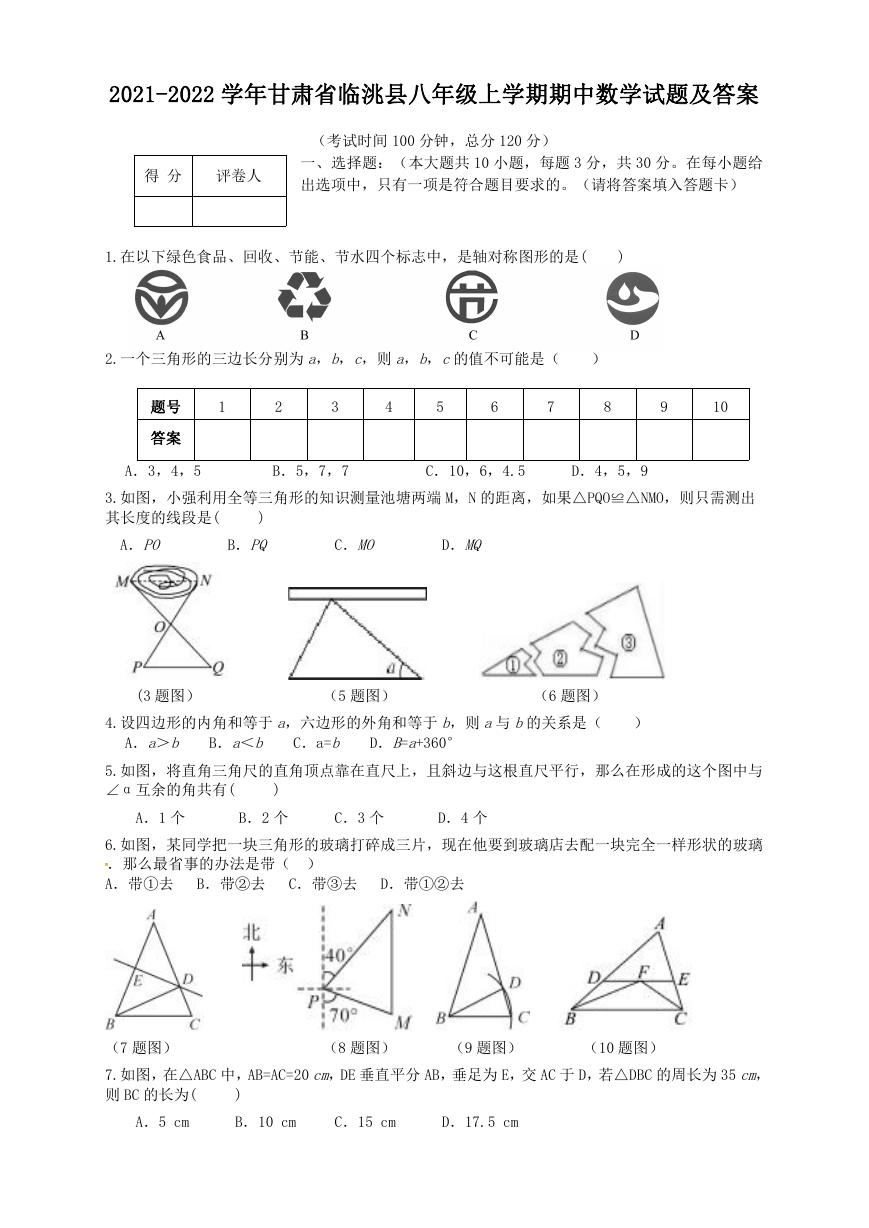
2021-2022 学年甘肃省临洮县八年级上学期期中数学试题及答案（考试时间 100 分钟，总分 120 分）得分评卷人一、选择题：（本大题共 10 小题，每题 3 分，共 30 分。在每小题给出选项中，只有一项是符合题目要求的。（请将答案填入答题卡） 1.在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是( ) 2.一个三角形的三边长分别为 a，b，c，则 a，b，c的值不可能是（） 1 2 3 4 5 6 7 8 9 10 题号答案 A．3，4，5 B．5，7，7 C．10，6，4.5 D．4，5，9 3.如图，小强利用全等三角形的知识测量池塘两端 M，N 的距离，如果△PQO≌△NMO，则只需测出其长度的线段是( ) A．PO B．PQ C．MO D．MQ (3 题图）（5 题图）（6 题图） 4.设四边形的内角和等于 a，六边形的外角和等于 b，则 a与 b的关系是（） A．a＞b B．a＜b C．a=b D．B=a+360° 5.如图，将直角三角尺的直角顶点靠在直尺上，且斜边与这根直尺平行，那么在形成的这个图中与 ∠α互余的角共有( ) A．1 个 B．2 个 C．3 个 D．4 个 6.如图，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块完全一样形状的玻璃．那么最省事的办法是带（） A．带①去 B．带②去 C．带③去 D．带①②去（7 题图）（8 题图）（9 题图）（10 题图） 7.如图，在△ABC 中，AB=AC=20 cm，DE 垂直平分 AB，垂足为 E，交 AC 于 D，若△DBC 的周长为 35 cm，则 BC 的长为( ) A．5 cm B．10 cm C．15 cm D．17.5 cm

8.如图，一艘海轮位于灯塔 P 的南偏东 70°方向的 M 处，它以每小时 40 海里的速度向正北方向航行，2 小时后到达位于灯塔 P 的北偏东 40°的 N 处，则 N 处与灯塔 P 的距离为( ) A．40 海里 B．60 海里 C．70 海里 D．80 海里 9.如图，在△ABC 中，AB=AC，∠A=30°，以 B 为圆心，BC 的长为半径画弧，交 AC 于点 D，连接 BD，则∠ABD=( ) A．30° B．45° C．60° D．90° 10.如图，∠ABC，∠ACB 的平分线相交于点 F，过点 F 作 DE∥BC，交 AB 于 D，交 AC 于 E，那么下列结论正确的是：①△BDF，△CEF 都是等腰三角形；②DE=BD＋CE；③△ADE 的周长为 AB＋AC；④ BD=CE.( ) A．③④ B．①②③ C．①② D．②③④ 二、填空题（本大题共 8 小题，每小题 3 分，共 24 分。）得分评卷人 11．一木工师傅现有两根木条，木条的长分别为 40 cm和 30 cm，他要选择第三根木条，将它们钉成一个三角形木架．设第三根木条长为 x cm，则 x 的取值范围是． 12.点 P（1，﹣2）关于 y轴对称的点的坐标为． 13．等腰三角形的周长为 14，其一边长为 4，那么它的底边为。（14 题图）（15 题图） 14.如图，正方形 ABCD中，截去∠A，∠C后，∠1，∠2，∠3，∠4 的和为． 15.如图，点 B、F、C、E在一条直线上，已知 FB=CE，AC∥DF，请你添加一个适当的条件使得△ABC≌△DEF．（16 题图）（17 题图） 16.如图，已知 PA⊥ON 于 A，PB⊥OM 于 B，且 PA=PB，∠MON=50°，∠OPC=30°，则∠PCA= . 17.如图，在 Rt△ABC 中，∠B=90°，AB=3 cm，S△ABC=6 cm2，将△ABC 折叠，使点 C 与点 A 重合，得折痕 DE，则△ABE 的周长等于 cm. 18.当三角形中一个内角α是另一个内角β的一半时，我们称此三角形为“半角三角形”，其中α 称为“半角”．如果一个“半角三角形”的“半角”为 20°，那么这个“半角三角形”的最大内角的度数为 . 三、解答题（一）（19 题 4 分，20 题 6 分，21 题 5 分，22 题 7 分，23 题 7 分，共 29 分） 19.（4 分）如图，AD⊥BC，∠1=∠B，∠C=65°，求∠BAC的度数

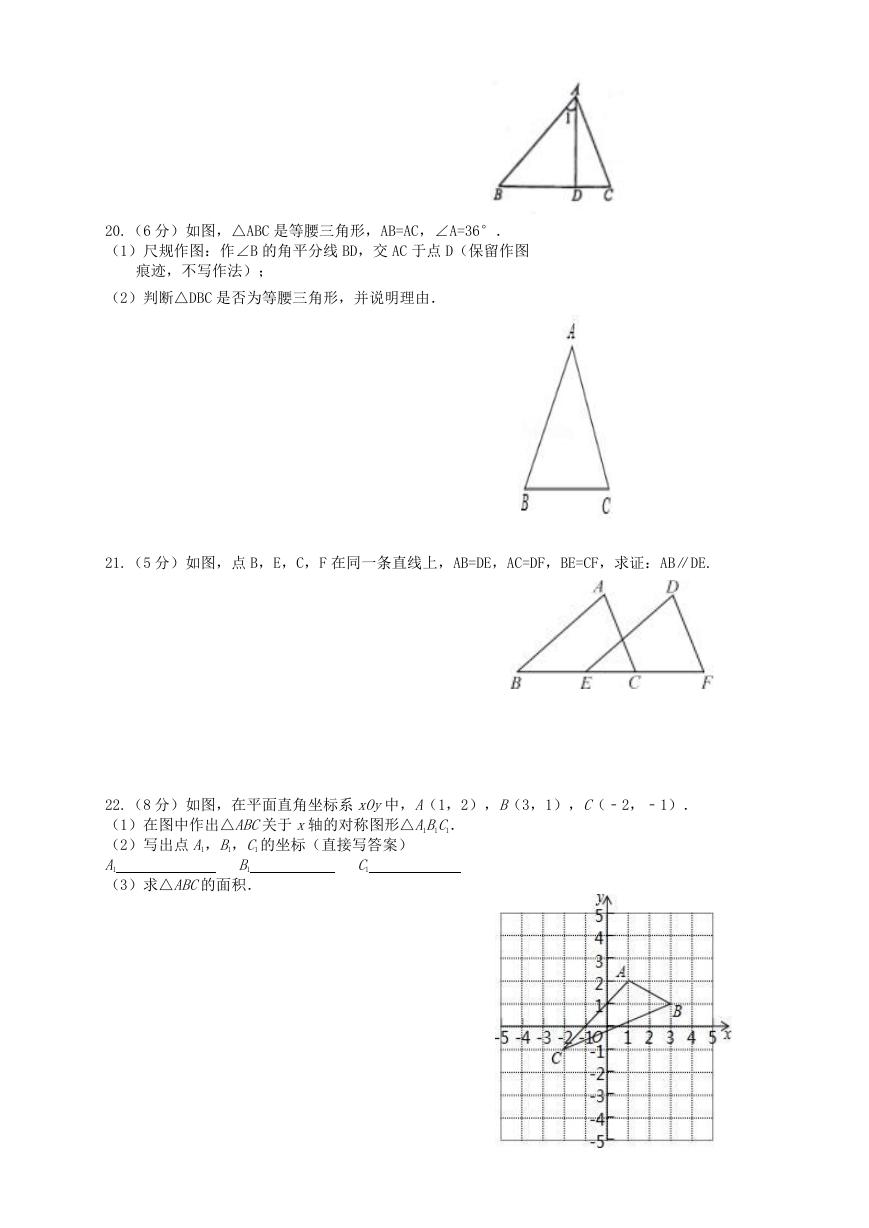
20.（6 分）如图，△ABC 是等腰三角形，AB=AC，∠A=36°．（1）尺规作图：作∠B 的角平分线 BD，交 AC 于点 D（保留作图痕迹，不写作法）；（2）判断△DBC 是否为等腰三角形，并说明理由． 21.（5 分）如图，点 B，E，C，F 在同一条直线上，AB=DE，AC=DF，BE=CF，求证：AB∥DE. 22.（8 分）如图，在平面直角坐标系 xOy中，A（1，2），B（3，1），C（﹣2，﹣1）．（1）在图中作出△ABC关于 x轴的对称图形△A1B1C1．（2）写出点 A1，B1，C1 的坐标（直接写答案） A1 （3）求△ABC的面积． B1 C1

23.（7 分）如图，在△ABC 中, ∠ACB=90°,AC=BC,直线 MN 经过点 C, 点 E, 求证：（1）△ADC≌△CEB；（2）DE=AD+BE AD⊥MN 于点 D, BE ⊥MN 于四、解答题（二）（24、25 每小题各 6 分，26 题 8 分，27 题 8 分、28 题 9 分，共 37 分） 24.（8 分）如图点 C，E，F，B 在同一直线上，点 A，D 在 BC 异侧，AB∥CD，AE=DF，∠A=∠D. (1)求证：AB=CD；(2)若 AB=CF，∠B=30°，求∠D 的度数． 25.（8 分）如图，AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证：BD 平分 EF. 26.（10 分）如图，BD 是∠ABC 的平分线，AB＝BC，点 E 在 BD 上，连接 AE，CE，DF⊥AE，DG⊥CE，垂足分别是 F，G. (1)求证：△ABE≌△CBE；(2)求证：DF＝DG. 27.（10 分）如图，在四边形 ABCD 中，AD∥BC，E 为 CD 的中点，连接 AE、BE，BE⊥AE，延长 AE 交 BC 的延长线于点 F. 求证：(1)FC＝AD；(2)AB＝BC＋AD.

28.（9 分）AB 和 AC 相交于点 A,BD 和 CD 相交于点 D,探究∠BDC 与∠B 、 ∠C、∠BAC 的关系小明是这样做的：解：如图（2）以点 A 为端点作射线 AD ∵∠1 是△ABD 的外角 ∴∠1= ∠B+∠BAD 同理∠2=∠C+∠CAD ∴∠1+∠2=∠B+∠BAD+∠C+∠CAD 即∠BDC=∠B+∠C+∠BAC 小英的思路是：如图（3）延长 BD 交 AC 于点 E. 图（1）图（2）图（3） ⑴按小英的思路完成∠BDC=∠B+∠C+∠BAC 这一结论.(4 分) (2)（5 分）如图：△ABC 中，BO、CO 分别是∠ABC 与∠ACB 的角平分线，且 BO、CO 相交于点 O.猜想∠BOC 与∠A 有怎样的关系，并加以证明.

参考答案一、选择题： ADBCB CCDBB 二、填空题 11.10cm＜x＜70cm 15.∠A＝∠D(不唯一）三、解答题（一） 19.解：∵AD⊥BC，∴∠ADB=90°， ∵∠1+∠2+∠ADB=180°，而∠1=∠2，∴2∠2=180°-90°，∴∠2=45°， ∵∠2+∠C+∠BAC=180°，∴∠BAC=180°-45°-65°=70°． 20.（1）作图略 12.（-1，﹣2） 16.55° 13. 4 或 6 17.7 14.540° 18.120° （2）△BCD 是等腰三角形理由如下： ∵ AB="AC" , ∠A="36°" ∴∠ABC=∠C="72° ∵ BD 平分∠ABC ∴∠DBC= ∠ABC=36° ∴∠BDC=∠C="72°∴△BCD 是等腰三角形 21.证明：∵BE=CF ∴BE+EC=CF+EC ∴BC=EF 在△ABC 和△DEF 中 BC=EF AB=DE AC=DF ∴△ABC≌△DEF(SSS) ∴∠A=∠D 22.解：（1）如图，△A1B1C1 即为所求；（2）答案：A1 （1，﹣2），B1 （3，﹣1），C1 （﹣2，1）．（3）S△ABC＝5×3﹣ ×3×3﹣ ×2×1﹣ ×5×2 ＝15﹣4.5﹣1﹣5 ＝4.5． 23.（1）证明： ∵∠ACB=90°，∴∠ACD+∠BCE=90°，而 AD⊥MN 于 D，BE⊥MN 于 E， ∴∠ADC=∠CEB=90°，∠BCE+∠CBE=90°， ∴∠ACD=∠CBE．在△ADC 和△CEB 中 ∠ADC=∠CEB ∠ACD=∠CBE AC=BC ∴△ADC≌△CEB（AAS），（2）由（1）得∴△ADC≌△CEB（AAS）， ∴AD=CE，DC=BE， ∴DE=DC+CE=BE+AD；四、解答题（二） 24.(1)易证△ABE≌△DCF(AAS)，∴AB=CD

(2)∵△ABE≌△DCF，∴AB=CD，BE=CF， ∵AB=CF，∠B=30°，∴CF=CD， 1 ∴∠CFD=∠D，∴∠D= 2 ×(180°－30°)=75° 25.证明：∵AE=CF，∴AE+EF=CF+EF，即 AF=CE，在 RT△ABF 和 RT△CDE 中， AB=CD AF=CE ∴RT△ABF≌RT△CDE（HL），∴DE=BF，在△DEO 和△BFO 中， ∠EOD=∠FOB ∠DEO=∠BFO=90° DE=BF ∴△DEO≌△BFO（AAS），∴EO=FO，∴BD 平分 EF． 26. (1)易证△ABE≌△CBE(SAS) (2)由(1)得∠AEB=∠CEB，∴∠AED=∠CED，又∵DF⊥AE，DG⊥CE，∴DF=DG 27.证明：(1)∵AD∥BC∴∠ADE＝∠ECF ∵E 是 CD 的中∴DE＝EC 在△ADE 和△FCE 中 ∠ADE＝∠ECF DE＝EC ∠AED＝∠CEF ∴△ADE≌△FCE(ASA) ∴FC＝AD (2) ∵△ADE≌△FCE∴AE＝EF，AD＝CF ∵BE⊥AE∴BE 是线段 AF 的垂直平分线∴AB＝BF＝BC＋CF ∵AD＝CF∴AB＝BC＋AD 28.解：(1)证明：延长 BD 交 AC 于 E ∵∠BDC= ∠C+∠CED 又∵∠CED=∠BAC+∠B∴∠BDC=∠C+∠B+∠BAC (2). ∠BOC 与∠A 的关系：∠BOC=90°+ 1 2 ∠A(过程略）

资料库

2021-2022学年甘肃省临洮县八年级上学期期中数学试题及答案.doc

相关推荐

初中二年级

热门标签

最新资料