matlab 二维插值--interp2 与 griddata from: matlab 功能强大，以至于不知道他不能做什么，只是怨自己没有找到相应的函数。 二者均是常用的二维差值方法，两者的区别是，interp2 的插值数据必须是矩形域，即已知 数据点（x,y)组成规则的矩阵，或称之为栅格，可使用 meshgid 生成。而 griddata 函数的已 知数据点（X，Y）不要求规则排列，特别是对试验中随机没有规律采取的数据进行插值具 有很好的效果。griddata(X,Y,XI,YI,'v4') v4 是一种插值算法，没有具体的名字，原文称为 “MATLAB 4 griddata method”，是一种很圆滑的差值算法，效果很好。X 和 Y 提供的已知 数据点，XI 和 YI 是需要插值的数据点，一般使用 meshgrid 生成，当然也可以其他数据， 但是那样绘图的时候就比较麻烦，不能使用 mesh 等，只能使用 trimesh。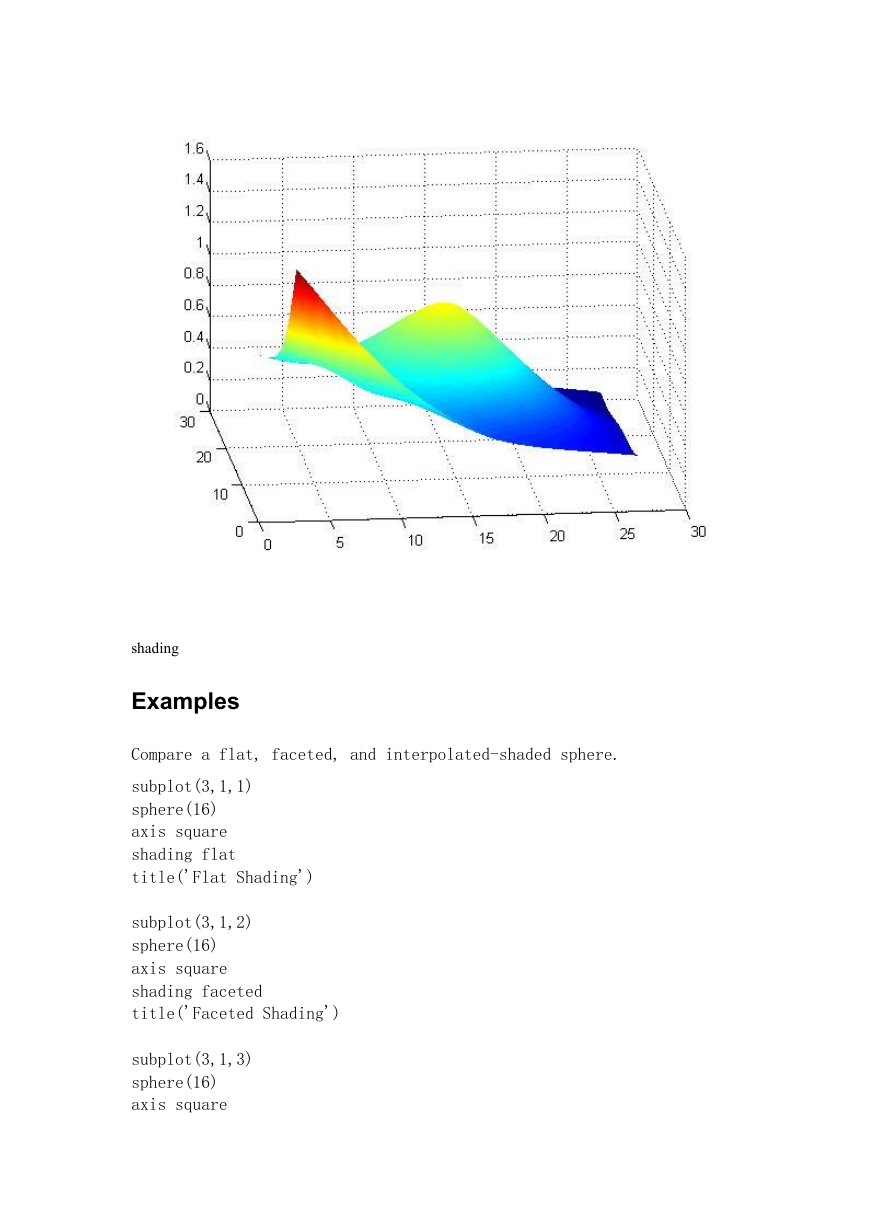 示例如下： a=[ 3 3 1.5300 3 27 0.4210 5 17 0.5980 9 9 0.5900 13 25 0.4470 15 15 1 17 5 0.3830 21 21 0.3100 25 13 0.2830 27 3 0.2820 27 27 0.1200 ]; x=a(:,1); y=a(:,2); z=a(:,3); xtemp=linspace(min(x),max(x),100); ytemp=linspace(min(y),max(y),100); [X,Y]=meshgrid(xtemp,ytemp); Z=griddata(x,y,z,X,Y,'v4'); surf(X,Y,Z) shading interp 

‍ shading Examples Compare a flat, faceted, and interpolated-shaded sphere. subplot(3,1,1) sphere(16) axis square shading flat title('Flat Shading') subplot(3,1,2) sphere(16) axis square shading faceted title('Faceted Shading') subplot(3,1,3) sphere(16) axis square 

shading interp title('Interpolated Shading')