阵列天线方向图的MATLAB实现.pdf-资料库

sinat_29606341-15350753-16359647465108942322.pdf-第1页.png

第1页 / 共6页

sinat_29606341-15350753-16359647465108942322.pdf-第2页.png

第2页 / 共6页

sinat_29606341-15350753-16359647465108942322.pdf-第3页.png

第3页 / 共6页

sinat_29606341-15350753-16359647465108942322.pdf-第4页.png

第4页 / 共6页

sinat_29606341-15350753-16359647465108942322.pdf-第5页.png

第5页 / 共6页

sinat_29606341-15350753-16359647465108942322.pdf-第6页.png

第6页 / 共6页

第 25 卷第 1 期 2010 年 6 月西藏大学学报自然科学版） ( JOURNAL OF TIBET UNIVERSITY Vol.25 No.1 Jun. 2010 阵列天线方向图的 MATLAB 实现陈天禄郭燕红（西藏大学理学院西藏拉萨 850000）摘要：天线的方向性是指电磁场辐射在空间的分布规律，文章以阵列天线的方向性因子，）为主 φ 要研究对象来分析均匀和非均匀直线阵天线的方向性讨论了阵列天线方向图中主射方向和主瓣宽度随各参数变化的特点，借助 MATLAB 绘制出天线方向性因子的二维和三维方向图，展示天线辐射场在空间的分布规律，表现辐射方向图的特点（ θ F 。关键词：阵列天线; 方向图；MATLAB 中图分类号：TN82 文献标识码：A 。文章编号：1005-5738（2010）01-103-05 前言。。。天线是发射和接收电磁波的重要的无线电设备，没有天线不同用途的天线要求其有不同的方向性，也就没有无线电通信阵列天线以其较强的方向性和较高的增益在工程实际中被广泛因此，对阵列天线方向性分析在天线理论研究中占有重要应用地位阵列天线方向性主要由方向性因子，（ θ F ）在远区场是一组复杂的函数，如果对它的认识和分析仅停留 φ 在公式中各参数的讨论上，很难理解阵列天线辐射场的空间分 MATLAB 以其卓越的数值计算能力和强大的绘图功布规律 [1] 能，近年来被广泛应用在天线的分析和设计中借助 MATLAB 可以绘制出阵列天线的二维和三维方向图，直观地从方向图中看出主射方向和主瓣宽度随各参数的变化情况，加深对阵列天线辐射场分布规律的理解，）表征，但 φ （ θ F 。。。 1 均匀直线阵方向图分析若天线阵中各个单元天线的类型和取向均相同，且以相等的间隔线的电流振幅均为 I ，相位依次滞后同一数值 α 图 1 均匀直线阵，那么，这种天线阵称为均匀直线式天线阵，如图 1 所示[2]: 排列在一条直线上且各单元天。 d 收稿日期： 201 0- 05- 1 4 第一作者简介：陈天禄（ 1 979- ），男，汉族，甘肃天祝人，西藏大学理学院讲师，主要研究方向为宇宙线和天文。 γ - 103 -

陈天禄，郭燕红：阵列天线方向图的 MATLAB 实现均匀直线阵归一化阵因子为[3]：（ θ Fn ，） = 准 ,ξ=kdcosθ-α ，（1） sin nξ 2 nsin ξ 2 （ θ ，）是一个周期函数，所以除准 =0 时是阵因子的主瓣最大值外， = ξ 2 ± ξ （ mπ m=1,2,... Fn 大值，这些重复的主瓣称为栅瓣，在实际应用中，通常希望出现一个主瓣，为避免出现栅瓣，必须把）都是主瓣最限制 ξ 在 -2 ＜ ξ π ＜2 π 范围内[4]，其中 1.1 边射式直线阵 = 2 π k λ ，即波数， n 表示阵元数目。当均匀直线阵各天线元上的电流都同相时，即 α =0 时，天线阵最大辐射方向为垂直于天线阵的轴线方向，即 = ± π2 θ 方向，这种天线阵称为边射式直线阵,其归一化阵因子为： Fn sin （ θ ndcosθ ），准 = " " 边射阵不出现栅瓣的条件是 2! 2! kdcosθ sin 1.2 普通端射式直线阵（2）＜ λ。 d 天线阵的最大辐射方向指向阵直线的方向，即射式天线阵的归一化阵因子为： =0 的方向，这样的直线阵叫做端射式直线阵，普通端 θ sin （ θ Fn ），准 = （（ ! nkd 2 ! kd 2 nsin cosθ-1 cosθ-1 "） "）（3）普通端射阵方向图不产生栅瓣的条件为 1.3 强方向式端射阵 d ＜ λ 2 2n# 1- 1 $。为了提高普通端射阵的方向性，可以通过控制单元间的电流相位差来实现即在普通端射阵的基础。上将相邻单元间的初相差加上 π n 归一化因子为：的相位延迟，这种均匀直线阵称为强方向性端射阵，强方向式端射阵的（ θ Fn ，）准 =sin π 2n# $sin sin % n 2 % 1 2 （（ ! kd ! kd cosθ-1 cosθ-1 强方向端射阵方向图不产生栅瓣的条件为 1.4 相位扫描直线阵 d ＜ λ 2 ）） " & - π （4） n " & - π n n# 1- 1 $。改变均匀直线阵相邻电流相位差连续改变单元天线之间的电流相位差，即可连续地改变天线的主射方向，这样无需转动天线，即可实现在一定范围内的方向性扫描，这种天线阵称为相控阵天线，相位扫描直线阵的归一化阵因子为：将引起方向图最大辐射方向相应地变化。 α sin （ θ Fn ），准 = cosθ-cosθm （5） "） "）（（ ! nkd 2 ! kd 2 nsin cosθ-cosθm - 104 -

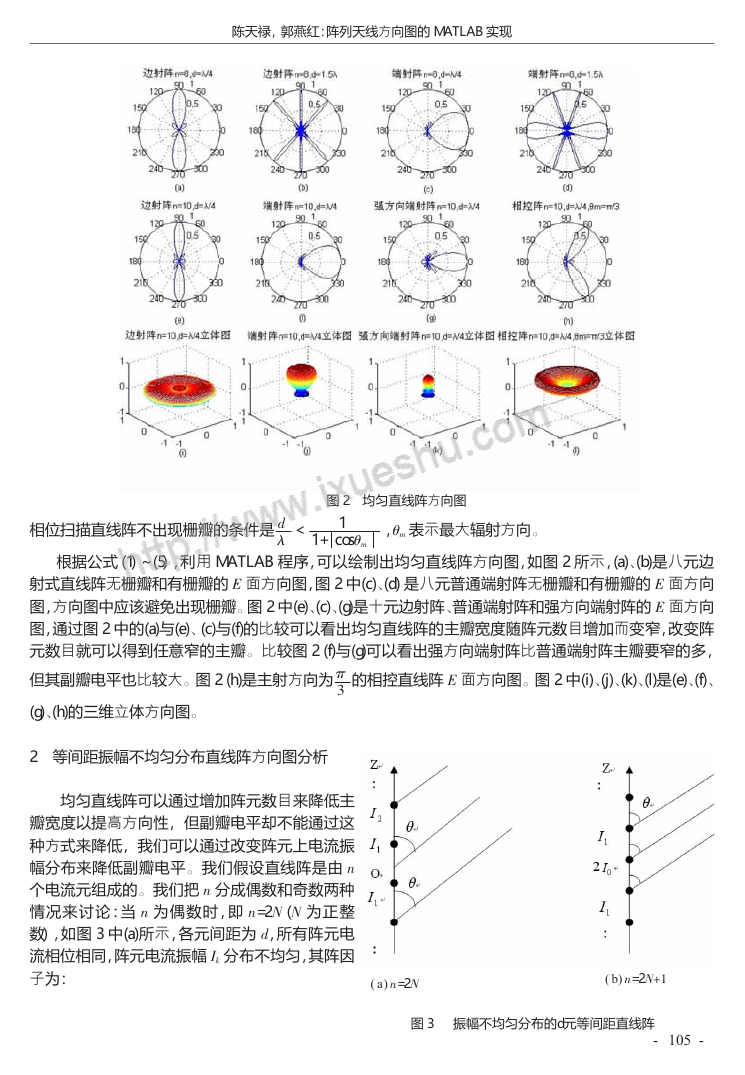
陈天禄，郭燕红：阵列天线方向图的 MATLAB 实现图 2 均匀直线阵方向图相位扫描直线阵不出现栅瓣的条件是 d λ 表示最大辐射方向， θm 。＜ 1 1+ cos θm 根据公式（1）~（5），利用 MATLAB 程序，可以绘制出均匀直线阵方向图，如图 2 所示，(a) 射式直线阵无栅瓣和有栅瓣的 E 图，方向图中应该避免出现栅瓣图，通过图 2 中的(a)与(e) 元数目就可以得到任意窄的主瓣、面方向图，图 2 中(c) 图 2 中(e) (b)是八元边、面方向 (d) 是八元普通端射阵无栅瓣和有栅瓣的、普通端射阵和强方向端射阵的面方向、 (c)与(f)的比较可以看出均匀直线阵的主瓣宽度随阵元数目增加而变窄，改变阵比较图 2 (f)与(g)可以看出强方向端射阵比普通端射阵主瓣要窄的多， (g)是十元边射阵、 (c) 、。 E E 。但其副瓣电平也比较大。 (h)的三维立体方向图、 (g) 。图 2 (h)是主射方向为 π 3 的相控直线阵面方向图 E 。图 2 中(i) (j) 、 (k) 、 (l)是(e) 、 (f) 、、 2 等间距振幅不均匀分布直线阵方向图分析均匀直线阵可以通过增加阵元数目来降低主瓣宽度以提高方向性，但副瓣电平却不能通过这种方式来降低，我们可以通过改变阵元上电流振幅分布来降低副瓣电平个电流元组成的情况来讨论：当 n 数），如图 3 中(a)所示，各元间距为流相位相同，阵元电流振幅子为： n 分成偶数和奇数两种为正整（ N N ，所有阵元电分布不均匀，其阵因。我们把为偶数时，即我们假设直线阵是由 =2 。 Ik d n n =2 N ( a) n =2 N+1 ( b) n 图 3 振幅不均匀分布的d元等间距直线阵 - 105 -

陈天禄，郭燕红：阵列天线方向图的 MATLAB 实现 N （2k-1 （ fn θ ）， = 准为奇数时，即分布不均匀，其阵因子为 Σ2Ik =2 k = 1 N 2 n 当流振幅 n Ik ） ξ ξ=kdcosθ-α （6） +1（N 为正整数），如图 3 中(b)所示，各阵元间距仍为，电流相位相同，阵元电 d （ fn θ ），准 = N Σ2Ik k = 0 （2k 2 ） ξ ξ=kdcosθ-α （7）表 1 十二元直线阵阵元电流振幅分布情况表阵元电流振幅分布 I6 (a)中心向两边递加 6 (b)均匀分布 1 I5 5 1 I4 4 1 I3 3 1 I2 2 1 I1 1 1 I1 1 1 I2 2 1 I3 3 1 I4 4 1 I5 5 1 (c)中心向两边递减 1 1.1 1.2 1.3 1.4 1.5 1.5 1.4 1.3 1.2 1.1 (d)中心向两边递减 2 4 6 8 1. 12 12 10 8 6 4 I6 6 1 1 2 (e)二项系数分布 1 11 55 165 330 462 462 330 165 55 11 1 表 1 列出了十二元直线阵阵元电流振幅分布的不同情况，根据公式（6）（7），利用 MATLAB 程序，可、由图 4 可以看出，不同的振幅分布将产以绘制出非均匀直线阵不同振幅分布的生主瓣宽度与副瓣电平都不同的方向图，图 4 (a)中振幅由中心向两边递加，其方向图副瓣最大；图 4 (b)为 (d)随着中心向两边递减幅度增大，副瓣越来越小，但均匀直线阵，其主瓣最窄，但副瓣也比较大；图 4 (c) 、主瓣越来越宽；当振幅呈二项系数分布时，由图 4 (e)可知，副瓣完全消失，但主瓣也变得最宽，而且电流振幅自阵中心向两边递减的梯度太大，给馈电带来很大的困难图 4 中 (f)是对 (d)的放大面方向图，如图 4 所示。 E 。。 - 106 - 图 4 非均匀直线阵方向图

陈天禄，郭燕红：阵列天线方向图的 MATLAB 实现从上述分析可知，使直线阵中各单元电流的振幅自阵中向两边递减，就可以降低副瓣电平以至完全消除副瓣，这样我们就可以通过调整电流振幅分布来设计出所需要的天线方向图。 3 结束语 MATLAB 辅助分析天线辐射方向图，它可以将复杂的函数以二维三维图形直观的展示出来，极大地、本文不足之处是缺少对天线方向图的定量分析，但还是。。方便了我们对阵列天线辐射场空间分布的理解体现出了 MATLAB 在天线分析和综合领域的可观前景附录：普通端射阵天线的 MATLAB 程序，对应图 2（f） clear; f=3e10; lamda=(3e8)/f; beta=2.*pi/lamda; n=10; t=0:0.01:2*pi; d=lamda/4; W=beta.*d.*cos(t); z1=((n/2).*W)-n/2*beta*d; z2=((1/2).*W)-1/2*beta*d; F1=sin(z1)./(n.*sin(z2)); K1=abs(F1); polar(t,K1); 参考文献 [1] 王曼珠.MATLAB 在天线方向图中的应用与研究[J].电气电子教学学报，2004(4). [2] 杨儒贵.电磁场与电磁波（第二版）[M].北京：高等教育出版社，2007. [3] 朱崇灿.天线[M].武汉:武汉大学出版社，1996. [4] 卢万铮.天线理论与技术[M] .西安：西安电子科技大学出版社，2004. The Realization of MATLAB on Array Antenna's Radiation Pattern Chen Tian-lu Guo Yan-hong （ School of ScienceTibet University Lhasa, Tibet 850000) Abstract: The directivity of Antenna refers to the spatial distribution rule of electromagnetic radiation in the space. The present paper analyzes the directivity of the uniform and non-uniform linear array antenna, the ar－ ray antenna's directional function F (θ, φ) as the key object. In addition, the variation characteristics of direc－ tion of maximum radiation and the width of main lobe with the parameters change in the array antenna radia－ tion pattern have been discussed and a two and three-dimensional figure of antenna radiation was plotted eas－ ily by using MATLAB, which showed the distribution rule of radiation field in the space intuitively and the characteristics of the radiation pattern clearly. Key Words: Array Antenna; Radiation Pattern; MATLAB 责任编辑：蔡秀清 ] [ - 107 -

免费论文查重：http://free.paperyy.com 3亿免费文献下载：http://www.ixueshu.com 超值论文自动降重：http://www.paperyy.com/reduce_repetition PPT免费模版下载：http://ppt.ixueshu.com -------------------------------------------------------------------------------

资料库

阵列天线方向图的MATLAB实现.pdf

相关推荐

行业

热门标签

最新资料