2014年四川省达州市中考数学真题及答案.doc-资料库

第1页 / 共7页

第2页 / 共7页

第3页 / 共7页

第4页 / 共7页

第5页 / 共7页

第6页 / 共7页

第7页 / 共7页

2014 年四川省达州市中考数学真题及答案共 30 分）本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷 1 至 2 页，第Ⅱ卷 3 至 10 页。考试时间 120 分钟，满分 120 分。第 I 卷（选择题温馨提示：答第卷前，请考生务必将姓名、准考证号、考试科目等按要求填涂在机读卡上。每小题选出正确答案后，请用 2B 铅笔把机读卡上对应题号的答案标号涂黑。考试结束后，请将本试卷和机读卡一并交回。选择题：（每小题 3 分，共 30 分）向东行驶 3km,记作+3km，向西行驶 2km 记作 B A. +2km 2、2014 年 5 月 21 日，中国石油天然气集团公司与俄罗斯天然气工业股份公司在上海签署了《中俄东线供气购销合同》，这份有效期为 30 年的合同规定，从 2018 年开始供气，每年的天然气供应量为 380 亿立方米，380 亿立方米用科学记数法表示为 A A. D. 3.8×1011m3 C. 380×108m3 B. 38×109m3 3.8×1010m3 C. +3km D. -3km B. -2km 3、二次根式 2 4x  有意义，则实数 x 的取值范围是 D x≥-2 A. 4、小颖同学到学校领来 n 盒粉笔，整齐地摞在讲桌上，其三视图如图所示，则 n 的值是 B B. x＞-2 D. x≤2 C. x＜2 A．6 B. 7 C. 8 D. 9 5、一家特色煎饼店提供厚度相同、直径不同的两种煎饼，甲种煎饼直径 20 厘米卖价 10 元，乙种煎饼直径 30 厘米卖价 15 元，请问：买哪种煎饼划算？B A. 甲 D.无法确定 C. 一样 B. 乙 6、下列说法中错误的是 C A. 将油滴入水中，油会浮出水面是一个必然事件 B．1、2、3、4 这组数据的中位数是 2.5 C. 一组数据的方差越小，这组数据的稳定性越差 D．要了解某种灯管的使用寿命，一般采用抽样调查 7、如图，在四边形 ABCD 中，∠A+∠D=，∠ABC 的平分线与 ∠BCD 的平分线交于点 P，则∠P=C 1 2   1 2 90 A. B. 0 0 90 1 2  C. D. 0 360 

b＞0 B.k＜0 8、直线 y=kx+b 不经过第四象限，则 c A.k＞0 9、如图，以点 O 为支点的杠杆，在 A 端用竖直向上的拉力将重为 G 的物体匀速拉起，当杠杆 OA 水平时，拉力为 F；当杠杆被拉至 OA1 时，拉力为 F1，过点 B/作 B1C⊥OA，过点 A1 作 A1D ⊥OA，垂足分别为点 C、D。 C. k＞0 b≥0 D. k＜0 b≥0 b＞0 ① 10B C ∽ 10A D ②OA.OC=OB.OD ③OC.G=OD.F1 ④F=F1 上述 4 个结论中，正确结论有 D A．1 个 B. 2 个 C. 3 个 D. 4 个 10、右图是二次函数 y  2 ax  bx  的图象的一部分，对称轴是直线 X=1 c ② 4a-2b+c＜0 ① b2＞4ac ③ 不等式 ax2+bx+c＞0 的解集是 x≥3.5 ④若（-2，y1）,(5,y2)是抛物线上的两点，则 y1＜y2 上述 4 个判断中，正确的是 B A．①② C．①③④ B. ①④ D. ②③④ 共 90 分）第 II 卷（非选择题温馨提示：答第Ⅱ卷前，请考生务必将座位号和密封线内相关内容要求写在规定的位置。用蓝、黑色墨水钢笔或圆珠笔将答案直接写在试卷上，不能使用铅笔和涂改液。填空题（本题 6 个小题，每小题 3 分，共 18 分。把最后答案直接填在题中的横线上） 11、化简：（-a2b3）3=-a6b9 12、“每天锻炼一小时，健康生活一辈子”，自开展“阳光体育运动”以来，学校师生的锻炼意识都增强了，某校有学生 8200 人，为了解学生每天的锻炼] 时间，学校体育组随机调查了部分学生，统计结果如表所示。表格中，m= 这组数据的众数是该校每天锻炼时间达到 1 小时的约有人。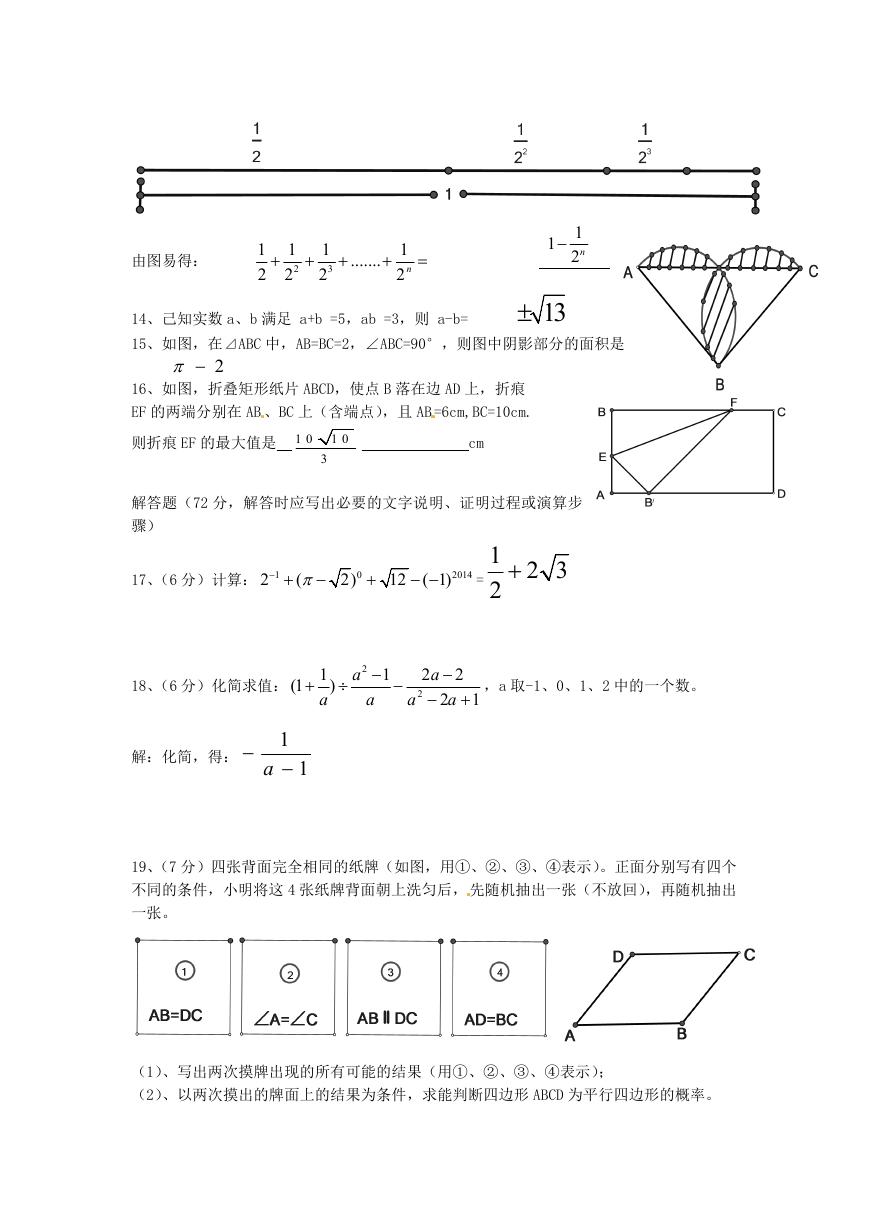 13、《庄子。天下篇》中写道：“一尺之棰，日取其半，万世不竭”意思是：一根一尺的木棍，如果每天截取它的一半，永远也取不完，如图所示。 29 分钟及以下 1 小时及以上 3 0-39 分钟 40-49 分钟 50-59 分钟； 820 时间段 0.54 0.12 24 m 18 20 0.15 0.09 频数 108 频率 30 108 ; 0.1

由图易得： 1 2  1 2 2  1 3 2  .......  1 2 n  14、己知实数 a、b 满足 a+b =5，ab =3，则 a-b= 1 1 2n 13 15、如图，在⊿ABC 中，AB=BC=2，∠ABC=90°，则图中阴影部分的面积是 2  16、如图，折叠矩形纸片 ABCD，使点 B 落在边 AD 上，折痕 EF 的两端分别在 AB 、BC 上（含端点），且 AB =6cm,BC=10cm. 则折痕 EF 的最大值是 1 0 1 0 cm 3 解答题（72 分，解答时应写出必要的文字说明、证明过程或演算步骤） 17、（6 分）计算： 1 2    ( 0 2)  12 ( 1)   2014 = 1 2  2 3 18、（6 分）化简求值： (1  1 a )  a 1 2  a  2 a 2  2  2 a  1 a ，a 取-1、0、1、2 中的一个数。解：化简，得：  1  1 a 19、（7 分）四张背面完全相同的纸牌（如图，用①、②、③、④表示）。正面分别写有四个不同的条件，小明将这 4 张纸牌背面朝上洗匀后，先随机抽出一张（不放回），再随机抽出一张。（1）、写出两次摸牌出现的所有可能的结果（用①、②、③、④表示）；（2）、以两次摸出的牌面上的结果为条件，求能判断四边形 ABCD 为平行四边形的概率。

解：（1）①——② ②----①- ①——③ ——④ ③---① ①——④ ④——① ② ④___② ②——③ ③——② ③——④ ④ ——③ （2） 5 6 （7 分）某服装商预测一种应季衬衫能畅销市场，就用 8000 元购进一批衬衫，面市后果然供不应求，服装商又用 17600 元购进了第二批这种衬衫，所购数量是第一批购进数量的 2 倍，但单价贵了 8 元。商家销售这种衬衫时每件定价都是 100 元，最后剩下 10 件按八折销售，很快售完。在这两笔生意中，商家共盈利多少元？解：设进价为 X 元，则：  1 7 6 0 0 8 x  ， 8 0 0 0  2 x X=80 盈利 4200 元。 21、如图，直线 PQ 与⊙O 相交于点 A、B，BC 是⊙O 的直径，BD 平分∠CBQ 交⊙O 于点 D，过点 D 作 DE⊥PQ，垂足为 E。（1）求证：DE 与⊙O 相切；（2）连结 AD，己知 BC=10，BE=2，求 sinBAD 的值。解：(1 )连接 OD,CD,证明 OD 平行于 AQ. D B E (2) 证明 C B D   , 把 BAD 转化成 BCD ，答案为 5 5 .

22、（8 分）达州市凤凰小学位于北纬 21°，此地一年中冬至日正午时刻，太阳光与地面的夹角最小，约为 35.5°；夏至日正午时刻，太阳光的夹角最大，约为 82.5°。己知该校一教学楼窗户朝南，窗高 207cm，如图（1）请你为该窗户设计一个直角形遮阳棚 BCD，如图（2）所示，要求最大限度地节省材料，夏至日正午刚好遮住全部阳光，冬至日正午能射入室内的阳光没有遮挡。（1）在图（3）中画出设计草图；（2）求 BC、CD 的长度（结果精确到个位） ( 参考数据： sin35.5 ° ≈ 0.58, sin82.5°≈0.99,cos82.5°≈0 .13,tan82.5°≈7.60) cos35.5 ° ≈ 0.81, tan35.5 ° ≈ 0.71, (1) 解：BC=37.04 SIN35.5=21（厘米） CD＝37.04 COS35.3=30(厘米) (2) (3) 23、（8 分）如图，直线 L：y=-x+3 与两坐标轴分别相交于点 A、B。（1）当反比例函数 my  x (m＞0,x＞0)的图象在第一象限内与直线 L 至少有一个交点时，求 m 的取值范围。（2 若反比例函数 my  x (m＞0,x＞0)在第一象限内与直线 L 相交于点 C、D，当 CD= 2 2 时，求 m 的值。（3）在（2）的条件下，请你直接写出关于 x 的不等式-x+3＜ m x 的解集。解：（1） 0 m 9 4

（2）（3） 5 4 x 或  1 2 x  5 2 24、（10 分）倡导研究性学习方式，着力教材研究，习题研究，是学生跳出题海，提高学习能力和创新能力的有效途径。下面是一案例，请同学们认真阅读、研究，完成“类比猜想” 及后面的问题。习题解答：习题如图（1），点 E、F 分别在正方形 ABCD 的边 BC、CD 上，∠EAF=45°，连接 EF，则 EF=BE+DF，说明理由。解答：∵正方形 ABCD 中，AB=AD，∠BAD=∠ADC=∠B=90°， ∴把⊿ABE 绕点 A 逆时针旋转 90°至⊿ADE/ ，点 F、D、E/在一条直线上。 ∴∠E/AF=90°-45°=45°=∠EAF，又∵AE/=AE，AF=AF ∴⊿AE/F≌⊿AEF（SAS） ∴EF=E/F=DE/+DF=BE+DF。习题研究观察分析别在边 BC、CD 上；②AB=AD；③∠B=∠D=90°；观察图（1），由解答可知，该题有用的条件是①ABCD 是四边形，点 E、F 分 ④  EAF   1 2 BAD 。答：成立。类比猜想（1）在四边形 ABCD 中，点 E、F 分别在 BC、CD 上，当 AB=AD， ∠B=∠D，  EAF   1 2 BAD 时，还有 EF=BE+DF 吗？答：不一定成立。研究一个问题，常从特例入手，请同学们研究：如图（2），在菱形 ABCD 中，点 E、F 分别在 BC、CD 上，当∠BAD=120°，∠EAF=60° 时，还有 EF=BE+DF 吗？答：BE+DF  EF.  （2）在四边形 ABCD 中，点 E、F 分别在 BC、CD 上，当 AB=AD，∠B+∠D=180， EAF 时，EF=BE+DF 吗？答：成立。   1 2 BAD

归纳概括一般命题：反思前面的解答，思考每个条件的作用，可以得到一个结论“EF=BE+DF”的  在四边形 ABCD 中，点 E、F 分别在 BC、CD 上，当 AB=AD，∠B+∠D=180， EAF   1 2 BAD 时，总有 EF=BE+DF 成立。 25、（12 分）如图，在平面直角坐标系中，己知点 O（0，0），A（5，0），B（4，4）。（1）求过 O、B、A 三点的抛物线的解析式。（2）在第一象限的抛物线线上存在点 M，使以 O、A、B、M 为顶点的四边形面积最大，求点 M 的坐标。（3）作直线 x=m 交抛物线于点 P，交线段 OB 于点 Q，当 PQB 为等腰三角形时，求 m 的值。解：（1） y  x 52  x （2）M(2 ,6) (3) 12或m

资料库

2014年四川省达州市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料