基于SVPWM三相逆变器在MATLAB下的仿真研究.doc-资料库

weixin_43723191-11138865-4744300845146202363.doc.pdf-第1页.png

第1页 / 共8页

weixin_43723191-11138865-4744300845146202363.doc.pdf-第2页.png

第2页 / 共8页

weixin_43723191-11138865-4744300845146202363.doc.pdf-第3页.png

第3页 / 共8页

weixin_43723191-11138865-4744300845146202363.doc.pdf-第4页.png

第4页 / 共8页

weixin_43723191-11138865-4744300845146202363.doc.pdf-第5页.png

第5页 / 共8页

weixin_43723191-11138865-4744300845146202363.doc.pdf-第6页.png

第6页 / 共8页

weixin_43723191-11138865-4744300845146202363.doc.pdf-第7页.png

第7页 / 共8页

weixin_43723191-11138865-4744300845146202363.doc.pdf-第8页.png

第8页 / 共8页

基于 SVPWM 三相逆变器在 MATLAB 下的仿真研究摘要：介绍了电压空间矢量脉宽调制控制算法的基本概念; 并简要介绍了利用多种实际矢量合成所需电压矢量的方法及具体的实现算法; 最后，利用 Matlab 的 Simulink 工具箱，建立了 SVPWM 逆变器的仿真模型，通过仿真波形可知，该算法是正确的，并分析了逆变器输出的交流电压和电流的谐波。关键词：SVPWM、Simulink、三相逆变器 0 引言电压空间矢量脉宽调制( Space Vector PWM，SVPWM) 控制技术，也称作磁链跟踪控制技术，它是从控制交流电动机的角度出发，最终目的是在电动机气隙空间形成旋转磁场，从而产生恒定的电磁转矩。空间矢量脉宽调制方法凭借其优越的性能指标、易于数字化实现等优点，自提出以来就成为研究的热点，不仅可以应用在各种交流电气传动系统中，而且在电力系统功率因数的调节以及各种利用清洁能源发电的分布式发电系统中都有很好的应用前景。 1 SVPWM 逆变器的原理 1.1 电压空间矢量电压空间矢量是研究交流电动机三相电压与电动机旋转磁场关系而提出的虚构物理量。在空间按 120°对称分布的三相电机定子绕组上施加三相对称电压 Uu  a Uu  b m sin( m sin t          t  2  )  3 2  ) 3   1 Uu c  m sin( t  在定子绕组中即产生定子电流和磁通。对单个绕组而言，产生的磁通是脉振的，它仅在固定的绕组轴线位置上有大小和方向的变化，但是在三相绕组的共同作用下，在电机的气隙中就产生了合成的旋转磁场。电压和电流是时间变量，并没有空间的概念，但是电动机三相绕组产生的旋转磁场是空间和时间的变量，它的大小和空间位置随时间变化，一般以矢量表示。时空变化的旋转磁场由三相电压产生，为了描述三相电压与电动机旋转磁场的关系，提出了电压空间矢量的概念。

电压空间矢量反映了三相电压综合作用的效果，三相电压与电压空间矢量的关系由 Park 变换来表示: u S  2 3  j 0 ( eu A  eu B j 120   eu C j 240  ) )2( 式中，us 为电压空间矢量，uA、uB、uC 为三相相电压，2/3 为变换系数，指数项表示了三相绕组的空间位置。 1.2 逆变器开关状态与电压空间矢量六开关三相桥式逆变器的基本结构如图 1 所示，三相上下桥臂的开关以 SA、SB、SC 表示，且令 SA、SB、SC= 1，是该相上桥臂开关接通;SA、SB、SC= 0，是该相下桥臂开关开通。因为上下桥臂开关状态互补，该电路有 23= 8 种可能的开关组合。图 1 三相逆变器基本结构将 uA、uB、uC 代入 Park 变换( 式( 2) ) ，可得逆变器六种开关工作状态下的电压空间矢量 us1～ us6( 表 1) 。开关状态 000 和 111，即下桥臂开关 K4、K6、K2 或上桥臂开关 K1、 K3、K5 同时导通，空间电压矢量 us7= us8= 0。表 1 逆变器开关状态和电压空间矢量 1.3 电压空间矢量和电动机定子磁链轨迹引入电压空间矢量后，三相电动机定子电压方程为 )( tu s  iR ss )( t  )( t d  s dt )5( 式中，φs( t) 为定子磁链，且 us( t) 、is( t) 、φs( t)均为矢量。

图 2 空间电压矢量和磁链轨迹由式( 5) 可得定子磁链为 s ( t) =  u s  (t) －t  dt (t) i ss )6( 忽略定子电阻 Rs，则 s  ( t) = s u (t) dt )6( 根据式( 7) 可以得到定子磁链的运动轨迹。设 t0 时刻定子磁链为 φs0，其位置如图 2 所示。在 t0 时，如果选择开关状态 S1( 011) ，则 us= us1，由式( 7) 定子磁链运动轨迹为 ψ s ( t) ≈  u (t)dt= 1 s 4 3 jπ Ee  Δt  ψ s 0 定子磁链 ψs，从初始值 ψs0 开始，并沿空间电压矢量 us1 的方向移动，ψs 是 ψs0 和 us1 时间增量的矢量和。运行到 t1 时刻，逆变器开关状态切换为 S2( 001) ，定子电压矢量取 us2，同样可以按式( 7) ，决定定子磁链 ψs 的轨迹。之后在 t2～ t5 时刻依次切换逆变器开关状态，电压空间矢量 us3～ us6 依次作用，若 us1～ us6 作用时间相同，该磁链轨迹为正六边形。定子磁链 ψ s 的旋转速度为 ω，ω 取决于开关状态 S1～S6 切换的循环周期 T =1/f，ω =2πf。六节拍逆变器开关 K1～ K6 相隔 60°依次通断，逆变器输出电压为六阶梯波，以电压空间描述，就是 us1～ us6 的依次作用，产生的定子磁链为六边形，与电动机在正弦电压供电时的圆形磁链轨迹有很大不同。六边形磁链轨迹的幅值是变化的，定子磁链幅值的变化必然带来定子转矩的波动，影响电动机的转速稳定。所以，为了电动机的转速稳定，只能产生一个沿圆形轨迹移动的 ψs，由上面叙述可知，只需产生一个以圆形为轨迹运动的 us。

2 SVPWM 逆变器的算法仿真我们可以将 SVPWM 逆变器的控制方案可以分为四个部分: 确定期望合成的电压矢量的扇区位置; 计算分配到相邻非零矢量以及零矢量的作用时间; 确定矢量合成的最佳序列选择; 根据各基本矢量的作用时间合成三相 PWM 信号。 2.1 合成矢量 U*所处扇区的判断将 U*分解( α，β) 到坐标轴上得到 Uα，Uβ，通过 Uα，Uβ的数学关系便可以计算出 U* 所处的扇区，各扇区对应的充要条件见表 2。表 2 各扇区所对应的充要条件定义 A，B，C，若 Uβ＞ 0，则 A = 1，否则 A = 0; 若槡 3 U   U   0 ，则 B = 1，否则 B = 0; 否则  3 U   U   0 ，则 C = 1，否则 C = 0。令 N =4 × C +2 × B + A，不同的 N 值对应着不同的扇区，具体对应关系如表 3。表 3 不同的 N 值所对应的扇区 N 扇区 1 Ⅰ 5 Ⅱ 4 Ⅲ 6 Ⅳ 2 Ⅴ 2.2 各扇区基本矢量作用时间的计算由式( 9) 可以计算出 U*在各个扇区中各矢量的作用时间，具体结果见表 4。表 4 各扇区基本空间矢量的作用时间

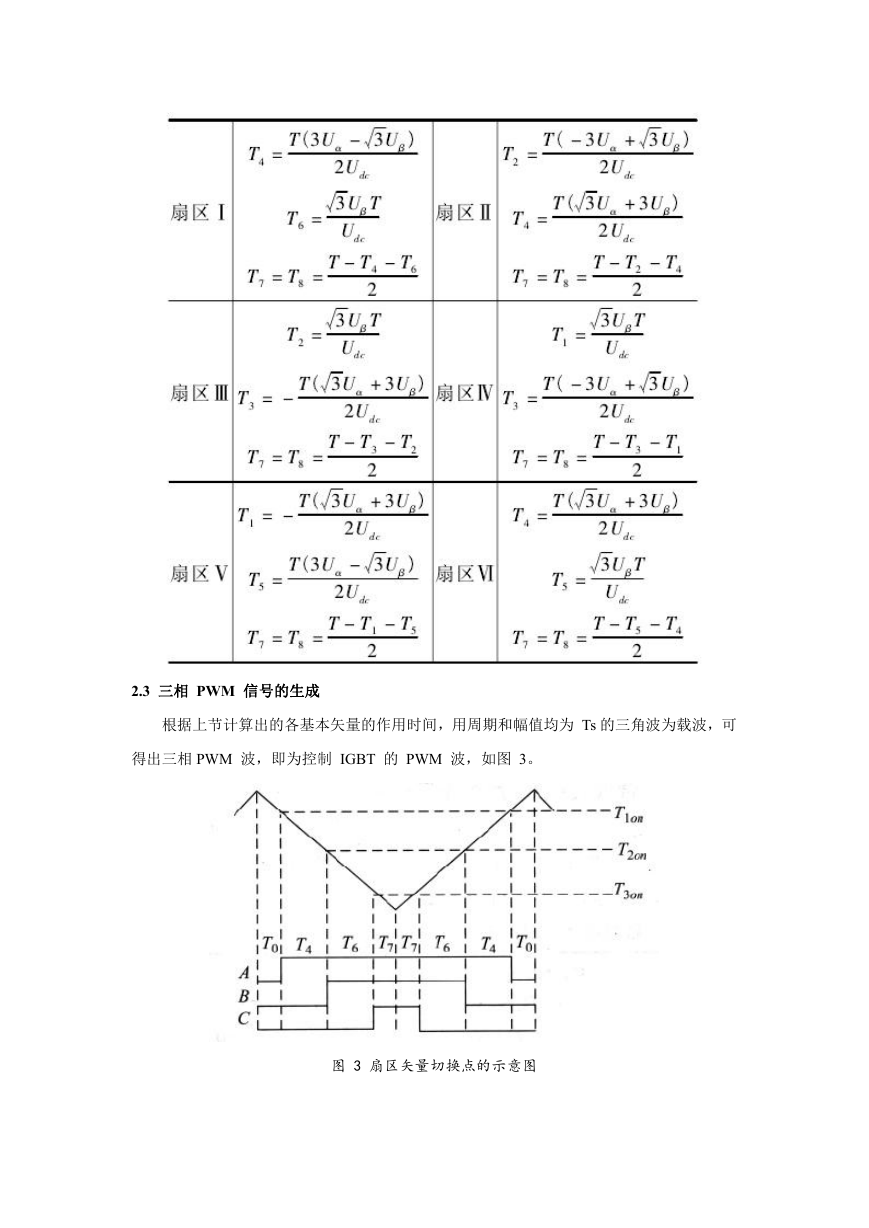
2.3 三相 PWM 信号的生成根据上节计算出的各基本矢量的作用时间，用周期和幅值均为 Ts 的三角波为载波，可得出三相 PWM 波，即为控制 IGBT 的 PWM 波，如图 3。图 3 扇区矢量切换点的示意图

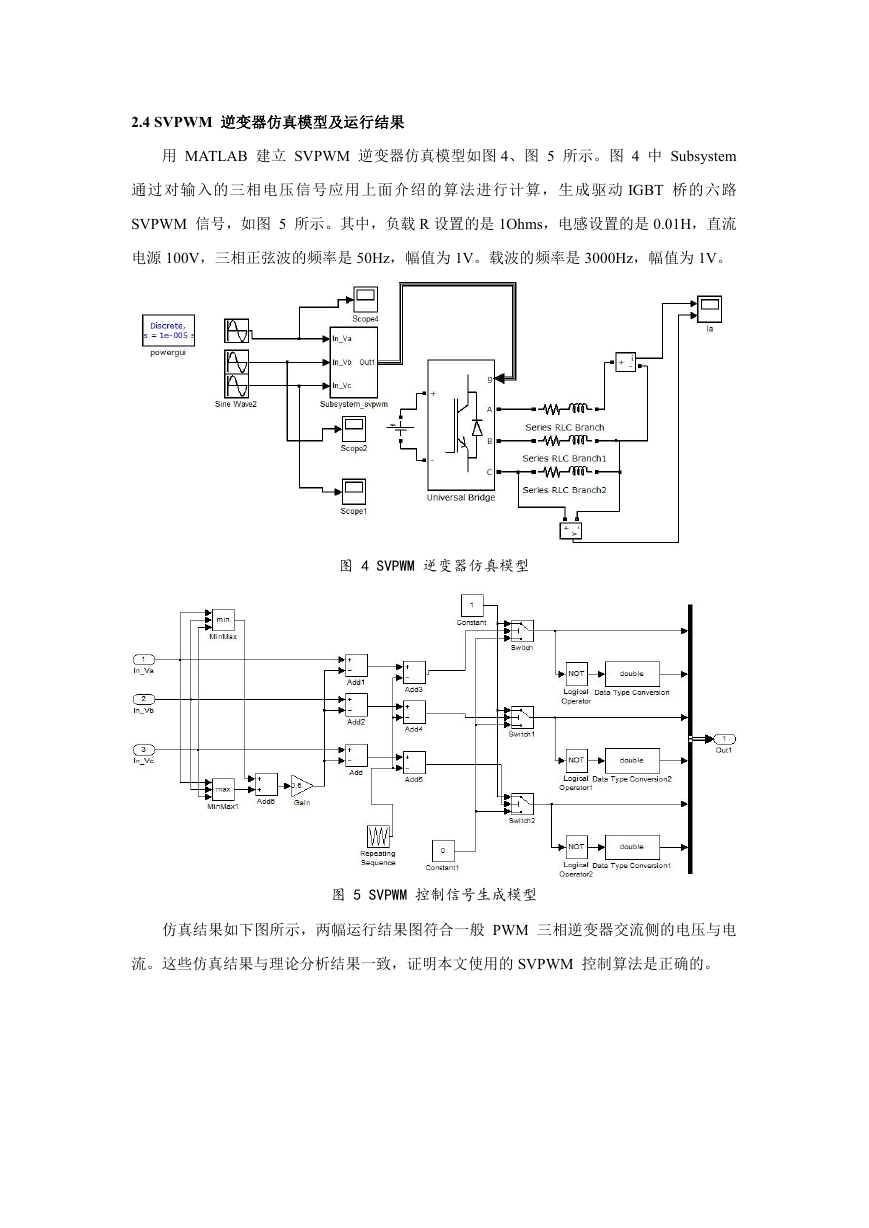
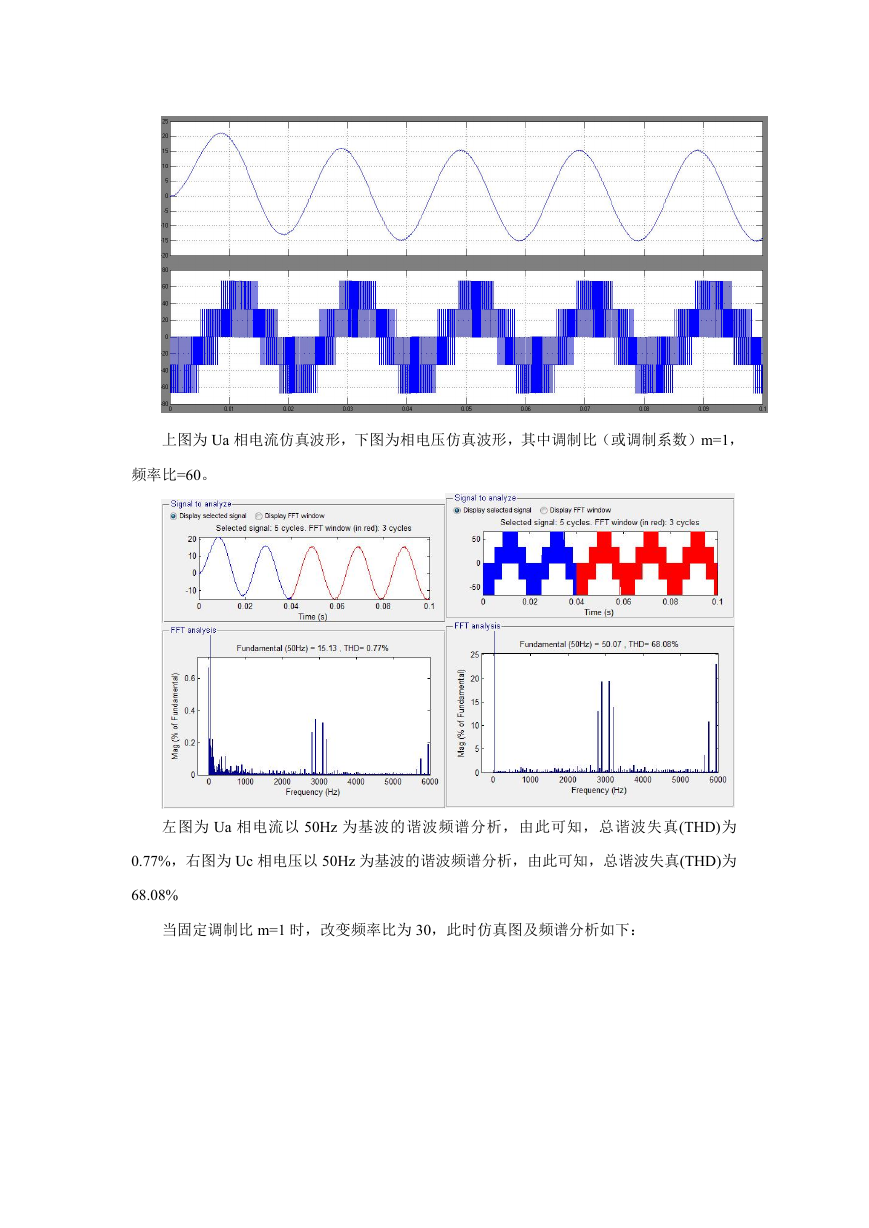
2.4 SVPWM 逆变器仿真模型及运行结果用 MATLAB 建立 SVPWM 逆变器仿真模型如图 4、图 5 所示。图 4 中 Subsystem 通过对输入的三相电压信号应用上面介绍的算法进行计算，生成驱动 IGBT 桥的六路 SVPWM 信号，如图 5 所示。其中，负载 R 设置的是 1Ohms，电感设置的是 0.01H，直流电源 100V，三相正弦波的频率是 50Hz，幅值为 1V。载波的频率是 3000Hz，幅值为 1V。图 4 SVPWM 逆变器仿真模型图 5 SVPWM 控制信号生成模型仿真结果如下图所示，两幅运行结果图符合一般 PWM 三相逆变器交流侧的电压与电流。这些仿真结果与理论分析结果一致，证明本文使用的 SVPWM 控制算法是正确的。

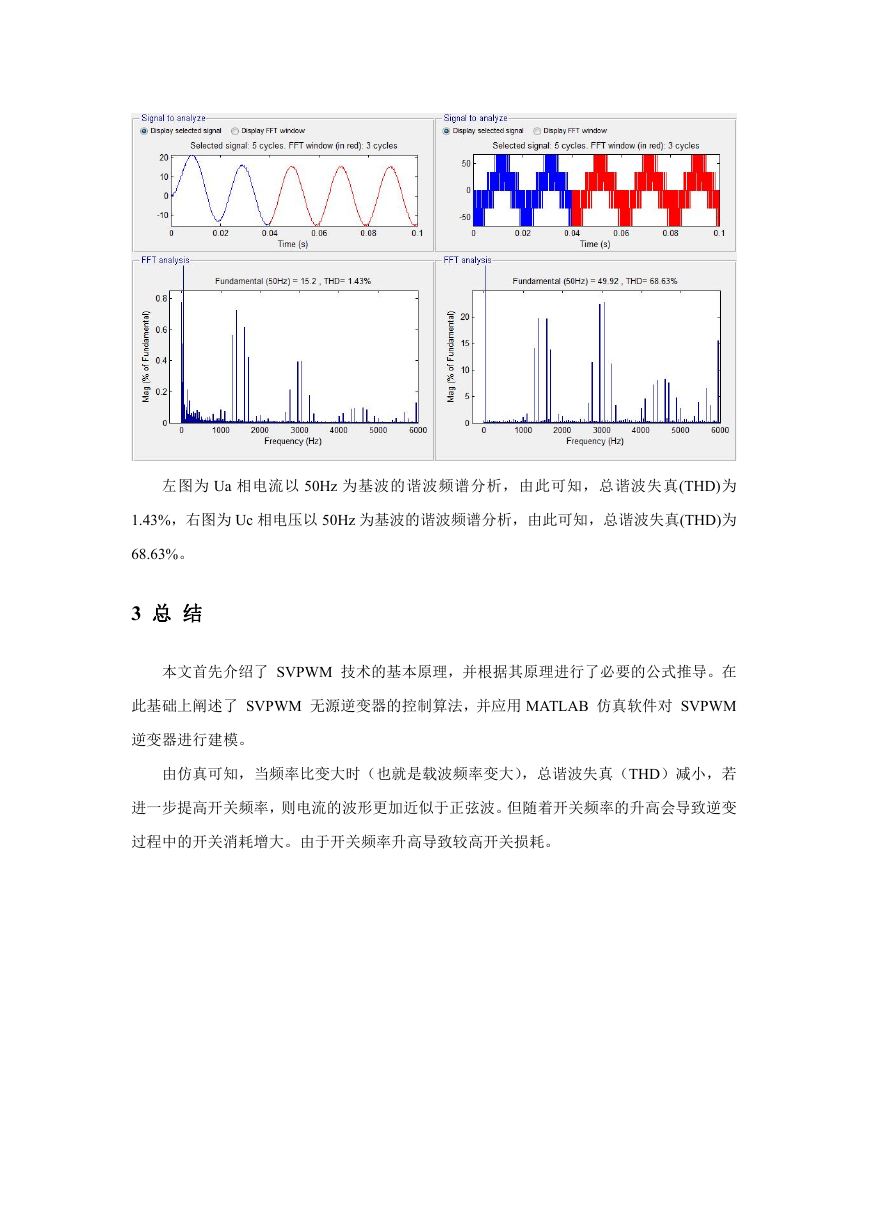
上图为 Ua 相电流仿真波形，下图为相电压仿真波形，其中调制比（或调制系数）m=1，频率比=60。左图为 Ua 相电流以 50Hz 为基波的谐波频谱分析，由此可知，总谐波失真(THD)为 0.77%，右图为 Uc 相电压以 50Hz 为基波的谐波频谱分析，由此可知，总谐波失真(THD)为 68.08% 当固定调制比 m=1 时，改变频率比为 30，此时仿真图及频谱分析如下：

左图为 Ua 相电流以 50Hz 为基波的谐波频谱分析，由此可知，总谐波失真(THD)为 1.43%，右图为 Uc 相电压以 50Hz 为基波的谐波频谱分析，由此可知，总谐波失真(THD)为 68.63%。 3 总结本文首先介绍了 SVPWM 技术的基本原理，并根据其原理进行了必要的公式推导。在此基础上阐述了 SVPWM 无源逆变器的控制算法，并应用 MATLAB 仿真软件对 SVPWM 逆变器进行建模。由仿真可知，当频率比变大时（也就是载波频率变大），总谐波失真（THD）减小，若进一步提高开关频率，则电流的波形更加近似于正弦波。但随着开关频率的升高会导致逆变过程中的开关消耗增大。由于开关频率升高导致较高开关损耗。

资料库

基于SVPWM三相逆变器在MATLAB下的仿真研究.doc

相关推荐

行业

热门标签

最新资料