70 第 25 卷第 11 期 2009 年 11 月 电 力 科 学 与 工 程 Electric Power Science and Engineering Vol.25, No.11 Nov., 2009 基于 MATLAB 的 NURBS 曲面造型研究 陈庆雪 1，韩庆瑶 2 （1.保定标正机床有限责任公司，河北 保定 071000；2.华北电力大学 能源与动力工程学院，河北 保定 071003） 摘要：根据 3 次 NURBS 曲面的矩阵表达式，通过反求 NURBS 曲面的权因子和控制顶点，完成了对 3 次 空间 NURBS 曲面的插值；并在此基础上，结合蒙面法构造了空间 2×3 次 NURBS 曲面；最后利用 MATLAB 软件对曲面进行了生成，验证了该算法的准确性和可行性。 关键词：NURBS 曲面；反求；蒙面法 中图分类号：TP393.0 文献标识码：A 0 引 言 NURBS (Non-Uniform Rational B-Spline) 自从被提出以来，其良好的特性受到了工程界的重 视。NURBS 方法已成为 IGES 标准和 STEP 标准 中描述产品几何形状的唯一方法，并已在 CAD/ CAM 和计算机图形学领域得到越来越广泛的应用。 NURBS 插值在构造曲线曲面及进行形状表示 与设计中有着重要的意义，但目前的研究大多是对 空间 NURBS 曲线的插值，对 NURBS 曲面的插值 研究并不多。基于国内外的研究成果，在对 NURBS 曲线的插值基础上，利用蒙面法对空间 2×3 次 NUR- BS 曲面的生成进行了研究。 1 NURBS 曲面的表达式 1.1 NURBS 曲面的有理表达式 基于 NURBS 曲线，一张 k×l 次的 NURBS 曲 面可以用以下有理分式表示： , , , , , = =0 =0 , , , =0 =0 这里控制顶点 , =0,1,…, ; =0,1,…, 呈拓 扑矩形阵列，形成一个控制网格。 , 是与顶点 , 联 0, , , >0，其余 , 系的权因子，规定四角顶点处用正权因子即 0,0, ,0, 0 且顺序 × 个权因子不同时为 零， , 和 , 分别为沿 向的 次和沿 向的 次 B 样条基函数。 向和 向的节点矢量分别为：U= [ 0，1，…， + +1]与 V= [ 0，1，…， + +1] ，按德布尔 递推公式决定。 1.2 NURBS 曲面的矩阵表达式 由于 NURBS 曲面是基于 NURBS 曲线的张量 积形式得到，因此，很容易根据 NURBS 曲线的矩 阵表示拓展到 NURBS 曲面的矩阵表示。 给定空间 +1 × +1 个顶点 , =0,1,…, ; =0,1,…, 它们构成 2× 3 次非均匀有理 B 样条曲 面的特征网格，则相应的 2×3 次非均匀有理 B 样条 曲面方程可以表示为： , = , T T T T , , 0 , 1; =0,1,…, 2, =0,1,…, 3) 12 22 32 13 23 33 +2 2 +1 +1 2 +1 = 2 11 1+ 11 12 11 11+ 33 0 0 +2 2 +2 12 22 32 42 13 23 33 43 = 14 24 34 44 = = 11 21 31 11 21 31 41 收稿日期：2009 08 09. 作者简介： 陈庆雪 (1963 －), 男, 保定标正机床有限责任公司高级工程师. 

第 11 期 2 3 +1 +3 2 +2 1 11 13 3 11 3 11 23 3 11 3 11+ 33 陈庆雪，等 基于 MATLAB 的 NURBS 曲面造型研究 71 2 3 +2 +2 2 +2 3 +3 2 +2 +3 2 +2 +2 3 +2 2 3 +2 0 0 0 控制顶点。 （5）步骤 4 所求得的控制顶点即为用蒙面法构 造 NURBS 曲面的控制顶点，得到 NURBS 曲面。 3 实例验证 11 11 43 44 1 3 33+ 44+ 2 3 +2 +3 2 +3 2 3 +3 +3 2 +3 , , , +1 , +1 , +2 , +2 , +3 , +3 = +1, +1, +1, +1 +1, +1 +1, +2 +1, +2 +1, +3 +1, +3 +2, +2, +2, +1 +2, +1 +2, +2 +2, +2 +2, +3 +2, +3 = , +1, +2, , +1 , +2 , +3 +1, +1 +1, +2 +1, +3 +2, +1 +2, +2 +2, +3 式中 = +1 ； =0, 1, …, + +1 2= + +1= +2 ； =0, 1, …, + 3= + +1+ +2= +3 ； =0, 1, …, + 1 1= + 。。特别地： 0=0。 同理： = + +1+… + 2 NURBS 曲面的生成 曲面生成是曲面造型中的核心技术，最常用的 方法就是蒙面法。蒙面法其实质就是拟合一张光滑 曲面，使其通过一组有序的截面曲线的空间曲线。 它可形象地看成为给一族截面曲线构成的骨架蒙上 一张光滑的皮，其核心就是曲面的反算技术。 蒙面法构造 NURBS 曲面的主要步骤如下： （1）构造截面曲线。首先根据给定的型值点或 曲线的几何形状构造各截面的 NURBS 曲线。当曲 线由不同幂次的曲线段构成时，则以幂次最高者为 准，将低幂次曲线段升阶，而后以统一幂次的 NUR- BS 曲线表示该曲线。 （2）统一各截面曲线的节点矢量。对各截面曲 线的节点矢量 (设为向) 做并运算，使其具有统一 的节点矢量。为保证各截面曲线的形状不变，常插 入节点的算法。在统一节点矢量后，再计算各截面 的控制顶点。 （3）计算 v 向的节点矢量。v 向节点矢量由求 得的控制顶点确定，应取统一数值。为此可取各截 面曲线节点矢量的平均值作为 v 向节点矢量。 （4）以步骤 3 所求得的控制顶点为型值点，并 在求的各点对应权因子的基础上，应用步骤 3 所求 得 v 向节点矢量计算基函数，逐个截面反算 v 向的 为简单起见，取截面曲线为 4 个半径相同的空 间圆，圆心坐标分别为（1，0，1），（2，0，2）， （1，0，3），（2，0，4）。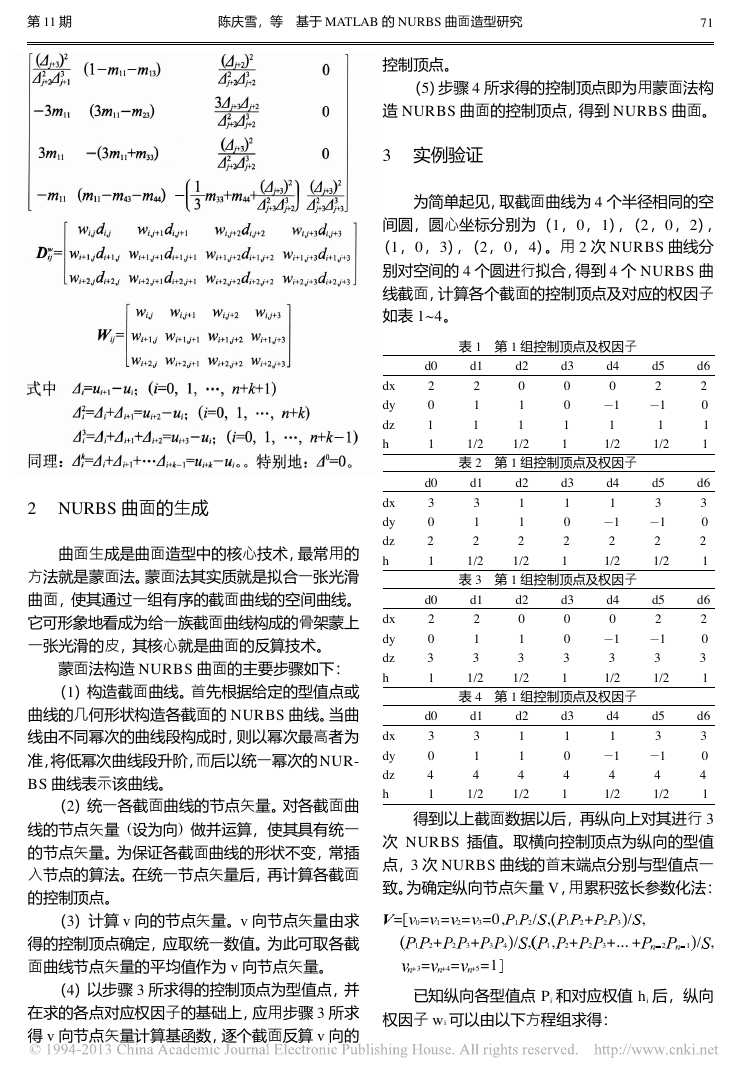用 2 次 NURBS 曲线分 别对空间的 4 个圆进行拟合，得到 4 个 NURBS 曲 线截面，计算各个截面的控制顶点及对应的权因子 如表 1~4。 d0 2 0 1 1 d0 3 0 2 1 d0 2 0 3 1 表 1 第 1 组控制顶点及权因子 d1 2 1 1 1/2 d2 0 1 1 1/2 d3 0 0 1 1 d4 0 1 1 1/2 表 2 第 1 组控制顶点及权因子 d1 3 1 2 1/2 d2 1 1 2 1/2 d3 1 0 2 1 d4 1 1 2 1/2 表 3 第 1 组控制顶点及权因子 d1 2 1 3 1/2 d2 0 1 3 1/2 d3 0 0 3 1 d4 0 1 3 1/2 表 4 第 1 组控制顶点及权因子 d5 2 1 1 1/2 d5 3 1 2 1/2 d5 2 1 3 1/2 d6 2 0 1 1 d6 3 0 2 1 d6 2 0 3 1 dx dy dz h dx dy dz h dx dy dz h dx dy dz h d3 1 0 4 1 d4 1 1 4 1/2 d0 3 0 4 1 d2 1 1 4 1/2 d1 3 1 4 1/2 d5 3 1 4 1/2 d6 3 0 4 1 得到以上截面数据以后，再纵向上对其进行 3 次 NURBS 插值。取横向控制顶点为纵向的型值 点，3 次 NURBS 曲线的首末端点分别与型值点一 致。为确定纵向节点矢量 V，用累积弦长参数化法： = 0= 1= 2= 3=0, 1 1 2+ 2 3+ 3 +3= +4= +5=1 4 / 2/ , , 1, 2+ 2 3 / , 1 2+ 2 3+…+ 2 1 / , 已知纵向各型值点 Pi 和对应权值 hi 后，纵向 权因子 wi 可以由以下方程组求得： 

72 电 力 科 学 与 工 程 2009 年 11, 12, 13 1 +1 0 / / +2 +1, , *= 0 3= 1 +1= *= +1 3 3 T= +1 进而求得曲面整体权因子 。 求得 wi 后，利用下面方程组反算纵向的控制 顶点（其中三次 NURBS 曲线的首末控制顶点 d0， dn+1 就是首末数据点 p1，pn）： 0 1 0 1 2 1 2 2 0 1 2 = +1 +1 +1 0 1 2 +1 1 图 2 蒙面法生成的 NURBS 曲面效果图 4 结 论 0 ， 式中 0=0， 0= 3 1 0 ， 0= 3 1 ， +1= 3 3 0 3 +1 +1 。 3 +1 +1= +1= 3 +1 +1 +1 ， 0= 3 1 0 3 ， +1=0， +1 进而求得曲面整体控制顶点。 用 MATLAB 软件对以上算法进行计算机图形 生成，得到的纵向 NURBS 曲线和用蒙面法得到的 NURBS 曲面效果图分别如图 1,2 所示。 图 1 纵向 NURBS 曲线插值效果图 根据 2× 3 次 NURBS 曲面的矩阵表达式，给 出了空间 NURBS 曲面的插值算法；用蒙面法构造 了空间 NURBS 曲面，利用 MATLAB 对该算法进 行了实验验证并取得的良好的效果。该算法的实 现，为以后对复杂实体的 NURBS 曲面造型进一步 研究奠定了基础。 参考文献： [1] 施法中. 计算机辅助几何设计与非均匀有理 B 样条 [M]. 北京: 北京航空航天大学出版社，1994. [2] 朱心雄. 自由曲线曲面造型技术 [M]. 北京：科学出版 社，2000. [3] 张喜明. 自由曲面造型方法及数控加工轨迹研究 [D]. 保 定：华北电力大学，2001. [4] 董云风. 基于 NURBS 曲面的逼近及数控加工技术的研 究 [D]. 保定：华北电力大学，2006. [5] 韩庆瑶，董云风，师向红. 三次 NURBS 空间曲线的插 值研究 [J]. 煤矿机械，2007，(1)：44-46. Research of NURBS-face Modeling Based on MATLAB Chen Qingxue1, Han Qingyao2 (1. Baoding Biaozheng Machine Tool Co., Ltd., Baoding 071000, China; 2. School of Energy and Power Engineering, Baoding 071003, China) Abstract:Based on the matrix expression of NURBS-face,the interpolation of cubic space NURBS-face is completed by reversing weights and control points of cubic NURBS-face. Then based on that, the 2×3 cubic NURBS-face was constructed by skinning method. In the end, the NURBS-face was generated by using MATLAB, the accuracy and feasibility of the algorithm were proved. Key words: NURBS-face; reserve; skinning-method; MATLAB