第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
2020-2021学年江苏省南通市海安市八年级下学期期中数学试题及答案.doc
2020-2021 学年江苏省南通市海安市八年级下学期期中数学试题及答
案
（试卷总分 150 分 测试时间 120 分钟）
命题：孙庄初中八年级数学组 校对：孙庄初中八年级数学组
一．选择题（每题 3 分）
1．使二次根式
A． 2x
B． 2
2．下列运算，结果正确的是（
2x 有意义的 x的取值范围是（
2
x
x
C．
）
）
D．
2
x
A． 5
3
2
B．3
2
3 2
C． 6
2
3
D． 6
2
2 3
3．小华周六上午从家跑步到离家较远的田园广场，在那里与同学们打一段时间的羽毛球后再漫步回家，下
面能反映小华离家的距离 y与时间 x之间关系的图象的是（
）
A．
B．
C．
D．
4．下列命题中正确的是（
A．对角线相等的四边形是矩形
C．对角线互相平分且相等的四边形是矩形
D．一组对边相等，另一组对边平行的四边形是平行四边形
）
B．对角线互相垂直的四边形是菱形
:l
y
5．直线 1
k x b
1
1
x
A．
k x
2
l
与直线 2
k x b
1
的解集为（
在同一平面直角坐标系中的图象如图所示，则关于 x的不等式
k x
2
:
y
）
B．
x
1
C． 0x
D． 1
x
0
（第 5 题）
（第 6 题）
（第 7 题）
（第 8 题）
6．如图，在四边形 ABCD 中，AC=BD=6，E、F、G、H 分别是 AB、BC、CD、DA 的中点，则 EG2+FH2 的值为（
A．9
7．如图，四边形 ABCD 是菱形，AC＝8，DB＝6，DH⊥AB 于 H，则 DH 等于（ ）
D．48
C．36
B．18
）
A．
48
5
B．
24
5
C．5
D．4
8．如图，在矩形纸片 ABCD 中，AD＝9，AB＝3，将其折叠，使点 D 与点 B 重合，折痕为 EF，那么折痕 EF 的
长为（
）
A．3
B． 6
C． 10
D．9
9．如图所示，直线 y=x+4 与两坐标轴分别交于 A、B 两点，点 C 是 OB 的中点，D、E 分别是直线 AB、y轴上
的动点，则△CDE周长的最小值是（
）
B．3 10
A．3 7
10．如图，点 P是正方形 ABCD内一点，
A． 2 2
B．3 2
PA ，
PD
C． 2 7
1
C． 2 3
D． 2 10
10
，∠APB=135°，则 PB的长为（
）
D．3 3
（第 9 题）
（第 10 题）
（第 13 题）
二．填空题（11 至 13 每题 3 分，14 至 18 每题 4 分）
11． 27 与最简二次根式
12．若点
y 与点
1m 是同类二次根式，则 m＝
2 1
)x
k
22,Q y 都在一次函数
y
(
13,P
或“＝”）
．
1
的图象上，则 1y
2y .（填“＞”、“＜”
13．如图，已知在平行四边形 ABCD中，对角线 AC，BD相交于点 O，AB⊥AC，AB＝1，BC＝5，则对角线 BD
＝
．
14．一次函数 y=（2m＋1）x＋m﹣3 的图象不经过第二象限，则 m的取值范围为
15．如图，在矩形 ABCD中，AD＝2．将∠A向内翻折，点 A落在 BC上，记为 A ，折痕为 DE．若将∠B沿 EA
．
向内翻折，点 B恰好落在 DE上，记为 B，则 AB＝
．
16．平行四边形 ABCD的面积为 36，AB＝5，BC＝9，则 AC的长为
．
（第 15 题）
（第 17 题）
（第 18 题）
17．如图，在平面直角坐标系中，直线 :
l y
1
x 交 x 轴于点 A，交 y轴于点 1A ，点 2A ， 3A ，…在直线 l
，…均为等腰直
2
上，点 1B ，点 2B ， 3B ，…在 x轴的正半轴上，若 1AOB△
角三角形，直角顶点都在 x轴上，则第 n个等腰直角三角形
A B B△
， 2
1
2
A B B 的顶点 nB 的坐标为
n
A B B△
3
， 3
1
n
n
．
18．如图，已知边长为 6 的菱形 ABCD中，∠ABC＝60°，点 E，F分别为 AB，AD边上的动点， BE AF
，
连接 EF交 AC于点 G，CE、CF分别交 BD于点 M，N，下列结论：①△CEF是等边三角形；②∠DFC＝∠EGC；
③若 BE＝3，则 BM＝MN＝DN；④ 2
EF
的序号是
．
三、解答题(共 91 分)
2
BE DF
2
；⑤△ECF面积的最小值为 27 3
4
．其中正确结论
19．(10 分)计算：（1） 3
12
6
2
27
；（2）
18
x
2
x
3
x
2
x
x
2
．
20．(9 分)已知 y与 2x 成正比例，且 1x 时，
6
y .
（1）求 y与 x之间的函数关系式；
（2）设点（a，－2）在（1）中函数的图象上，求 a的值．
21．(9 分)如图，AB=AC，AD=AE，DE=BC，且∠BAD=∠CAE，
求证：四边形 BCDE 是矩形．
22．(11 分)甲、乙两地相距 300km，一辆货车和一辆轿车先后从甲地出发向乙地．如图，线段 OA 表示货车
离甲地距离 y(km)与时间 x(h)之间的函数关系，折线 BCDE 表示轿车离甲地距离 y(km)与时间 x(h)之间
的函数关系．请根据图象，解答下列问题：
(1)线段 CD 表示轿车在途中停留了
(2)求线段 DE 对应的函数解析式；
(3)求轿车从甲地出发后经过多长时间追上货车．
h；
23．(12 分)“戴口罩､勤洗手､少聚会”是新冠肺炎疫情防控的有效措施．为保证防疫口罩供应，某医药公
司保持每月生产甲､乙两种型号的防疫口罩共 20 万只，投入口罩生产的总成本不超过 28 万元，且所有
口罩当月全部售出，其中成本､售价如下表：
口罩型号
甲 乙
成本（元/只） 1
售价（元/只） 1.5
3
6
（1）设该公司每月生产甲种型号口罩 a万只，月利润为 w万元，求 w与 a的函数关系式，并求出自变量的
取值范围；
（2）公司应怎样安排两种型号口罩的产量，可使每月所获利润最大？并求出最大利润．
24．(12 分)△ABC 中，D 是 BC 上一点，
BD ，
2
AD ，
4
DC ，
8
AC
4 5
．
（1）求证：∠BAC=90°；
（2）若 P 是线段 BC 上的一点， ABP△
请直接写出 BP 的长．
是等腰三角形，
25．(13 分)对于平面直角坐标系 xOy中的图形 M，N，给出如下定义：P为图形 M上任意一点，Q为图形 N
上任意一点，如果 P，Q两点间的距离有最小值，那么称这个最小值为图形 M，N间的"距离"，记作 d(M，
N)．特别的，当图形 M，N有公共点时，记 d(M，N)=0．一次函数 y=kx+2 的图像为 L，L 与 y 轴交点为
D，△ABC中，A（0，1），B（-1，0），C（1，0）．
（1）d(点 D，△ABC)=
（2）若 d(L，△ABC)=0，k的取值范围是
（3）函数 y=x+b的图像记为 W，若 d(W，△ABC) 1 ，求出 b的取值范围．
；当 k=1 时，d( L，△ABC)=
；
；
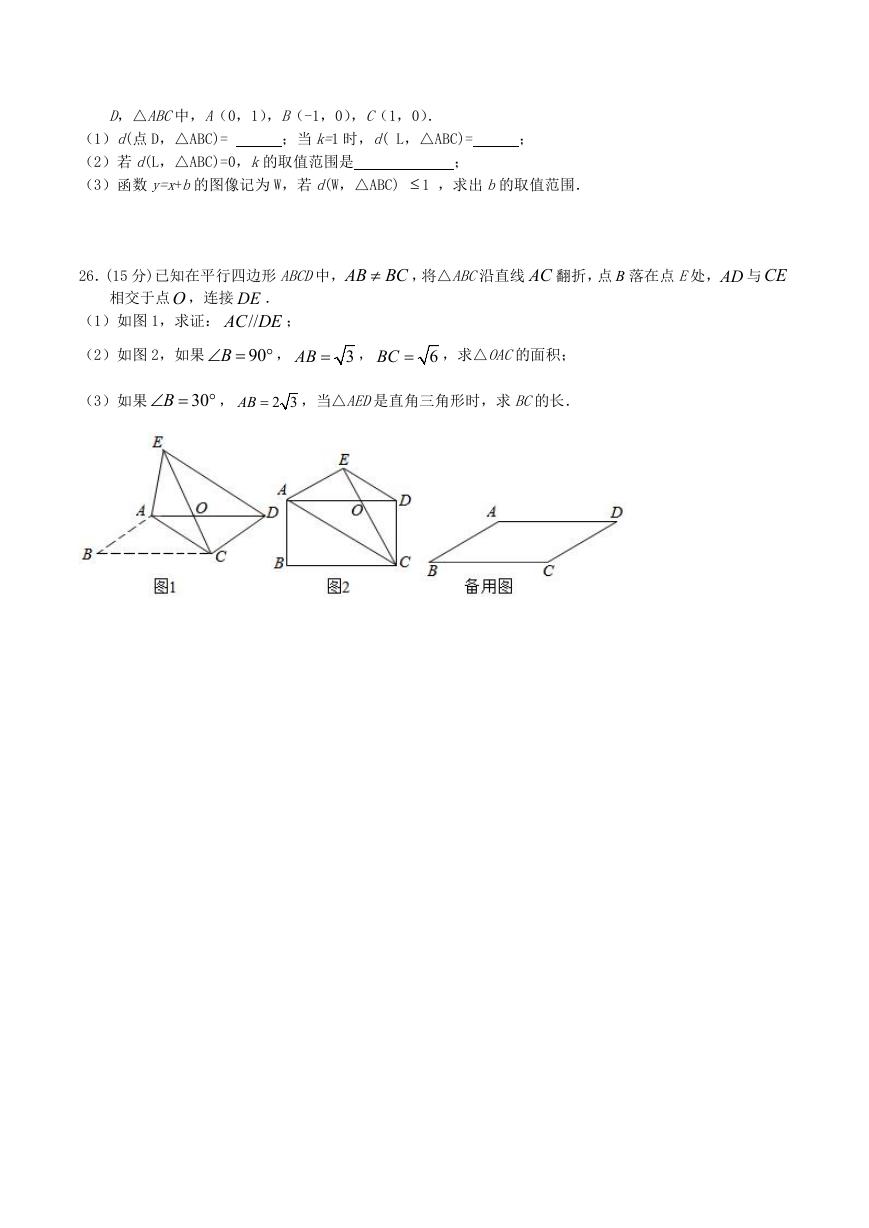
26．(15 分)已知在平行四边形 ABCD中，AB BC ，将△ABC沿直线 AC 翻折，点 B 落在点 E处，AD 与CE
相交于点O ，连接 DE ．
（1）如图 1，求证： //AC DE ；
，
（2）如图 2，如果
B
90
AB ，
3
6BC
，求△OAC的面积；
（3）如果
B
30
，
AB
2 3
，当△AED是直角三角形时，求 BC的长．
一、选择题（每小题 3 分，共 30 分）
八年级数学期中测试参考答案
题号
答案
1
A
2
D
3
D
4
C
5
B
6
C
7
B
8
C
二、填空题（11-13 每小题 3 分，14-18 每题 4 分，共 29 分）
题号 11
12
13
14
15
16
17
10
A
9
D
18
答案 2
>
2 7
三、解答题（共 91 分）
19．（10 分）
1
2
m
3
（1）解：原式＝ 36
3-3 3
3
2 13 4 10或
（ 2
1n ，0） ①②③⑤
＝ 6
3-3 3
………………3 分
＝ 6-2 3
………………5 分
（2）解：原式＝
3 2
x
2
x
x
2
x
＝3 2
x
2
x
2
x
…………8 分
＝5 2x
……………10 分
20．（9 分）
解：（1）设函数解析式为
y
k x
2
k
，其中
0
，…………1 分
∵ 1
x
y
时，
6
，∴3
k ，∴
6
k
2
…………3 分
∴解析式为
y
2
x
，即
2
y
2
x
4
…………5 分
（2）∵（a，-2）在函数图象上，∴ 2
a
∴
a
1
2
4
， …………7 分
…………9 分
21．（9 分）
证明：连接 BD，CE，
∵∠BAD=∠CAE，
∴∠BAE=∠CAD．
又∵AB=AC，AE=AD，
∴△ABE≌△ACD（SAS） .…………3 分
∴BE=CD．
又∵DE=BC，
∴四边形 BCDE 为平行四边形．…………5 分
∵AC=AB，AE=AD，∠CAE=∠BAD，
∴△ACE≌△ABD（SAS）， …………7 分
∴CE=BD．
∴四边形 BCED 为矩形 .
22．（11 分）
解：（1）0.5 ； …………2 分
（2）设线段 DE 对应的函数解析式为 y=kx+b（k≠0），
∵D 点坐标为（2.5，80），E 点坐标为（4.5，300），
.…………9 分
∴
2.5
4.5
k b
k b
80
300
，解得
110
k
195
b
．
…………5 分
∴线段 DE 对应的函数解析式为：y=110x－195（2.5≤ x ≤4.5）．……6 分
（3）设线段 OA 对应的函数解析式为 y=mx（m≠0），
∵A 点坐标为（5，300），
∴5m=300，解得 m=60．
∴线段 OA 对应的函数解析式为 y=60x（0≤ x ≤5） …………8 分
令 60x=110x－195，解得 x=3.9．
∴3.9－1=2.9（小时）
答：轿车从甲地出发后经过 2.9 小时追上货车．
23．（12 分）
………………11 分
…………10 分
解：（1）由题意得：
w
1.5 1
a
6 3 20
a
（2）∵在
w
中，
60
k
5
2
0
∴w随 a的增大而减小 ……9 分
∴当 16
a 时，w取得最大值，
w
最大值
5 16 60 20
2
（万元）……11 分
此时， 20
a
20 16
（万只）
4
……………………12 分
答：应安排生产甲型号口罩 16 万只，乙型号口罩 4 万只，可使每月所获利润最大，最大利润为 20 万元．
24．（12 分）
5
2
a
60
……4 分
…………6 分
…………7 分
a
28
∴ 16
a
∴16
a
20
∵
a
又∵ 0
3 20
20
a
5
2
a
（1）证明：
∵
AD ，
4
DC ，
8
AC
4 5
，且
2
4
2
8
4 5
2
，
∴ 2
AD CD
2
2
AC
， ∴∠ADC=90°，
…………2 分
∴∠ADB=90°，
∴在 Rt△ADB 中，
AB
2
AD BD
2
∵
BC BD DC
10
，
AC
4 5
2
4
，且
2
2
2
2 5
2
， …………4 分
2 5 + 4 5 =10 ，
2
∴ 2
AB
2
AC
2
BC
，
∴∠BAC=90°．
………………6 分
（2）BP 的长为 2 5 或 4 或 5．
………………12 分（每个 2 分）
25．（13 分）
（1）1 ；
2
2
；……………………4 分（每空 2 分）
（2）k≥2 或 k≤−2 ；……………………8 分
（3）函数 y=x＋b的图象 W 与 x轴、y轴交点所围成的三角形是等腰直角三角形，
并且函数 y=x＋b 的图象与 AB 平行，
当 d（W，△ABC）＝1 时，如图所示：
在△AGM 中，∠AGB=90°，AG＝GM＝1，
则 AM＝ 2 ，∴OM＝1
2 ，∴M（0，1
2 ），
此时 b＝1
2 ；
…………10 分
同理：OQ＝OP＝1
2 ，∴Q（0， 1
），
2
此时 b＝ 1
，
2
若 d（W，△ABC）≤1，则 1
≤ b ≤1
2
…………12 分
2 ．
…………13 分
答：若 d（W，△ABC）≤1，b的取值范围是 1
≤ b ≤1
2
2 ．
26．（15 分）
（1）证明：
∵折叠，∴∠ACB=∠ACE，BC=EC，
四边形 ABCD 是平行四边形，
， //AD BC ．
AD BC
EC AD
， ACB
CAD
，
，
CAD
OA OC
，
OD OE
，
OED
ACE
ODE
OED
；
ACE
ODE
AOE
AOE
ACE
//AC DE
（2）解：∵平行四边形 ABCD 中，
四边形 ABCD 是矩形，
，
，
CAD
OED
2
2
，
ACE
OED
………………………………5 分
90
，
B
CDO
90
，
CD AB
，
3
AD BC
，
6
与（1）同理可得，OA=OC，
设OA OC x
，则
OD
6
，
x
在 Rt OCD
中，由勾股定理得：
( 3)
2
( 6
2
)x
解得：
x
3 6
4
，
2
，
x
OA CD
1 3 6
4
2
3
9 2
8
；…………10 分
90
时，延长 EA 交 BC 于 G，
，
OA
3 6
4
的面积 1
OAC
2
（3）分两种情况：
EAD
，
EAD
90
，
①如图 3，当
/ /
AD BC
EGC
AGB
30
B
，
90
，
AB
2 3
，
∴
AG ，
AEC
1
2
3
BG
B
1
2
3
30
BC
EC
GC
，
，
…………12 分
时，
2
BC
90
∴G 是 BC 的中点，
6
BG
；
AED
②如图 4，当
与（1）同理可得 //AC DE ，
CAE
CAE
∵折叠，
CAB
AED
90
，
CAE
180
90
∴
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
