人工智能答案.doc-资料库

qq_40313086-10744222-4744300845405508200.doc.pdf-第1页.png

第1页 / 共13页

qq_40313086-10744222-4744300845405508200.doc.pdf-第2页.png

第2页 / 共13页

qq_40313086-10744222-4744300845405508200.doc.pdf-第3页.png

第3页 / 共13页

qq_40313086-10744222-4744300845405508200.doc.pdf-第4页.png

第4页 / 共13页

qq_40313086-10744222-4744300845405508200.doc.pdf-第5页.png

第5页 / 共13页

qq_40313086-10744222-4744300845405508200.doc.pdf-第6页.png

第6页 / 共13页

qq_40313086-10744222-4744300845405508200.doc.pdf-第7页.png

第7页 / 共13页

qq_40313086-10744222-4744300845405508200.doc.pdf-第8页.png

第8页 / 共13页

第二章 2.8 设有如下语句，请用相应的谓词公式分别把他们表示出来： (1) 有的人喜欢梅花，有的人喜欢菊花，有的人既喜欢梅花又喜欢菊花。解：定义谓词 P(x)：x 是人 L(x,y)：x 喜欢 y 其中，y 的个体域是{梅花，菊花}。将知识用谓词表示为： ( x )(P(x)→L(x, 梅花)∨L(x, 菊花)∨L(x, 梅花)∧L(x, 菊花)) (2) 有人每天下午都去打篮球。解：定义谓词 P(x)：x 是人 B(x)：x 打篮球 A(y)：y 是下午将知识用谓词表示为： ( x )( y) (A(y)→B(x)∧P(x)) (3) 新型计算机速度又快，存储容量又大。解：定义谓词 NC(x)：x 是新型计算机 F(x)：x 速度快 B(x)：x 容量大将知识用谓词表示为： ( x) (NC(x)→F(x)∧B(x)) (4) 不是每个计算机系的学生都喜欢在计算机上编程序。解：定义谓词 S(x)：x 是计算机系学生 L(x, pragramming)：x 喜欢编程序 U(x,computer)：x 使用计算机将知识用谓词表示为： ¬ ( x) (S(x)→L(x, pragramming)∧U(x,computer)) (5) 凡是喜欢编程序的人都喜欢计算机。解：定义谓词 P(x)：x 是人 L(x, y)：x 喜欢 y 将知识用谓词表示为： ( x) (P(x)∧L(x,pragramming)→L(x, computer)) 2.10 用谓词表示法求解农夫、狼、山羊、白菜问题。农夫、狼、山羊、白菜全部放在一条河的左岸，现在要把他们全部送到河的右岸去，农夫有一条船，过河时，除农夫外船上至多能载狼、山羊、白菜中的一种。狼要吃山羊，山羊要吃白菜，除非农夫在那里。似规划出一个确 1

保全部安全过河的计划。请写出所用谓词的定义，并给出每个谓词的功能及变量的个体域。解：(1) 先定义描述状态的谓词要描述这个问题，需要能够说明农夫、狼、羊、白菜和船在什么位置，为简化问题表示，取消船在河中行驶的状态，只描述左岸和右岸的状态。并且，由于左岸和右岸的状态互补，因此可仅对左岸或右岸的状态做直接描述。本题选择对左岸进行直接描述的方法，即定义谓词如下： AL(x)：x 在左岸其中，x 的个体域是{农夫，船，狼，羊，白菜}。对应地，¬AL(x)表示 x 在右岸。问题的初始状态： AL(农夫) AL(船) AL(狼) AL(羊) AL(白菜) 问题的目标状态： ¬AL(农夫) ¬AL(船) ¬AL(狼) ¬AL(羊) ¬AL(白菜) (2) 再定义描述操作的谓词本题需要以下 4 个描述操作的谓词： L-R：农夫自己划船从左岸到右岸 L-R(x)：农夫带着 x 划船从左岸到右岸 R-L：农夫自己划船从右岸到左岸 R-L(x) ：农夫带着 x 划船从右岸到左岸其中，x 的个体域是{狼，羊，白菜}。对上述每个操作，都包括条件和动作两部分。它们对应的条件和动作如下： L-R：农夫划船从左岸到右岸条件：AL(船)，AL(农夫)，¬AL(狼)∨¬AL(羊)，¬AL(羊)∨¬AL(白菜) 动作：删除表：AL(船)，AL(农夫) 添加表：¬AL(船)，¬AL(农夫) L-R(狼)：农夫带着狼划船从左岸到右岸条件：AL(船)，AL(农夫)，AL(狼)，¬AL(羊) 动作：删除表：AL(船)，AL(农夫)，AL(狼) 添加表：¬AL(船)，¬AL(农夫)，¬AL(狼) L-R(羊)：农夫带着羊划船从左岸到右岸条件：AL(船)，AL(农夫)，AL(羊)， AL(狼)，AL(白菜) 或：AL(船)，AL(农夫)，AL(羊)，¬AL(狼)，¬AL(白菜) 动作：删除表：AL(船)，AL(农夫)，AL(羊) 2

添加表：¬AL(船)，¬AL(农夫)，¬AL(羊) L-R(白菜)：农夫带着白菜划船从左岸到右岸条件：AL(船)，AL(农夫)，AL(白菜)，¬AL(狼) 动作：删除表：AL(船)，AL(农夫)，AL(白菜) 添加表：¬AL(船)，¬AL(农夫)，¬AL(白菜) R-L：农夫划船从右岸到左岸条件：¬AL(船)，¬AL(农夫)，AL(狼)∨AL(羊)，AL(羊)∨AL(白菜) 或：¬AL(船)，¬AL(农夫) ，¬AL(狼)，¬AL(白菜)，AL(羊) 动作：删除表：¬AL(船)，¬AL(农夫) 添加表：AL(船)，AL(农夫) R-L(羊) ：农夫带着羊划船从右岸到左岸条件：¬AL(船)，¬AL(农夫)，¬AL(羊) ，¬AL(狼)，¬AL(羊)，AL(白菜) 动作：删除表：¬AL(船)，¬AL(农夫)，¬AL(羊) 添加表：AL(船)，AL(农夫)，AL(羊) (3) 问题求解过程 AL(农夫) AL(船) AL(狼) AL(羊) AL(白菜) L-R(羊) L-R(白菜) AL(农夫) AL(船) AL(羊) AL(白菜) ¬AL(狼) AL(狼) AL(白菜) ¬AL(农夫) ¬AL(船) ¬AL(羊) AL(羊) ¬AL(农夫) ¬AL(船) ¬AL(白菜) ¬AL(狼) R-L R-L R-L(羊) L-R(狼) L-R(羊) AL(农夫) AL(船) AL(狼) AL(白菜) ¬AL(羊) AL(农夫) AL(船) AL(羊) ¬AL(白菜) ¬AL(狼) AL(白菜) ¬AL(农夫) ¬AL(船) ¬AL(狼) ¬AL(羊) ¬AL(农夫) ¬AL(船) ¬AL(羊) ¬AL(白菜) ¬AL(狼) 2.18 请对下列命题分别写出它们的语义网络： (1) 每个学生都有一台计算机。解： GS GS GS 学生占有权计算机 g g g F  ISA Owner s AKO Owns o ISA c 3

(2) 高老师从 3 月到 7 月给计算机系学生讲《计算机网络》课。解： ISA 老师高老师 7 月 8 月 Start Subject Action 讲课事件 End Object Caurse 讲课计算机网络计算机系学生 (3) 学习班的学员有男、有女、有研究生、有本科生。解：参例 2.14 (4) 创新公司在科海大街 56 号，刘洋是该公司的经理，他 32 岁、硕士学位。解：参例 2.10 (5) 红队与蓝队进行足球比赛，最后以 3：2 的比分结束。解： Participants1 红队比赛 AKO 足球赛 Outcome 3:2 Participants 2 蓝队 2.19 请把下列命题用一个语义网络表示出来： (1) 树和草都是植物；解：植物 AKO 树 AKO 草 (2) 树和草都有叶和根； 4

解：叶 Have 根 Have 植物是一种是一种树草 (3) 水草是草，且生长在水中；解： AKO AKO 水草草 Live 水中植物 (4) 果树是树，且会结果；解： AKO AKO 果树 Can 树结果植物 (5) 梨树是果树中的一种，它会结梨。解： AKO AKO 树果树梨树 Can 结梨 2.26 按“师生框架”、“教师框架”、“学生框架”的形式写出一个框架系统的描述。解：师生框架 Frame Name：Unit（Last-name，First-name） Sex：Area（male，female） Default：male Age：Unit（Years） Telephone：Home Unit（Number） Mobile Unit（Number）教师框架 Frame AKO Major：Unit（Major-Name） Lectures：Unit（Course-Name） 5

Field：Unit（Field-Name） Project ：Area（National，Provincial，Other） Default：Provincial Paper：Area（SCI，EI，Core，General） Default：Core 学生框架 Frame AKO< Teachers-Students > Major：Unit（Major-Name） Classes：Unit（Classes-Name） Degree：Area（doctor，mastor, bachelor） Default：bachelor 2.37 把下列谓词公式化为子句集（1) (x)(y)(P(x, y)∧Q(x, y)) (2) (x)(y)(P(x, y)→Q(x, y)) (3) (x)(y)(P(x, y)∨(Q(x, y)→R(x, y))) (4) (x) (y) (z)(P(x, y)→Q(x, y)∨R(x, z)) 解：(1) 由于(x)(y)(P(x, y)∧Q(x, y))已经是 Skolem 标准型，且 P(x, y)∧Q(x, y)已经是合取范式，所以可直接消去全称量词、合取词，得 { P(x, y), Q(x, y)} 再进行变元换名得子句集： S={ P(x, y), Q(u, v)} (2) 对谓词公式(x)(y)(P(x, y)→Q(x, y))，先消去连接词“→”得： (x)(y)(¬P(x, y)∨Q(x, y)) 此公式已为 Skolem 标准型。再消去全称量词得子句集： S={¬P(x, y)∨Q(x, y)} (3) 对谓词公式(x)(y)(P(x, y)∨(Q(x, y)→R(x, y)))，先消去连接词“→”得： (x)(y)(P(x, y)∨(¬Q(x, y)∨R(x, y))) 此公式已为前束范式。再消去存在量词，即用 Skolem 函数 f(x)替换 y 得： (x)(P(x, f(x))∨¬Q(x, f(x))∨R(x, f(x))) 此公式已为 Skolem 标准型。最后消去全称量词得子句集： S={P(x, f(x))∨¬Q(x, f(x))∨R(x, f(x))} (4) 对谓词(x) (y) (z)(P(x, y)→Q(x, y)∨R(x, z))，先消去连接词“→”得： 6

(x) (y) (z)(¬P(x, y)∨Q(x, y)∨R(x, z)) 再消去存在量词，即用 Skolem 函数 f(x)替换 y 得： (x) (y) (¬P(x, y)∨Q(x, y)∨R(x, f(x,y))) 此公式已为 Skolem 标准型。最后消去全称量词得子句集： S={¬P(x, y)∨Q(x, y)∨R(x, f(x,y))} 2.41 设已知： (1) 如果 x 是 y 的父亲，y 是 z 的父亲，则 x 是 z 的祖父； (2) 每个人都有一个父亲。使用归结演绎推理证明：对于某人 u，一定存在一个人 v，v 是 u 的祖父。解：先定义谓词 F(x,y)：x 是 y 的父亲 GF(x,z)：x 是 z 的祖父 P(x)：x 是一个人再用谓词把问题描述出来：已知 F1：(  x) ( y) ( z)( F(x,y)∧F(y,z))→GF(x,z)) F2：( y)(P(x)→F(x,y)) 求证结论 G：(  u) ( v)( P(u)→GF(v,u)) 然后再将 F1，F2 和¬G 化成子句集： ① ¬F(x,y)∨¬F(y,z)∨GF(x,z) ② ¬P(r)∨F(s,r) ③ P(u) ④ ¬GF(v,u)) 对上述扩充的子句集，其归结推理过程如下： ¬F(x,y)∨¬F(y,z)∨GF(x,z) ¬GF(v,u) ¬F(x,y)∨¬F(y,z) ¬P(r)∨F(s,r) ¬F(y,z)∨¬P(y) ¬P(r)∨F(s,r) ¬P(y)∨¬P(z) ¬P(y) P(u) 7 NIL

由于导出了空子句，故结论得证。 2.42 假设张被盗，公安局派出 5 个人去调查。案情分析时，贞察员 A 说：“赵与钱中至少有一个人作案”，贞察员 B 说：“钱与孙中至少有一个人作案”，贞察员 C 说：“孙与李中至少有一个人作案”，贞察员 D 说：“赵与孙中至少有一个人与此案无关”，贞察员 E 说：“钱与李中至少有一个人与此案无关”。如果这 5 个侦察员的话都是可信的，使用归结演绎推理求出谁是盗窃犯。解：(1) 先定义谓词和常量设 C(x)表示 x 作案，Z 表示赵，Q 表示钱，S 表示孙，L 表示李 (2) 将已知事实用谓词公式表示出来赵与钱中至少有一个人作案：C(Z)∨C(Q) 钱与孙中至少有一个人作案：C(Q)∨C(S) 孙与李中至少有一个人作案：C(S)∨C(L) 赵与孙中至少有一个人与此案无关：¬ (C (Z)∧C(S))，即 ¬C (Z) ∨¬C(S) 钱与李中至少有一个人与此案无关：¬ (C (Q)∧C(L))，即 ¬C (Q) ∨¬C(L) (3) 将所要求的问题用谓词公式表示出来，并与其否定取析取。设作案者为 u，则要求的结论是 C(u)。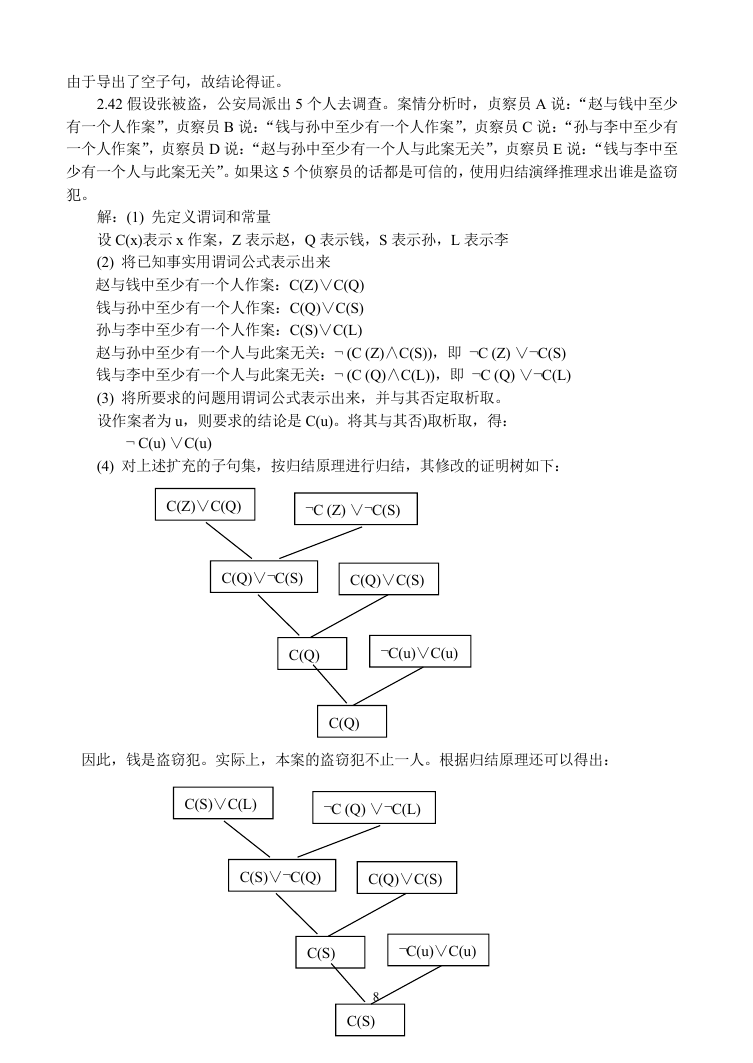将其与其否)取析取，得： ¬ C(u) ∨C(u) (4) 对上述扩充的子句集，按归结原理进行归结，其修改的证明树如下： C(Z)∨C(Q) ¬C (Z) ∨¬C(S) C(Q)∨¬C(S) C(Q)∨C(S) C(Q) ¬C(u)∨C(u) C(Q) 因此，钱是盗窃犯。实际上，本案的盗窃犯不止一人。根据归结原理还可以得出： C(S)∨C(L) ¬C (Q) ∨¬C(L) C(S)∨¬C(Q) C(Q)∨C(S) C(S) ¬C(u)∨C(u) 8 C(S)

资料库

人工智能答案.doc

相关推荐

课程资源

热门标签

最新资料