logo资料库

ansoft12在工程电磁场中的应用.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：13.12M 资料格式：pdf 举报 版权申诉
第1页 / 共401页
第2页 / 共401页
第3页 / 共401页
第4页 / 共401页
第5页 / 共401页
第6页 / 共401页
第7页 / 共401页
第8页 / 共401页
资料共401页，剩余部分请下载后查看
    第一章 Ansoft 二维使用基础 本章主要介绍了 Ansoft V12 版本二维有限元软件的操作基础，Ansoft 除了计算的准确 度、快速性之外，还应该具有操作简单、使用快捷等优点，但是再好的软件也需要读者经 过一定时间学习之后才能上手。本章将二维有限元操作中的共性问题提出，希望通过对本 章的学习，能在最短的时间内上手 Ansoft V12，并对 Ansoft 有限元的流程有一定的了解。 1
    第一章 Maxwell 2D 使用基础 本章导读： Ansoft V12 有限元计算软件，在不同的计算模块中，有不同的计算侧重点，但作为有 限元软件，其计算流程和绘制模型、材料添加、后处理等操作又具有相当大程度的相似性， 所以将相似性较高的部分取出，单独成章，方便阅读和查阅，而不具备通用性的内容则尽 量在各相关章节给予说明。本章内容包括： 认识 Maxwell 2D 的界面环境 Maxwell 2D 的模型绘制 Maxwell 2D 的材料管理 Maxwell 2D 的边界条件和激励源 Maxwell 2D 的网格剖分和求解设置 Maxwell 2D 的后处理操作流程 1.1 初识 Maxwell 2D 的界面环境 Maxwell 2D 界面与上一版本相比较改动较大，基本上已经颠覆了老版本的界面和操作 方式，所以对于部分软件的老用户来讲，需要从新熟悉新版本的操作。因此，本章先介绍 一下操作界面，如图 1-1 所示的是 Maxwell 2D 的操作界面，在菜单工具栏下，主要有 6 个 工作区域。 图 1-1 Maxwell V12 2D 操作界面 2
    左侧为工程管理栏，可以管理一个工程文件中的不同部分或管理几个工程文件。其下 方为工程状态栏，在对某一物体或属性操作时，可在此看到操作的信息。最下方并排的是 工程信息栏，该栏显示工程文件在操作时的一些详细信息，例如警告提示，错误提示，求 解完成等信息。在旁边的工程进度栏内主要显示的是求解进度，参数化计算进度等，该进 度信息通常会用红色进度条表示完成的百分比。在屏幕中部是工程树栏，在此可以看到模 型中的各个部件及材料属性、坐标系统等关键信息，也方便用户对其进行分别管理。在操 作界面最右侧较大区域为工程绘图区，用户可以在此绘制所要计算的模型，也可以在此显 示计算后的场图结果和数据曲线等信息。绘图时带有笛卡尔坐标系和绘图网格，方便用户 绘制模型。 如果读者不小心在操作中将这几区域给关闭了，还可以在 View 菜单栏中将其对应项 前的对号勾上，则对应的区域会从新显示出来。如图 1-2 所示。 图 1-2 View 菜单下恢复操作区域 在界面的主菜单下，有两至三排的快捷按钮，现将主要操作按钮介绍一下。 (1) 计算类型快捷按钮 (2) 常用快捷按钮 (3) 视图操作快捷按钮 (4) 模型绘制快捷按钮 (5) 模型材料快捷按钮 (6) 相对坐标系快捷按钮 3
    (7) 模型检测和注释快捷按钮 图 1-3 Maxwell V12 2D 主要操作按钮 当然，还有其他一些未说明的操作按钮，在不同操作状态下软件会自动显示可以使用 的操作按钮，而不可使用的功能操作按钮则会显示为灰色。这些快捷按钮在下拉菜单栏中 都有相应的位置，也可以通过下拉菜单进行操作。 在图 1-3 (1)中的三个图标，从左至右分别为新建 Maxwell 2D 工程，新建 RMxprt 工程 和新建 Maxwell 3D 工程。 图 1-3 (2)中的则是常用快捷按钮，有新建、打开、保存和打印等常用功能按钮。 图 1-3 (3)中则是常用视图操作按钮，有视图移动、旋转、缩放和全局视图等按钮。 图 1-3 (4)中所示的是常用绘图按钮，分为常用绘制线段、曲线、圆、圆弧和函数曲线 按钮，以及常用绘制面的按钮，分为矩形面、圆面、正多边形面和椭圆面几个快捷按钮。 图 1-3 (5)是材料快捷按钮，在绘制模型前，可以点击下拉菜单事先选择好所绘模型的 材料，方便按照材料进行模型绘制分组，软件默认的是真空材料。 图 1-3 (6)是相对坐标系快捷按钮，对于永磁体充磁和特殊几何模型绘制时需要采用局 部坐标系，通过使用快捷按钮可以将坐标系移动和旋转，从而生成新的局部坐标系。 图 1-3 (7)是模型检测，求解和书写注释等按钮。在求解模型前，建议用户要先检测一 下模型，看是否有错误和警告，以便在求解前排除问题，此外，还可以对所计算的模型书 写备忘录，在大批量计算近似模型时，书写备忘录是个很不错的选择，方便用户查找和记 录工程之间的差别。 图 1-4 Maxwell V12 帮助菜单 好的软件都具备一套完善的帮助文档，Maxwell V12 也是这样，鼠标左键点击在主界 4
    面的 Help 菜单下的 Comtents 项或直接在键盘上按下 F1 键，软件会自动弹出如图 1-4 所示 的实时帮助文档，该文档不仅包括了 2D 内容，还有 RMxprt 和 Maxwell 3D 两部分的帮助 文档。对于新用户来讲，这个帮助文档是最好的培训教材，建议用户熟悉该文档的结构和 相关内容。同时该帮助文档还支持关键词查询和索引等检索方式，也大大减少了用户花费 在查询上的时间。 1.2 Maxwell 2D 的模型绘制 在 2D 的新版本的绘图部分已经更改了许多地方，这也需要用户花费更多的时间来熟 悉和适应新版本的模型绘制体系。绘制二维模型时，可以采用快捷按钮绘图，也可以采用 下拉菜单绘制，两者的效果是相同的，在图 1-5 中所示 图 1-5 Maxwell V12 绘图菜单 在图 1-5 所示的绘图菜单栏中，自上而下分别为绘制线段、绘制曲线、绘制圆弧和绘 制函数曲线；绘制矩形面、绘制椭圆面、绘制圆面和绘制正多边形面域；沿路径扫描，插 入已有模型；绘制面、绘制点；插入多段线等操作选项，最后灰色的按钮是创建域，多用 来绘制求解域等。 在讲解模型绘制前，需要事先介绍软件的默认坐标系和模型绘制方式。图 1-6 所示的 是在屏幕右下角的模型绘制坐标系，无论绘制线段还是圆弧，都可以在此对话框中输入所 给定的坐标，因为软件采用的是 2D 和 3D 在同一个绘图区，所以在绘制 2D 模型时 Z 方向 上的量可以恒定为 0，仅输入 X 和 Y 方向上的坐标数据即可。在三个方向上数据栏后有两 个下拉菜单，第一个为绘制模型时的坐标，默认是采用 Absolut 绝对坐标，也可以通过下 拉菜单将其更换为相对坐标，则后一个操作会认为前一个绘图操作的结束点为新相对坐标 点起点。后一个下拉菜单是坐标系统的选择，共有三种常用坐标系统，分别是 Cartesiar 直 角坐标系，Cylindrical 柱坐标系和 Spherical 球坐标系。当绘制的模型形状不一时，可以根 据其需要更换不同的坐标系。软件默认的是直角坐标系。 图 1-6 Maxwell V12 模型绘制坐标系 5
    1.2.1 曲线模型的绘制 在绘制曲线模型时，系统默认的是将封闭后的曲线自动生成面，如果用户不想让其自 动生成面，可以在绘制曲线模型前，点击菜单栏中的 Tools/Options/Modeler Options 项更改 绘图设置，如图 1-7 所示。单击 Modeler Options 后，会自动弹出如图 1-8 所示的界面。 图 1-7 模型绘制选项 图 1-8 模型绘制选项卡 在 Operation，Display，Drawing 三个选项中，选择第一 Operation 选项，并将 Polyline 项下默认的 Autimatically cover closed polyline 项前的对号去掉，去掉对号后，单击确定按 钮退出，系统将不再对封闭的曲线强制生成面了。在后续的绘图操作中，很多地方都需要 事先将该选项屏蔽掉，还请读者对此多多留意。 例 1-1：在 2D 中的 XOY 平面内绘制正四边形，边长等于 10 mm，起点坐标为原点(0， 0，0)，正四边形位于第一象限内。 首先点击快捷按钮 ，新建一个 Maxwell 2D 工程文件，在点击绘制线段快捷按钮 ， 或在菜单栏中选择 Draw/Line。在屏幕右下角的坐标栏内输入起点坐标 X=0，Y=0，Z=0 并 点击键盘上的 Enter 键确认，再输入下一个顶点坐标 X=10，Y=0，Z=0，单击回车确认， 继续输入第三个顶点坐标顶点 X=10，Y=10，Z=0，并回车确认；再次输入第四个顶点坐标 X=0，Y=10，Z=0，同时回车确认该点坐标，至此已经绘制完毕正四边形的三条边，最后 再次输入坐标 X=0，Y=0，Z=0，点击回车确认后即可封闭曲线。整个流程如图 1-9 所示。 （1）正四边形起点输入坐标 （2）正四边形第二顶点输入坐标 （3）正四边形第三顶点输入坐标 （4）正四边形第四顶点输入坐标 （5）正四边形封闭时输入坐标 图 1-9 正四边形绘制流程中各点坐标值 6
    (1) 不选择自动生成面时的效果 (2) 选择自动生成面时的效果 图 1-10 正四边形绘制完毕后的图形 从图 1-10 中可以看出，在采用自动生成面功能后，直接绘制正四边形的四条线段就可 以自动形成正四边形面域。 因为生成圆弧、整圆、样条曲线的方式与例 1 中的操作相似，都可以通过逐次输入关 键点坐标实现，所以在此不做过多的叙述。 例 1-2：在 2D 中的 XOY 平面内绘制三叶玫瑰线，不使封闭曲线生成面域。 既然不让自动闭合的曲线形成面，那么仍需要在 Tools/Options/Modeler Options 中去掉 Polyline 项下默认的 Autimatically cover closed polyline 前的对号。同时由于三叶玫瑰线形状 较为复杂，采用直线或圆弧等操作无法准确绘制，所以在此使用了函数绘制方式，而该绘 制曲线方式对将来复杂模型处理极为方便快捷，故特别将其提出作为案例详细加以说明。 假设需要绘制的三叶玫瑰线曲线参数方程如下： tx )( ty )( = = 10 10 ⋅ ⋅ sin( sin( t )3 t )3 ⋅ ⋅ t cos( t sin( ) ) ⎧ ⎨ ⎩ π≤≤ t0 很明显，如此复杂的形状不可能使用简单的曲线绘制方法实现，在其他商业有限元软 件中多数都是通过转换其他 CAD 软件曲线图实现。而在 Maxwell 中可以通过采用参数绘 制方式实现，非常方便。 首先，在快捷按钮中点击 按钮，或者在菜单栏中单击 Draw/Equation Based Curve 选 项，系统会自动弹出参数曲线绘制窗口，如图 1-11 所示。 图 1-11 参数曲线绘制窗口 从上图可以看出，软件默认的参数变量为_t，在 X、Y、Z 三个方向上都可以设置为_t 的函数，而在 Start_t 和 End_t 中设置参数_t 的起始和终止范围，通过 Points 项可以设置由 2
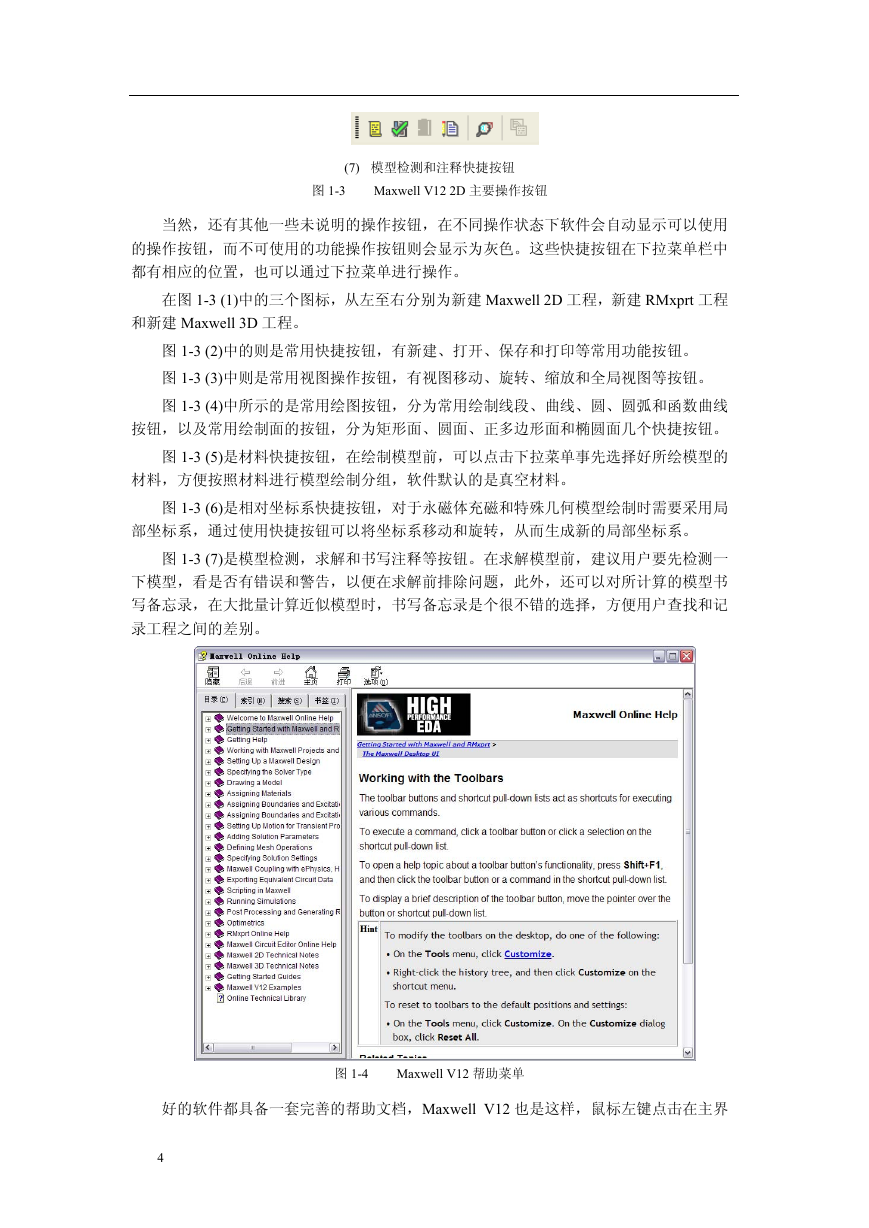
    多少个点组成该参数曲线，若设置为 0 则表示由软件默认的点数组成，此时的曲线较为光 滑，若该项设置过少则曲线将有多段直线组成。 点击图 1-11 中 X(_t)项后的 按钮，则会弹出如图 1-12 所示界面。 图 1-12 参数曲线绘制窗口 在上图中 X(t)=项后一栏为 X 方向参数方程输入栏，可以在此直接输入关于_t 的参数 方程。Insert Function 项是输入系统自带的内置函数，点击右侧的下拉箭头就可以看到非常 丰富的内置函数，包括三角函数、反三角函数、取绝对值、求余、指数和对数等，基本满 足常用计算需求。在下拉菜单里选择相应的函数，然后再点击 Insert Function 按钮就可以 直接将内置函数填入参数方程栏内，当然如果用户对软件非常熟悉的话，也可以自行在参 数方程栏中写入所需函数。Insert Operator 项是插入数学运算和逻辑操作，在该下拉菜单中 包括常用的与、或、非、点乘、叉乘等操作，同样先点击右侧的箭头，在从中选择相应的 数学操作，然后单击 Insert Operator 按钮即可。Insert Quantity 项是插入参数项，系统默认 的参数名称为_t。 在此分别在 X 向参数方程表达式中写入 10*sin(3*_t)*cos(_t)，并点击 OK 按钮退出设 定界面。 与之相似的是 Y(_t)项，点击图 1-11 中 Y(_t)栏后的 按钮，在弹出的 Y 方向参数方 程对话框中输入 10*sin(3*_t)*sin(_t)并点击 OK 退出设定窗口。 由于需要在 XOY 平面内绘制三叶玫瑰线，所以在 Z 方向上可以设定为 Y(_t)=0。同时， 参数_t 的初始值设定为 0，而终止值设定为 3.14159265，即实现在 0 度至π弧度内绘制曲 线。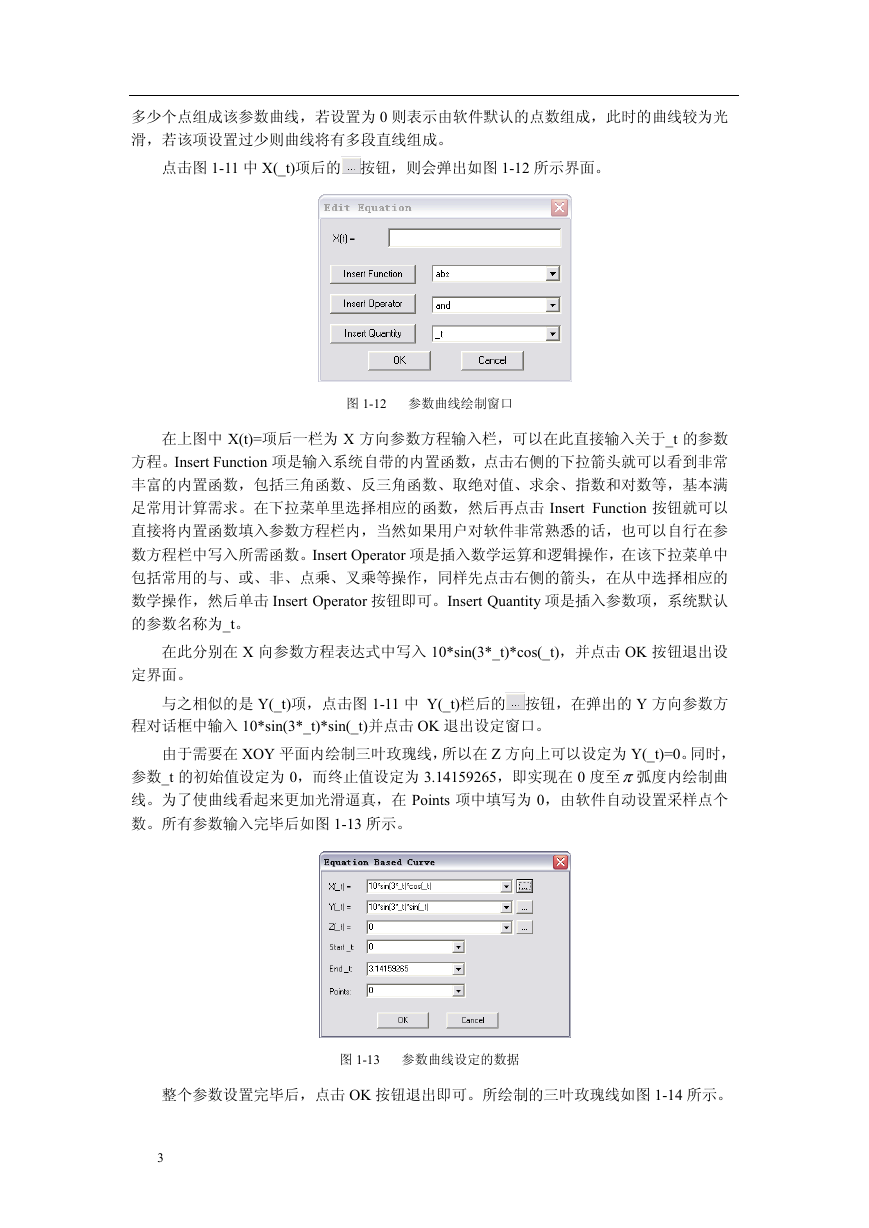为了使曲线看起来更加光滑逼真，在 Points 项中填写为 0，由软件自动设置采样点个 数。所有参数输入完毕后如图 1-13 所示。 图 1-13 参数曲线设定的数据 整个参数设置完毕后，点击 OK 按钮退出即可。所绘制的三叶玫瑰线如图 1-14 所示。 3
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料