logo资料库

n皇后问题论文.docx

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.22M 资料格式：docx 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    n皇后问题
    摘要
    1.介绍
    2.n后问题的解决
    2.1问题分析
    2.2算法设计
    2.3程序流程图
    2.4算法的时间复杂度
    2.5可行解的检测
    2.6可行解的规律
    3.开发环境
    4.总结
    参考文献
    附录
    n 皇后问题 摘要 n 皇后问题要求在一个 n×n 格的棋盘上放置彼此的不受攻击的 n 个皇后。 按照国际象棋的规则，皇后可以攻击与之处于同一行或同一列或同一斜线上的棋 子。n 后问题等价于在 n×n 格的棋盘上放置 n 个皇后，任何 2 个皇后不放在同 一行或同一列或同一斜线上。 本篇论文主要是从回溯的角度用 c 语言作为平台来解决 n 皇后问题。利用递 归函数，按深度优先策略，从根节点出发对整个解空间进行回溯搜索，并在搜索 过程中用剪枝函数避免无效搜索，找出满足约束条件的解决方案。使用回溯算法 最终不仅能使问题变得一目了然，更加易懂，还提高了寻找可行解的效率(相对 于穷举法)。 关键词：皇后问题，c 语言，回溯法，深度优先 1. 介绍 八皇后问题最早是由国际西洋棋棋手马克斯•贝瑟尔于 1848 年提出。之后陆 续有数学家对其进行研究，其中包括高斯和康托，并且将其推广为更一般的 n 皇后摆放问题。八皇后问题的第一个解是在 1850 年由弗朗兹•诺克给出的。诺克 也是首先将问题推广到更一般的 n 皇后摆放问题的人之一。1874 年，S.冈德尔提 出了一个通过行列式来求解的方法，这个方法后来又被 J.W.L.格莱舍加以改进。 艾兹格•迪杰斯特拉在 1972 年用这个问题为例来说明他所谓结构性编程的能力。 八皇后问题推广为更一般的 n 皇后摆放问题时，棋盘的大小变为 n×n，而皇后 个数也变成 n。当且仅当 n = 1 或 n ≥ 4 时问题有解。 以八皇后的摆放为背景，高斯认为有 76 种方案。1854 年在柏林的象棋杂志 上不同的作者发表了 40 种不同的解，后来有人用图论的方法解出 92 种结果。计 算机发明后，有多种方法可以解决此问题，其中包括递归算法、非递归算法、迭 代算法和回溯法。 递归算法写出来的代码思路清晰，可读性强，并且由于递归算法用一个函数 通过不断对自己的调用而求得最终结果，所以程序比较短；但，递归的函数调用 是有开销的，而且递归的次数受堆栈大小的限制，当深度过大时，算法的时空性 就不好了。 而非递归算法则通过循环语句把一些实现的细节清晰地展示在用户的面前， 所以相应的程序更长些，但它不容易理解，编写复杂问题时困难；而非递归效率
    高，运行时间只因循环次数增加而增加，没有额外开销。 迭代法利用计算机运算速度快、适合做重复性操做的特点，让计算机对一组 指令(或一定步骤)进行重复执行，在每次执行这组指令(或这些步骤)时，都从变 量的原值推出它的一个新值。最重要的是，该问题一定有解；若无解，就成了死 循环。如当 n=2 时，程序就死了。 最后，回溯法则是小组讨论所用的算法，在后面将要进行讲解。 所以，当比较多个算法时，还要看 n 的取值。 2. n 后问题的解决 本篇论文为了能够更好的展示出 n 皇后的算法思想，因此在以下的算法设 计讲解中，图形中会将 n 皇后具体化为八皇后。这样即方便讲解也方便了读者理 解皇后问题的解决过程。 n 皇后问题的程序的功能主要有是能够改变皇后的个数即棋盘规格、快速 查找并显示八皇后的布局方式和可行方案的个数。 2.1 问题分析 由于是在 n×n 的棋盘中放置 n 颗棋子，使他们满足任何 2 个不在同一行或 同一列或同一斜线上，那么可以将问题简化：将 n 颗棋子分别固定放在 n 行上， 每列一颗棋子，这样它们才符合在不同行上，同时对每行上的棋子进行摆放，使 其不在同一列或同一斜线上。从每一行的第一列开始摆放棋子，第一行开始，再 依次的摆放第二行第一列、第三行第一列等，当当前所在列不符合要求时，换下 一列，直至符合，若此列结束，则将上一行的棋子移至下一列，再继续以后行的 棋子摆放，当第 n 个皇后放置成功后，即得到一个可行解，此时再回到上一个皇 后重新放置寻找下一个可行解，直至第一行的棋子摆放到最后一列时，不能再继 续向下一列移动，此时，所有可行解就已经找出。 2.2 算法设计 用 n 元组 x[1:n]表示 n 后问题的解。其中，x[i]表示皇后 i 放在棋盘上的第 i 行的第 x[i]列。根据 n 皇后问题的要求，它们必须满足的约束条件是： [ ] x i  [ ] x i  i       [ ] , x j i [ ] x j j  j  1,2..., n i 且  j (1) 1 , i j  1,2..., n i 且  j (2) (1) 式则代表 i 行和 j 行不在同一列上，而(2)式代表 i 行和 j 行不在同一斜线上。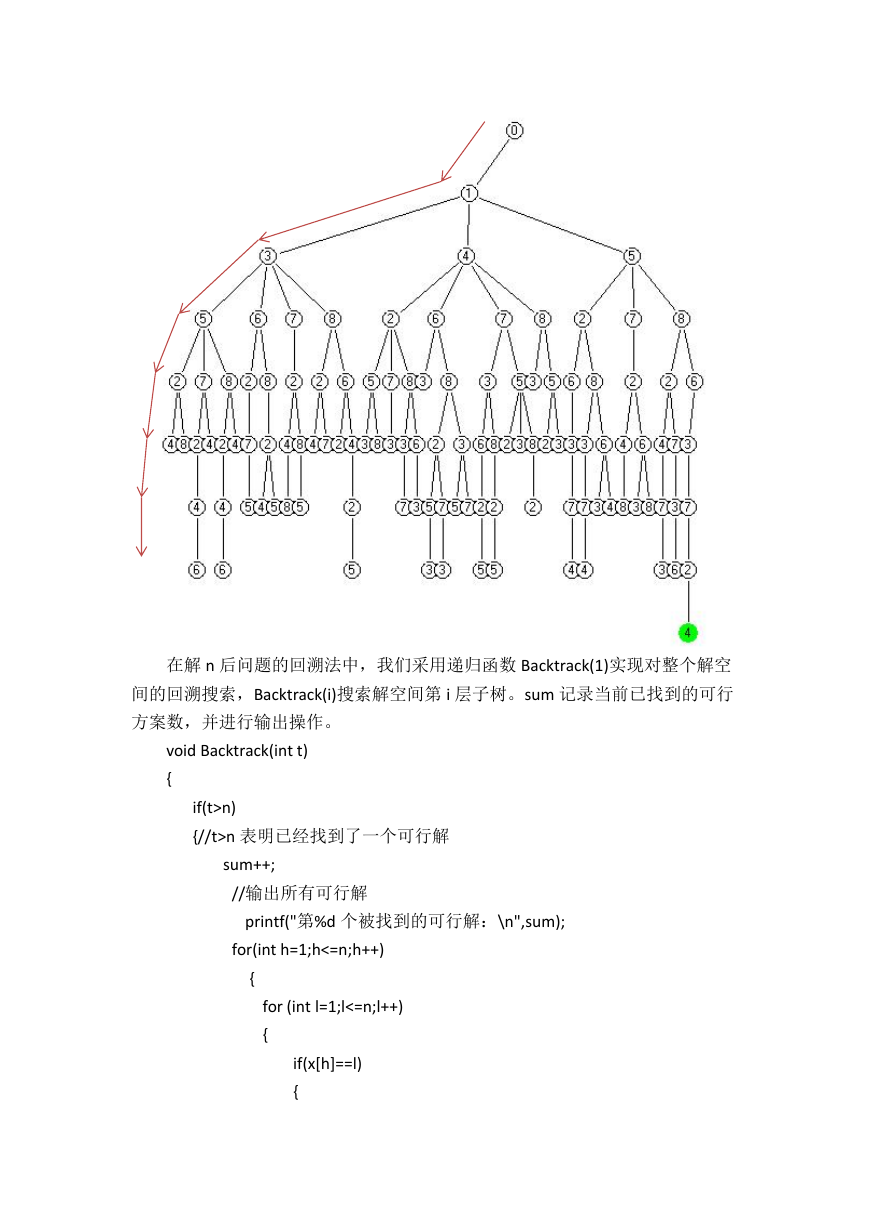 在我们用回溯法解决 n 后问题时，用完全 n 叉树表示解空间。我们用二维表 格表示棋盘，从 1 开始算起，下图为当第 1 行的第 1 列摆放棋子时的部分解的寻 找过程。
    在解 n 后问题的回溯法中，我们采用递归函数 Backtrack(1)实现对整个解空 间的回溯搜索，Backtrack(i)搜索解空间第 i 层子树。sum 记录当前已找到的可行 方案数，并进行输出操作。 void Backtrack(int t) { if(t>n) {//t>n 表明已经找到了一个可行解 sum++; //输出所有可行解 printf("第%d 个被找到的可行解：\n",sum); for(int h=1;h<=n;h++) { for (int l=1;l<=n;l++) { if(x[h]==l) {
    printf("1 "); printf("0 "); } else { } } } printf("\n"); printf("\n"); }else { for(int i=1;i<=n;i++) { x[t]=i; if(Place(t)) { Backtrack(t+1); } } } } 在 Backtrack(int t)中，Place(int k)函数用来判断当前位置是否符合约束条件， 其中 for 循环表示第 k 行的列号要与 k 之前的所有行进行比较，当都满足约束条 件时，k 行才能将棋子放在 x[k]列上。 bool Place(int k) { for (int j=1;j
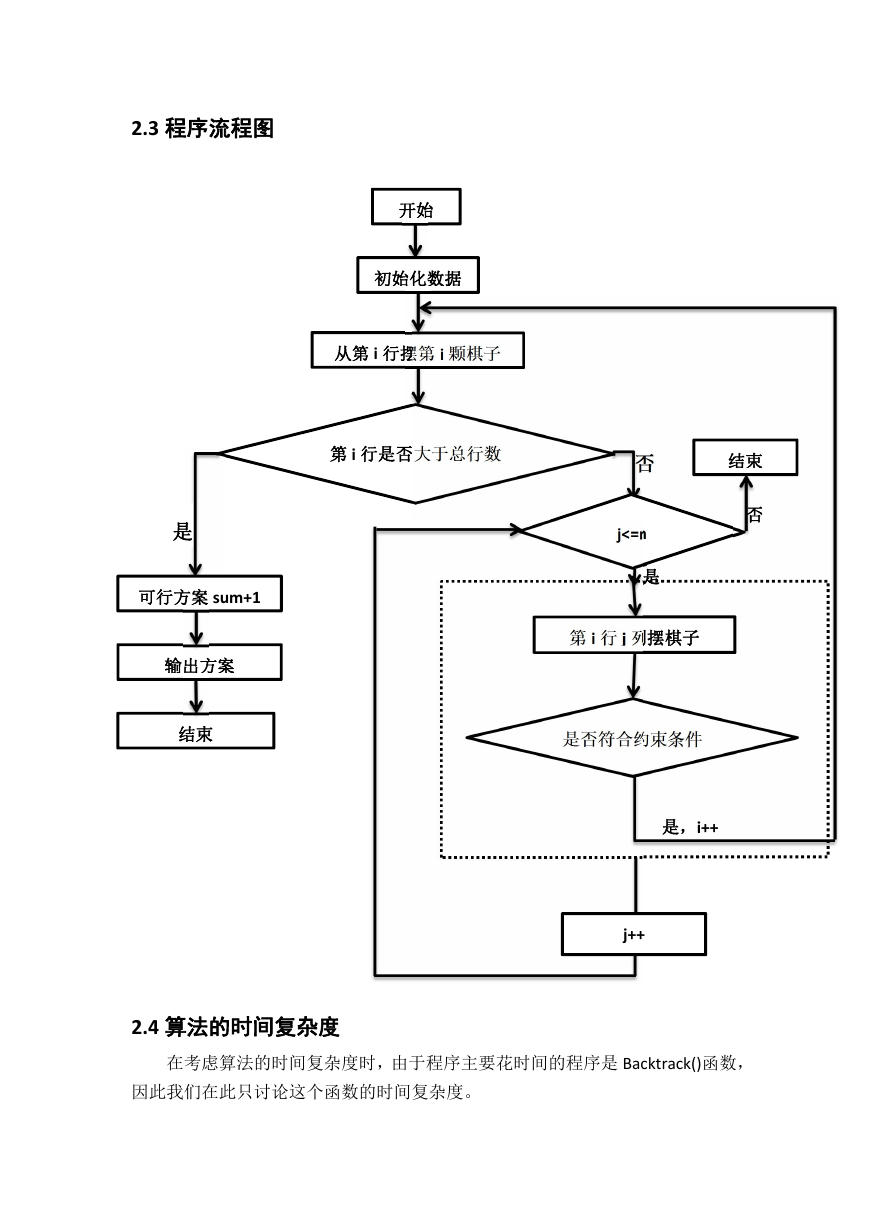
    开始 初始化数据 从第 i 行摆第 i 颗棋子 第 i 行是否大于总行数 2.3 程序流程图 是 可行方案 sum+1 输出方案 结束 结束 否 否 j<=n 是 第 i 行 j 列摆棋子 是否符合约束条件 是，i++ j++ 2.4 算法的时间复杂度 在考虑算法的时间复杂度时，由于程序主要花时间的程序是 Backtrack()函数， 因此我们在此只讨论这个函数的时间复杂度。
    在 Backtrack()函数中，有一个 for 循环，为当前行的列进行赋值，赋值后执 行 Place()函数进行判断是否满足约束条件，而在 Place()函数中又有一个 for 循环 进行检测当前行和之前所有行是否冲突，所以 Backtrack()函数的时间复杂度为 O(n^n)。 2.5 可行解的检测 八皇后问题共有 92 个可行解，那么该怎样解决可行解的检测呢？一个一个 的验证是非常繁琐的过程，若 n 的值变得更大，那么就更不方便进行可行解的检 测了。因此这里我们可以用一个随机函数: # include “time.h” srand((unsigned)time(NULL)); /*随机种子*/ n=rand()%(Y-X+1)+X; /*n 为 X~Y 之间的随机数*/ 将 X、Y 赋为皇后可行解的个数，在所有可行解中进行随机的选取，当 sum==n 时，就将此时的可行解选取出来进行验证，这样就避免了可行解的全部检测，而 且也能证明可行解的正确性。 2.6 可行解的规律 从八皇后问题的 92 个可行解中我们可以看出，可行解之间是存在着关系的， 例如，将一个可行解关于中轴线旋转 180 度（如图所示），得到的不同的棋子摆 法也将是一个可行解，因为棋子之间的相对位置并没发生改变，所以棋子也将符 合皇后问题的约束条件。同样，将棋盘关于对角线翻转、横中轴线翻转，都可以 得到不同的可行解。
    对于八皇后的 92 个解中，出去可翻转、对称的可行解外，真正的独立解只 有 12 个。 3. 开发环境 windows7 操作系统，VC++ 6.0 C 语言平台。 4. 总结 在处理 n 后这种有明确的解空间的问题时，我们都可以使用回溯法进行求解。 对于八皇后问题而言，其方法的组合数是很大的。利用显约束排除 2 个皇后在同 一行或同一列的放法，也还有 8！种不同的放法。可用算法 Estimate 来估计回溯 法中产生的节点数为 109601 个，约为总节点数的 1.55%。这就说明了回溯法的 效率大大高于穷举法。然而，在算法设计的过程中，我们并未过多的考虑到我们 所设计的程序的运行时间规模，这样便导致了程序有所冗余，运行时间有所增加。 参考文献  Watkins, John J. (2004). Across the Board: The Mathematics of Chess Problems. Princeton: Princeton University Press. ISBN 0-691-11503-6.  O.-J. Dahl, E. W. Dijkstra, C. A. R. Hoare Structured Programming, Academic Press, London, 1972 ISBN 0-12-200550-3 see pp 72-82 for Dijkstra's solution of the 8 Queens problem.  《计算机算法设计与分析》（第三版） 王晓东 编著 附录 1.n 皇后问题的详细程序如下： #include "stdio.h"
    int sum;//当前已找到的可行解 int n; //皇后个数 int x[100];//当前解 void main() { void Backtrack(int t); printf("请输入皇后个数 n:\n"); scanf("%d",&n); sum=0; Backtrack(1); printf("\n 可行解数目：%d\n",sum); } //判断此处是否可以放 bool Place(int k) { for(int j=1;jn)
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料