多振幅MSK的调制的实现.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：1.12M 资料格式：pdf 举报版权申诉

chenxinshuyu-3300601-16359647447376301042.pdf-第1页.png

第1页 / 共9页

chenxinshuyu-3300601-16359647447376301042.pdf-第2页.png

第2页 / 共9页

chenxinshuyu-3300601-16359647447376301042.pdf-第3页.png

第3页 / 共9页

chenxinshuyu-3300601-16359647447376301042.pdf-第4页.png

第4页 / 共9页

chenxinshuyu-3300601-16359647447376301042.pdf-第5页.png

第5页 / 共9页

chenxinshuyu-3300601-16359647447376301042.pdf-第6页.png

第6页 / 共9页

chenxinshuyu-3300601-16359647447376301042.pdf-第7页.png

第7页 / 共9页

chenxinshuyu-3300601-16359647447376301042.pdf-第8页.png

第8页 / 共9页

Multi-amplitude minimum shift keying modulation format for optical communications

Introduction

Multi-amplitude CPM (MACPM) and multi-amplitude MSK (MAMSK)

Optical MSK and multi-amplitude MSK transmitters

Optical MAMSK detection

Simulation results and discussions

Spectral properties and dispersion tolerance of 2-AMSK

Transmission performance

Conclusion

Acknowledgements

Appendix. Performance evaluation under multiple peaks statistical distribution [25]

References

Optics Communications 281 (2008) 4245–4253 Contents lists available at ScienceDirect Optics Communications j o u r n a l h o m e p a g e : w w w . e l s e v i e r . c o m / l o c a t e / o p t c o m Multi-amplitude minimum shift keying modulation format for optical communications Le Nguyen Binh * Centre for Telecommunications and Information Engineering, Department of Electrical and Computer Systems Engineering, Monash University, Clayton, Victoria 3168, Australia Lehrstuhl für Nachrichen- und Übertragungstechnik, Technische Fakultaet der Christian Albretchs Universitaet zu Kiel,Kaiserstraße 2, D-24143 Kiel, Germany a r t i c l e i n f o a b s t r a c t Article history: Received 14 February 2008 Received in revised form 11 April 2008 Accepted 11 April 2008 We present the multi-amplitude level minimum shift keying (M-ary MSK) modulation scheme for long haul optically ampliﬁed transmission systems. New conﬁgurations of optical M-ary MSK transmitters using two cascaded electro-optic phase modulators are proposed and its detailed operation principles are expressed. The optical receiver for optical multi-amplitude MSK modulation format requires both amplitude direct-detection and differential phase balanced-detection. Numerical results on spectral haracteristics, dispersion tolerance and the relationship between amplitude and phase with launched average power for long-haul transmission of multi-level MSK modulation format are presented. The dis- persion tolerance shows that the 2-amplitude MSK at 80 Gb/s is well compared with 40 Gb/s binary MSK modulation format. Ó 2008 Elsevier B.V. All rights reserved. 1. Introduction Recently, advanced modulation formats have attracted inten- sive research for long haul optical transmission systems including various amplitude and discrete differential phase modulation and pulse shape formats (ASK-NRZ/RZ/CSRZ, DPSK and DQPSK-NRZ/ RZ/CSRZ). For the case of phase modulation the phases of the opti- cal carrier are discretely coded with ‘‘0”, ‘‘p” (DPSK) or ‘‘0”, ‘‘p” and ‘‘p/2, p/2” (DQPSK). Although, the differential phase modulation techniques offer better spectral properties, higher energy concentration in the signal bands and more robustness to combat the non-linearity impairments as compared to the amplitude modulation formats, phase continuity would offer even better spectral efﬁciency and at least 20 dB better in the suppression of the side lobes [1]. Minimum Shift Keying (MSK), exhibits a dual alternating frequency between the two consecutive bit periods is considered to offer the best scheme as this offers orthogonal property of the two- frequency modulation of the carrier lightwaves embedded within the consecutive bits. Furthermore it offers the most simplicity in the implementation of the modulation in the photonic domain. Single level MSK has been extensive investigated [2–4,8,9] but there are no published works on multi-level or multi-amplitude MSK but others [10–12]. The demand for pushing the bit rate higher than 40–100 Gb/s ethernet has driven research into modu- lation formats that would offer an effective higher bit rate using N bits/symbol so that a symbol rate falls into the processing speed of * Tel.: +49 8806311; fax: +49 8806303. E-mail addresses: le.nguyen.binh@eng.monash.edu.au, lb@tf.uni-kiel.de 0030-4018/$ - see front matter Ó 2008 Elsevier B.V. All rights reserved. doi:10.1016/j.optcom.2008.04.041 microwave digital circuitry. Multi-level modulation is thus attrac- tive, especially for MSK modulation format, the M-ary MSK. In this paper we thus present the generation and detection of multi-amplitude level minimum shift keying modulation formats. Novel structures of photonic transmitters using optical phase mod- ulators are proposed. Differential non-coherent balanced receivers are used for the detection of the phase evolution of multi-level MSK optical signals in association with direct detection of the amplitude levels. Transmission performance of 80 Gb/s 2-ampli- tude MSK is achieved and equivalent to 40 Gb/s binary MSK. This paper is thus organized as follows: Section 2 introduces the con- cept of MSK and M-ary MSK modulation formats. Section 3 then proposes the optical transmitter employing two cascaded optical phase modulators (OPM), the operation principles and necessary equations for generation of M-ary MSK optical signals. The detec- tion of multi-amplitude MSK is also described with both the detec- tion of the amplitude levels by direct detection and the detection of the evolution of the continuous phase by balanced receiver in asso- ciation with a delayed interferometer. Section 4 evaluates the transmission performance of M-ary MSK by superimposing the BER of both amplitude and phase error rates. 80 Gb/s 2-amplitude MSK is compared with 40 Gb/s binary MSK modulation formats. Section 5 makes some concluding remarks. 2. Multi-amplitude CPM (MACPM) and multi-amplitude MSK (MAMSK) One of the important digital modulation schemes is the mini- mum shift keying (MSK), which combines many attractive charac- teristics, including constant envelop, compact power spectrum,

4246 L.N. Binh / Optics Communications 281 (2008) 4245–4253 good error rate performance. In addition if multi-level amplitude is incorporated the symbol rate that would be reduced and hence more effective in long haul transmission and upgrading of one speciﬁc channel of lower bit rate multi-wavelength optical trans- port systems. This is the principal feature of the proposed modula- tion scheme that we introduce in this section. Multi-amplitude MSK (MAMSK) is a special case of MACPM (multi-amplitude continuous phase modulation) that enables mul- ti-level (PAM- or QAM-like) transmission scheme in combination with the preservation of bandwidth-efﬁcient transitional phase continuity property of consecutive transmitted symbols (CPM-like signals). The mapping scheme of data bits a and b to the continu- ous changes of amplitudes and phase of the carriers in a dual-level (2-amplitude levels) MSK is shown in Table 1. In MACPM format, N-bit logic sequences are used for generating signals which can be generally expressed as in Eq. (1) [1], thus the optical signal s(t) can be represented as sðtÞ ¼ AN cosðxct þ /Nðt; aÞÞ þ where Bm cosðxct þ /mðt; bmÞÞ X N1 m¼1 X n1 ð1Þ ð2Þ ð3Þ ak nT 6 t 6 ðn þ 1ÞT /Nðt; aÞ ¼ phanqðt nTÞ þ ph k¼1 /mðt; bmÞ ¼ pan h þ bmn þ 1 qðt nTÞ ak h þ bmk þ 1 mT 6 t 6 ðm þ 1ÞT X þ p n1 2 k¼1 2 In a generalized MACPM transmitter, the values of logic se- quences an and bmn are statistically independent and may be taken from the set of {±1, ±3, ±5,. . .}. An and Bm are the amplitude levels of the signal states, which are either in phase or p phase shift with the largest level component at the end of nth symbol interval; q(t) is the pulse shaping function and h is the frequency modulation in- dex. Eqs. (2) and (4) show the constraints of consecutive phases /m to maintaining the phase continuity characteristic of CPM sequences. In the special case of MAMSK, h = 1/2 and the phase shaping function q(tnT) is a periodic ramp signal with duty cycle of 4T. Eqs. (2) and (4) are, therefore, simpliﬁed to Eqs. (5) and (7), respectively. n1 X þ ph /Nðt; aÞ ¼ phan t nT /mðt; bmÞ ¼ pIn h þ bmn þ 1 bk h þ bmk þ 1 mT 6 t 6 ðm þ 1ÞT t nT X ak nT 6 t 6 ðn þ 1ÞT þ p k¼1 n1 2 T T ð4Þ ð5Þ k¼1 2 The optical MAMSK transmitter conﬁguration with N = 2 and the signal space trajectories in case of N = 2 and 3 following those of standard MSK schemes [1]. Thus there are two requirements for a MAMSK transmitter: ﬁrstly, it must provide the switching of the amplitude level and the phase variation of the lightwaves and secondly the synchroni- Table 1 Mapping of data information in dual-level MSK format a 1 1 1 1 b 1 1 1 1 Remarks on signal constellation Amplitude unchanged, phase continuously increased Amplitude unchanged, phase continuously decreased Amplitude changed, phase continuously increased Amplitude changed, phase continuously decreased zation of the continuity of the phase of the lightwave carrier at the transitional instant between the symbols. 3. Optical MSK and multi-amplitude MSK transmitters The optical MSK transmitters from Refs [2–4] can be integrated in the proposed generation scheme of optical MAMSK signals. 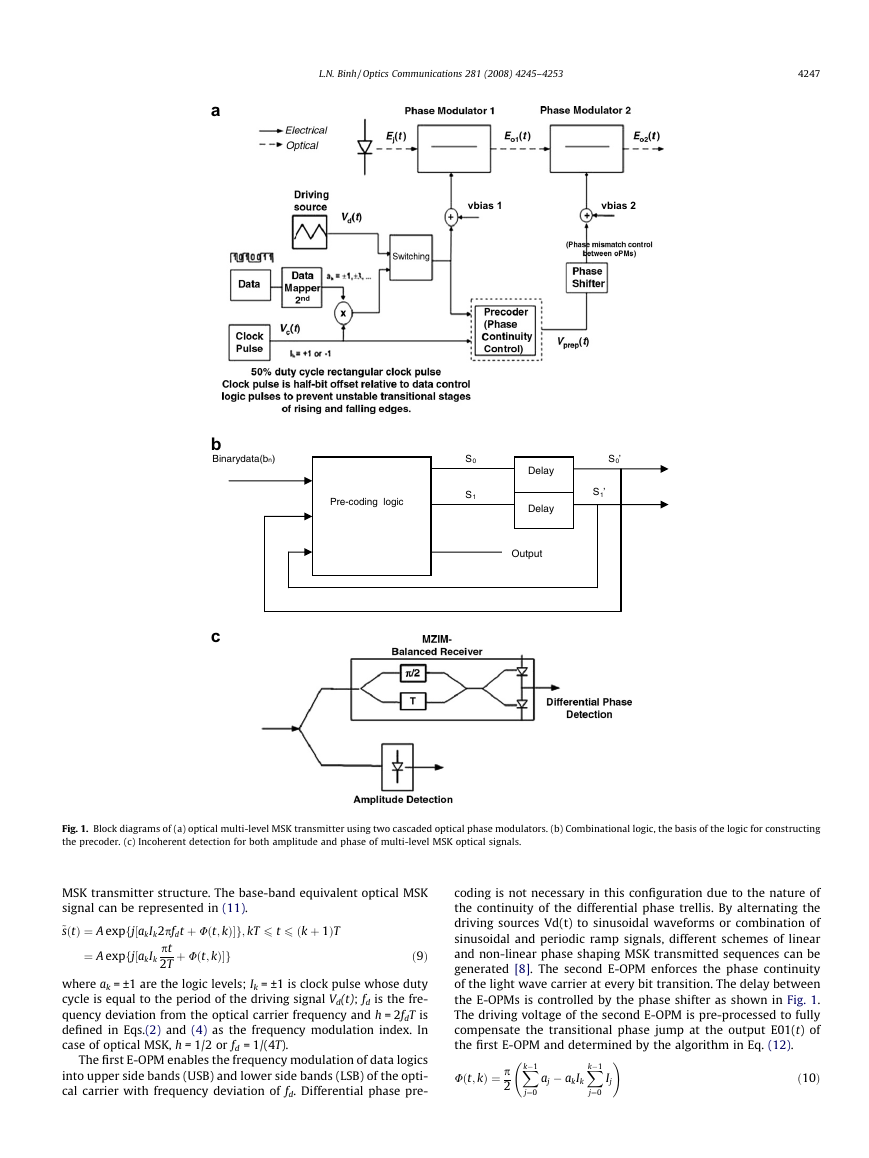However, in this paper, we propose a new simple-in-implementa- tion optical MSK transmitter conﬁguration employing two high- speed cascaded electro-optic phase modulators (E-OPMs) as shown in the block diagrams of Fig. 1a. The ﬁrst OPM plays the role of modulating the binary data logic into two carrier frequencies deviating from the optical carrier of the laser source by a quarter of the bit rate. The second OPM enforces the phase continuity of the lightwave carrier at every bit transition. The driving voltage of this second OPM is pre-coded in such a way that the phase discrepancy due to frequency modu- lation of the ﬁrst OPM is compensated, hence preserving the phase continuity characteristic of MSK signal. 1 þ bnS0 1 þ bnS0 1 þ bnS0 0S0 0S0 0S0 0S0 1 þ bnS0 The mapping table of Table 1 can be used to derive the logic table that we can then construct combinational logic diagram. For positive half cycle cosine wave and positive half cycle sine wave, the output is 1; for negative half cycle triangular wave (for linear) (or cosine wave) and negative half cycle of the triangular wave sine wave, the output is 0. Then, Karnaugh maps can then be constructed to derive the logic gates within the pre-coding logic block, based on the truth table. The following three pre-coding logic equations can be derived for binary MSK (see Fig. 1b): S0 ¼ bnS0 S1 ¼ S0 1 ¼ bnS0 Output ¼ S0 ð6Þ ð7Þ ð8Þ For higher level it is not difﬁcult to derive the logic states but much easier by using logic block set of MATLAB Simulink1 on which we have based our simulation model. These logical states S0 1 and S0 0are then conditioned to appropriate voltage level which is then fed to the switching circuit (see Fig. 1a) to control the timing of the switching the sections of the triangular wave (or sine wave gen- erator) to enforce the modulation of the phase of the carrier by driv- ing the optical phase modulator. The amplitude of the carrier is set by the mapper shown in Fig. 1a that would map the number of bits into equivalent numbers as indicated. 1 1 Utilizing this double phase modulation conﬁguration, different types of linear and non-linear CPM phase shaping signals including MSK, strongly-linear MSK and weakly nonlinear-sinusoidal MSK can be generated [9]. The optical spectra of the modulation scheme obtained conﬁrm the bandwidth efﬁciency of this novel optical MSK transmitter (shown later in Fig. 6). If the triangular wave gen- erator of Fig. 1a is replaced by a sinusoidal wave then the phase variation over the period of a symbol is not linear but nonlinear. This phase nonlinearity is not high if the amplitude of the wave is not large and in this case we term the modulation scheme as weakly nonlinear MSK. On the other hand if the amplitude is high then the phase variation is strongly departing from the linear trian- gular trend and this case is termed as strongly nonlinear MSK modulation. E-OPMs and E-O interferometers operating at high frequency using resonant-type electrodes have been studied and proposed in [5,6]. In addition, high-speed electronic driving circuits evolved with the ASIC technology using 0.1 lm GaAs P-HEMT or InP HEMTs [7] enables the feasibility in realization of the proposed optical 1 See details of MATLAB Simulink at http://www.mathworks.com/

L.N. Binh / Optics Communications 281 (2008) 4245–4253 4247 vbias 1 vbias 2 Pre-coding logic S0’ S1’ S0 S1 Delay Delay Output a b Binarydata(bn) c Fig. 1. Block diagrams of (a) optical multi-level MSK transmitter using two cascaded optical phase modulators. (b) Combinational logic, the basis of the logic for constructing the precoder. (c) Incoherent detection for both amplitude and phase of multi-level MSK optical signals. MSK transmitter structure. The base-band equivalent optical MSK signal can be represented in (11). ~sðtÞ ¼ A expfj½akIk2pfdt þ Uðt; kÞg; kT 6 t 6 ðk þ 1ÞT ¼ A expfj½akIk pt 2T þ Uðt; kÞg ð9Þ where ak = ±1 are the logic levels; Ik = ±1 is clock pulse whose duty cycle is equal to the period of the driving signal Vd(t); fd is the fre- quency deviation from the optical carrier frequency and h = 2fdT is deﬁned in Eqs.(2) and (4) as the frequency modulation index. In case of optical MSK, h = 1/2 or fd = 1/(4T). The ﬁrst E-OPM enables the frequency modulation of data logics into upper side bands (USB) and lower side bands (LSB) of the opti- cal carrier with frequency deviation of fd. Differential phase pre- coding is not necessary in this conﬁguration due to the nature of the continuity of the differential phase trellis. By alternating the driving sources Vd(t) to sinusoidal waveforms or combination of sinusoidal and periodic ramp signals, different schemes of linear and non-linear phase shaping MSK transmitted sequences can be generated [8]. The second E-OPM enforces the phase continuity of the light wave carrier at every bit transition. The delay between the E-OPMs is controlled by the phase shifter as shown in Fig. 1. The driving voltage of the second E-OPM is pre-processed to fully compensate the transitional phase jump at the output E01(t) of the ﬁrst E-OPM and determined by the algorithm in Eq. (12). ! aj akIk Ij ð10Þ X k1 j¼0 Uðt; kÞ ¼ p 2 X k1 j¼0

4248 L.N. Binh / Optics Communications 281 (2008) 4245–4253 The second E-OPM receives the data gated signals which once ap- plied to its electrode may create spikes if there are timing errors of the synchronization of electronic signals. So in order to mitigate the effects of overshooting at rising and falling edges of the elec- tronic circuits, the clock pulse Vc(t) is offset by one bit delay with the driving voltages Vd(t). 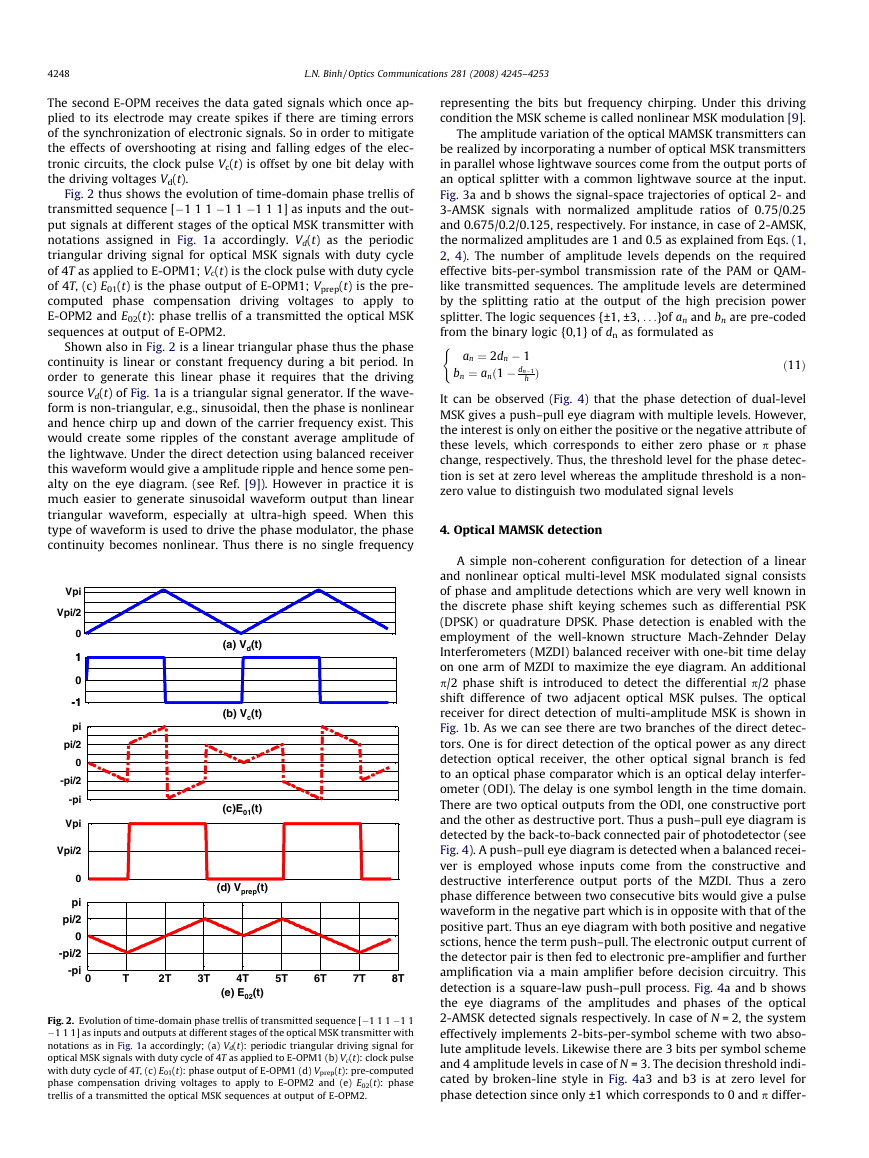Fig. 2 thus shows the evolution of time-domain phase trellis of transmitted sequence [1 1 1 1 1 1 1 1] as inputs and the out- put signals at different stages of the optical MSK transmitter with notations assigned in Fig. 1a accordingly. Vd(t) as the periodic triangular driving signal for optical MSK signals with duty cycle of 4T as applied to E-OPM1; Vc(t) is the clock pulse with duty cycle of 4T, (c) E01(t) is the phase output of E-OPM1; Vprep(t) is the pre- computed phase compensation driving voltages to apply to E-OPM2 and E02(t): phase trellis of a transmitted the optical MSK sequences at output of E-OPM2. Shown also in Fig. 2 is a linear triangular phase thus the phase continuity is linear or constant frequency during a bit period. In order to generate this linear phase it requires that the driving source Vd(t) of Fig. 1a is a triangular signal generator. If the wave- form is non-triangular, e.g., sinusoidal, then the phase is nonlinear and hence chirp up and down of the carrier frequency exist. This would create some ripples of the constant average amplitude of the lightwave. Under the direct detection using balanced receiver this waveform would give a amplitude ripple and hence some pen- alty on the eye diagram. (see Ref. [9]). However in practice it is much easier to generate sinusoidal waveform output than linear triangular waveform, especially at ultra-high speed. When this type of waveform is used to drive the phase modulator, the phase continuity becomes nonlinear. Thus there is no single frequency Vpi Vpi/2 0 1 1 0 -1 -1 pi pi/2 0 -pi/2 -pi Vpi Vpi/2 0 pi pi/2 0 -pi/2 -pi (a) Vd(t) (b) Vc(t) (c)E01(t) (d) Vprep(t) 0 T 2T 3T 4T 5T 6T 7T 8T (e) E02(t) Fig. 2. Evolution of time-domain phase trellis of transmitted sequence [1 1 1 1 1 1 1 1] as inputs and outputs at different stages of the optical MSK transmitter with notations as in Fig. 1a accordingly; (a) Vd(t): periodic triangular driving signal for optical MSK signals with duty cycle of 4T as applied to E-OPM1 (b) Vc(t): clock pulse with duty cycle of 4T, (c) E01(t): phase output of E-OPM1 (d) Vprep(t): pre-computed phase compensation driving voltages to apply to E-OPM2 and (e) E02(t): phase trellis of a transmitted the optical MSK sequences at output of E-OPM2. representing the bits but frequency chirping. Under this driving condition the MSK scheme is called nonlinear MSK modulation [9]. The amplitude variation of the optical MAMSK transmitters can be realized by incorporating a number of optical MSK transmitters in parallel whose lightwave sources come from the output ports of an optical splitter with a common lightwave source at the input. 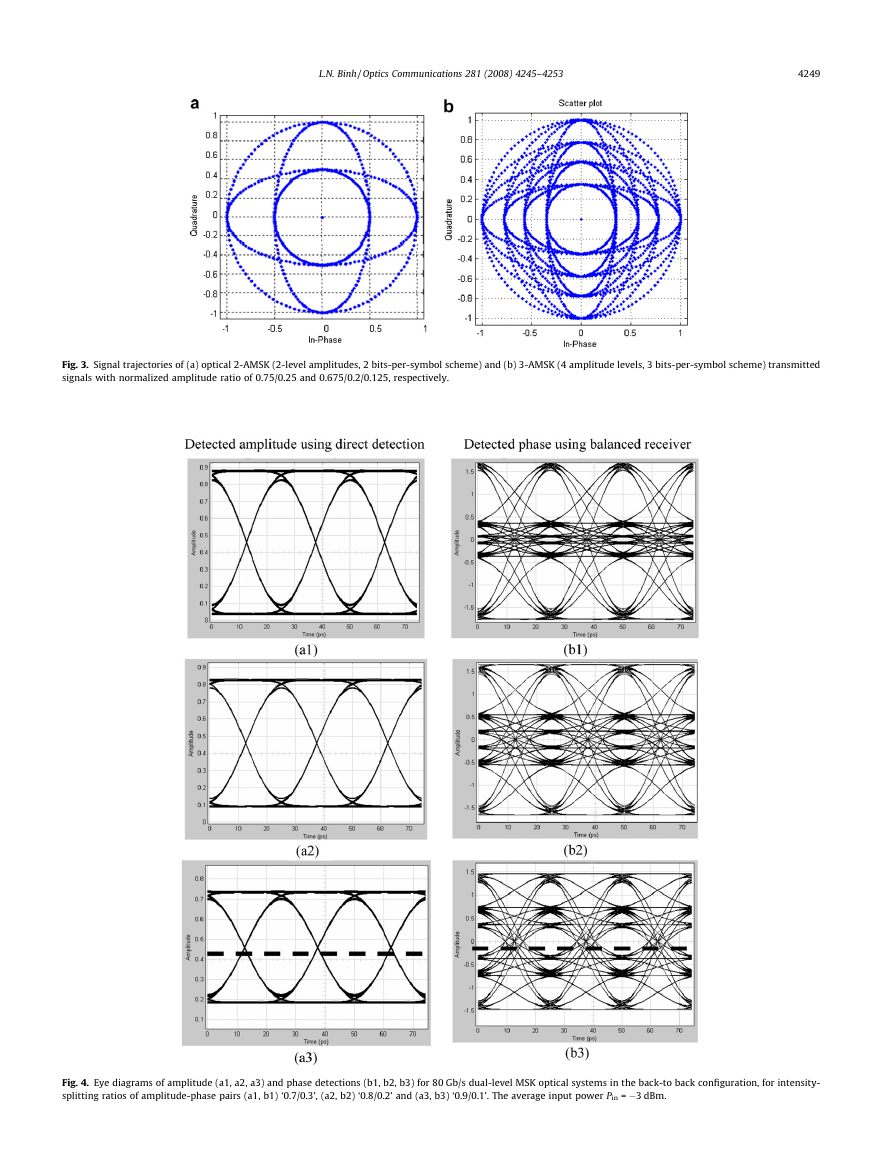Fig. 3a and b shows the signal-space trajectories of optical 2- and 3-AMSK signals with normalized amplitude ratios of 0.75/0.25 and 0.675/0.2/0.125, respectively. For instance, in case of 2-AMSK, the normalized amplitudes are 1 and 0.5 as explained from Eqs. (1, 2, 4). The number of amplitude levels depends on the required effective bits-per-symbol transmission rate of the PAM or QAM- like transmitted sequences. The amplitude levels are determined by the splitting ratio at the output of the high precision power splitter. The logic sequences {±1, ±3, . . 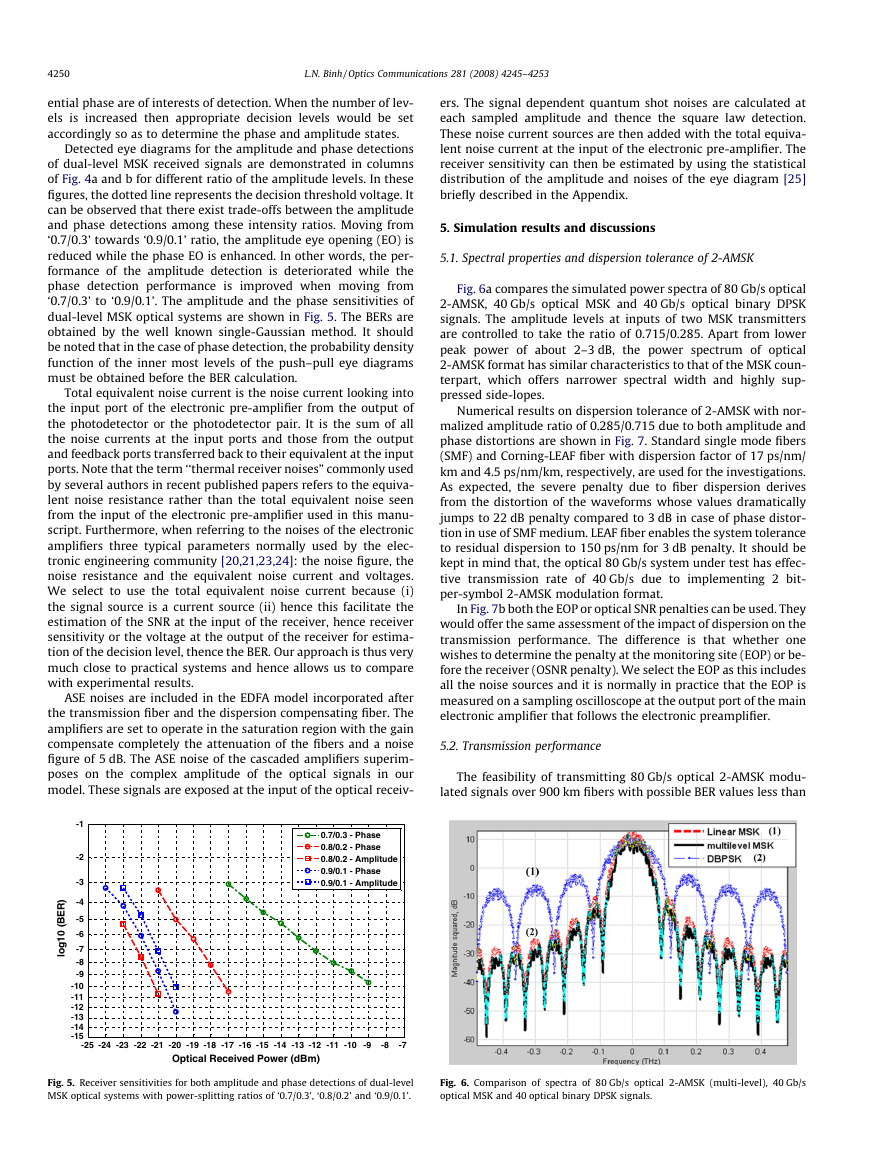.}of an and bn are pre-coded from the binary logic {0,1} of dn as formulated as ( an ¼ 2dn 1 bn ¼ anð1 dn1 h Þ ð11Þ It can be observed (Fig. 4) that the phase detection of dual-level MSK gives a push–pull eye diagram with multiple levels. However, the interest is only on either the positive or the negative attribute of these levels, which corresponds to either zero phase or p phase change, respectively. Thus, the threshold level for the phase detec- tion is set at zero level whereas the amplitude threshold is a non- zero value to distinguish two modulated signal levels 4. Optical MAMSK detection A simple non-coherent conﬁguration for detection of a linear and nonlinear optical multi-level MSK modulated signal consists of phase and amplitude detections which are very well known in the discrete phase shift keying schemes such as differential PSK (DPSK) or quadrature DPSK. Phase detection is enabled with the employment of the well-known structure Mach-Zehnder Delay Interferometers (MZDI) balanced receiver with one-bit time delay on one arm of MZDI to maximize the eye diagram. An additional p/2 phase shift is introduced to detect the differential p/2 phase shift difference of two adjacent optical MSK pulses. The optical receiver for direct detection of multi-amplitude MSK is shown in Fig. 1b. As we can see there are two branches of the direct detec- tors. One is for direct detection of the optical power as any direct detection optical receiver, the other optical signal branch is fed to an optical phase comparator which is an optical delay interfer- ometer (ODI). The delay is one symbol length in the time domain. There are two optical outputs from the ODI, one constructive port and the other as destructive port. Thus a push–pull eye diagram is detected by the back-to-back connected pair of photodetector (see Fig. 4). A push–pull eye diagram is detected when a balanced recei- ver is employed whose inputs come from the constructive and destructive interference output ports of the MZDI. Thus a zero phase difference between two consecutive bits would give a pulse waveform in the negative part which is in opposite with that of the positive part. Thus an eye diagram with both positive and negative sctions, hence the term push–pull. The electronic output current of the detector pair is then fed to electronic pre-ampliﬁer and further ampliﬁcation via a main ampliﬁer before decision circuitry. This detection is a square-law push–pull process. Fig. 4a and b shows the eye diagrams of the amplitudes and phases of the optical 2-AMSK detected signals respectively. In case of N = 2, the system effectively implements 2-bits-per-symbol scheme with two abso- lute amplitude levels. Likewise there are 3 bits per symbol scheme and 4 amplitude levels in case of N = 3. The decision threshold indi- cated by broken-line style in Fig. 4a3 and b3 is at zero level for phase detection since only ±1 which corresponds to 0 and p differ-

L.N. Binh / Optics Communications 281 (2008) 4245–4253 4249 Fig. 3. Signal trajectories of (a) optical 2-AMSK (2-level amplitudes, 2 bits-per-symbol scheme) and (b) 3-AMSK (4 amplitude levels, 3 bits-per-symbol scheme) transmitted signals with normalized amplitude ratio of 0.75/0.25 and 0.675/0.2/0.125, respectively. Fig. 4. Eye diagrams of amplitude (a1, a2, a3) and phase detections (b1, b2, b3) for 80 Gb/s dual-level MSK optical systems in the back-to back conﬁguration, for intensity- splitting ratios of amplitude-phase pairs (a1, b1) ‘0.7/0.3’, (a2, b2) ‘0.8/0.2’ and (a3, b3) ‘0.9/0.1’. The average input power Pin = 3 dBm.

4250 L.N. Binh / Optics Communications 281 (2008) 4245–4253 ential phase are of interests of detection. When the number of lev- els is increased then appropriate decision levels would be set accordingly so as to determine the phase and amplitude states. Detected eye diagrams for the amplitude and phase detections of dual-level MSK received signals are demonstrated in columns of Fig. 4a and b for different ratio of the amplitude levels. In these ﬁgures, the dotted line represents the decision threshold voltage. It can be observed that there exist trade-offs between the amplitude and phase detections among these intensity ratios. Moving from ‘0.7/0.3’ towards ‘0.9/0.1’ ratio, the amplitude eye opening (EO) is reduced while the phase EO is enhanced. In other words, the per- formance of the amplitude detection is deteriorated while the phase detection performance is improved when moving from ‘0.7/0.3’ to ‘0.9/0.1’. The amplitude and the phase sensitivities of dual-level MSK optical systems are shown in Fig. 5. The BERs are obtained by the well known single-Gaussian method. It should be noted that in the case of phase detection, the probability density function of the inner most levels of the push–pull eye diagrams must be obtained before the BER calculation. Total equivalent noise current is the noise current looking into the input port of the electronic pre-ampliﬁer from the output of the photodetector or the photodetector pair. It is the sum of all the noise currents at the input ports and those from the output and feedback ports transferred back to their equivalent at the input ports. Note that the term ‘‘thermal receiver noises” commonly used by several authors in recent published papers refers to the equiva- lent noise resistance rather than the total equivalent noise seen from the input of the electronic pre-ampliﬁer used in this manu- script. Furthermore, when referring to the noises of the electronic ampliﬁers three typical parameters normally used by the elec- tronic engineering community [20,21,23,24]: the noise ﬁgure, the noise resistance and the equivalent noise current and voltages. We select to use the total equivalent noise current because (i) the signal source is a current source (ii) hence this facilitate the estimation of the SNR at the input of the receiver, hence receiver sensitivity or the voltage at the output of the receiver for estima- tion of the decision level, thence the BER. Our approach is thus very much close to practical systems and hence allows us to compare with experimental results. ASE noises are included in the EDFA model incorporated after the transmission ﬁber and the dispersion compensating ﬁber. The ampliﬁers are set to operate in the saturation region with the gain compensate completely the attenuation of the ﬁbers and a noise ﬁgure of 5 dB. The ASE noise of the cascaded ampliﬁers superim- poses on the complex amplitude of the optical signals in our model. These signals are exposed at the input of the optical receiv- ers. The signal dependent quantum shot noises are calculated at each sampled amplitude and thence the square law detection. These noise current sources are then added with the total equiva- lent noise current at the input of the electronic pre-ampliﬁer. The receiver sensitivity can then be estimated by using the statistical distribution of the amplitude and noises of the eye diagram [25] brieﬂy described in the Appendix. 5. Simulation results and discussions 5.1. Spectral properties and dispersion tolerance of 2-AMSK Fig. 6a compares the simulated power spectra of 80 Gb/s optical 2-AMSK, 40 Gb/s optical MSK and 40 Gb/s optical binary DPSK signals. The amplitude levels at inputs of two MSK transmitters are controlled to take the ratio of 0.715/0.285. Apart from lower peak power of about 2–3 dB, the power spectrum of optical 2-AMSK format has similar characteristics to that of the MSK coun- terpart, which offers narrower spectral width and highly sup- pressed side-lopes. Numerical results on dispersion tolerance of 2-AMSK with nor- malized amplitude ratio of 0.285/0.715 due to both amplitude and phase distortions are shown in Fig. 7. Standard single mode ﬁbers (SMF) and Corning-LEAF ﬁber with dispersion factor of 17 ps/nm/ km and 4.5 ps/nm/km, respectively, are used for the investigations. As expected, the severe penalty due to ﬁber dispersion derives from the distortion of the waveforms whose values dramatically jumps to 22 dB penalty compared to 3 dB in case of phase distor- tion in use of SMF medium. LEAF ﬁber enables the system tolerance to residual dispersion to 150 ps/nm for 3 dB penalty. It should be kept in mind that, the optical 80 Gb/s system under test has effec- tive transmission rate of 40 Gb/s due to implementing 2 bit- per-symbol 2-AMSK modulation format. In Fig. 7b both the EOP or optical SNR penalties can be used. They would offer the same assessment of the impact of dispersion on the transmission performance. The difference is that whether one wishes to determine the penalty at the monitoring site (EOP) or be- fore the receiver (OSNR penalty). We select the EOP as this includes all the noise sources and it is normally in practice that the EOP is measured on a sampling oscilloscope at the output port of the main electronic ampliﬁer that follows the electronic preampliﬁer. 5.2. Transmission performance The feasibility of transmitting 80 Gb/s optical 2-AMSK modu- lated signals over 900 km ﬁbers with possible BER values less than ) R E B ( 0 1 g o l -1 -2 -3 -4 0.7/0.3 - Phase 0.8/0.2 - Phase 0.8/0.2 - Amplitude 0.9/0.1 - Phase 0.9/0.1 - Amplitude -5 -6 -7 -8 -9 -10 -11 -12 -13 -14 -15 -25 -24 -23 -22 -21 -20 -19 -18 -17 -16 -15 -14 -13 -12 -11 -10 -9 -8 -7 Optical Received Power (dBm) Fig. 5. Receiver sensitivities for both amplitude and phase detections of dual-level MSK optical systems with power-splitting ratios of ‘0.7/0.3’, ‘0.8/0.2’ and ‘0.9/0.1’. Fig. 6. Comparison of spectra of 80 Gb/s optical 2-AMSK (multi-level), 40 Gb/s optical MSK and 40 optical binary DPSK signals.

L.N. Binh / Optics Communications 281 (2008) 4245–4253 4251 ) B d ( y t l a n e P n e p O e y E i s n o i t r o t s D e s a h P d n a e d u t i l p m A f o 24 22 20 18 16 14 12 10 8 6 4 2 0 -200 EOP Amp LEAF EOP Amp SMF28 EOP Phase LEAF EOP Phase SMF -150 -100 -50 0 50 100 150 200 Residual Dispersion (ps/nm) Fig. 7. Numerical results on dispersion tolerance of 80 Gb/s optical 2-AMSK (effectively 40 Gb/s transmission rate) with normalized amplitude ratio of 0.285/ 0.715 due to both waveform and phase distortions. 1e-12 is numerically demonstrated in Fig. 8. The simulation con- sists of 80 Gbps random generator with 128-bit sequence, 10 spans of 90 km Vascade ﬁbers (60 km + 17 ps/nm/km and 30 km of 34 ps/nm/km and also fully compensated dispersion slope), opti- cal ﬁlter bandwidth of 80 GHz. The main reason for us to use Vascade ﬁbers because their dispersion and compensating proper- ties are well matched over the spectral range of interests. Naturally other types of ﬁbers such as standard SMF, Corning LEAF can be used together with dispersion compensating modules. The optical ampliﬁers (Er: doped Fiber ampliﬁer-EDFA) are incorporated with a gain of 19 dB to compensate for the loss of the transmission ﬁber and a noise ﬁgure of 5 dB. Accumulated noises of cascaded ampli- ﬁers are measured in the model and compared with experimental values which agree well with each other. The quantum shot noises which are signal dependent are also built in the model and checked with typical values in practice. These quantum shot noises are very important in multi- amplitude level modulation because the con- tribution of noises at each level would be different. Electronic noise p of the receiver is modelled with equivalent noise current density of and dark current of 2 10 nA (2 electrical ampliﬁer of 20 pA/ photodiodes for balanced receiver). Thus with the total equivalent electronic noises as seen from the input of the electronic preampli- ﬁer, our transmission model really represents a very close to exper- imental in which the polarization mode dispersion (PMD) and statistical ﬂuctuation due to environment can be controlled and suppressed. transmission laboratory environment ﬃﬃﬃﬃﬃﬃ Hz This conﬁguration yields the receiver sensitivity at BER = 1e-9 in back-to-back case to be approximately 23 dBm and 25.5 dBm for 2-AMSK and MSK optical receivers respectively. As explained above from Fig. 6, the peak power of 2-AMSK is approximately 2–3 dB lower than that of its MSK counterpart. The eye diagrams are obtained after a 9th order Bessel electrical ﬁl- ter with a bandwidth of 32 GHz. 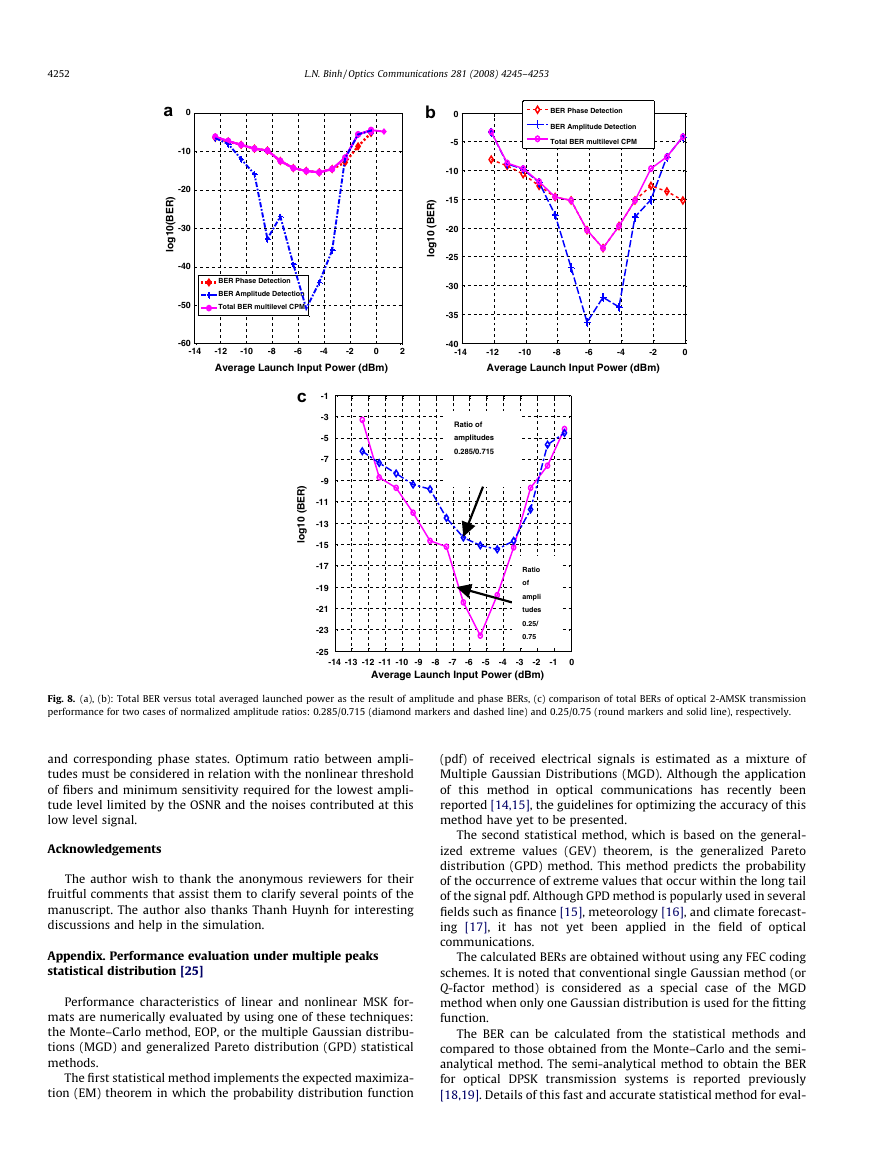Launched peak input power is var- ied from 10 to +3 dBm which corresponds to average powers ranging from 12.5 dBm to 0.5 dBm. Fig. 8a and b shows the total BER as the result of the performance of amplitude, phase detection in case of normalized amplitude levels of 0.285/0.715 and 0.25/ 0.75 ratios, respectively. In Fig. 8c, the plot of transmission perfor- mance with diamond markers and dashed line represents the case of normalized amplitude levels of 0.285/0.715 whereas round markers and solid line curve are used in the 0.25/0.75 counterpart. The optimal BERs of 1e-15 and 1e-23 are obtained at average input power of 4.5 and 5.5 dBm, respectively. These results raise the needs of optimizing the amplitude levels for the best BER of optical 2-AMSK signal transmission. In our simulation model the nonlinear effects due to self phase modulation, four wave mixing or stimulated Raman scattering are included in the nonlinear Schroedinger equation and the split step Fourier method that represents the evolution of the sampled signals through the ﬁbers. The amplitude of the lightwave signals is set by varying the average optical power at the input of the transmission ﬁber of the ﬁst span. This power can set above or be- low the nonlinear power threshold of the transmission ﬁber. The penalty on the eye diagram can then be obtained. Noises are superimposed on the signal amplitudes at each sam- pled instant. The NF of EDFAs are set at 5 dB. The OSNR is set depending on the optical power at the input of the transmission ﬁber which is set below the nonlinear threshold (3 dBm). So OSNR varies according to our study of dispersion tolerance of chromatic dispersion or nonlinear impact. If it is at the region just below the nonlinear threshold then the OSNR (0.1 nm) is about 13–19 dB. Regarding the optimum receiver sensitivity of 5 dBm of the proposed MAMSK modulation scheme, this can be compared with the experimental results reported by Gnauck et al. [26] for on–off keying and differential phase shift keying (DPSK) formats. The most appropriate format to be used for comparison is the 67% BAL DPSK which uses RZ DPSK with pulse width of 67% bit period, note that no NRZ format. Note that no NRZ format was used in [26]. With the balanced receiver the optimum value is estimated at 1 dBm for a BER of 1e-9 for 42.7 Gb/s Bal DPSK transmission over a dispersion compensated loop of 330 km incorporating (4 2+1) EDFAs plus Raman distributed ampliﬁcation. After 1980 km trans- mission the noises due to EDFAs are higher than our proposed transmission system and thus higher launched power is required. While with our sensitivity of 5 dBm, the BER is 1e-20 or lower for a ratio of the amplitude levels of 0.25/0.75. This sensitivity level is reasonable as under our simulation we expect the noises due to the switching of the data stream in and out of the circulating loop of [26] do not exist. 6. Conclusion We have proposed a modulation scheme based on multi-ampli- tude and continuous phase, the multi-amplitude minimum shift keying scheme for effective enhancement of the transmission capacity but detection at lower symbol rate. Also proposed is a new conﬁguration and simple implementation of optical MSK transmitters using two cascaded E-OPMs which reduce the com- plexity of photonic components for generation of multi-amplitude MSK optical signals. These modular optical MSK transmitter structures can then be integrated in parallel to form optical mul- ti-amplitude MSK transmitters. The number of signal amplitude levels and phase states can be easily increased by cascading or cas- cading optical binary MSK transmitters. Comparison of spectral properties compared to the MSK and DPSK counterparts and simu- lated dispersion tolerance results demonstrate the effectiveness of the modulation scheme. Numerical results of the transmission per- formance over 900 km multi-span length have been presented for two different cases of normalized amplitude ratios of the 2-AMSK modulation format. We have yet optimized the ratio of the amplitude levels. Ideally the amplitude level should be 50:50 but due to the signal-depen- dent quantum shot noises the noise contributed due to the upper amplitude level is higher than the lower level and we have achieved the best receiver sensitivity at the ratio 0.285/0.75 for dual level. Further works will be conducted for the optimization of the amplitude level ratio and phase ratio. Obviously higher number of amplitude levels can be designed without difﬁculty. However the optical receivers must be re- considered due to different contribution of noises at each level

4252 L.N. Binh / Optics Communications 281 (2008) 4245–4253 a 0 ) R E B ( 0 1 g o l -10 -20 -30 -40 -50 -60 -14 b ) R E B ( 0 1 g o l 0 -5 -10 -15 -20 -25 -30 -35 2 -40 -14 BER Phase Detection BER Amplitude Detection Total BER multilevel CPM -10 -12 -2 Average Launch Input Power (dBm) -8 -6 -4 0 BER Phase Detection BER Amplitude Detection Total BER multilevel CPM -10 -12 Average Launch Input Power (dBm) -8 -6 -4 -2 0 c ) R E B ( 0 1 g o l -1 -3 -5 -7 -9 -11 -13 -15 -17 -19 -21 -23 Ratio of amplitudes 0.285/0.715 Ratio of ampli tudes 0.25/ 0.75 -25 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 Average Launch Input Power (dBm) Fig. 8. (a), (b): Total BER versus total averaged launched power as the result of amplitude and phase BERs, (c) comparison of total BERs of optical 2-AMSK transmission performance for two cases of normalized amplitude ratios: 0.285/0.715 (diamond markers and dashed line) and 0.25/0.75 (round markers and solid line), respectively. and corresponding phase states. Optimum ratio between ampli- tudes must be considered in relation with the nonlinear threshold of ﬁbers and minimum sensitivity required for the lowest ampli- tude level limited by the OSNR and the noises contributed at this low level signal. Acknowledgements The author wish to thank the anonymous reviewers for their fruitful comments that assist them to clarify several points of the manuscript. The author also thanks Thanh Huynh for interesting discussions and help in the simulation. Appendix. Performance evaluation under multiple peaks statistical distribution [25] Performance characteristics of linear and nonlinear MSK for- mats are numerically evaluated by using one of these techniques: the Monte–Carlo method, EOP, or the multiple Gaussian distribu- tions (MGD) and generalized Pareto distribution (GPD) statistical methods. The ﬁrst statistical method implements the expected maximiza- tion (EM) theorem in which the probability distribution function (pdf) of received electrical signals is estimated as a mixture of Multiple Gaussian Distributions (MGD). Although the application of this method in optical communications has recently been reported [14,15], the guidelines for optimizing the accuracy of this method have yet to be presented. The second statistical method, which is based on the general- ized extreme values (GEV) theorem, is the generalized Pareto distribution (GPD) method. This method predicts the probability of the occurrence of extreme values that occur within the long tail of the signal pdf. Although GPD method is popularly used in several ﬁelds such as ﬁnance [15], meteorology [16], and climate forecast- ing [17], it has not yet been applied in the ﬁeld of optical communications. The calculated BERs are obtained without using any FEC coding schemes. It is noted that conventional single Gaussian method (or Q-factor method) is considered as a special case of the MGD method when only one Gaussian distribution is used for the ﬁtting function. The BER can be calculated from the statistical methods and compared to those obtained from the Monte–Carlo and the semi- analytical method. The semi-analytical method to obtain the BER for optical DPSK transmission systems is reported previously [18,19]. Details of this fast and accurate statistical method for eval-

分享到：

赞收藏

资料库

多振幅MSK的调制的实现.pdf

相关推荐

课程资源

热门标签

最新资料