logo资料库

Average irregularity representation of a rough surface for ray r....pdf

发布时间：2022-06-01 发布人：admin 分类：说明书 资料大小：0.77M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    JOURNAL OF THE OPTICAL SOCIETY OF AMERICA VOLUME 65, NUMBER 5 MAY 1975 Average irregularity representation of a rough surface for ray reflection T. S. Trowbridge Naval Missile Center, Point Mugu, California 93042 K. P. Reitz Chapman College, Orange, California 92666 (Received 6 June 1974) A new ray model is presented for the reflection of electromagnetic radiation from the rough air-material interface of a randomly rough surface. Unlike previous derivations that modeled the rough interface as consisting of microareas randomly oriented but flat (facets), this derivation models it as consisting of microareas not only randomly oriented but also randomly curved. Physically, the models are the same, but this new derivation leads to some new results. (1) For any given rough surface, there exists a single, optically smooth, curved surface of revolution of very restricted shape that will reflect radiation in the same distribution as that reflected by the rough interface. (2) Modeling that surface as an ellipsoid of revolution gives a surface-structure function that appears more accurate and useful than existing ones. (3) Unlike the facet derivations, this derivation lends itself to a normalization that gives the absolute, instead of just function. a comparative, reflectance-distribution Index Headings: Geometrical optics; Reflection; Scattering. A theory for single reflection by the rough, air-materi- al interface of a randomly rough surface was first pre- sented by Bouguer. 1 He modeled the interface as con- sisting of randomly oriented, optically flat facets, each of which behaves like a small plane mirror, that reflects a portion of the light incident on it in the manner deter- mined by Fresnel's equations for specular reflection at a flat dielectric interface. The Bouguer facet theory has been found2 6 to explain much of the reflection from rough surfaces and has undergone considerable development. The derivation of the basic theory has been refined2 ,' "-" and several models3 '4 '7 '"0'1 2'13 have been tried for the microarea dis- tribution function. This is the function that gives the relative number of facets oriented in any given direc- tion, or, more precisely, the relative total facet sur- face area per unit solid angle of surface normals pointed in any given direction. This function governs the direc- tional distribution of the scattered light. If the function is uniform with respect to the direction of the facet nor- mals, a diffuse-like distribution occurs. If most of the facets lie near the plane of the surface, a nearly specu- lar distribution occurs. interface. This paper presents a new model for ray-theory re- flection from the rough, air-material In- stead of randomly oriented flat microareas (facets), here the surface structure is modeled as an ensemble of randomly oriented and randomly curved microareas. Because for practical purposes, any curved area can be broken down into infinitesimal facets, are identical, physically. However, this new derivation leads to some new results. realistic) rough interface, there exists a single, optical- ly smooth, curved surface of revolution (termed an average surface irregularity) the same distribution as that reflected by the rough in- terface. Furthermore, the shape of the average irregu- larity can be very greatly restricted and still be general enough to represent any possible (but realistic) rough that reflects radiation into (i) For any possible (but the two models (ii) This restricted shape is similar to an interface. ellipsoid of revolution. An ellipsoid-of-revolution mod- el for the average irregularity gives a surface-structure function that appears more accurate and useful than ex- isting ones. this der- ivation lends itself to a normalization that gives the ab- solute, instead of just a comparative, reflectance-dis- tribution function. (iii) Unlike the facet derivations, For simplicity and conciseness, we derive a reflec- tance-distribution function termed' 4 the BRIDF, fri (the bidirectional reflected-intensity-distribution function). It is defined as the intensity reflected into any specified direction from an illuminated point per unit of flux in the incident beam. The more common and more gen- erally useful quantity is termed' 5 the BRDF, fr (the bi- directional reflectance-distribution function). It is de- fined as the radiance reflected into a given direction per unit of irradiance incident on the surface from another given direction. The BRDF is equal to the BRIDF di- vided by the cosine of the zenith (or sine of the eleva- tion) angle of reflection. The paper is organized as follows. First we derive then an the reflection from a single, curved microarea, ensemble of curved microareas gives a reflectance-dis- tribution function and gives it in terms of a surface structure function. The concept of the average irregu- larity is presented and validated. Next, a normaliza- tion procedure makes the reflectance-distribution func- tion an absolute quantity. An ellipsoid of revolution is used as a one-parameter model for the average irregu- larity. Last, we test the accuracy and usefulness of the resulting surface-structure function for the ellipsoid. 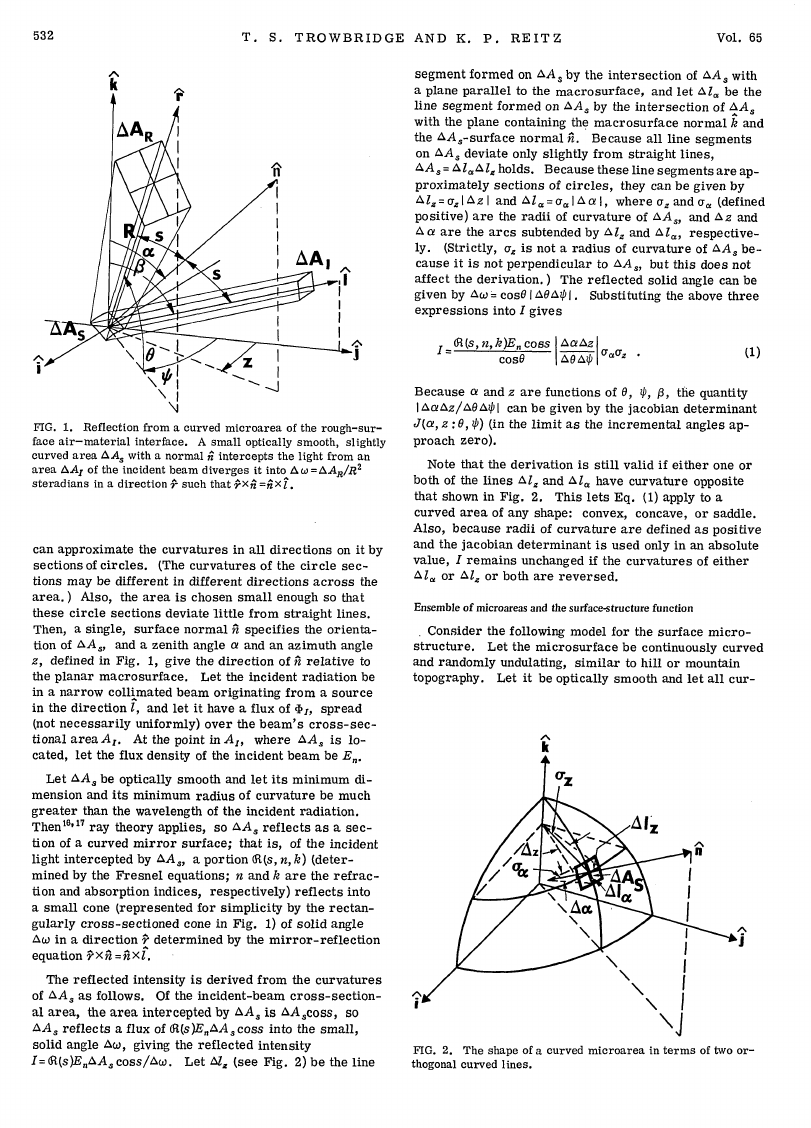INTERFACE REFLECTION MODEL Reflection from a single microarea Consider, as shown in Fig. 1, a very small, curved area AA, on an irregularity of the rough-surface micro- structure. This area is chosen small enough so that we 531
    532 T. S. TROWBRIDGE AND K. P. REITZ Vol. 65 segment formed on AAs by the intersection of AA, with a plane parallel to the macrosurface, and let Ala be the line segment formed on AA, by the intersection of AA, with the plane containing the macrosurface normal k and the AA,-surface normal il. Because all line segments on AA, deviate only slightly from straight lines, AA, = A1 1,holds. Because these line segments are ap- proximately sections of circles, A lz = a z I Az I and Ale, = a, I A ao , where az and u.e (defined positive) are the radii of curvature of AA,, and Az and A a are the arcs subtended by Al, and Ale, respective- (Strictly, a2 is not a radius of curvature of AA, be- ly. cause it is not perpendicular to AA,, but this does not affect the derivation. ) The reflected solid angle can be given by Aw = cosG I AOAOi I. Substituting three expressions into I gives they can be given by the above I =(s,n,k)EncosS cosO A|= a a.UZz I AOAO~ IeU (1) Because a and z are functions of 0, 4, (3, the quantity I AaAz/AOA0I can be given by the jacobian determinant J(a, z: 0, b) (in the limit as the incremental angles ap- proach zero). Note that the derivation is still valid if either one or both of the lines Al,2 and Ale have curvature opposite that shown in Fig. 2. This lets Eq. (1) apply to a curved area of any shape: convex, concave, or saddle. Also, because radii of curvature are defined as positive and the jacobian determinant is used only in an absolute value, I remains unchanged if the curvatures of either Ale or Al, or both are reversed. Ensemble of microareas and the surface-structure function Consider the following model for the surface micro- structure. Let the microsurface be continuously curved and randomly undulating, similar to hill or mountain topography. Let it be optically smooth and let all cur- k LIz an I I \ \ I \j iI FIG. 2. The shape of a curved microarea in terms of two or- thogonal curved lines. FIG. 1. Reflection from a curved microarea of the rough-sur- face air-material curved area AA, with a normal n intercepts the light from an area AAZ of the incident beam diverges it into A w =AAR/R2 steradians interface. A small optically smooth, slightly r such that PX4 =lX41 in a direction (The curvatures of the circle sec- can approximate the curvatures in all directions on it by sections of circles. tions may be different in different directions across the area.) Also, the area is chosen small enough so that these circle sections deviate little from straight lines. Then, a single, surface normal -A specifies the orienta- tion of AA,, and a zenith angle a and an azimuth angle z, defined in Fig. 1, give the direction of A relative to the planar macrosurface. Let the incident radiation be in a narrow collimated beam originating from a source in the direction 1, and let it have a flux of Ad, spread (not necessarily uniformly) over the beam's cross-sec- tional areaAz. At the point inA,, where AA, is lo- cated, let the flux density of the incident beam be En. Let AA, be optically smooth and let its minimum di- mension and its minimum radius of curvature be much greater than the wavelength of the incident radiation. Then"6 ' 17 ray theory applies, so AA. reflects as a sec- tion of a curved mirror surface; that is, of the incident light intercepted by AA2, a portion A (s, n, k) (deter- mined by the Fresnel equations; n and k are the refrac- tion and absorption indices, respectively) reflects into a small cone (represented for simplicity by the rectan- gularly cross-sectioned cone in Fig. 1) of solid angle Aw in a direction r determined by the mirror-reflection equation rXPi=PiXl. The reflected intensity is derived from the curvatures of AA, as follows. Of the incident-beam cross-section- al area, the area intercepted by AA, is AAcoss, so AA, reflects a flux of 6R(s)En^AAcoss into the small, solid angle Aw, giving the reflected intensity I= (R(s)EnAA. coss/Aw. Let Al2 (see Fig. 2) be the line
    May 1975 REPRESENTATION OF SURFACE 533 (3) vature radii and irregularity sizes be much larger than the wavelength of the incident radiation. Let the AA, be any small area on this undulating surface. Under these conditions, Eq. (1) gives the reflection from each small area. Equation (1) may be applied to a discon- if we disregard diffraction ef- tinuous microstructure fects at corners and edges. This allows application of Eq. (1) to a randomly scratched surface, such as ground glass or roughened metal, and to globule-pile-like structure, such as some diffusely reflecting spray- painted surfaces. Also, Eq. (1) may be applied to a surface that contains flat facets if we make their curva- ture radii not quite infinite. A very wide variety of microstructures is thus included. Finally, let the sta- tistical properties be uniform with position on the sur- face and independent of direction along the surface (no wood-like grain, or scratches with a preferred direc- tion). For given directions of illumination and observation, if his visual resolution were sharp enough an observer, to resolve the surface microstructure, would see the reflected light originating only from various points scat- tered around the microstructure. normals at these reflecting points must all be parallel, so the reflection Ii from each point is given by Eq. (1) with the same values of 0, P, a, z, and s. If for a par- ticular combination of incidence and reflection direc- tions, we let a given incident beam illuminate Nreflecting points, the total intensity reflected in the specified di- rection is given by the ensemble The microsurface N f=1 N i. IT -a I, - a,1f(s, n, k)Enj COSS | cv, z\ | coso This equation is simplified by replacing the flux density Eni in the incident beam at each reflecting point by an average value given by E.= d1/A1 , where (I is the flux of the entire incident beam and AI is the cross-sectional area of the incident beam, i 61(snk)4)j-coss I'= (2) /0,4 e _10 ) I T, 1 N Euaiuzi i. 1 cose - I func- If all dependence on the surface material and labora- tory geometry can be separated into one factor and all dependence on the surface structure into a second factor, this second factor would be a surface-structure tion. Note that all dependence on the surface structure is localized in the summation factor of Eq. (2); howev- er, this factor contains a dependence on the laboratory geometry; namely, N varies with incidence angle P. This can be removed as follows: For normal incidence and'a chosen direction of reflection, consider the set of N. reflecting points. As the incidence angle increases, this same set of points reflects into a new direction. However, the illuminated macrosurface area increases, as 1/cosf3, and some points in the additional area also contribute to the reflection. So the summation factor for the new intensity must contain some additionalu0 , juq quantities. Under the assumption that the surface is statistically uniform, these extra quantities will be sta- tistically the same as the original set, and the summa- tion factor is merely increased by 1/cost3 . Thus Eq. (2) becomes cos, n, k)3, coss I a, pJI 1 E 1J-o IT=_ a liuzi I and the incidence-angle dependence has been separated from the summation factor. However, the summation factor still retains a dependence on the laboratory ge- ometry; namely, Nn is proportional to the cross-sec- tional area Al of the incident beam. This is easily com- pensated by including the 1/AI factor with the summa- tion factor. Thus, the quantity D(a)=+1 E crjag (dimensionless) (4) is a surface-structure function, since it contains all the dependence on the surface structure and no dependence In general, this quantity is a function on anything else. of both the coordinates, a and z, of the microarea nor- mal, but we are considering only surfaces whose sta- tistical properties are directionally uniform. In the Bouguer facet theory and its refinements, the surface- structure dependence is incorporated as a microarea- distribution function, which is the relative amount of microarea oriented in a given direction or the probabili- ty density of a facet normal to be in a given direction. Like D, this function contains all the dependence on the surface structure and no dependence on anything else. Since also the two reflectance theories are identical physically, D and microarea distribution function must be related by a function of only a. Equation (3) can be put in terms of a reflectance-dis- tribution function by dividing by the incident flux PI. This gives the BRIDF. 14 Incorporating Eq. (4) in addi- tion gives f,,r (9; 0, 0) = A (s, n, k) Coss Coss cose I. J(O'z 0, 0 )ID(a) . (5) (Division by sinO gives the BRDF. 15) Average surface irregularity It might prove useful if there could exist a single op- tically smooth curved surface that would reflect light in the same distribution as that reflected by the ensemble of all the curved microareas comprising the rough sur- face. This would mean that a randomly irregular sur- face could be treated as if it consisted of a large number of small identical average irregularities or that a ran- domly irregular surface could be treated as if it were a single large curved surface (f or a "uniform f lux density" incident beam of the same total flux). Such an average ir- regularity would have to be a surface of revolution about the macrosurface normal because of the assumed direc- tional independence of the rough-surface statistics. Mathematically, the question of the possible existence of such an average irregularity may be stated as fol- lows. Let p, (a) and pe(a) be the radii of curvature for the average irregularity (defined as were, respectively, au, and ao, for a curved mircoarea), and let C be a con- stant. Does there exist a surface of revolution whose D (a) given by
    T. S. TROWBRIDGE AND K. P. REITZ Vol. 65 h (x) n PZ' (Xa - f / - x FIG. 3. Cross section of an average surface irregularity. The shape of h(x) may be restricted to the general shape illustrated and still be general enough to represent any microstructure. This general shape consists of the slope being 0 at x = 0 and in- finity at h = 0 and the curve between having no inflection points or straight-line sections. D (a) = Cp. (a)pz(a) (6) is the same as the D(a) resulting from Eq. (4)? It may be, but is not obvious, that for any realistic functional form of D (a), given by Eq. (4), there exists a surface of revolution which, by Eq. (6), can give this same functionalform of D (a). The following proves that this is indeed true and, furthermore, that the shape of the surface of revolution can be very greatly restricted and still be general enough to give any physically realistic function form of D(a). Real surfaces allow the following restrictions onD((a): (1) D(a) must exist for all values of a at least be- tween 0 and 7T/2. Any realistic rough surface will have some microareas at any given value of a between 0 and 7r/2. (2) D (a) must be finite for all values of a, since no real surface would contain any perfectly flat or perfectly cylindrical microarea. (3) D(a) is positive for all values of a. This follows from Eq. (4), since uje and 0 ,ji were defined positive. (4) D(a) must be single valued. No physical quantity can have more than one value for itself at the same point. (5) D(a) is continuous. Physical quantities never have perfect discontinuities. D [tanl 1(- h')]=C Ix| I[1+ (11')f]31 2/|1 1 I (7) We can show by elementary means that a solution h(x) must exist for this differential equation for any function- al form of D(U) [under the realistic constraints that D(a) exist and be continuous between a = 0 and #r/2]. Thus there must exist a surface of revolution hkx) capable of representing any realistic rough surface D (a). Some limits to the form of h(x) can be established such that h(x) is still capable of giving any possible realistic form of D(a); that is, because of the nature of Eq. (7), certain options are allowed, the implementation of which will not limit the ability of h(x) to give any D (a). Two options are the arbitrary choices of two boundary conditions for a second-order differential equation: one condition on h'(x) and one on h(x). This is allowed be- cause a solution to a differential equation is still a solu- tion when restricted by a boundary condition, and the set of solutions h(x) for all forms of D (a) are still solu- tions for their respective forms of D(a) even though the same boundary condition is applied to every h(x). A third option is the choice of a plus or minus sign for h (x). This is allowed because only its absolute value appears in Eq. (7). This forces Thus far, we have found two types of ways of limiting the functional form of h(x) while not limiting its ability to give any physically realistic form of D (a). These consisted of three arbitrary restrictions on h(x) that re- sult from the nature of Eq. (7) and five restrictions on D(a) that result from real surfaces. We will apply these to determine a very limited type of curve for h(x), a type that is still versatile enough to give any physically realistic form of D(a). First, let the boundary condi- tion on h'(x) be h'(O)= O. This makes the slope of h(x) zero at x= 0. Second, use the option on the sign of h"(x) to make h"(O) negative. the slope of h(x) to begin to decrease as x begins to increase (from zero). Third, the h(x) cannot have inflection points. If it did, the same value of a would occur at different parts of the curve. Because D could have different values at these two points, there could be two values of D for the one value of a. Thus, D wouldbe multiple valued, and re- striction (4) would be violated. Fourth, h(x) cannot be a straight line at any point. If it were, P,, would be in- finite at that point, by Eq. (6) D would be infinite, and restriction (2) would be violated. The slope has been forced to be level (zero) at x = 0 and to start to slope down (decrease) as x starts to increase. Because h(x) can have no inflection points or straight-line segments, the slope must continue-to decrease with increasing x. Thus the slope must become vertical (- o) at a finite value of x (say, x0). If the slope only approached verti- cal as x approached infinity, h(x) would approach a straight line, D would approach infinity, and restriction (2) would be violated. Last, let the boundary condition on h(x) be h(x0 ) = 0. This forces part of h(x) to lie on the x axis. the vertically sloping Let h (x) be a curve that when revolved about x = 0 gives the surface of revolution (see Fig. 3). The relations P =Ixi, P, =[1+ (h')a]3/2/ih"1 (primes indicate deriva- tives with respect tox), and a =tan'(- h') hold. Substi- tution into Eq. (6) gives In summary, a limited functional form of h(x) capable of giving any physically realistic functional form of D(a) resembles the curve in Fig. 3. This curve is level at x = 0, decreases with increasing x without inflection points or straight sections, and becomes vertical as it
    May 1975 REPRESENTATION OF SURFACE 535 the x axis. Or, in terms of a, the curve is crosses such that a = 0 at x= 0 and a increases without stopping or turning back with increasing x to become a = 90° at h =0. It is instructive to visualize the random topography of a rough surface as equivalent to one large surface of revolution of very restricted shape, but what substantive contribution does this make? It does not put any limits on the functional form of the surface-structure function D(a), as we have just proved. But it may give insight into the discovery of better models to represent the surface structure. the most obvious choice for a surface of revolution, an ellipsoid of revolution, gives a surface-structure that appears better than the existing ones. Perhaps other shapes for the surface of revolution will give even better results. Also, maybe ones involving two or more parameters will give very good higher-order approxima- tions. To derive the D (a) for any surface of revolution, we can follow the procedure used later for the ellipsoid. Indeed, as is shown later, function Normalization The unmeasurable variables a, z, and s and the jac- obian J terms of the measurable variables A, 0, and * are tanz = sinP cos0/(sin3+ cosz cosb) tana = sin* cos0/[sinz (sinG + cost)J coss'= cosz sina sings+ cosa cost , , , and e, z \ cose S 0utt) 4coss sin d ( 5g (8 (9 (10 )) (11 L) this by 4P gives the BRIDF for the spherical mirror, frx(0;90 0 , 0) = (RO)p2 Z()/[4'np(QT/2)] (13) For the rough-surface model at normal incidence and reflection,: = 0, 0 = 7r/2, a = 0, s = 0, and P2 (O)= 0 oc- cur, and Eq. (12) becomes frA(090" , 0)= 4C(R(0)Pa (0)lim[p(a)/sina] ao- . (14) Equating Eqs. (13) and (14), solving for the normaliza- tion constant C, and substituting C into Eq. (12), we obtain the normalized or absolute BRIDF, f ,1 fr G O=61(s4rcos- p2(7r/2)lim[P(a)/sina]sinca Pa(o)pa a)pg(a) - Ellipsoid of revolution average-surface-irregularity approximation a- 0 (15) A sphere is one possible model for the average sur- face irregularity, but it contains no parameter that can be varied An ellipsoid of revolution to change the surface structure. h=e(1 - x2)1/ 2 (16) has one such parameter e, the ratio of the length of the axis rotated about to the length of the axis rotated. As e decreases, the model irregularity becomes flatter and reflects more light in the specular direction. This is a useful property, because the wide variety of real sur- faces contains a continuous distribution of diffuse to highly specular surfaces. Evaluating Eq. (15) for the h(x) of Eq. (16) -h'=tana, r1 ,.X - x=tanu(tan~a+e2) 1/2=p.(a), ,^ tw2i3/32 X l Substituting Eqs. (1 1) and (6) into (5) gives we obtain f71(f3; 0 (2 (12) As follows, the constant C can be found so as to make S)1Cpa(a)pg(a) 1 s3 z61(S) siAS ) is a surface of revolution, the region around the expression for the reflected intensity-distribution functionfri an absolute quantity. Because the average irregularity a = 0 is approximately a spherical mirror surface, of radius Pa(O). For normal incidence and reflection, the BRIDF for this spherical mirror is equal to the BRIDF of our model, f rr(0;90',0), and C is found from this equality. The focal length; of a spherical mirror is equal to half of the radius, iP (0), and collimated incident light re- flects from it into a cone with the focal point as its ver- tex. A flux of (db1/A1)AA is incident on a small area AA on the top of the mirror. If the single large sur- face of revolution is to replace all of the illuminated areas of the real surface, it must have a uniform flux density incident on all parts of it and have no radiation missing it. Therefore, the area of its base 7rp,(7r/2) must equal the incident beam cross-sectionalarea A,; therefore ,b1AA/[7rp2(7Tr/2)] is the flux incident on AA. Upon re- flection, this flux is attenuated by A(0) and is diverged into AA/[6p<,,(0)]2 steradians. Then 61(0) multiplied by the incident flux and divided by this number of stera- dians gives the reflected intensity. Additionally dividing fr a ~it f'J;00) ,fk) = 47ncosj e2 (eacosaa+sin2a)a (17) (Division by sinG gives the BRDF.) EXPERIMENTAL Earlier, we speculated that the concept of an average surface of revolution representing the surface structure might give insight into the choice of a more accurate and useful surface-structure function. The first choice, the ellipsoid of revolution, resulted function given by the last term in the surface-structure in Eq. (17). Normalized to one at a =0, it is e4 /(e2 cosS2a+ sin2 a)2 (18) The microarea distribution function for the ellipsoid is easily shown to be proportional to 'Pap,/sina and thus, by comparison with Eqs. (12) and (17), proportional to Eq. (18). 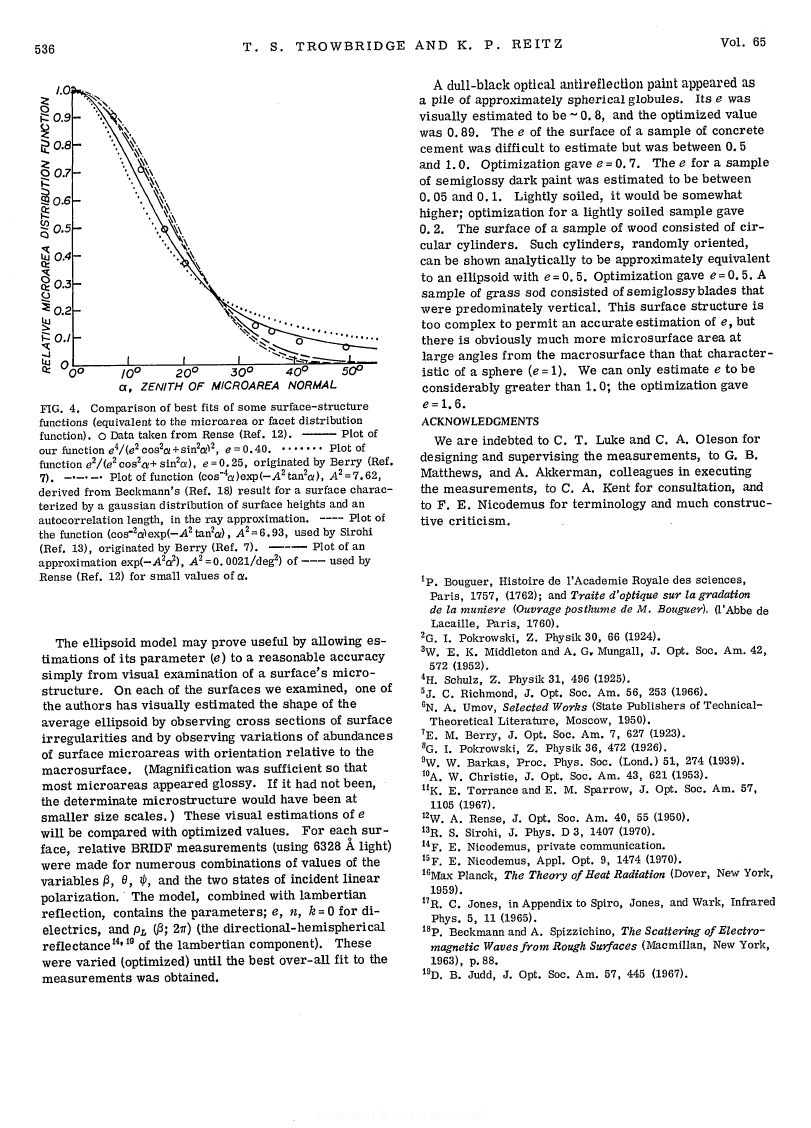Rensen2 found a way to determine the micro- area distribution function from reflectance-distribution- function measurements. Figure 4 presents these data (for light) for one rough surface, along with plots of best fits for our structure function and four microarea distri- bution functions derived by applying Rense's method to four ray-reflectance-distribution functions found in the literature.
    T. S. TROWBRIDGE AND K. P. REITZ Vol. 65 1.0. 0.9 0.8- 0.7- 0 I.- 0.6-.~ 0Z0 0.5- Lzj -J15 LaQ 0.3- 0.4- 0.2-'O./ -000I I : /00 a, ZENITH OF MICROAREA NORMAL 200 300 400 500 Plot of FIG. 4. Comparison of best fits of some surface-structure functions (equivalent to the microarea or facet distribution function). o Data taken from Rense (Ref. 12). our function e4 /(e2 cos 2 U+sin2 o) 2 , e = 0.40........ function e2 /(e2 cos 2,a+ sin2U), e=0.2 5 , originated by Berry (Ref. Plot of function (cos-4a)exp(-A 2tan2a), A2=7.62, 7). ----- derived from Beckmann's (Ref. 18) result for a surface charac- terized by a gaussian distribution of surface heights and an autocorrelation length, in the ray approximation. the function (cos-2o)exp(-A 2 tan2 a), A2= 6. 93, used by Sirohi Plot of an (Ref. 13), originated by Berry (Ref. 7). used by approximation Rense (Ref. 12) for small values of a. exp(-A 2 d), A2 = 0. 0021/deg 2 ) of --- ---- Plot of Plot of --- On each of the surfaces we examined, one of The ellipsoid model may prove useful by allowing es- timations of its parameter (e) to a reasonable accuracy simply from visual examination of a surface's micro- structure. the authors has visually estimated the shape of the average ellipsoid by observing cross sections of surface irregularities and by observing variations of abundances of surface microareas with orientation relative to the (Magnification was sufficient so that macrosurf ace. most microareas appeared glossy. the determinate microstructure would have been at smaller size scales.) These visual estimations of e will be compared with optimized values. For each sur- face, relative BRIDF measurements (using 6328 A light) were made for numerous combinations of values of the variables A, 0, 4), and the two states of incident linear polarization. The model, combined with lambertian reflection, contains the parameters; e, n, k= 0 for di- electrics, reflectance 14,19 of the lambertian were varied (optimized) until the best over-all fit to the measurements was obtained. and PL (X; 27r) (the directional-hemispherical If it had not been, component). These it would be somewhat A dull-black optical antireflectlon paint appeared as Its e was a pile of approximately spherical globules. to be - 0. 8, and the optimized value visually estimated was 0. 89. The e of the surface of a sample of concrete cement was difficult to estimate but was between 0. 5 and 1. 0. Optimization gave e = 0. 7. The e for a sample of semiglossy dark paint was estimated to be between 0. 05 and 0. 1. Lightly soiled, higher; optimization for a lightly soiled sample gave 0. 2. The surface of a sample of wood consisted of cir- cular cylinders. Such cylinders, randomly oriented, can be shown analytically to be approximately equivalent to an ellipsoid with e = O. 5. Optimization gave e= O. 5. A sample of grass sod consisted of semiglossyblades that were predominately vertical. This surface structure is too complex to permit an accurate estimation of e, but there is obviously much more microsurface area at large angles from the macrosurface than that character- (e= 1). We can only estimate e to be istic of a sphere considerably greater than 1. 0; the optimization gave e = 1. 6. ACKNOWLEDGMENTS We are indebted to C. T. Luke and C. A. Oleson for to G. B. designing and supervising the measurements, Matthews, and A. Akkerman, colleagues in executing and the measurements, to F. E. Nicodemus for terminology and much construc- tive criticism. to C. A. Kent for consultation, 'P. Bouguer, Histoire de l'Academie Royale des sciences, Paris, 1757, (1762); and Traite d'optique sur la gradation de la muniere (Ouvrage posthume de M. Bouguer). (a'Abbe de Lacaille, Paris, 1760). 2G. I. Pokrowski, Z. Physik 30, 66 (1924). 3W. E. K. Middleton and A. G. Mungall, J. Opt. Soc. Am. 42, 572 (1952). 4 H. Schulz, Z. Physik 31, 496 (1925). 5 J. C. Richmond, 6N. A. Umov, Selected Works (State Publishers of Technical- J. Opt. Soc. Am. 56, 253 (1966). Theoretical Literature, Moscow, 1950). J. Opt. Soc. Am. 7, 627 (1923). 7 E. M. Berry, 8G. I. Pokrowski, Z. Physik 36, 472 (1926). 9W. W. Barkas, Proc. Phys. Soc. (Lond.) 51, 274 (1939). 10A. W. Christie, "1K. E. Torrance and E. M. Sparrow, J. Opt. Soc. Am. 57, 1105 (1967). J. Opt. Soc. Am. 43, 621 (1953). J. Phys. D 3, 1407 (1970). i2W. A. Rense, J. Opt. Soc. Am. 40, 55 (1950). 13R. S. Sirohi, 14F. E. Nicodemus, private communication. 15 F. E. Nicodemus, Appl. Opt. 9, 1474 (1970). "Max Planck, The Theory of Heat Radiation (Dover, New York, 1959). 1 7R. C. Jones, in Appendix to Spiro, Jones, and Wark, Infrared Phys. 5, 11 (1965). 1 8P. Beckmann and A. Spizzichino, The Scattering of Electro- magnetic Waves from Rough Surfaces (Macmillan, New York, 1963), p.88. "D. B. Judd, J. Opt. Soc. Am. 57, 445 (1967).
    分享到：
    赞 收藏

    相关推荐

    资料库

    游戏开发

    共收录170份资料，累计3个分类，关注成员有19位，主要包括：cocos2D,其他,Unity3D

    热门标签

    cocos2D 其他 Unity3D

    最新资料