logo资料库

复合衰落信道下分布式MIMO系统中断概率及信道容量分析_彭文杰.pdf

发布时间：2022-06-16 发布人：admin 分类：说明书 资料大小：1.34M 资料格式：pdf 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    2015年2月 Journal on Communications February 2015 2015052-1 第36卷第2期 通 信 学 报 Vol.36 No. 2复合衰落信道下分布式MIMO系统中断概率及信道容量分析 彭文杰，李岳衡，薛团结，居美艳，黄平 (河海大学 计算机与信息学院，江苏 南京 211100) 摘 要：针对分布式MIMO系统中断概率和信道容量这2大性能指标，在复合衰落信道模型下，当上行链路采用最大比发送—选择合并，下行链路采用选择发送—最大比合并时，利用Lognormal分布对复杂Gamma-Lognormal分布的近似，推导得到当移动台位置给定时，系统中断概率和信道容量的闭合表达式，证明了系统性能指标与移动台分布之间存在密切的联系；随后依照实际通信环境，提出一种考虑存在小区热点的移动台非均匀分布模型，然后推导得到考虑该分布模型后的系统平均中断概率和平均信道容量闭合表达式；最后通过计算机仿真，证明了所提近似处理的精确性以及各项理论分析的合理性。 关键词：分布式MIMO；复合衰落信道；中断概率；信道容量；移动台分布 中图分类号：TN929.5 文献标识码：A Outage probability and capacity analysis of distributed MIMO systems over a composite fading channel PENG Wen-jie, LI Yue-heng, XUE Tuan-jie, JU Mei-yan, HUANG Ping (College of Computer and Information, Hohai University, Nanjing 211100, China) Abstract: The exact closed-form expressions about the outage probability and capacity of distributed MIMO systems over a composite fading channel are derived firstly by using Lognormal approximation to complicated Gamma-lognormal distribution when mobile station (MS) in the cell is fixed at some position and the so-called maximum ratio transmis-sion/selected combining (MRT-SC) and selected transmission/maximum ratio combining (ST-MRC) schemes are adopted in uplink and downlink respectively. Then based on a newly proposed non-uniform MS cell distribution model, which is more consistent with the MS cell hotspot distribution in an actual communication environment, the average outage prob-ability and capacity formulas synthesizing the MS cell position information are further derived. Finally, the accuracy of the approximation method and the rationality of the corresponding theoretical analysis about the system performance are proven and illustrated by computer simulations. Key words: distributed MIMO; composite fading channel; outage probability; capacity; MS distribution 1 引言 为解决现代无线通信系统中广大用户对通信质量和传输速率越来越高的需求与有限带宽之间的矛盾，分布式MIMO系统以其独特的技术架构而受到了越来越多科技工作者的关注。由于分布式MIMO系统充分利用了空间微分集与宏分集增益[1]，能在不增加系统分配频段的前提下成倍提高系统容量的同时，亦展现出可有效地提高各对收发链路之间的可靠性、降低系统功耗以及提高无线信号覆盖能力等的巨大优势[2]，故已被列为面向未来B4G/5G无线通信系统的备选方案之一[3]。不过在分布式MIMO系统投入到未来实际应用之前，从系统上层网络规划的角度而言，设计者将面临着诸如天线端口选址、系统无线资源分配等诸多设计挑战；而中断概率和信道容量作为涉及分布式MIMO系统上层网络规划的两项重要性能指标，对整个系统参数的优化设计具有极其重要的指导价值，因此开收稿日期：2014-03-17；修回日期：2014-11-09 基金项目：江苏省教育厅高校科研成果产业化推进基金资助项目（JHB2012-4） Foundation Item: The College Industrialization Project of Jiangsu Province (JHB2012-4) doi:10.11959/j.issn.1000-436x.2015052
    通 信 学 报 第36卷 2015052-2 展对中断概率和信道容量的理论分析就显得尤为重要。 文献[1]最早利用接收信噪比的概率密度函数证明了分布式MIMO系统在信道容量方面较传统集中式MIMO系统的巨大优越性，但仅给出仿真数据而没有给出闭合数学表达式，分析的理论性与严谨性有待深入。文献[4]在Nakagami-m信道下，综合考虑阴影衰落和路径损耗，研究了系统上行信道的中断概率，但作者假设移动台仅有一根天线，显然不符合MIMO系统的多天线传输特征，故分析不具有完备性与通用性。文献[5]研究了系统下行信道的中断概率，接收端虽采用多天线，但文中小尺度衰落却采用的是传统Rayleigh衰落，此模型并不能真实反映现代城市通信环境中衰落的客观实际。文献[6]同样也只采用了Rayleigh衰落模型，利用高斯随机变量对交互信息做近似，得到了分布式MIMO系统小区中断概率的闭合表达式，但这种近似对基站数目有区分，即基站数目不同时，得到的中断概率表达式也不同，显然这种近似的通用性受到了限制。虽然文献[7]也注意到文献[5]采用Rayleigh分布作为小尺度衰落的缺陷而在复合衰落信道模型下利用数学近似给出了下行信道容量的闭合表达式，但也只考虑移动台配置了一根天线的简单情形。 此外，上述所有文献中都没有考虑小区移动台分布对系统中断概率的影响（这个结论作为本文的一个重要观点与贡献，其理论依据将在下文给出）。鉴于上述文献在分析分布式MIMO系统性能方面存在的各种不足或缺陷，本文在充分研究与分析前人研究成果的基础上，拟综合考虑复合衰落信道模型和移动台用户分布可能对分布式MIMO系统性能的影响，并在移动台配置多根天线的条件下依据合理的数学推导给出系统性能指标中断概率和信道容量的闭型或近似表达，以完善对分布式MIMO系统性能分析方面的理论研究。 2 系统建模 如图1所示，一个简单的分布式MIMO系统配有K个天线端口，根据需要放置在小区内的各个不同位置上，并通过光纤连接到主处理机（MPU）。在直角坐标系下，端口位置记作(,)iixy，1,2,,iK；小区内移动台MS，配有L根天线，其在小区内位置记作(,)xy。 图1 分布式MIMO系统示意 在正式介绍分布式MIMO系统小区上下行传输机制之前，此处先就本文之所以选择简单单移动用户来建模并分析相关问题的出发点做简要介绍。需要补充说明的是，在实际通信环境中小区内肯定是存在多个通信用户的，这些多个用户在与基站端口天线实施通信过程中必然会导致对上行信号在某个基站端口接收端或者下行信号在某个用户接收端产生干扰，即产生所谓小区内的多用户间干扰。为解决这个问题，在诸如3G/4G的现代通信系统中，普遍采用频分多址、时分多址或者码分多址方案中的一种或者组合来加以克服。当采用频分或时分多址技术时，可以为身处同一小区内的不同用户分配不同的频段或时隙以抑制用户间的干扰实现共同通信；而采用码分多址技术时则可利用为不同用户分配不同的伪随机序列的方式来区分用户。当然在采用码分多址技术时，由于多径传输效应，即便是初始完全正交设计的扩频序列在系统解扩时也不可避免地会产生多址干扰和码间干扰；不过前人的研究结果表明[8,9]，无论在接收端是否采用多址干扰抑制技术，这部分未经干扰抑制的因多径效应产生的多址干扰和码间干扰，乃至经过干扰抑制技术后产生的干扰残差都可以从理论上近似为加性高斯噪声，进而通过归入背景噪声来加以处理。这种处理在简化问题分析的同时，并不会对下文基于接收信噪比概率密度函数推导的系统中断概率和系统容量的分析造成影响。 正是在这样的背景下，根据经典分布式MIMO系统的工作机理及简化问题分析的需要，本文仅选取单用户即一个移动台的特例进行建模处理。而在具体的系统上行链路收发方案设计中，移动台拟采用最大比发送（MRT）技术[10]，以此获得最大输出信噪比；网络侧分布式天线端口则采用选择合并（SC），即选择增益最大的信道建立通信链路。而
    第2期 彭文杰等：复合衰落信道下分布式MIMO系统中断概率及信道容量分析 2015052-3 下行链路中，网络侧天线端口则采用选择发送（ST），移动台采用最大比合并（MRC）。 另一点需要补充说明的是，在上述分布式MIMO系统收发方案的建模过程中，之所以在上行链路采用MRT-SC，下行采用ST-MRC，也就是在上下行链路中网络侧都采用选择分集（即依据信道优劣选择一个天线端口与移动台建立通信链路进行数据传输），而不是像有些研究分布式MIMO的文献中所采用的全天线端口皆同时参与收发的全通信（BT）模式[11]，两相比较，本文所提出并加以研究的选择通信模型一方面工作机制更为简单，可以在天线端口本身就已于小区中分开放置的分布式MIMO系统中有效减小移动台的平均接入距离、降低收发功耗，最大程度地利用分布式端口的设计优势[1]；另一方面，也可避免全通信模型下因基站端口天线相隔较远导致的传输延时对目标移动用户接收信号以及其他小区用户信号造成的不必要干扰。此外，在用户侧移动台端采用MRT与MRC技术，而不是MIMO系统中广受关注的空时分组编码技术，这是因为虽然空时分组编码技术被认为能够提高MIMO系统性能，但在未来大规模MIMO系统中，天线阵规模将十分庞大，采用空时分组编码将会导致编码的设计和解码复杂度的急剧增加；另一重要原因还在于，文献[12]的研究结果表明，当且仅当发送天线数目为2根时，系统采用空时分组编码能够获得的输出信噪比最大，而此时的系统输出信噪比仍然低于系统采用最大比合并技术时能够获得的输出信噪比。 综合上述分析不难看出：本文提出并加以研究的上行采用MRT-SC，下行采用ST-MRC的系统模型能够充分挖掘MIMO技术在系统中断概率和信道容量方面的潜力，凸显分布式MIMO系统的性能优势。 2.1 上行MRT-SC 首先考虑系统上行链路。假设移动台完全已知信道信息；为简化分析并进一步约束天线之间的信道为准静态平坦衰落，且系统噪声受限。令(1,2,,)jihjL表示移动台第j根天线与天线端口iAP之间的信道复增益，移动台发送功率为E；假设移动台所有天线同时向所有天线端口发送信息符号x，符号能量归一化，则在MRT方案中，符号x乘以相位旋转因子*()jjjiiibhh后，以功率jiG发送。 221ELjjjiiijGhh (1) 天线端口iAP接收到的信号可以表示为 211ELLjjjjiiiiijjyhGbxzhxz (2) 其中，z为高斯噪声，均值为0，方差为0N。 综合考虑Nakagami-m衰落、阴影衰落和路径损耗，将jih建模为 jjjiiihgS (3) 其中，jig代表移动台第j根天线与天线端口iAP之间的小尺度衰落。由于系统中各端口分开放置，所以jig(1,2,,)iK相互独立，但不同天线端口对应的小尺度衰落不一定同分布；而移动台尺寸受限，使其各根天线上信号到达同一个天线端口时所经历的衰落基本相同，因此jig的分布与移动台上的天线无关，只与天线端口的选择有关，所以将其建模成服从参数为im的Nakagami-m分布[12]。 jiS代表相应信道的阴影衰落。假设移动台每根天线的信号经历相同的阴影衰落，即 12LiiiiSSSS (4) 阴影衰落服从对数正态分布，iS概率密度函数[12]为 22(10lg)()exp2π2iiSiisfss (5) 其中，10ln10，i和i分别是10lgiS的均值和标准差，以dB为单位。而均值i的取值与路径损耗有关[14]，通常可以建模为 010lg()iidd (6) 其中，0d为参考距离，是路径损耗指数，id是移动台与天线端口iAP的间距，直角坐标系下可表示为 22()()iiidxxyy (7) 根据上述建模，端口iAP上的接收信噪比为 22011ELLjjiiiijjhgN (8) 其中，0iiESN。 由于iS服从对数正态分布，因此i也服从对数正态分布，其概率密度函数可表示为
    通 信 学 报 第36卷 2015052-4 22(10lg)()exp2π2iiiif (9) 其中，010lg()iiEN，是10lgi的均值，10lgi的方差仍然为2i。 在式(8)中，记2jjiiig，在i已知的前提下，ji的条件概率密度函数为 1exp()iijiiimmiimimrmrfrwwwm (10) 根据矩生成函数的定义，可以得到ji的条件矩生成函数为[12] 0ed1ijjiiiimpripMpfrwrm (11) 由于jig(1,2,,)iK相互独立，所以ji之间也相互独立，此时可以得到i的条件矩生成函数 11ijiiiiLmLijpMpMpm (12) 将矩生成函数中的变量p取反，能够得到与其相应的概率密度函数取拉普拉斯变换的数学表达式[12]，即 iiiifrMp (13) 其中，()表示拉普拉斯变换。将式(12)代入上式(13)后，利用文献[15]中表17.13的式(26)得 1evvaxxvsa (14) 可以得到i的条件概率密度函数 1exp()iiiiiLmLmiiLmimrmrfrLm (15) 其中，()为伽马函数。 最后对i进行积分运算就可以得输出信噪比i的无条件概率密度函数 01022()()dexp()10lgexpd2π2iiiiiiiLmLmiiLmiiiifrfrfmrmrLm (16) 从上述表达式可以看出，此时天线端口iAP的接收信噪比服从Gamma-Lognormal分布[12]。 基站侧各端口采用选择合并机制，以获得最大的输出信噪比 12max,,,K (17) 2.2 下行ST-MRC 下行链路中，所有天线端口以功率E发送信息符号x，则移动台各天线上接收到来自天线端口iAP的信号矢量为 T12E,,,Liiiihhhxyz (18) 其中，z为噪声矢量，其各元素是相互独立的高斯随机变量，均值为0，方差为0N。 在与上行链路相同的信道环境下，移动台采用最大比合并，此时来自天线端口iAP的接收信噪比为 22011EjLLijiiijjhgN (19) 下行链路基站侧采用选择发送机制，其目的也是为了接收端获得最大输出信噪比 12max,,,K (20) 对式(8)、式(17)和式(19)、式(20)进行对比发现，不管是上行链路还是下行链路，最终系统的输出信噪比是相同的，因此在上行采用MRT-SC机制，下行采用ST-MRC机制时，上下行链路基于最大输出信噪比的分析是完全等效的。 2.3 概率密度函数数学近似 式(16)给出了系统输出信噪比i的概率密度函数。从该表达式可以看出，这是一个复杂的无穷积分，不利于后续对系统中断概率、信道容量的研究分析。而Gordon的研究[16]表明，Lognormal分布可以很好地近似Gamma-lognormal分布，所以根据这一成果对式(16)做近似处理，得到输出信噪比i的概率密度函数 ˆ2πiifrr22ˆ10lgexpˆ2iir (21) 其中，ˆi和ˆi分别表示近似后的Lognormal分布的均值与标准差，以dB为单位，与原本Gamma- lognormal分布的均值与标准差的关系为 022ˆ10lgElnˆ2,iiiiiiiNLmmLm (22)
    第2期 彭文杰等：复合衰落信道下分布式MIMO系统中断概率及信道容量分析 2015052-5 其中，()为digamma函数[17]，(,)为Riemann zeta函数[15]，式(22)的推导过程中，利用了文献[15]中的式(4.352.1)和式(4.358.2)。 由式(21)可以进一步得到系统输出信噪比的累积分布函数为 0ˆ10lg1()()d1erfc2ˆ2iiXiiXFXfrr (23) 其中，erfc()为互补误差函数。 根据前文分析，因各个天线端口所对应的接收信噪比i之间相互独立，由式(20)和式(23)可推导得到系统最终输出信噪比的累积分布函数与各天线端口i的累积分布函数之间存在如下关系 1211()Pr{}Pr{,,,}ˆ10lg11erfc2ˆ2iKKKiiiiFrrrrrrFr (24) 其中，Pr{}表示求概率。 3 系统性能分析 3.1 特定位置系统性能分析 分布式MIMO系统中断概率定义为系统输出信噪比低于某一数值时的概率。在本文中，鉴于上下行接收信噪比的等价性，故不失一般性，以上行链路为例，此时的中断概率可以表示为 thoutth1ˆ10lg11erfc2ˆ2KiiiPF (25) 其中，th是信噪比门限值。 对式(24)求导可以得到的概率密度函数为 '1ijKKijifrFrfrFr 21ˆ10lgexpˆ2πKiiirr ˆ10lg11erfc2ˆ2Kjjijr (26) 根据香农信息论，信道遍历容量的表达式为 0lb1()dCrfrr (27) 将式(26)代入式(27)之后得到的表达式为复杂的无穷积分，不能直接获得数值解，可以通过Gauss- Hermite积分公式[17]将其简化为 ˆ210111lb110πˆ211erfc2ˆ2intKNninKinjijCHt (28) 其中，N是Hermite多项式的阶数，nt和nH分别是N阶Hermite多项式的基点和权重，可以通过查询文献[17]表25.10得到。 至此，式(25)与式(28)分别给出了分布式MIMO系统特定位置处的中断概率和信道容量的闭合表达式，从该二闭合表达式可以直观地观测网络系统中各个物理因素对这两项性能指标的影响。 需要注意的是：在分布式MIMO系统中，当各个天线端口位置确定，即运营商在布网结束之后，上述数学表达式所代表的性能指标所能达到的数值与移动台在所属区域内的位置密切相关。这是因为，不管是中断概率还是信道容量，其表达式中的ˆi实际上是以移动台坐标(,)xy为参变量的函数，当移动台坐标变化时，两项性能指标得到的数值也会随之变化，所以传统意义上的中断概率和信道容量并不能完全反映网络的物理实质；即使是完全相同的2个系统，在移动台分布不同的情况下，也会测得不同的系统中断概率和信道容量。所以，当中断概率和信道容量作为系统评估的目标时，还必须充分考虑移动台在小区内的地理分布特征所带来的影响。 3.2 小区平均位置系统性能分析 3.2.1 移动台分布模型 考虑到分布式MIMO系统组网灵活的特点，本文拟应用一种方形而非传统文献中常见的圆形小区规划策略。已有文献研究结果表明，方形小区的划分配合合理的调配方案，可以有效地减小小区间干扰，提高系统性能[18]。事实上，方形小区与圆形小区在理论分析过程中并无本质上的区别，仅建模时所选坐标系有差异：适用于方形小区的正交直角坐标系相较于圆形小区采用的极坐标更为简单；同时在方形小区划分下，引入低能耗的扇形天线更为便利，这也从一个侧面体现了分布式MIMO系统通过灵活组网以进一步减小小区间相互干扰的优点。 如图2所示，4个扇形天线端口便可围成一个方形小区，在足够广的区域内，所有的天线端口都ˆiˆiˆj2ˆ2i
    通 信 学 报 第36卷 2015052-6 与同一个主处理单元相连，由该主处理单元负责天线端口的调度分配工作。 图2 移动台分布 在以往涉及小区内移动台分布的文献中，移动台大都被建模为均匀分布，即移动台出现在小区内任意位置的概率是相同的。以方形小区为例，若边长为D，在直角坐标系下，其概率密度函数定义为 2(,)1fxyD (29) 不过在实际应用环境中，移动台在小区内的分布显然要复杂得多，也不会简单地服从均匀分布。一般来说，移动台的地理分布特征是不可预期的；但是，如果从小区上层网络规划的角度来分析，基站应该放置于移动台分布较密集的地区，或者说移动台会更多地分布在基站周围。基于此考虑，再结合实际通信环境中常出现的小区热点，即存在某一区域内移动台的数量相较于其他区域明显偏多的现象，本文将每个以基站端口天线为圆心，r为半径的圆形区域定义或移动台分布密集区，即所谓小区热点区域；在该圆形区域内，移动台的分布十分密集，而其余区域的移动台分布则相对稀疏。考虑图2所标注的单个方形区域，区域1为4个扇形天线所分别覆盖的4个1/4圆，表示移动台分布密集区，记作1A；区域2为方形小区中除去1A外的剩余区域，记作2A，其内移动台分布相对稀疏。定义移动台在该方形小区区域内分布的概率密度函数为 12222, (,)π(,)1, (,)πxyArfxyxyADr (30) 其中，0,1，表示移动台位于区域1内的概率。按照前文分析，如果存在小区热点，其数值理应满足22πrD，而当22πrD时，整个区域内的移动台服从均匀分布。在上式中，及圆形半径r的取值是可变的，不同的数值将代表不同的移动台分布情况，因此本文提出的分布模型具备很强的灵活性。 3.2.2 平均中断概率及平均信道容量 根据3.1节的分析，式(25)和式(28)得到的是移动台位于小区某一给定位置处分布式MIMO系统中断概率和信道容量的表达式，显然如果依此来评估整个系统的性能将会因所得结果随用户具体位置变化而带有很大的局限性。因此，较合理的评估办法应该是充分考虑移动台的整体分布情况，也即对不同地理位置上的移动台所分别对应的系统中断概率和信道容量进行概率加权估算，最终获到整个系统的平均性能指标。 对式(25)取均值获得系统的平均中断概率为 out(,)outout00E(,)(,)ddDDxyPPPxyfxyxy (31) 对式(28)取均值能够获得系统平均信道容量为 (,)00E(,)(,)ddDDxyCCCxyfxyxy (32) 其中，(,)fxy为移动台在小区内的分布概率密度函数，定性分析时，它可以表示任意移动台地理分布特征，不仅仅局限于本文3.2.1节所提到的均匀分布或存在小区热点的非均匀分布。由于现实中移动台的分布往往较为复杂，因此上述二重积分会很难处理，最终可能得不到解析表达式。 为解决这一难题，本文引入Simpson二重积分公式[19]，对式(31)和式(32)进行处理，结合前文的推导，最终得到系统平均中断概率为 out,out00,,9QPpqpqpqpqhkPaPxyfxy (33) 系统平均信道容量为 ,00,,9QPpqpqpqpqhkCaCxyfxy (34) 其中，P和Q分别是横坐标和纵坐标等距划分的节点数，取值都必须为偶数，hDP，kDQ，pxph，qyqk；,pqa为权值，是权值矩阵A中第1p行，第1q列元素，权值矩阵A由下式给出 T111 4 2 4 2 4 11 4 2 4 2 4 1PQA (35)
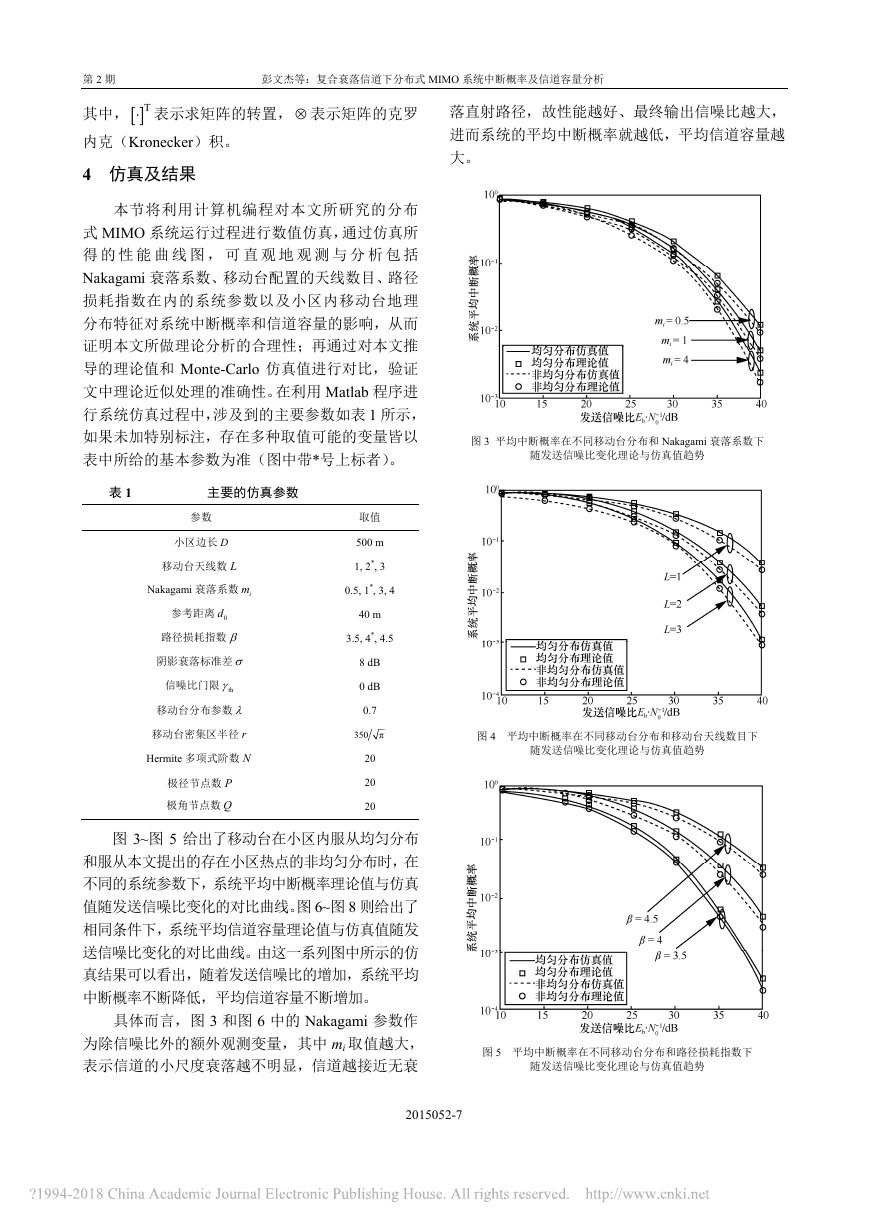
    第2期 彭文杰等：复合衰落信道下分布式MIMO系统中断概率及信道容量分析 2015052-7 其中，T表示求矩阵的转置，表示矩阵的克罗内克（Kronecker）积。 4 仿真及结果 本节将利用计算机编程对本文所研究的分布式MIMO系统运行过程进行数值仿真，通过仿真所得的性能曲线图，可直观地观测与分析包括Nakagami衰落系数、移动台配置的天线数目、路径损耗指数在内的系统参数以及小区内移动台地理分布特征对系统中断概率和信道容量的影响，从而证明本文所做理论分析的合理性；再通过对本文推导的理论值和Monte-Carlo仿真值进行对比，验证文中理论近似处理的准确性。在利用Matlab程序进行系统仿真过程中，涉及到的主要参数如表1所示，如果未加特别标注，存在多种取值可能的变量皆以表中所给的基本参数为准（图中带*号上标者）。 表1 主要的仿真参数 参数 取值 小区边长D 500 m 移动台天线数L 1, 2*, 3 Nakagami衰落系数im 0.5, 1*, 3, 4 参考距离0d 40 m 路径损耗指数 3.5, 4*, 4.5 阴影衰落标准差 8 dB 信噪比门限th 0 dB 移动台分布参数 0.7 移动台密集区半径r 350π Hermite多项式阶数N 20 极径节点数P 20 极角节点数Q 20 图3~图5给出了移动台在小区内服从均匀分布和服从本文提出的存在小区热点的非均匀分布时，在不同的系统参数下，系统平均中断概率理论值与仿真值随发送信噪比变化的对比曲线。图6~图8则给出了相同条件下，系统平均信道容量理论值与仿真值随发送信噪比变化的对比曲线。由这一系列图中所示的仿真结果可以看出，随着发送信噪比的增加，系统平均中断概率不断降低，平均信道容量不断增加。 具体而言，图3和图6中的Nakagami参数作为除信噪比外的额外观测变量，其中mi取值越大，表示信道的小尺度衰落越不明显，信道越接近无衰落直射路径，故性能越好、最终输出信噪比越大，进而系统的平均中断概率就越低，平均信道容量越大。 图3 平均中断概率在不同移动台分布和Nakagami衰落系数下 随发送信噪比变化理论与仿真值趋势 图4 平均中断概率在不同移动台分布和移动台天线数目下 随发送信噪比变化理论与仿真值趋势 图5 平均中断概率在不同移动台分布和路径损耗指数下 随发送信噪比变化理论与仿真值趋势
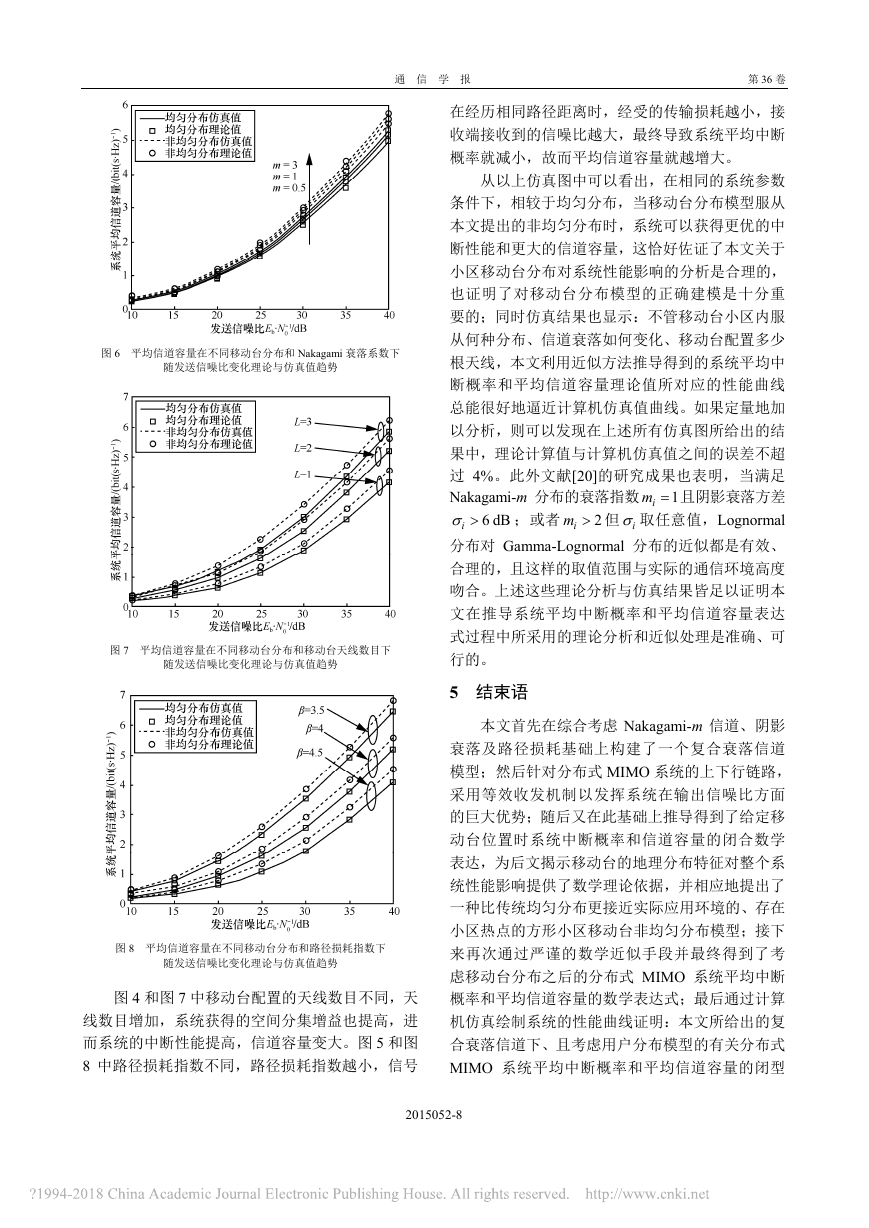
    通 信 学 报 第36卷 2015052-8 图6 平均信道容量在不同移动台分布和Nakagami衰落系数下 随发送信噪比变化理论与仿真值趋势 图7 平均信道容量在不同移动台分布和移动台天线数目下 随发送信噪比变化理论与仿真值趋势 图8 平均信道容量在不同移动台分布和路径损耗指数下 随发送信噪比变化理论与仿真值趋势 图4和图7中移动台配置的天线数目不同，天线数目增加，系统获得的空间分集增益也提高，进而系统的中断性能提高，信道容量变大。图5和图8中路径损耗指数不同，路径损耗指数越小，信号在经历相同路径距离时，经受的传输损耗越小，接收端接收到的信噪比越大，最终导致系统平均中断概率就减小，故而平均信道容量就越增大。 从以上仿真图中可以看出，在相同的系统参数条件下，相较于均匀分布，当移动台分布模型服从本文提出的非均匀分布时，系统可以获得更优的中断性能和更大的信道容量，这恰好佐证了本文关于小区移动台分布对系统性能影响的分析是合理的，也证明了对移动台分布模型的正确建模是十分重要的；同时仿真结果也显示：不管移动台小区内服从何种分布、信道衰落如何变化、移动台配置多少根天线，本文利用近似方法推导得到的系统平均中断概率和平均信道容量理论值所对应的性能曲线总能很好地逼近计算机仿真值曲线。如果定量地加以分析，则可以发现在上述所有仿真图所给出的结果中，理论计算值与计算机仿真值之间的误差不超过4%。此外文献[20]的研究成果也表明，当满足Nakagami-m分布的衰落指数1im且阴影衰落方差6dBi；或者2im但i取任意值，Lognormal分布对Gamma-Lognormal分布的近似都是有效、合理的，且这样的取值范围与实际的通信环境高度吻合。上述这些理论分析与仿真结果皆足以证明本文在推导系统平均中断概率和平均信道容量表达式过程中所采用的理论分析和近似处理是准确、可行的。 5 结束语 本文首先在综合考虑Nakagami-m信道、阴影衰落及路径损耗基础上构建了一个复合衰落信道模型；然后针对分布式MIMO系统的上下行链路，采用等效收发机制以发挥系统在输出信噪比方面的巨大优势；随后又在此基础上推导得到了给定移动台位置时系统中断概率和信道容量的闭合数学表达，为后文揭示移动台的地理分布特征对整个系统性能影响提供了数学理论依据，并相应地提出了一种比传统均匀分布更接近实际应用环境的、存在小区热点的方形小区移动台非均匀分布模型；接下来再次通过严谨的数学近似手段并最终得到了考虑移动台分布之后的分布式MIMO系统平均中断概率和平均信道容量的数学表达式；最后通过计算机仿真绘制系统的性能曲线证明：本文所给出的复合衰落信道下、且考虑用户分布模型的有关分布式MIMO系统平均中断概率和平均信道容量的闭型
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料