IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS—II: EXPRESS BRIEFS, VOL. 65, NO. 11, NOVEMBER 2018 1579 A 45-μW, 162.1-dBc/Hz FoM, 490-MHz Two-Stage Differential Ring VCO Without a Cross-Coupled Latch Oh-Yong Jung , Hyun-Gi Seok, Anjana Dissanayake, and Sang-Gug Lee, Member, IEEE Abstract—An ultra-low-power, start-up and phase noise performance improved 2-stage differential ring voltage-controlled oscillator (VCO) is proposed. The proposed delay cell archi- tecture reduces power consumption by eliminating the cross- coupling latch of the conventional ring VCO. Instead of the latch, the inverters in the proposed delay cell produce negative conductance by insertion of an additional RC network, which improves the start-up performance of the proposed VCO. The proposed delay cell architecture also improves the phase noise performance of the VCO as it sharpens the drain current of the inverter stage such that it resembles an impulse waveform, which reduces the root-mean-square value of impulse sensitiv- ity function. Implemented in a 65-nm CMOS technology, the measured phase noise of the proposed VCO at 1 MHz offset is −94.84 dBc/Hz at 490 MHz oscillation frequency while dis- sipating 45 µW from a 0.6-V supply. The figure of merit is 162.1 dBc/Hz. Index Terms—Ring oscillator, differential VCO, 2-stage VCO, low phase noise VCO, ultra low power (ULP). I. INTRODUCTION W ITH increasing need for battery-based radio utilized in the Internet of Things (IoT) and healthcare applica- tions, there is currently strong demand to develop ultra-low power (ULP) transceivers. In low power transceivers such as Ultra-wideband (UWB) radios [1], [2] and MedRadio [3], due to their relaxed phase noise requirements, ring VCOs have been adopted as a power-efficient solution for the local oscil- lator (LO). For ring VCOs, a differential architecture with an even number of stages is an attractive choice due to the available quadrature signals. Since the minimum number of differential stages is two, a 2-stage differential ring VCO is a candidate for ULP implementation. Due to the difficulties in start-up, previous studies on 2- stage ring VCOs have focused on a start-up analysis based on Barkhausen criteria [1], [4], [5]. Previous works [1], [4] have suggested that inserting a cross-coupled MOSFET as a latching circuit inside a differential delay cell is essential to generate negative conductance for robust start-up and the Manuscript received July 27, 2017; accepted October 21, 2017. Date of publication October 26, 2017; date of current version October 29, 2018.This work was supported by the National Research Foundation of Korea through the Korean Government under Project NRF-2015R1A5A1036133. This brief was recommended by Associate Editor N. M. Neihart. (Corresponding author: Oh-Yong Jung.) authors are with the Department of Electrical Engineering, Korea Advanced Institute of Science and Technology, Daejeon 305-701, South Korea (e-mail: id1232@kaist.ac.kr). The Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org. Digital Object Identifier 10.1109/TCSII.2017.2766674 1549-7747 c 2017 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See http://www.ieee.org/publications_standards/publications/rights/index.html for more information. Fig. 1. system model. 2-stage differential ring VCO (a) block diagram and (b) feedback other [5] explains that the latch generates extra delay to sat- isfy the phase requirement. With ULP design, however, the adoption of cross-coupled latch brings the issue of additional power dissipation. This brief reports a differential delay cell architecture that generates negative conductance without requiring the cross- coupled latch. Section II explains the principle for improving the start-up and phase noise performance of the 2-stage VCO that adopts the proposed delay cell. Section III reports measurement results of the VCO and Section IV concludes. II. VCO ANALYSIS A. Start-Up Analysis Fig. 1 shows a 2-stage ring VCO block diagram and a feedback system model. According to [4], an oscillator can oscillate if complex-conjugate poles of the closed-loop transfer function (TF) of the oscillator are in the right half plane (RHP) 

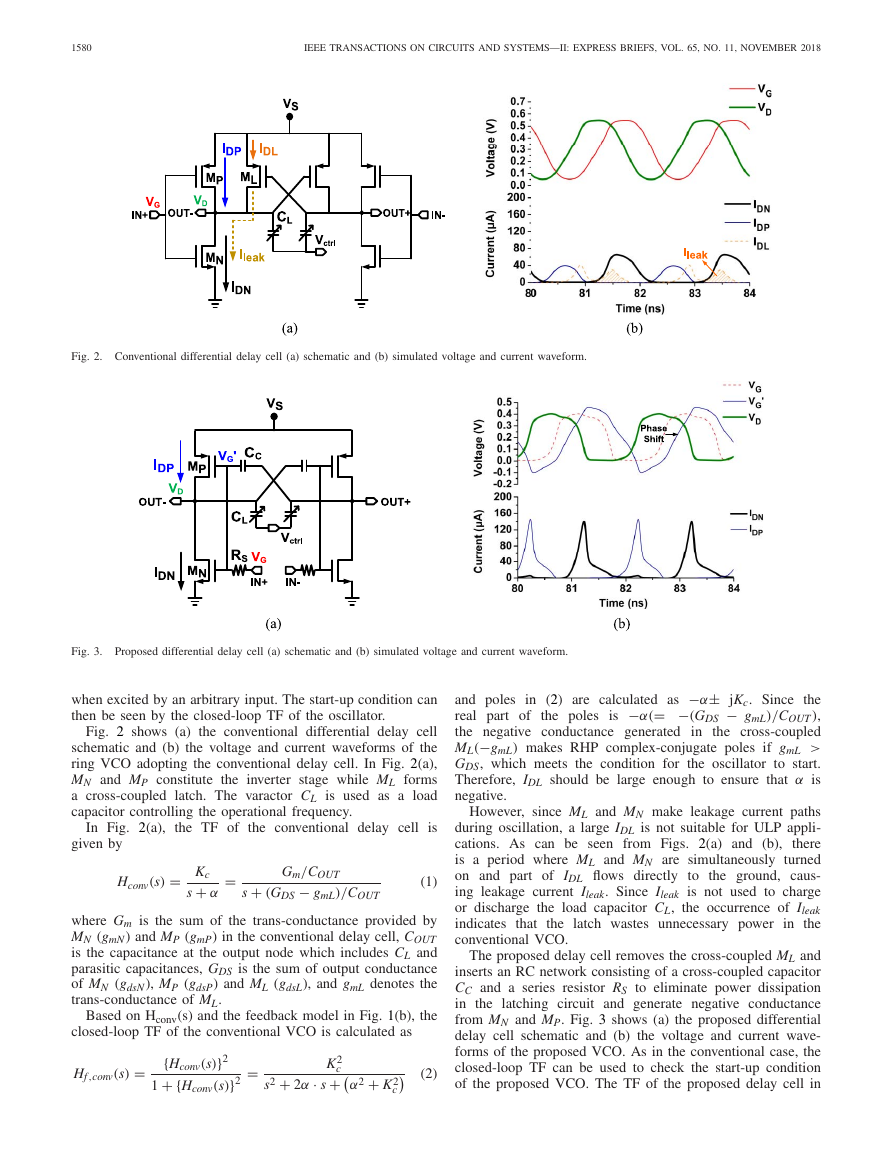
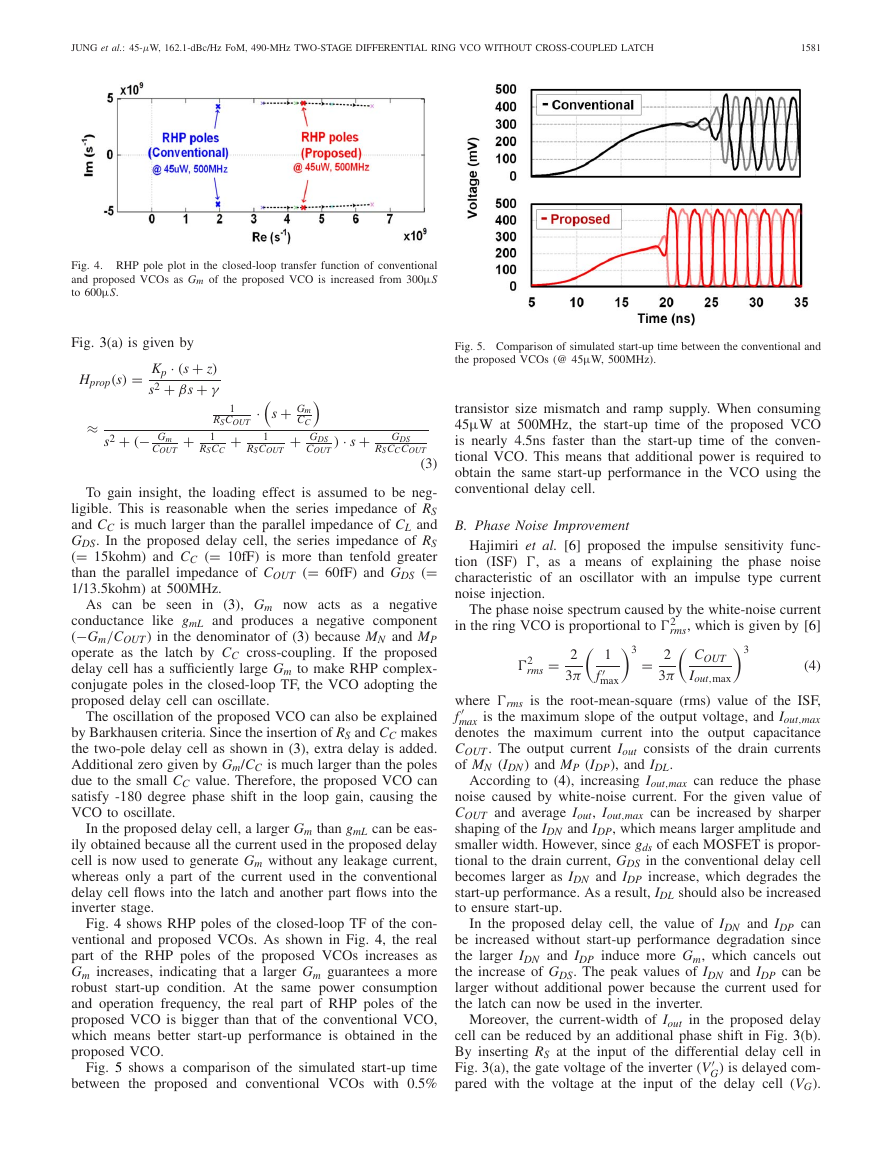
1580 IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS—II: EXPRESS BRIEFS, VOL. 65, NO. 11, NOVEMBER 2018 Fig. 2. Conventional differential delay cell (a) schematic and (b) simulated voltage and current waveform. Fig. 3. Proposed differential delay cell (a) schematic and (b) simulated voltage and current waveform. when excited by an arbitrary input. The start-up condition can then be seen by the closed-loop TF of the oscillator. Fig. 2 shows (a) the conventional differential delay cell schematic and (b) the voltage and current waveforms of the ring VCO adopting the conventional delay cell. In Fig. 2(a), MN and MP constitute the inverter stage while ML forms a cross-coupled latch. The varactor CL is used as a load capacitor controlling the operational frequency. is In Fig. 2(a), the TF of the conventional delay cell given by Hconv(s) = Kc s + α = Gm/COUT s + (GDS − gmL)/COUT (1) where Gm is the sum of the trans-conductance provided by MN (gmN) and MP (gmP) in the conventional delay cell, COUT is the capacitance at the output node which includes CL and parasitic capacitances, GDS is the sum of output conductance of MN (gdsN), MP (gdsP) and ML (gdsL), and gmL denotes the trans-conductance of ML. Based on Hconv(s) and the feedback model in Fig. 1(b), the closed-loop TF of the conventional VCO is calculated as Hf ,conv(s) = {Hconv(s)}2 1 + {Hconv(s)}2 = K2 s2 + 2α · s + c α2 + K2 c (2) and poles in (2) are calculated as −α± jKc. Since the the poles is −α(= −(GDS − gmL)/COUT ), real part of the negative conductance generated in the cross-coupled ML(−gmL) makes RHP complex-conjugate poles if gmL > GDS, which meets the condition for the oscillator to start. Therefore, IDL should be large enough to ensure that α is negative. However, since ML and MN make leakage current paths during oscillation, a large IDL is not suitable for ULP appli- cations. As can be seen from Figs. 2(a) and (b), there is a period where ML and MN are simultaneously turned on and part of IDL flows directly to the ground, caus- ing leakage current Ileak. Since Ileak is not used to charge or discharge the load capacitor CL, the occurrence of Ileak indicates that the latch wastes unnecessary power in the conventional VCO. The proposed delay cell removes the cross-coupled ML and inserts an RC network consisting of a cross-coupled capacitor CC and a series resistor RS to eliminate power dissipation in the latching circuit and generate negative conductance from MN and MP. Fig. 3 shows (a) the proposed differential delay cell schematic and (b) the voltage and current wave- forms of the proposed VCO. As in the conventional case, the closed-loop TF can be used to check the start-up condition of the proposed VCO. The TF of the proposed delay cell in 

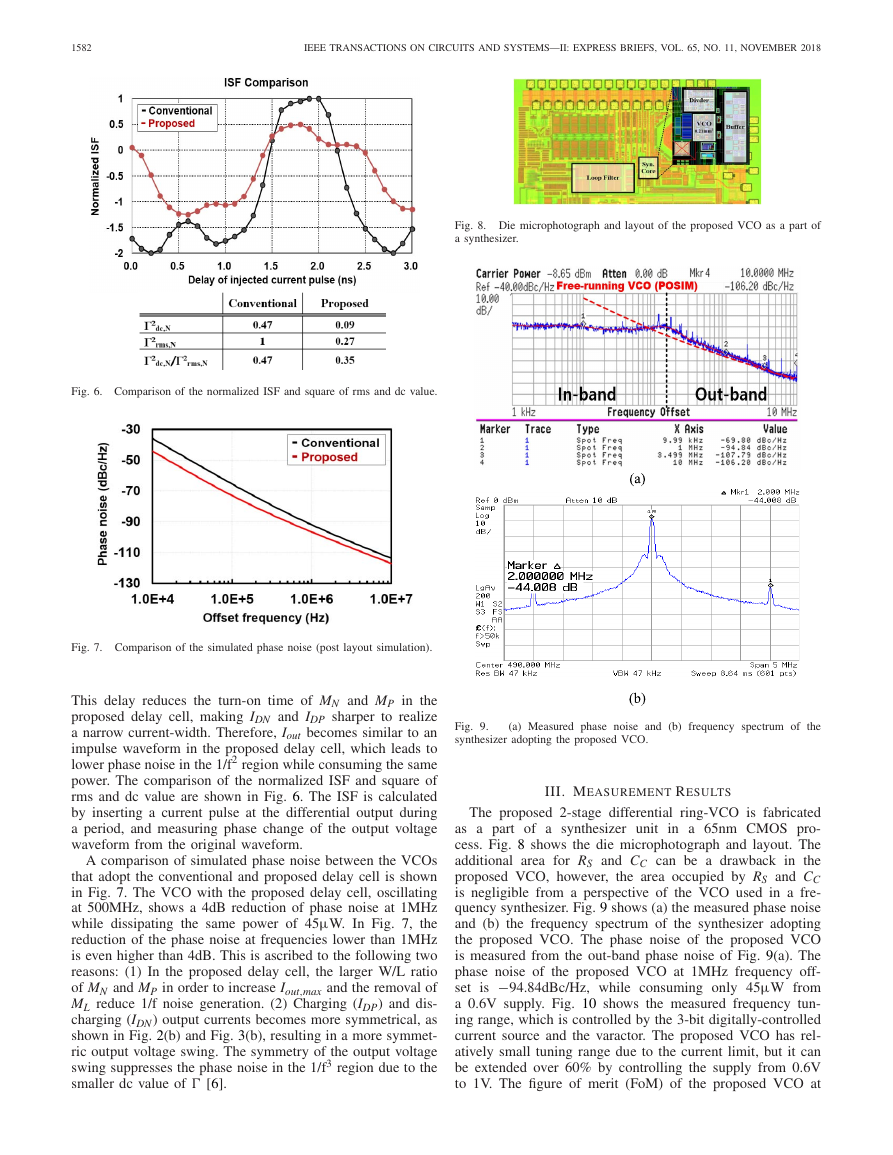
JUNG et al.: 45-μW, 162.1-dBc/Hz FoM, 490-MHz TWO-STAGE DIFFERENTIAL RING VCO WITHOUT CROSS-COUPLED LATCH 1581 Fig. 4. RHP pole plot in the closed-loop transfer function of conventional and proposed VCOs as Gm of the proposed VCO is increased from 300µS to 600µS. Fig. 3(a) is given by Hprop(s) = Kp · (s + z) s2 + βs + γ ≈ s2 + (− Gm + 1 RSCC COUT RSCOUT 1 · s + Gm + 1 RSCOUT CC + GDS COUT ) · s + GDS RSCCCOUT (3) To gain insight, the loading effect is assumed to be neg- ligible. This is reasonable when the series impedance of RS and CC is much larger than the parallel impedance of CL and GDS. In the proposed delay cell, the series impedance of RS (= 15kohm) and CC (= 10fF) is more than tenfold greater than the parallel impedance of COUT (= 60fF) and GDS (= 1/13.5kohm) at 500MHz. As can be seen in (3), Gm now acts as a negative conductance like gmL and produces a negative component (−Gm/COUT) in the denominator of (3) because MN and MP operate as the latch by CC cross-coupling. If the proposed delay cell has a sufficiently large Gm to make RHP complex- conjugate poles in the closed-loop TF, the VCO adopting the proposed delay cell can oscillate. The oscillation of the proposed VCO can also be explained by Barkhausen criteria. Since the insertion of RS and CC makes the two-pole delay cell as shown in (3), extra delay is added. Additional zero given by Gm/CC is much larger than the poles due to the small CC value. Therefore, the proposed VCO can satisfy -180 degree phase shift in the loop gain, causing the VCO to oscillate. In the proposed delay cell, a larger Gm than gmL can be eas- ily obtained because all the current used in the proposed delay cell is now used to generate Gm without any leakage current, whereas only a part of the current used in the conventional delay cell flows into the latch and another part flows into the inverter stage. Fig. 4 shows RHP poles of the closed-loop TF of the con- ventional and proposed VCOs. As shown in Fig. 4, the real part of the RHP poles of the proposed VCOs increases as Gm increases, indicating that a larger Gm guarantees a more robust start-up condition. At the same power consumption and operation frequency, the real part of RHP poles of the proposed VCO is bigger than that of the conventional VCO, which means better start-up performance is obtained in the proposed VCO. Fig. 5 shows a comparison of the simulated start-up time between the proposed and conventional VCOs with 0.5% Fig. 5. Comparison of simulated start-up time between the conventional and the proposed VCOs (@ 45µW, 500MHz). transistor size mismatch and ramp supply. When consuming 45µW at 500MHz, the start-up time of the proposed VCO is nearly 4.5ns faster than the start-up time of the conven- tional VCO. This means that additional power is required to obtain the same start-up performance in the VCO using the conventional delay cell. B. Phase Noise Improvement Hajimiri et al. [6] proposed the impulse sensitivity func- tion (ISF)
, as a means of explaining the phase noise characteristic of an oscillator with an impulse type current noise injection. in the ring VCO is proportional to
2 The phase noise spectrum caused by the white-noise current rms, which is given by [6] (4)
2 rms = 2 3π 3 = 2 3π 1 f max 3 COUT Iout,max where
rms is the root-mean-square (rms) value of the ISF, max is the maximum slope of the output voltage, and Iout,max f denotes the maximum current into the output capacitance COUT. The output current Iout consists of the drain currents of MN (IDN) and MP (IDP), and IDL. According to (4), increasing Iout,max can reduce the phase noise caused by white-noise current. For the given value of COUT and average Iout, Iout,max can be increased by sharper shaping of the IDN and IDP, which means larger amplitude and smaller width. However, since gds of each MOSFET is propor- tional to the drain current, GDS in the conventional delay cell becomes larger as IDN and IDP increase, which degrades the start-up performance. As a result, IDL should also be increased to ensure start-up. In the proposed delay cell, the value of IDN and IDP can be increased without start-up performance degradation since the larger IDN and IDP induce more Gm, which cancels out the increase of GDS. The peak values of IDN and IDP can be larger without additional power because the current used for the latch can now be used in the inverter. Moreover, the current-width of Iout in the proposed delay cell can be reduced by an additional phase shift in Fig. 3(b). By inserting RS at the input of the differential delay cell in Fig. 3(a), the gate voltage of the inverter (V G) is delayed com- pared with the voltage at the input of the delay cell (VG). 

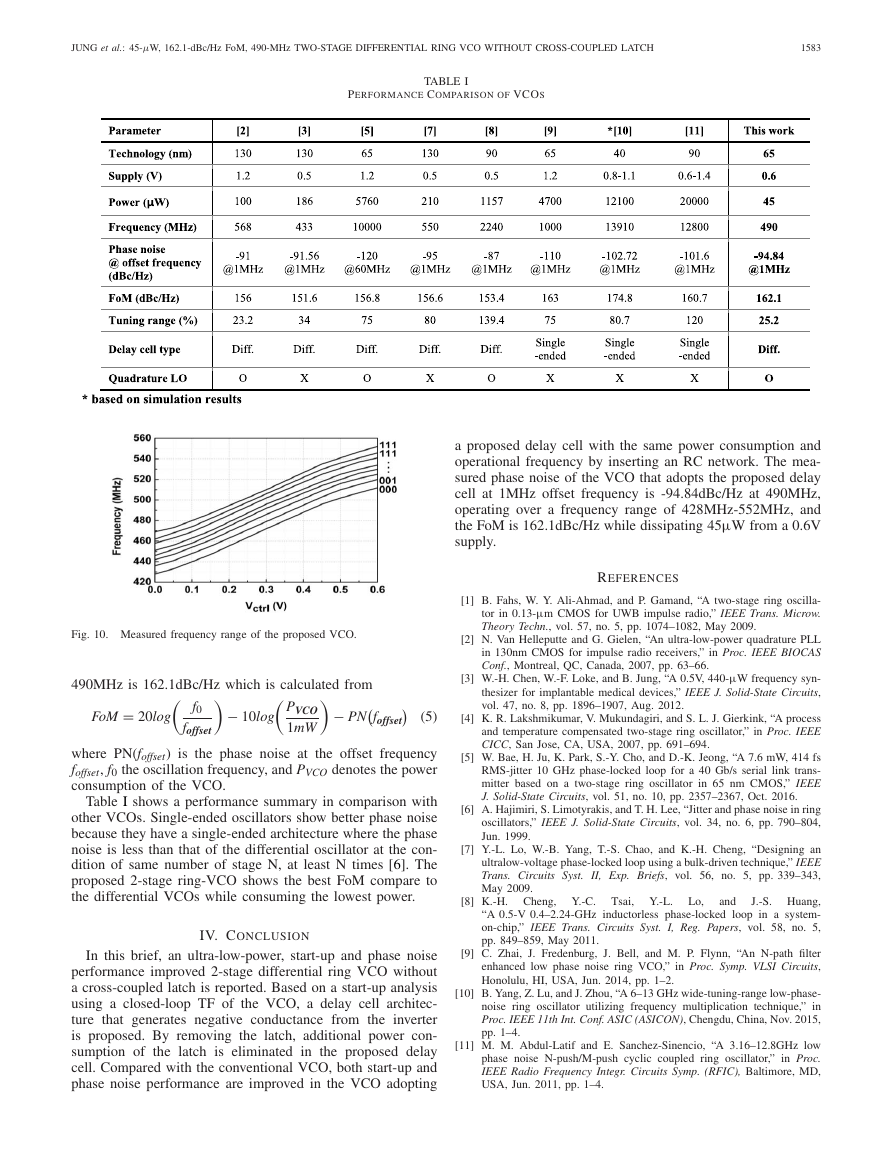
1582 IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS—II: EXPRESS BRIEFS, VOL. 65, NO. 11, NOVEMBER 2018 Fig. 8. Die microphotograph and layout of the proposed VCO as a part of a synthesizer. Fig. 6. Comparison of the normalized ISF and square of rms and dc value. Fig. 7. Comparison of the simulated phase noise (post layout simulation). This delay reduces the turn-on time of MN and MP in the proposed delay cell, making IDN and IDP sharper to realize a narrow current-width. Therefore, Iout becomes similar to an impulse waveform in the proposed delay cell, which leads to lower phase noise in the 1/f2 region while consuming the same power. The comparison of the normalized ISF and square of rms and dc value are shown in Fig. 6. The ISF is calculated by inserting a current pulse at the differential output during a period, and measuring phase change of the output voltage waveform from the original waveform. A comparison of simulated phase noise between the VCOs that adopt the conventional and proposed delay cell is shown in Fig. 7. The VCO with the proposed delay cell, oscillating at 500MHz, shows a 4dB reduction of phase noise at 1MHz while dissipating the same power of 45µW. In Fig. 7, the reduction of the phase noise at frequencies lower than 1MHz is even higher than 4dB. This is ascribed to the following two reasons: (1) In the proposed delay cell, the larger W/L ratio of MN and MP in order to increase Iout,max and the removal of ML reduce 1/f noise generation. (2) Charging (IDP) and dis- charging (IDN) output currents becomes more symmetrical, as shown in Fig. 2(b) and Fig. 3(b), resulting in a more symmet- ric output voltage swing. The symmetry of the output voltage swing suppresses the phase noise in the 1/f3 region due to the smaller dc value of
[6]. Fig. 9. synthesizer adopting the proposed VCO. (a) Measured phase noise and (b) frequency spectrum of the III. MEASUREMENT RESULTS The proposed 2-stage differential ring-VCO is fabricated as a part of a synthesizer unit in a 65nm CMOS pro- cess. Fig. 8 shows the die microphotograph and layout. The additional area for RS and CC can be a drawback in the proposed VCO, however, the area occupied by RS and CC is negligible from a perspective of the VCO used in a fre- quency synthesizer. Fig. 9 shows (a) the measured phase noise and (b) the frequency spectrum of the synthesizer adopting the proposed VCO. The phase noise of the proposed VCO is measured from the out-band phase noise of Fig. 9(a). The phase noise of the proposed VCO at 1MHz frequency off- is −94.84dBc/Hz, while consuming only 45µW from set a 0.6V supply. Fig. 10 shows the measured frequency tun- ing range, which is controlled by the 3-bit digitally-controlled current source and the varactor. The proposed VCO has rel- atively small tuning range due to the current limit, but it can be extended over 60% by controlling the supply from 0.6V to 1V. The figure of merit (FoM) of the proposed VCO at 

JUNG et al.: 45-μW, 162.1-dBc/Hz FoM, 490-MHz TWO-STAGE DIFFERENTIAL RING VCO WITHOUT CROSS-COUPLED LATCH 1583 TABLE I PERFORMANCE COMPARISON OF VCOS a proposed delay cell with the same power consumption and operational frequency by inserting an RC network. The mea- sured phase noise of the VCO that adopts the proposed delay cell at 1MHz offset frequency is -94.84dBc/Hz at 490MHz, operating over a frequency range of 428MHz-552MHz, and the FoM is 162.1dBc/Hz while dissipating 45µW from a 0.6V supply. REFERENCES [1] B. Fahs, W. Y. Ali-Ahmad, and P. Gamand, “A two-stage ring oscilla- tor in 0.13-µm CMOS for UWB impulse radio,” IEEE Trans. Microw. Theory Techn., vol. 57, no. 5, pp. 1074–1082, May 2009. [2] N. Van Helleputte and G. Gielen, “An ultra-low-power quadrature PLL in 130nm CMOS for impulse radio receivers,” in Proc. IEEE BIOCAS Conf., Montreal, QC, Canada, 2007, pp. 63–66. [3] W.-H. Chen, W.-F. Loke, and B. Jung, “A 0.5V, 440-µW frequency syn- thesizer for implantable medical devices,” IEEE J. Solid-State Circuits, vol. 47, no. 8, pp. 1896–1907, Aug. 2012. [4] K. R. Lakshmikumar, V. Mukundagiri, and S. L. J. Gierkink, “A process and temperature compensated two-stage ring oscillator,” in Proc. IEEE CICC, San Jose, CA, USA, 2007, pp. 691–694. [5] W. Bae, H. Ju, K. Park, S.-Y. Cho, and D.-K. Jeong, “A 7.6 mW, 414 fs RMS-jitter 10 GHz phase-locked loop for a 40 Gb/s serial link trans- mitter based on a two-stage ring oscillator in 65 nm CMOS,” IEEE J. Solid-State Circuits, vol. 51, no. 10, pp. 2357–2367, Oct. 2016. [6] A. Hajimiri, S. Limotyrakis, and T. H. Lee, “Jitter and phase noise in ring oscillators,” IEEE J. Solid-State Circuits, vol. 34, no. 6, pp. 790–804, Jun. 1999. [7] Y.-L. Lo, W.-B. Yang, T.-S. Chao, and K.-H. Cheng, “Designing an ultralow-voltage phase-locked loop using a bulk-driven technique,” IEEE Trans. Circuits Syst. II, Exp. Briefs, vol. 56, no. 5, pp. 339–343, May 2009. [8] K.-H. Cheng, Y.-C. J.-S. Huang, “A 0.5-V 0.4–2.24-GHz inductorless phase-locked loop in a system- on-chip,” IEEE Trans. Circuits Syst. I, Reg. Papers, vol. 58, no. 5, pp. 849–859, May 2011. Tsai, Y.-L. and Lo, Fig. 10. Measured frequency range of the proposed VCO. 490MHz is 162.1dBc/Hz which is calculated from − PN foffset FoM = 20log − 10log (5) f0 foffset PVCO 1mW where PN(foffset) is the phase noise at the offset frequency foffset, f0 the oscillation frequency, and PVCO denotes the power consumption of the VCO. Table I shows a performance summary in comparison with other VCOs. Single-ended oscillators show better phase noise because they have a single-ended architecture where the phase noise is less than that of the differential oscillator at the con- dition of same number of stage N, at least N times [6]. The proposed 2-stage ring-VCO shows the best FoM compare to the differential VCOs while consuming the lowest power. IV. CONCLUSION In this brief, an ultra-low-power, start-up and phase noise performance improved 2-stage differential ring VCO without a cross-coupled latch is reported. Based on a start-up analysis using a closed-loop TF of the VCO, a delay cell architec- ture that generates negative conductance from the inverter is proposed. By removing the latch, additional power con- sumption of the latch is eliminated in the proposed delay cell. Compared with the conventional VCO, both start-up and phase noise performance are improved in the VCO adopting [9] C. Zhai, J. Fredenburg, J. Bell, and M. P. Flynn, “An N-path filter enhanced low phase noise ring VCO,” in Proc. Symp. VLSI Circuits, Honolulu, HI, USA, Jun. 2014, pp. 1–2. [10] B. Yang, Z. Lu, and J. Zhou, “A 6–13 GHz wide-tuning-range low-phase- noise ring oscillator utilizing frequency multiplication technique,” in Proc. IEEE 11th Int. Conf. ASIC (ASICON), Chengdu, China, Nov. 2015, pp. 1–4. [11] M. M. Abdul-Latif and E. Sanchez-Sinencio, “A 3.16–12.8GHz low phase noise N-push/M-push cyclic coupled ring oscillator,” in Proc. IEEE Radio Frequency Integr. Circuits Symp. (RFIC), Baltimore, MD, USA, Jun. 2011, pp. 1–4.