2012年贵州省铜仁市中考数学试题及答案.doc-资料库

第1页 / 共11页

第2页 / 共11页

第3页 / 共11页

第4页 / 共11页

第5页 / 共11页

第6页 / 共11页

第7页 / 共11页

第8页 / 共11页

2012 年贵州省铜仁市中考数学试题及答案姓名：准考证号：注意事项 1. 答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置； 2. 答题时，卷 I 必须使用 2B 铅笔，卷 II 必须使用 0.5 毫米黑色签字笔，将答案书写在答题卡规定的位置，字体工整、笔迹清楚； 3. 所有题目必须在答题卡上作答，在试卷上答题无效； 4. 本试卷共 8 页，满分 150 分，考试时间 120 分钟； 5. 考试结束后，将试题卷和答题卡一并收回．卷 I 一、选择题：（本大题共 10 个小题，每小题 4 分，共 40 分）本题每小题均有 A、B、C、D 四个备选答案，其中只有一个是正确的，请你将正确答案的序号填涂在相应的答题卡上． 1．-2 的相反数是（） A. 1 2 B. - 1 2 错误！未找到引用源。 C. -2 D. 2 2．下列四个图形中，既是轴对称图形又是中心对称图形的有（） 2 题图 A．4 个 B．3 个 C．2 个 D．1 个 3．某中学足球队的 18 名队员的年龄情况如下表：年龄（单位：岁）人数 14 3 15 6 16 4 17 4 18 1 则这些队员年龄的众数和中位数分别是（） A．15，15 B．15，15.5 C．15，16 D．16，15 4. 铜仁市对城区主干道进行绿化，计划把某一段公路的一侧全部栽上桂花树，要求路的两端各栽一棵，并且每两棵树的间隔相等．如果每隔 5 米栽 1 棵，则树苗缺 21 棵；如果每隔 6 米栽 1 棵，则树苗正好用完．设原有树苗 x 棵，则根据题意列出方程正确的是（） A. (5 x  21  )1  (6 x  )1 B. (5 x  )21  (6 x  )1 C. (5 x  21  )1  6 x D. (5 x  )21  6 x 5．如图，正方形 ABOC 的边长为 2，反比例函数 y = 的图象经过点 A， k x 5 题图

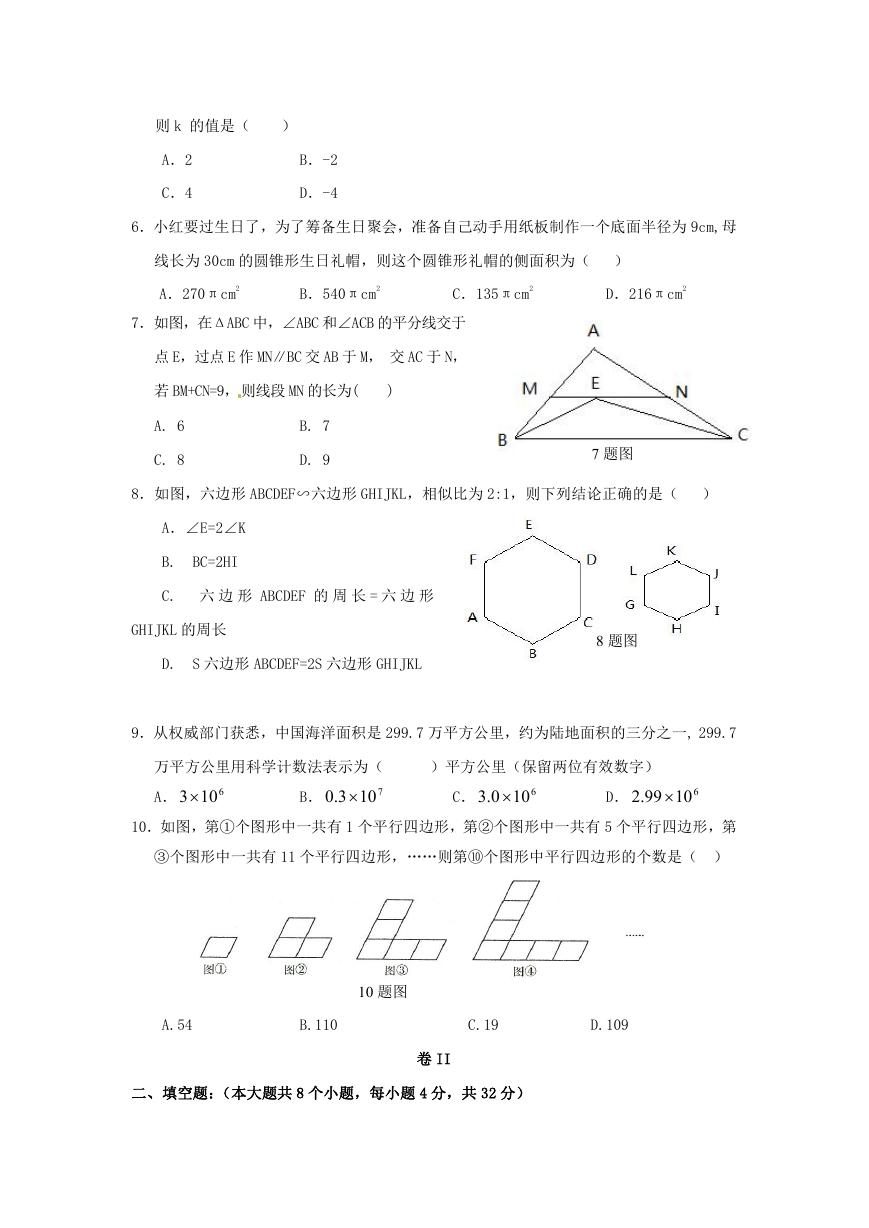
则 k 的值是（）[来源:学科网] A．2 C．4 B．-2 D．-4 6．小红要过生日了，为了筹备生日聚会，准备自己动手用纸板制作一个底面半径为 9cm,母线长为 30cm 的圆锥形生日礼帽，则这个圆锥形礼帽的侧面积为（） A．270πcm2 B．540πcm2 C．135πcm2 D．216πcm2 7．如图，在ΔABC 中，∠ABC 和∠ACB 的平分线交于点 E，过点 E 作 MN∥BC 交 AB 于 M，交 AC 于 N，若 BM+CN=9，则线段 MN 的长为( ) A. 6 C. 8 B. 7 D. 9 7 题图 8．如图，六边形 ABCDEF∽六边形 GHIJKL，相似比为 2:1，则下列结论正确的是（） A．∠E=2∠K B. BC=2HI C. 六边形 ABCDEF 的周长 = 六边形 GHIJKL 的周长 D. S 六边形 ABCDEF=2S 六边形 GHIJKL 8 题图 9．从权威部门获悉，中国海洋面积是 299.7 万平方公里，约为陆地面积的三分之一, 299.7 万平方公里用科学计数法表示为（ 710 3.0  610 3 A． B．）平方公里（保留两位有效数字） 99.2 0.3  610 C． D．  610 10．如图，第①个图形中一共有 1 个平行四边形，第②个图形中一共有 5 个平行四边形，第 ③个图形中一共有 11 个平行四边形，……则第⑩个图形中平行四边形的个数是（） 10 题图 A.54 B.110 C.19 D.109 二、填空题：（本大题共 8 个小题，每小题 4 分，共 32 分）卷 II

11． 2012 - =_________； 12．当 x ___________时，二次根式 1 x 有意义； 13．一个多边形每一个外角都等于 40 ，则这个多边形的边数是______； 14．已知圆 O1 和圆 O2 外切，圆心距为 10cm，圆 O1 的半径为 3cm，则圆 O 2 的半径为 ______； 15．照下图所示的操作步骤，若输入 x 的值为 5，则输出的值为_______________；输入 x 加上 5 平方减去 3 输出 16．一个不透明的口袋中，装有红球 6 个，白球 9 个，黑球 3 个，这些球除颜色不同外没有任何区别，从中任意摸出一个球，则摸到黑球的概率为_______________； 17．一元二次方程 x 22  x  03 的解为__ __________； 18．以边长为 2 的正方形的中心 O 为端点，引两条相互垂直的射线，分别与正方形的边交于 A、B 两点，则线段 AB 的最小值是__________．三、解答题：（本题共 4 个题，19 题每小题 5 分，第 20、21、22 每题 10 分，共 40 分，要有解题的主要过程） 19．（1）化简： 1( x  1  1  1 x )  2 2  x 1 （2）某市计划在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉 M 到广场的两个入口 A、B 的距离相等，且到广场管理处 C 的距离等于 A 和 B 之间距离的一半，A、B、 C 的位置如图所示，请在原图上利用尺规作图作出音乐喷泉 M 的位置，（要求：不写已知、求作、作法和结论，保留作图痕迹，必须用铅笔作图） 19(2)题图

20．如图，E、F 是四边形 ABCD 的对角线 BD 上的两点， AE∥CF，AE=CF，BE=DF. 求证： ΔADE≌ΔCBF． 20 题图 21．某市对参加 2012 年中考的 50000 名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和频数分布直方图的一部分．请根据图表信息回答下列问题：（1）在频数分布表中，a的值为__________，b的值为__________，并将频数分布直方图补充完整；（2）甲同学说“我的视力情况是此次抽样调查所得数据的中位数”，问甲同学的视力情况应在什么范围内？（3）若视力在 4.9 以上（含 4.9）均属正常，则视力正常的人数占被统计人数的百分比是________，并根据上述信息估计全市初中毕业生中视力正常的学生有多少人？频率 21 题图 22．如图，定义：在直角三角形 ABC 中，锐角的邻边与对边的比叫做角的余切，记作 ctan, 即 ctan= 角角   的邻边的对边 AC BC ，根据上述角的余切定义，解下列问题：（1）ctan30◦= ；（2）如图，已知 tanA= 3 ，其中∠A 为锐角，试求 ctanA 4 22 题图

的值．四、（本题满分 12 分） 23．如图，已知⊙O 的直径 AB 与弦 CD 相交于点 E， AB⊥CD，⊙O 的切线 BF 与弦 AD 的延长线相交于点 F．（1）求证：CD∥ BF；（2）若⊙O 的半径为 5， cos∠BCD= 4 5 ，求线段 AD 的长． 23 题图

五、（本题满分 12 分） 24．为了抓住梵净山文化艺术节的商机，某商店决定购进 A、B两种艺术节纪念品．若购进 A种纪念品 8 件，B种纪念品 3 件，需要 950 元；若购进 A种纪念品 5 件，B种纪念品 6 件，需要 800 元．（1）求购进 A、B 两种纪念品每件各需多少元？（2）若该商店决定购进这两种纪念品共 100 件，考虑市场需求和资金周转，用于购买这 100 件纪念品的资金不少于 7500 元，但不超过 7650 元，那么该商店共有几种进货方案？（3）若销售每件 A种纪念品可获利润 20 元，每件 B种纪念品可获利润 30 元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少元？六、（本题满分 14 分） 25．如图已知：直线 y 3 x 交 x 轴于点 A，交 y 轴于点 B，抛物线 y=ax2+bx+c 经过 A、 B、C（1，0）三点. （1）求抛物线的解析式; （2）若点 D 的坐标为（-1，0），在直线 y 3 x 上有一点 P,使ΔABO 与ΔADP 相似，求出点 P 的坐标；（3）在（2）的条件下，在 x 轴下方的抛物线上，是否存在点 E，使ΔADE 的面积等于四边形 APCE 的面积？如果存在，请求出点 E 的坐标；如果不存在，请说明理由． 25 题图

数学参考答案及评分标准一、选择题(每小题 4 分)：题号答案 1 D 2 B 3 B 4 A 5 D 6 A 7 D 8 B 9 C 10 D 二、填空题（每小题 4 分）: 11、2012； 12、 0> ； 13、9； 14、7cm； 15、97； 16、三、解答题[来源:学科网] 1 6 ； 17、3 1或 - ； 18、 2 . 19.（1）（5 分）解：原式= 1( x  1  1  x )  1 1 x 2  2 ………………………………1 分[来源:学科网 ZXXK] x = 1 x  2  1 x 1  x 12  2 …………………. ……………….……3 分 = -1……………………………………………………… ………5 分（2）（5 分）作图：连结 AB………………………………………………………1 分作出线段 AB 的垂直平分线……………………………………………3 分在矩形中标出点 M 的位置…………………………………………… 5 分 [来源:学科网] （必须保留尺规作图的痕迹，痕迹不全少一处扣 1 分，不用直尺连结 AB 不给分，无圆规痕迹不给分．） 20.（10 分）证明：∵AE∥CF ∴∠AED=∠CFB…………………… 3 分 ∵DF=BE ∴DF+EF=BE+EF 即 DE=BF………6 分在△ADE 和△CBF 中  AED  CF  BF AE      DE  ∴△ADE≌△CBF（SAS）……… 10 分 CFB …………………９分

21.（10 分）解：（1）60；0.05；补全图形……………….. 3 分（2）4.6  x<4.9 ……………………….…. 6 分（3）35%……………………………………7 分 50000  %35  17500 (人)………… 10 分 22.（10 分）解：(1) 3 ……………………. 5 分（2） A tan  ∴ c tan  BC AC AC BC   3 4 4 3 , ……………. . 10 分四、23.（12 分）（1）证明：∵BF 是圆 O 的切线，AB 是圆 O 的直径 ∴BF⊥AB…………………………………………3 分 ∵CD⊥AB ∴CD∥BF ………………………………….…… 6 分（2）解：∵AB 是圆 O 的直径 ∴∠ADB=90º ………………………………… 7 分 ∵圆 O 的半径 5 ∴AB=10 ……………………………………… 8 分 ∵∠BAD=∠BCD …………………………… 10 分 ∴ cos∠BAD= cos∠BCD= ∴ AD  cos  BAD  AB = 4 AD 5 AB 10  4 5 =8 ∴AD=8…………………………………………12 分五、24.（12 分）解：（1）设该商店购进一件 A种纪念品需要 a元，购进一件 B种纪念品需要 b 元, 根据题意得方程组 8 a   5 a    3 b 6 b   950 800 …………………………………………………………2 分

资料库

2012年贵州省铜仁市中考数学试题及答案.doc

相关推荐

中考

热门标签

最新资料