MATLAB软件介绍.pdf-资料库

qq_26873731-10403851-4744302543344265214.pdf-第1页.png

第1页 / 共172页

qq_26873731-10403851-4744302543344265214.pdf-第2页.png

第2页 / 共172页

qq_26873731-10403851-4744302543344265214.pdf-第3页.png

第3页 / 共172页

qq_26873731-10403851-4744302543344265214.pdf-第4页.png

第4页 / 共172页

qq_26873731-10403851-4744302543344265214.pdf-第5页.png

第5页 / 共172页

qq_26873731-10403851-4744302543344265214.pdf-第6页.png

第6页 / 共172页

qq_26873731-10403851-4744302543344265214.pdf-第7页.png

第7页 / 共172页

qq_26873731-10403851-4744302543344265214.pdf-第8页.png

第8页 / 共172页

Matlab 软件目录 1、Matlab 帮助的使用 ........................................................................ 3 2、Matlab 数据输入与类型 ................................................................ 4 3、Matlab 数据处理 .......................................................................... 15 4、Matlab 编程 .................................................................................. 26 5、Matlab 绘图命令 .......................................................................... 33 6、Matlab 在数值模拟中的几个应用 .............................................. 59 7、Matlab 在高等数学中的应用 ...................................................... 76 8、Matlab 在线性代数中的应用 .................................................... 101 9、Matlab 图论工具箱 .................................................................... 109 10、评价方法 .................................................................................. 115 11、预测方法 .................................................................................. 130 12、智能算法 .................................................................................. 143 13、Simulink 初步 .......................................................................... 150 14、Matlab 在概率统计中的应用 .................................................. 163 15、分形 .......................................................................................... 167 参考文献 .......................................................................................... 172 1

作为和 Mathematica、Maple 并列的三大数学软件。其强项就是其强大的矩阵计算以及仿真能力。要知道 Matlab 的由来就是 Matrix + Laboratory = Matlab，所以这个软件在国内也被称作《矩阵实验室》。每次 MathWorks 发布 Matlab 的同时也会发布仿真工具 Simulink。在欧美很多大公司在将产品投入实际使用之前都会进行仿真试验，他们所主要使用的仿真软件就是 Simulink。Matlab 提供了自己的编译器：全面兼容 C++以及 Fortran 两大语言。所以 Matlab 是工程师，科研工作者手上最好的语言，最好的工具和环境。 Matlab 已经成为广大科研人员的最值得信赖的助手和朋友！目前 MATLAB 产品族可以用来进行：－数值分析－数值和符号计算－工程与科学绘图－控制系统的设计与方针－数字图像处理－数字信号处理－通讯系统设计与仿真－财务与金融工程... Simulink 是基于 MATLAB 的框图设计环境，可以用来对各种动态系统进行建模、分析和仿真，它的建模范围广泛，可以针对任何能够用数学来描述的系统进行建模，例如航空航天动力学系统、卫星控制制导系统、通讯系统、船舶及汽车等等，其中了包括连续、离散，条件执行，事件驱动，单速率、多速率和混杂系统等等。 Simulink 提供了利用鼠标拖放的方法建立系统框图模型的图形界面，而且 Simulink 还提供了丰富的功能块以及不同的专业模块集合，利用 Simulink 几乎可以做到不书写一行代码完成整个动态系统的建模工作。 2

1、Matlab 帮助的使用 1.1 help help%帮助总览 help elfun %关于基本函数的帮助信息 help exp %指数函数 exp 的详细信息 1.2 lookfor 指令当要查找具有某种功能但又不知道准确名字的指令时，help 的能力就不够了，lookfor 可以根据用户提供的完整或不完整的关键词，去搜索出一组与之相关的指令。 lookfor integral %查找有关积分的指令 lookfor fourier %查找能进行傅里叶变换的指令 1.3 超文本格式的帮助文件在 Matlab 中，关于一个函数的帮助信息可以用 doc 命令以超文本的方式给出，如 doc  doc doc  doc eig %eig 求矩阵的特征值和特征向量 1.4 pdf 帮助文件可从 MathWorks 网站上下载有关的 pdf 帮助文件。网站地址：http://www.mathworks.com/ 3

2、Matlab 数据输入与类型 2.1 Matlab 中的变量 MATLAB 程序中的基本数据单元称为阵列(Array)，是一个分为行与列的数据集合。变量被看作是只有一行一列的阵列。MATLAB 语言不需要对变量进行事先声明，也不需要指定变量类型，它会自动根据所赋予变量的值或对变量所进行的操作来确定变量的类型。其命名规则为：（1）变量名的大小写是敏感的。（2）变量的第一个字符必须为英文字母，而且不能超过 31 个字符。（3）变量名可以包含下划线、数字，但不能为空格符、标点。（4）命名变量时可以取一个容易记忆并且能表达出其含义的名称，如汇率，可以定义为 exchange_rate。对于变量作用域，默认情况是局部变量，使用 global 定义全局变量，而且全局变量常用大写的英文字母表示。 MATLAB 预定义的变量如下表所示： ans eps pi inf NaN i 或 j nargin nargout realmax realmin flops 预设的计算结果的变量名 MATLAB 定义的正的极小值=2.2204e-16 内建的π值 ∞值，无限大无法定义一个数目虚数单位 i=j=√-1 函数输入参数个数函数输出参数个数最大的正实数 2 1023 最小的正实数 2 -1022 浮点运算次数 4

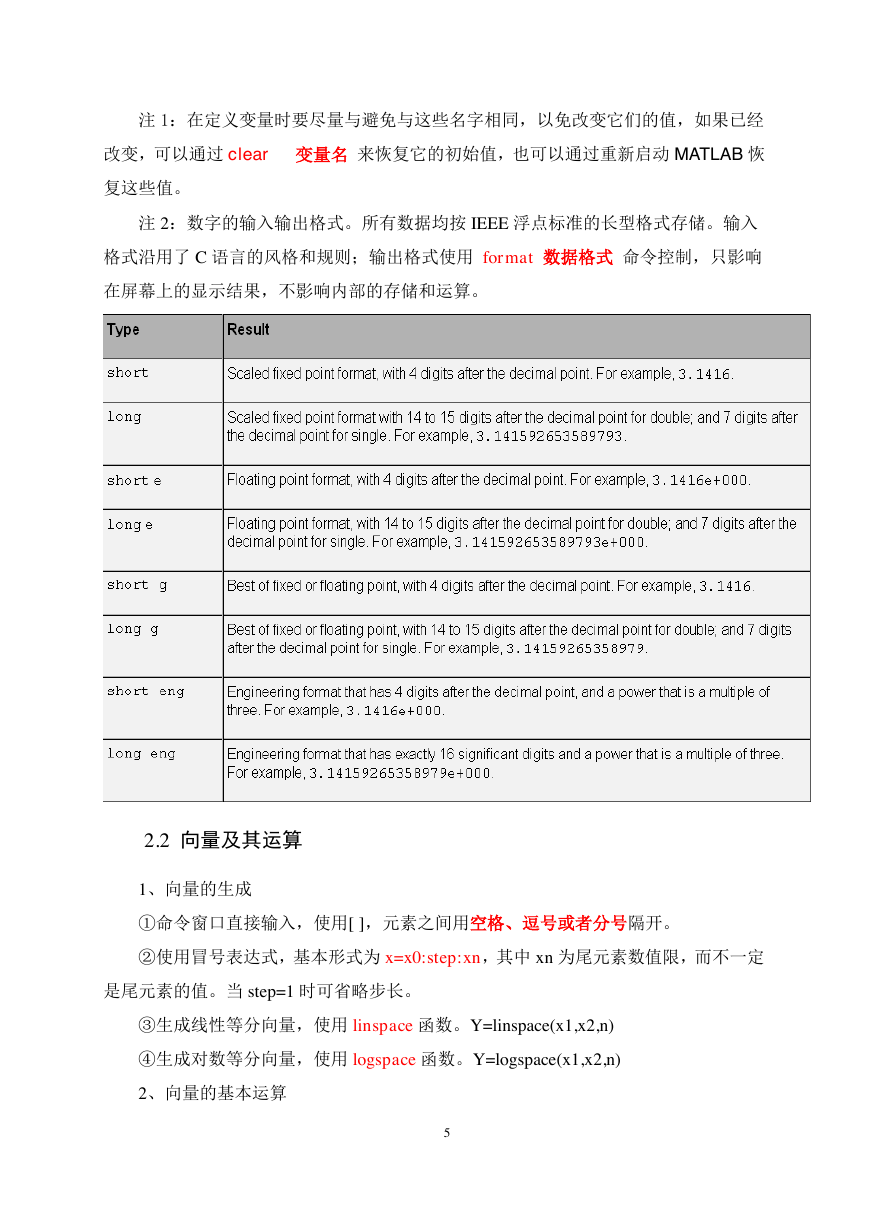
注 1：在定义变量时要尽量与避免与这些名字相同，以免改变它们的值，如果已经改变，可以通过 clear 变量名来恢复它的初始值，也可以通过重新启动 MATLAB 恢复这些值。注 2：数字的输入输出格式。所有数据均按 IEEE 浮点标准的长型格式存储。输入格式沿用了 C 语言的风格和规则；输出格式使用 format 数据格式命令控制，只影响在屏幕上的显示结果，不影响内部的存储和运算。 2.2 向量及其运算 1、向量的生成 ①命令窗口直接输入，使用[ ]，元素之间用空格、逗号或者分号隔开。 ②使用冒号表达式，基本形式为 x=x0:step:xn，其中 xn 为尾元素数值限，而不一定是尾元素的值。当 step=1 时可省略步长。 ③生成线性等分向量，使用 linspace 函数。Y=linspace(x1,x2,n) ④生成对数等分向量，使用 logspace 函数。Y=logspace(x1,x2,n) 2、向量的基本运算 5

数加（减）、数乘、点积(dot 函数)、叉积(cross 函数)、混合积 dot(a,cross(b,c)) 示例：（1）dot（a，b）返回向量 a 和 b 的数量点积。a 和 b 必须同维。当 a 和 b 都为列向量时，dot（a，b）同于 a.*b。 dot（a，b，dim）返回 a 和 b 在维数为 dim 的点积。dim=1 按列点积，dim=2 对应按行点积，dim>=3 时逐个元素点积。 A=[1 2 3;4 5 6;7 8 9]; B=[7 8 9;1 2 3;4 5 6]; dot(A,B,1)，dot(A,B,2)，dot(A,B,3) （2）c = cross（a，b，dim）当 a 和 b 为 n 维数组时，则返回 a 和 b 的 dim 维向量的叉积。a 和 b 必须有相同的维数。且 size（a，dim）和 size（a，dim）必须为 3。dim 的含义和 dot 中的 dim 一样。 A=[1 2 3;4 5 6;7 8 9]; B=[7 8 9;1 2 3;4 5 6]; cross(A,B,1)，cross(A,B,2) 2.3 矩阵及其运算 1、简单矩阵的输入（1）要直接输入矩阵时，矩阵一行中的元素用空格或逗号分隔；矩阵行与行之间用分号“;”隔离，整个矩阵放在方括号“[ ]”里。 A=[1,2,3;4,5,6;7,8,9]  说明：指令执行后，矩阵 A 被保存在 Matlab 的工作空间中，以备后用。如果用户不用 clear 指令清除它，或对它进行重新赋值，那么该矩阵会一直保存在工作空间中，直到本次指令窗关闭为止。（2）矩阵的分行输入，此时回车键作为分行标志， A=[1,2,3 4,5,6 7,8,9] （3）使用 M 文件创建大矩阵，当矩阵维数非常大时，可以创建 m 文件，在 m 文件中输入数据或者导出数据文件。 6

2、矩阵的基本运算 ①矩阵的四则运算。其中乘法运算要注意相乘的双方有相邻公共维，除法分为左除 “\” (A\B=inv(A)*B)和右除”/”（ A/B=A*inv (B)）(需要计算逆矩阵) ②矩阵的逆运算。inv 函数。 ③矩阵的幂运算。^。 ④矩阵的指数运算。exp(返回每个元素的指数值)，expm([V,D] = EIG(X) ， expm(X) = V*diag(exp(diag(D)))/V)，expm1(exp(x)-1) ⑤矩阵的对数运算。logm，A=logm(B)/log(10)，B=10^A ⑥矩阵的特征值函数。eig 和 eigs(适合于大型稀疏方阵) ⑦矩阵的奇异值函数。svd（[U,S,V] = SVD(X)，X = U*S*V'）和 svds ⑧矩阵的条件数函数。cond（矩阵 A 的条件数等于 A 的范数与 A 的逆的范数的乘积，c = cond(A,p)等价于 norm(A,p) * norm(inv(A),p)），condest(1 范数的条件数的估计值)， rcond ⑨特征值的条件数函数。codeig（[V,D,s] = condeig(A) 等价于[V,D] = eig(A); s =condeig(A);） ⑩范数函数。norm（1-范数：即列范数，矩阵的各列绝对值之和的最大值；2-范数：所有元素的平方和开根号(默认)；无穷范数：即行范数，矩阵各行的绝对值之和的最大值）， normest (矩阵的 2 范数的估计值) 其他还有秩函数 rank，迹函数 trace，零空间函数 null（又称为核空间， X=null(A)，则 A*X=0，X‟*X=I），正交空间函数 orth(B = orth(A),则 B'*B = eye(rank(A)))，伪逆函数 pinv 等。 3、特殊向量和特殊矩阵（1）特殊向量 t=[0:0.1:10] %产生从 0 到 10 的行向量，元素之间间隔为 0.1 t=linspace(n1,n2,n) %产生 n1 和 n2 之间线性均匀分布的 n 个数 (缺省 n 时,产生 100 个数) t=logspace(n1,n2,n) (缺省 n 时,产生 50 个数) %在和之间按照对数距离等间距产生 n 个数。（2）特殊矩阵 i)单位矩阵 7

eye(m), eye(m,n) 可得到一个可允许的最大单位矩阵而其余处补 0, eye(size(a)) 可以得到与矩阵 a 同样大小的单位矩阵。 ii)所有元素为 1 的矩阵 ones(n)，ones(size(a))，ones(m，n)。 iii）所有元素为 0 的矩阵 zeros(n)，zeros(m,n)。 iv）空矩阵是一个特殊矩阵，这在线性代数中是不存在的。例如 q=[ ] 矩阵 q 在工作空间之中，但它的大小为零。通过空矩阵的办法可以删除矩阵的行与列。例如 a(:,3)=[] 表示删除矩阵 a 的第 3 列。 v）随机数矩阵 rand(m,n) 产生 m×n 矩阵，其中的元素是服从[0,1]上均匀分布的随机数。 randint(m,n,[min,max]) 产生 m×n 矩阵，其中的元素是[min,max]上的随机整数。 normrnd(mu,sigma,m,n)产生 m×n 矩阵，其中的元素是服从均值为 mu，标准差为 sigma 的正态分布的随机数。 exprnd(mu,m,n) 产生 m×n 矩阵，其中的元素是服从均值为 mu 的指数分布的随机数。 poissrnd(mu,m,n) 产生 m×n 矩阵，其中的元素是服从均值为 mu 的泊松（Poisson）分布的随机数。 unifrnd(a,b,m,n) 产生 m×n 矩阵，其中的元素是服从区间[a,b]上均匀分布的随机数。 r = mvnrnd(MU,SIGMA,cases) 产生 cases 对均值向量为 MU，协方差阵为 SIGMA 的多维正态分布的随机数。 vi）随机置换 randperm(n)产生 1 到 n 的一个随机全排列。 perms([1:n])产生 1 到 n 的所有全排列。 vii)稀疏矩阵稀疏矩阵是指矩阵中零元素很多，非零元素很少的矩阵。对于稀疏矩阵，只要存放 8

资料库

MATLAB软件介绍.pdf

相关推荐

课程资源

热门标签

最新资料