logo资料库

计量经济学 第四版 庞皓 第四章练习题及参考解答（第四版）.docx

发布时间：2022-06-02 发布人：admin 分类：说明书 资料大小：5.04M 资料格式：docx 举报 版权申诉
第1页 / 共13页
第2页 / 共13页
第3页 / 共13页
第4页 / 共13页
第5页 / 共13页
第6页 / 共13页
第7页 / 共13页
第8页 / 共13页
资料共13页，剩余部分请下载后查看
    第四章练习题及参考解答 4.1 假设在模型 Y i   2  1 X 2 i   3 X 3 i  u i 中， X 与 之间的相关系数为零，有 2 X 3 人建议你分别进行如下回归： Y i Y i 1   X  u 1 i 2 i   2 X ˆ   1 3 ˆ ˆ  3  且    u ˆ 3 i 3 2 2 2 i (1) 是否存在 ？为什么？ 1 ˆ 会等于 1ˆ 或 1ˆ 或者两者的某个线性组合吗？  ˆ Var  3 (2) (3) 是否有  Var 且  Var ˆ Var  2 ˆ  2 ˆ  3       ？ ˆ ˆ     (1) 存在 2 3 【练习题 4.1 参考解答】 ˆ 且 3   ˆ 2  2 因为 ˆ  2  i 2 3 i   y x x  i     2 x 3 i  x 2 2 i   y x i     。  3 i x x 2 i 2   3 i  x x 2 i  3 i X 当 2 X与 之间的相关系数为零时，离差形式的 3 x x  2 3 i i 0 有 同理有： (2)会的。 (3) 存在 因为 ˆ  2 i 2      x y x i     2 2 x x 3 2 i i ˆ ˆ  3 3    y x i  2 x 2 i 2 i  ˆ  2 2 3 i  var  ˆ  2  且 var  ˆ  3   var  ˆ  3  var var    ˆ  2   ˆ   2    2   2 1ix 2  2 r 23   x 2   2 1 2 i   ˆ  3 当 23 r  时， 0 var  ˆ  2 同理，有 var  ˆ  3   var   2 r 23  2   x 2 2 i  var  ˆ  2  4.2 表4.4给出了1995—2016年中国商品进口额Y、国内生产总值GDP、居民消费价格 指数CPI的数据。 表4.4 中国商品进口额、国内生产总值、居民消费价格指数 1
    年 份 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 商品进口额 (亿元)Y 11048.1 11557.4 11806.5 11626.1 13736.4 18638.8 20159.2 24430.3 34195.6 46435.8 54273.7 63376.9 73284.6 79526.5 68618.4 94699.3 113161.4 114801.0 121037.5 120358.0 104336.1 104967.2 国内生产总值 (亿元)GDP 61339.9 71813.6 79715.0 85195.5 90564.4 100280.1 110863.1 121717.4 137422.0 161840.2 187318.9 219438.5 270232.3 319515.5 349081.4 413030.3 489300.6 540367.4 595244.4 643 974.0 689 052.1 744 127.2 居民消费价格指数 (1978=100)CPI 396.9 429.9 441.9 438.4 432.2 434.0 437.0 433.5 438.7 455.8 464.0 471.0 493.6 522.7 519.0 536.1 565.0 579.7 594.8 606.7 615.2 627.5 资料来源：《中国统计年鉴 2017》  考虑建立模型： ln Y t ＋ 1 2 ln GDP t   3 ln CPI t  u i (1)利用表中数据估计此模型的参数。 (2)你认为数据中有多重共线性吗？ ln (3)进行以下回归： ln  Y t A A GDP v  ＋ 1 1 i 2 t ln ln  ln Y t GDP C C B B ＋ 2 1   CPI ln 1 2 t  v 2 t CPI t i  v 3 i 根据这些回归你能对多重共线性的性质有什么认识? (4)假设经检验数据有多重共线性，但模型中 著，你对此模型的应用有何建议? 【练习题 4.2 参考解答】 ˆ  和 在5%水平上显著，并且F检验也显 2 ˆ 3 建立模型： ln Y t  ＋ 2 1 ln GDP t   3 ln CPI t  u i (1)利用表中数据估计此模型的参数。 2
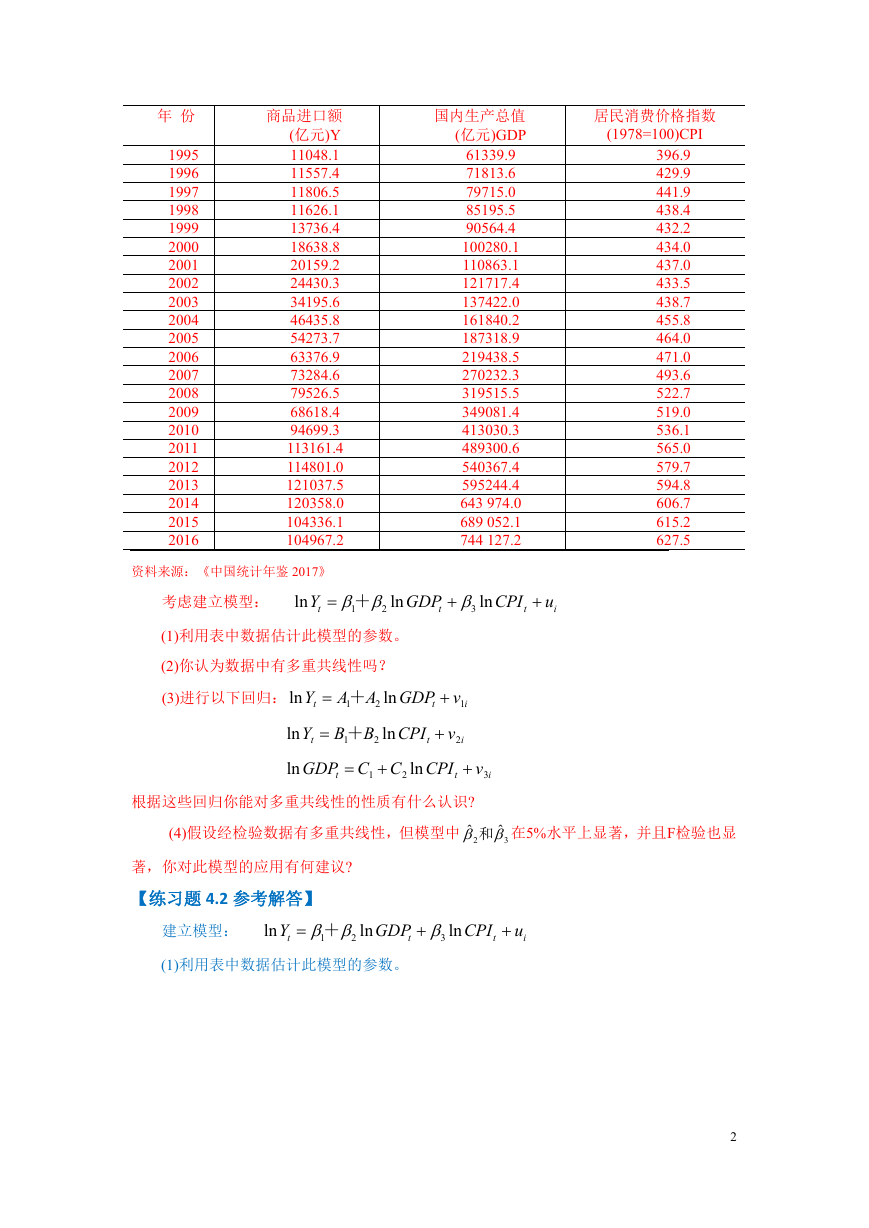
    (2)你认为数据中有多重共线性吗？ 其中居民消费价格指数 CPI 对商品进口额影响为负，与预期不符合，可能存在多重共线性。 (3)分别进行以下回归： 1）作回归 ln Y t  A A GDP v  ＋ 1 1 i ln 2 t 说明 GDP 的确对商品进口额有正的影响，是重要变量。 2)作回归 ln Y t  B B ＋ 1 2 ln CPI t  v 2 i 说明 CPI 的确对商品进口额有正的影响，是重要变量。 3)作回归 ln GDP C C   t 1 ln CPI t 2  v 3 i 3
    说明 CPI 与 GDP 也高度相关，这是引起多重共线性的原因所在。 4.3 在本章开始的“引子”提出的“工业增加值增长会减少财政收入吗？”的例子中， 如果所采用的数据如表4.5所示，试分析：为什么会出现本章开始时所得出的异常结果？你 怎样解决所出现的问题？ 表4.5 2000-2016年财政收入及其影响因素数据 （ 单位：亿元） 一般公共预算收入 国内生产总值 税收总额 工业增加值 年 份 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 CZSR 13395.23 16386.04 18903.64 21715.25 26396.47 31649.29 38760.20 51321.78 61330.35 68518.30 83101.51 103874.43 117253.00 129209.64 140370.03 152269.23 159604.97 资料来源：《中国统计年鉴2017》 【练习题 4.3 参考解答】 GDP 100280.1 110863.1 121717.4 137422.0 161840.2 187318.9 219438.5 270232.3 319515.5 349081.4 413030.3 489300.6 540367.4 595244.4 643974.0 689052.1 744127.2 SSZE 12581.51 15301.38 17636.45 20017.31 24165.68 28778.54 34804.35 45621.97 54223.79 59521.59 73210.79 89738.39 100614.28 110530.70 119175.31 124922.20 130360.73 GYZJZ 40259.7 43855.6 47776.6 55363.8 65776.8 77960.5 92238.4 111693.9 131727.6 138095.5 165126.4 195142.8 208905.6 222337.6 233856.4 236506.3 247860.1 4
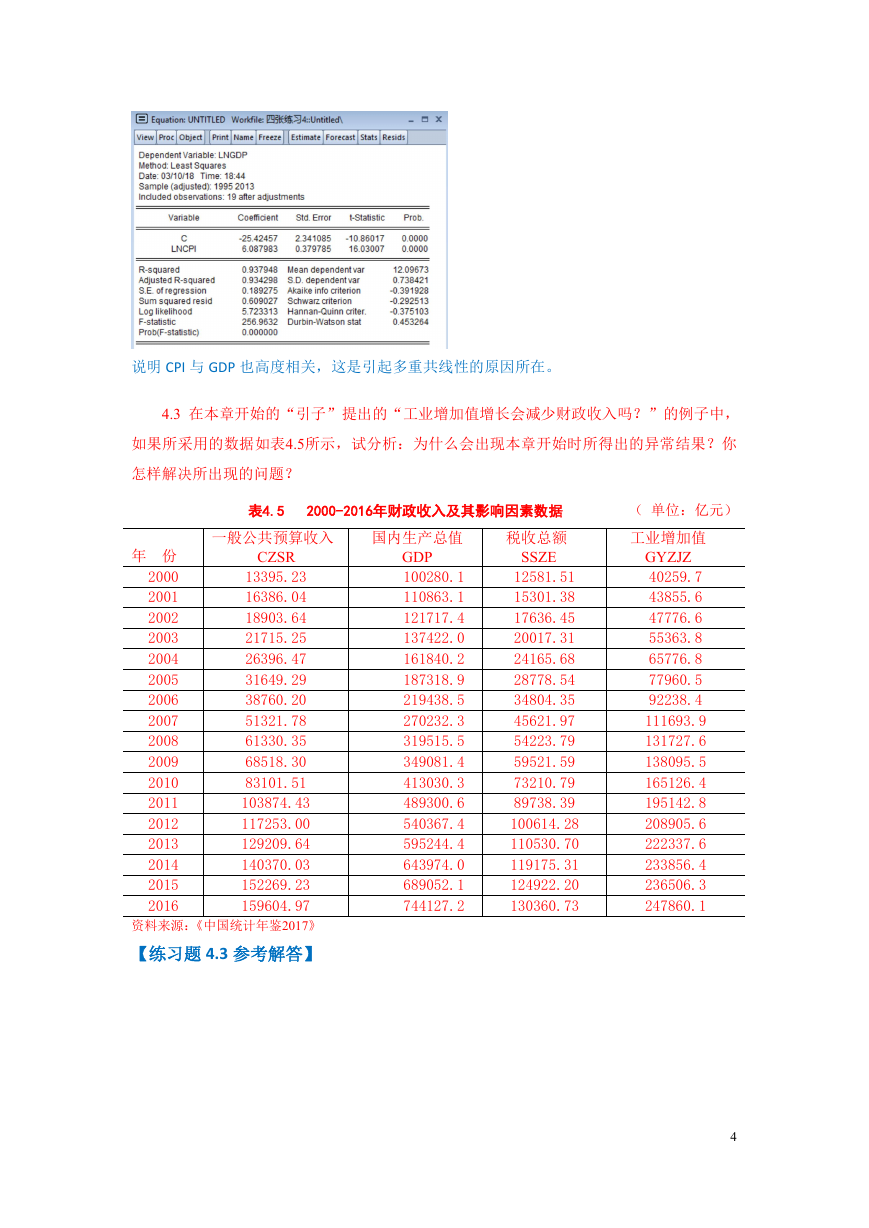
    计算解释变量的相关系数： 解释变量的方差扩大因子 VIF ： 这说明由于严重的多重共线性导致工业增加值的参数为负。 工业增加值与国内生产总值、税收总额都高度相关，为分析工业增加值对一般公共预 算收入是否有负的影响，可删除国内生产总值、税收总额作回归： 5
    这说工业增加值对一般公共预算收入是有证的租金作用的。不过国内生产总值、税收 总额都是对一般公共预算收入有重要影响的变量，删除后可能模型会有设定误差。 4.4 表4.6是中国家电零售总额及国内生产总值、人均可支配收入、家电广告投放总额、 居民消费价格指数等数据。 表4.6 家 电 零 售 总 额 tY （亿元） 年份 GDP 元） 1997年—2015年中国家电零售总额及相关数据 2X （ 亿 人均可支配收 入 3X （元） 家电广告投放 总 额 4X （ 亿 元） 居 民 消 费 价 格 指 数 5X （以1996年 为100） 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 数据来源:国家统计局(www.stats.gov.cn)。 78802.9 83817.6 89366.5 99066.1 109276.2 120480.4 136576.3 161415.4 185998.9 219028.5 270844 321500.5 348498.5 411265.2 484753.2 539116.5 590422.4 644791.1 682635.1 506.0 651.7 724.3 831.6 784.7 953.0 1127.2 1415.7 1636.0 1921.7 2370.7 2706.6 3154.4 4056.5 5374.9 5935.8 6944.5 7603.3 8269.5 5160.3 5425.1 5854.0 6280.0 6859.6 7702.8 8472.2 9421.6 10493.0 11759.5 13785.8 15780.8 17174.7 19109.4 21809.8 24564.7 26955.1 29381.0 31790.3 64.71 79.02 67.14 73.51 65.88 78.74 88.00 76.51 77.4 88.61 94.40 87.92 98.67 119.43 140.34 205.09 229.73 246.83 277.19 102.8 102.0 100.5 101.0 101.7 100.8 102.1 106.0 107.9 109.6 114.8 121.6 120.7 124.7 131.5 134.9 138.4 141.2 143.1 （1）如果请考虑建立模型： Y t    ＋ 1 2 X 2 t   3 X 3 t   4 X 4 t +  5 X 5 t  u i ，利用表中数据估 计此模型的参数。 (2)根据模型估计结果，你认为参数估计结果合理吗？数据中有吗？ (3)分别采用简单相关系数检验法和方差扩大因子法验证模型是否存在多重共线性。 6
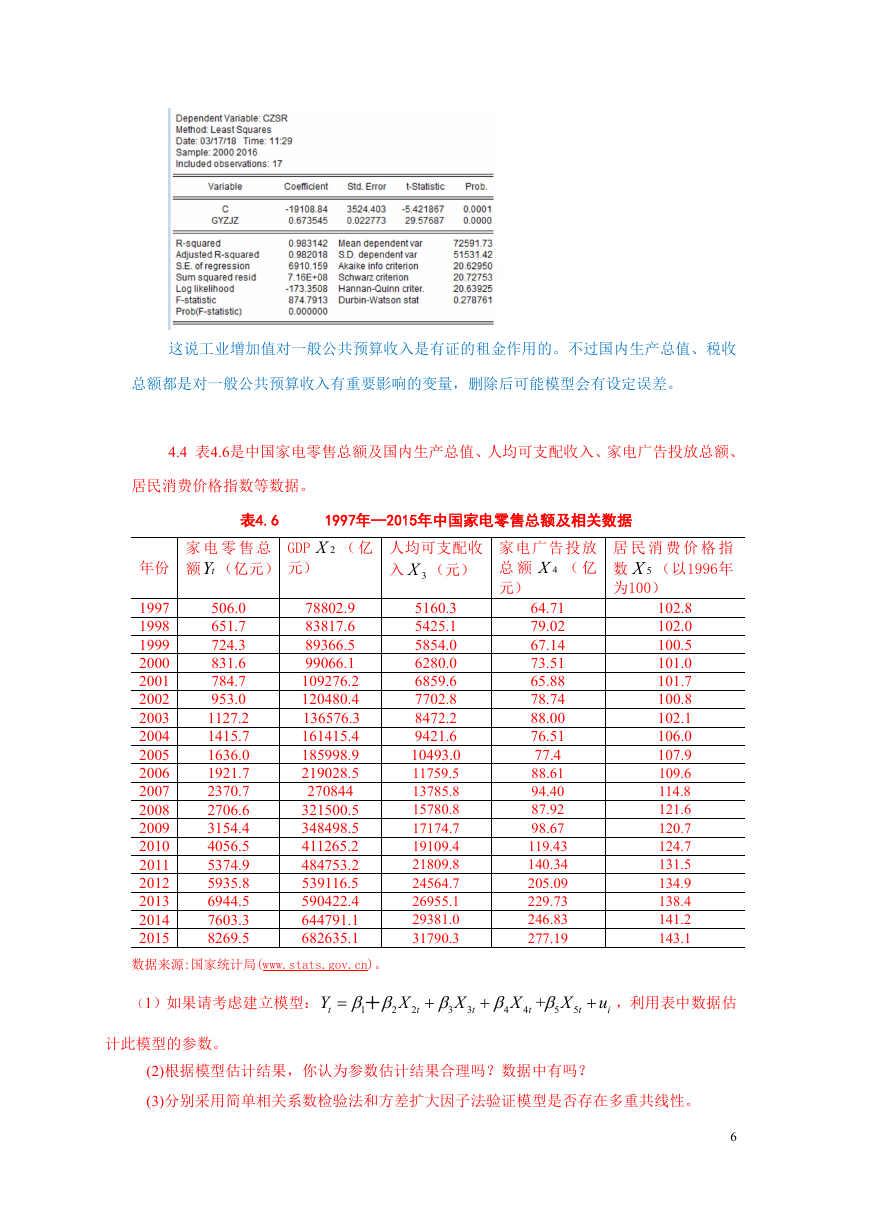
    （4）如果存在多重共线性，如何才能解决？ 【练习题 4.4 参考解答】 OLS方法估计模型参数，得到的回归结果。 该模型 2 R  0.9977, R 2  0.9970 ，可决系数很高，F检验值1501.140，明显显著。但是当  0.05 时 t  /2 ( n k  )  t 0.025 (19 5)   2.145 ，不仅X3、X5的系数不显著，而且X3的符号与预 期相反，这表明可能存在严重的多重共线性。 计算各解释变量的相关系数。 变量 X2 X3 X4 X5 X2 1.000000 0.998932 0.937585 0.995145 X3 0.998932 1.000000 0.941257 0.991385 X4 0.937585 0.941257 1.000000 0.917290 X5 0.995145 0.991385 0.917290 1.000000 由相关系数矩阵可以看出，所有解释变量之间的相关系数较高，证实确实存在一定的多 重共线性。 解释变量的方差扩大因子 VIF 被解释变量 方差扩大因子 X2 X3 X4 X5 1335.613 723.4567 10.4945 185.1135 所有解释变量的方差扩大因子都远大于 10，表明存在严重多重共线性问题。 对多重共线性的处理： 将各变量进行对数变换（ 5X 除外），再对以下模型进行估计。 7
    ln Y t    1 2  ln X 2 t   3 ln X 3 t   4 ln X 4 t   5 X 5 t  u t 该模型 2 R  0.9974, R 2  0.9967 ，可决系数很高，F检验值1366.756，明显显著。但是取  0.05 时 t  /2 ( n k  )  t 0.025 (19 5)   2.145 ，LNX3和LNX5依然不显著，且LNX3的回归系数 符号与预期不相符，这表明经对数变换后的模型依然存在严重的多重共线性，需要更进一步的 修正方法。 采用逐步回归方法筛选并剔除引起多重共线性的变量，最后保留的解释变量为 2X 和 4X ， 估计结果为 ˆ Y   958.3489 0.0090 2 10.9547 4 X X   (75.0751) (0.0005) (1.5102) t=（-12.7652） (18.2819) (7.2538) 2 R  0.9970 2 R  0.9966 F=2627.512 该模型中 2 R  0.9970, R 2  0.9966 ，可决系数很高，F检验值2627.512，明显显著。 当  0.05 时 t  /2 ( n k  )  t 0.025 (19 5)   2.145 ，所有系数估计值高度显著。对系数估计值 的解释如下：在其他变量保持不变的情况下，如果国内生产总值GDP每增加一亿元，则家电 零售总额将增加90万元；家电广告投放总额每增加一亿元，则家电零售总额将增加10.9547 亿元。 4.5表4.7中给出了四川省城镇人均消费支出Y和其相关影响因素城镇居民人均可支配收 入X2、地区生产总值X3、零售商品价格指数X4以及人口自然增长率X5的数据。 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料