logo资料库

2021-2022学年福建省龙岩市长汀县八年级下学期期中数学试题及答案.doc

发布时间：2023-11-09 发布人：admin 分类：说明书 资料大小：0.74M 资料格式：doc 举报 版权申诉
第1页 / 共12页
第2页 / 共12页
第3页 / 共12页
第4页 / 共12页
第5页 / 共12页
第6页 / 共12页
第7页 / 共12页
第8页 / 共12页
资料共12页，剩余部分请下载后查看
    2021-2022 学年福建省龙岩市长汀县八年级下学期期中数学试题及答 案 (考试时间：120 分钟满分 150 分) 一、选择题(每小题 4 分，共 40 分) 1.若 3 x 在实数范围内有意义，则 x的取值范是 A. 3x  C. 3x  B. 3x  D. 2.下列各式中计算正确的是 A.    B. 3 1  29 3 x   9    C. 25 1 5  D.  2 2   2 3.计算： 18  □ ，则□中的数是 3 A.6B. 6 C.2D. 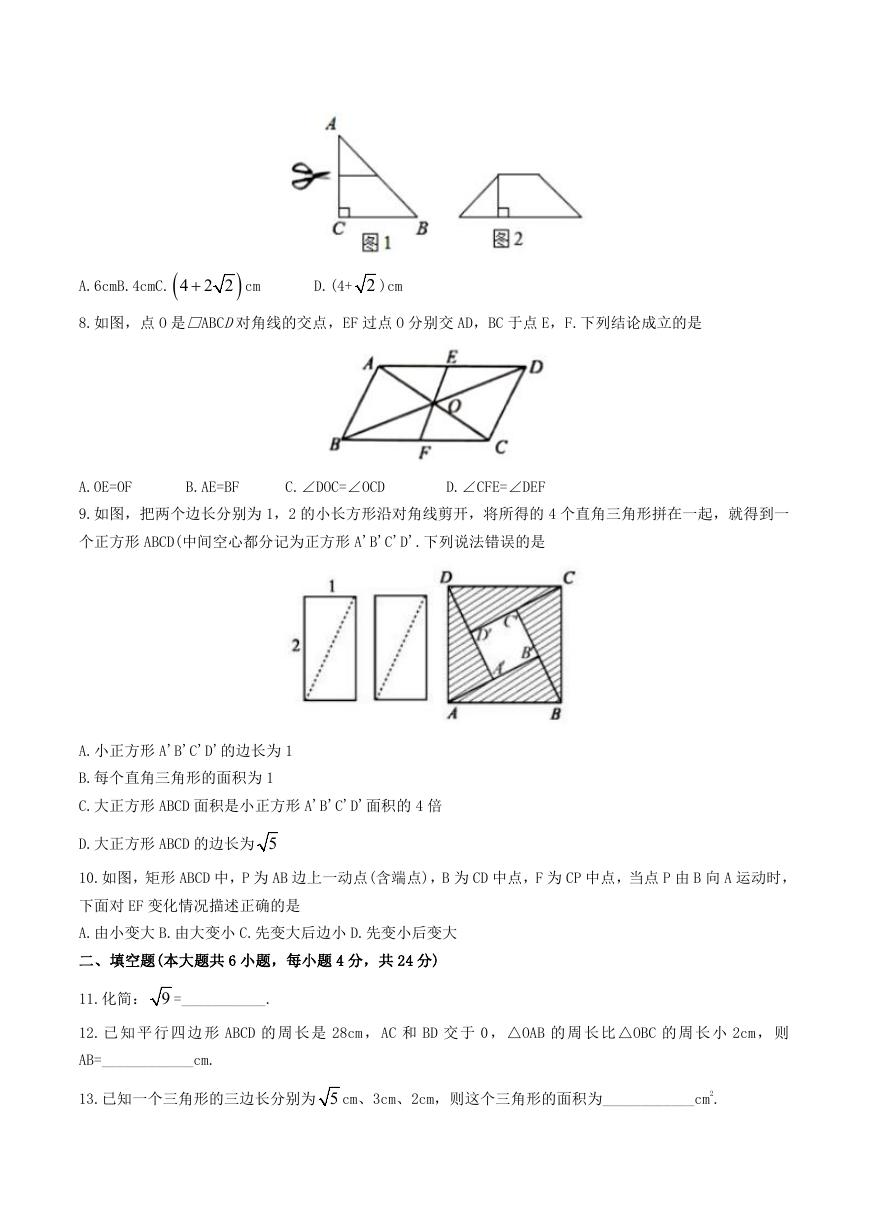2 4.在综合实践活动课上，小明用三根木棒首尾顺次相接摆三角形，下列每组数分别是三根木棒的长度(单位： cm)，其中能摆出直角三角形的一组是 A.32，42，52B.9，12，15C.6，7，8D.4，4，7 5.下列命题中，真命题是 A.两条对角线互相平分的四边形是平行四边形 B.两条对角线互相垂直的四边形是菱形 C.两条对角线互相垂直且相等的四边形是正方形 D.两条对角线相等的四边形是矩形 6.为预防新冠疫情，民生大院入口的正上方 A 处装有红外线激光测温仪(如图所示)，测溢仪离地面的距离 AB=2.4 米米，当人体进入感应范围内时，测温仪就会自动测温并报告人体体温.当身高为 1.8 米的市民 CD 正对门缓慢走到高门 0.8 米的地方时(即测温仪自动显示体温，则人头顶高测温仪的距离 AD 等于 A.1.5 米 B.1.25 米 C.1.2 米 D.1.0 米 7.如图 1 是一张等腰直角三角形纸片，直角边的长度为 2cm，用剪刀沿一直角边和斜边的中点连线(图中虚 线)剪开后，拼成如图 2 的四边形，则该四边形的周长为 学科 网（北 京）股 份有限 公司
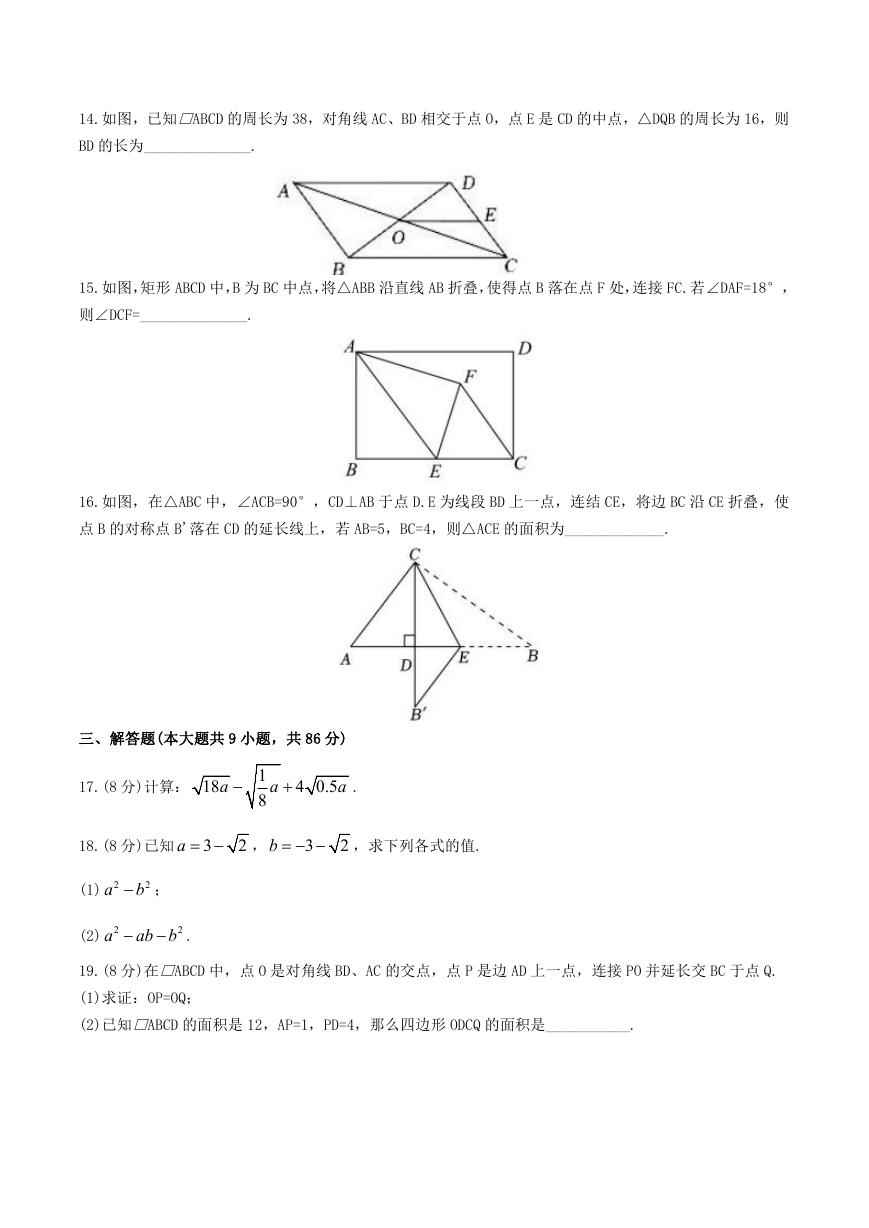
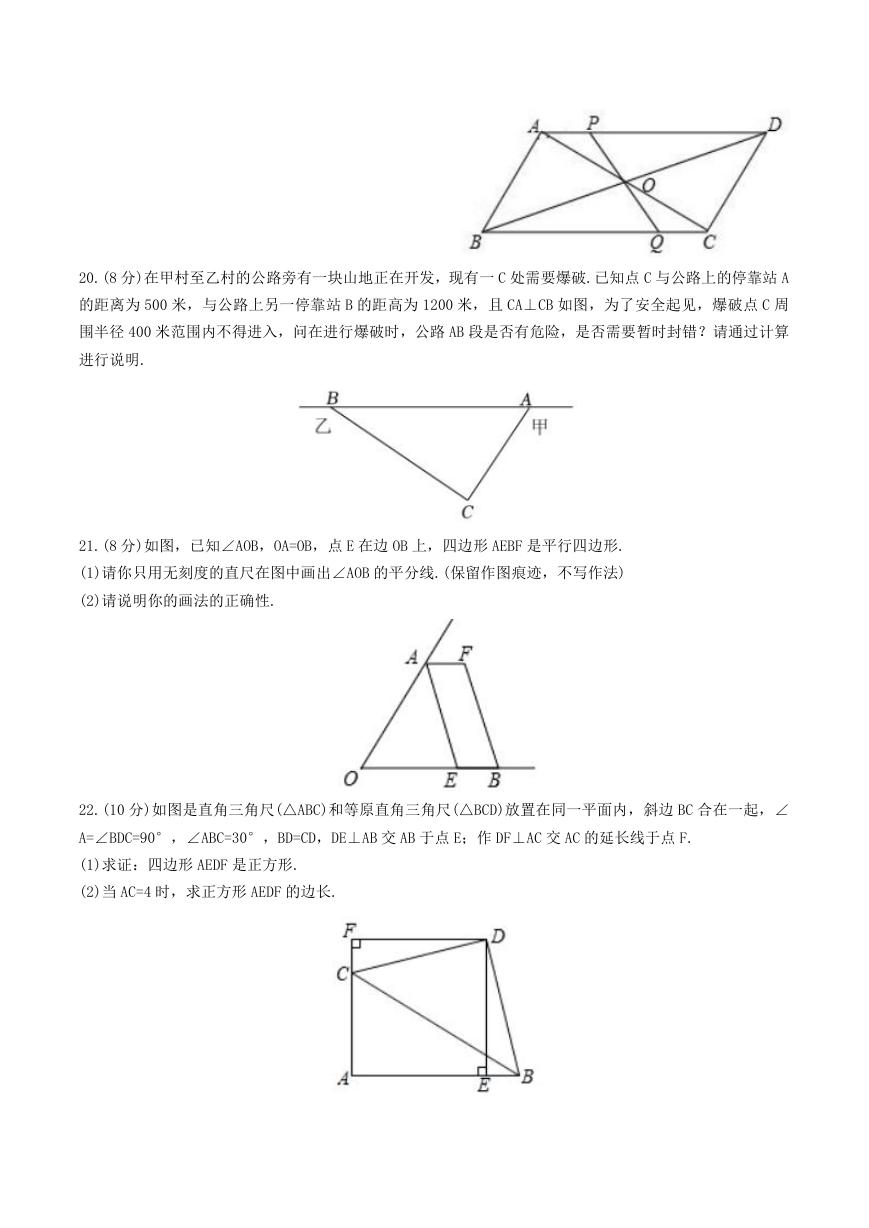
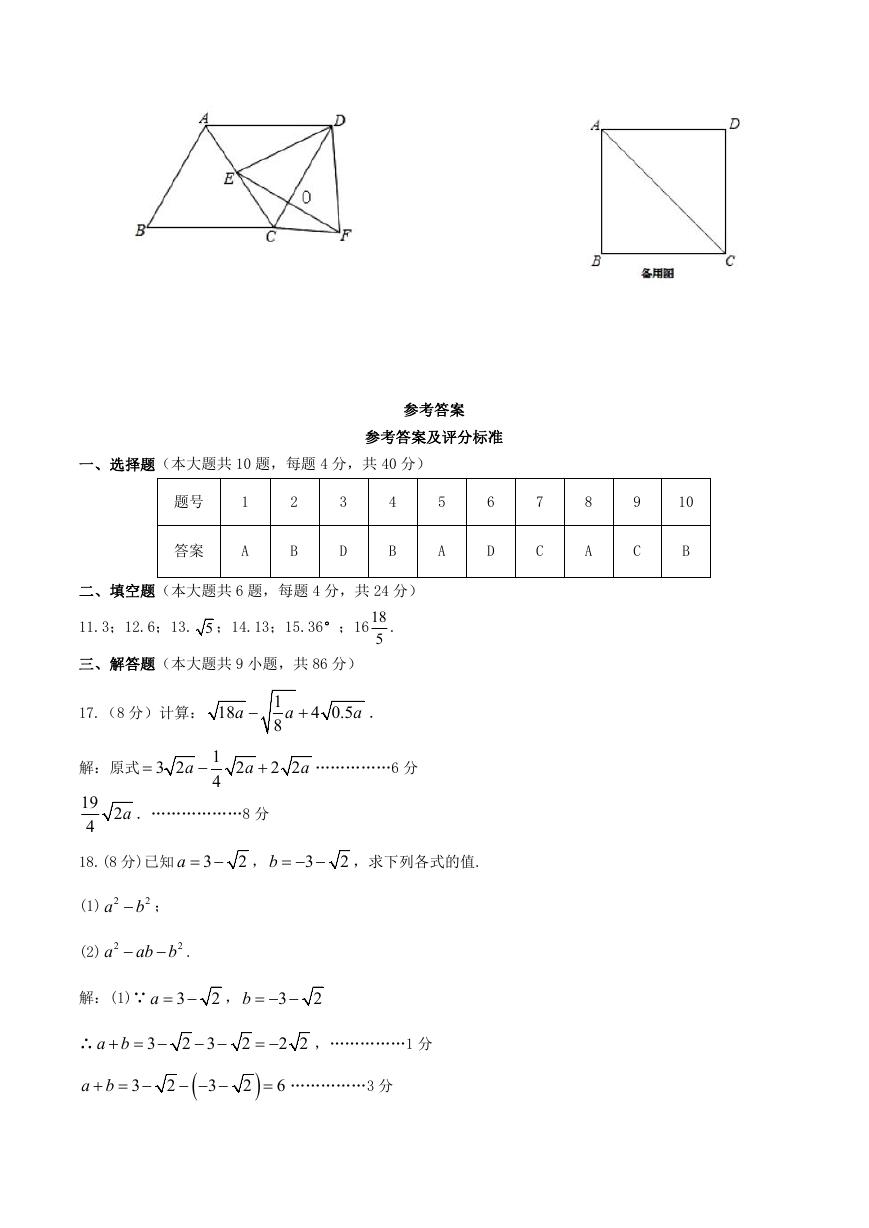
    A.6cmB.4cmC. 4 2 2   cm D.(4+ 2 )cm 8.如图，点 O 是□ABCD对角线的交点，EF 过点 O 分别交 AD，BC 于点 E，F.下列结论成立的是 A.OE=OF B.AE=BF C.∠DOC=∠OCD D.∠CFE=∠DEF 9.如图，把两个边长分别为 1，2 的小长方形沿对角线剪开，将所得的 4 个直角三角形拼在一起，就得到一 个正方形 ABCD(中间空心都分记为正方形 A'B'C'D'.下列说法错误的是 A.小正方形 A'B'C'D'的边长为 1 B.每个直角三角形的面积为 1 C.大正方形 ABCD 面积是小正方形 A'B'C'D'面积的 4 倍 D.大正方形 ABCD 的边长为 5 10.如图，矩形 ABCD 中，P 为 AB 边上一动点(含端点)，B 为 CD 中点，F 为 CP 中点，当点 P 由 B 向 A 运动时， 下面对 EF 变化情况描述正确的是 A.由小变大 B.由大变小 C.先变大后边小 D.先变小后变大 二、填空题(本大题共 6 小题，每小题 4 分，共 24 分) 11.化简： 9 =___________. 12.已 知 平 行 四 边 形 ABCD 的 周 长 是 28cm， AC 和 BD 交 于 0 ， △OAB 的 周 长 比 △OBC 的 周 长 小 2cm， 则 AB=____________cm. 13.已知一个三角形的三边长分别为 5 cm、3cm、2cm，则这个三角形的面积为____________cm2. 学科 网（北 京）股 份有限 公司
    14.如图，已知□ABCD 的周长为 38，对角线 AC、BD 相交于点 O，点 E 是 CD 的中点，△DQB 的周长为 16，则 BD 的长为______________. 15.如图，矩形 ABCD 中，B 为 BC 中点，将△ABB 沿直线 AB 折叠，使得点 B 落在点 F 处，连接 FC.若∠DAF=18°， 则∠DCF=______________. 16.如图，在△ABC 中，∠ACB=90°，CD⊥AB 于点 D.E 为线段 BD 上一点，连结 CE，将边 BC 沿 CE 折叠，使 点 B 的对称点 B'落在 CD 的延长线上，若 AB=5，BC=4，则△ACE 的面积为_____________. 三、解答题(本大题共 9 小题，共 86 分) 17.(8 分)计算： 18 a  1 8 a  4 0.5 a . 18.(8 分)已知 3 a   ， 2 b    ，求下列各式的值. 3 2 (1) 2 a 2 b ； (2) 2 a  ab b  2 . 19.(8 分)在□ABCD 中，点 O 是对角线 BD、AC 的交点，点 P 是边 AD 上一点，连接 PO 并延长交 BC 于点 Q. (1)求证：OP=OQ； (2)已知□ABCD 的面积是 12，AP=1，PD=4，那么四边形 ODCQ 的面积是___________. 学科 网（北 京）股 份有限 公司
    20.(8 分)在甲村至乙村的公路旁有一块山地正在开发，现有一 C 处需要爆破.已知点 C 与公路上的停靠站 A 的距离为 500 米，与公路上另一停靠站 B 的距高为 1200 米，且 CA⊥CB 如图，为了安全起见，爆破点 C 周 围半径 400 米范围内不得进入，问在进行爆破时，公路 AB 段是否有危险，是否需要暂时封错？请通过计算 进行说明. 21.(8 分)如图，已知∠AOB，OA=OB，点 E 在边 OB 上，四边形 AEBF 是平行四边形. (1)请你只用无刻度的直尺在图中画出∠AOB 的平分线.(保留作图痕迹，不写作法) (2)请说明你的画法的正确性. 22.(10 分)如图是直角三角尺(△ABC)和等原直角三角尺(△BCD)放置在同一平面内，斜边 BC 合在一起，∠ A=∠BDC=90°，∠ABC=30°，BD=CD，DE⊥AB 交 AB 于点 E；作 DF⊥AC 交 AC 的延长线于点 F. (1)求证：四边形 AEDF 是正方形. (2)当 AC=4 时，求正方形 AEDF 的边长. 学科 网（北 京）股 份有限 公司
    23.(10 分)如图，斜靠墙上的一根竹竿 AB 长为 10m，端点 B 高墙角的水平距高 BC 长为 6m. (1)已知 A 端沿 AC 向下移动到 A1，AA1=acm，B 端将沿 CB 方向移动到 B1，BB1=bcm，. ①当 a=1 时，求 b 的值； ②当 a b  时，求 a的值. 0 (2)在竹竿滑动的过程中，△ABC 面积有最_______值(填“大”或“小”)，该最值是_______cm2. 24.(12 分)如果一个四边形存在一条对角线，使得这条对角线长度的平方是四边形某两边长度的乘积，则称 这个四边形为“闪亮四边形”，这条对角线称为“亮线”，如图 1，在这个四边形 ABCD 中，AB=AC=AD，满 足 AC2=AB×AD，四边形 ABCD 是内亮四边形，AC 是亮线. (1)以下说法在确的是__________(填写序号) ①正方形不可能是闪亮四边形②矩形有可能是闪亮四边形 ③若一个菱形是闪亮四边形，则必有一个角为 120° (2)如图 2，在四边形 ABCD 中，AD∥BC，∠ABC=90°，AD=9，AB=12，CD=20，四边形 ABCD 是否为闪亮四边 形？如果是，哪条线段是亮线，并写出验证过程，如果不是，说明理由. 25.(14 分)如图，在平行四边形 ABCD 中，点 E 为 AC 上一点，点 E 与点 F 关于 CD 对称. (1)连接 DE，DF，CF，已知 EF 与 CD 交于点 O，ED∥CF. ①求证：四边形 ECFD 是菱形. ②若点 E 为 AC 的中点，求证：AD=EF； (2)若四边形 ABCD 是正方形，连接 BD，BE，BF，当△BDF 是直角三角形时，求 BF BE 的值. 学科 网（北 京）股 份有限 公司
    一、选择题（本大题共 10 题，每题 4 分，共 40 分） 参考答案 参考答案及评分标准 题号 答案 1 A 2 B 3 D 4 B 5 A 6 D 7 C 8 A 9 C 10 B 二、填空题（本大题共 6 题，每题 4 分，共 24 分） 11.3；12.6；13. 5 ；14.13；15.36°；16 三、解答题（本大题共 9 小题，共 86 分） 18 5 . 17.（8 分）计算： 18 a  1 8 a  4 0.5 a ． 解：原式  3 2 a  1 4 2 a  2 2 a ……………6 分 a ．………………8 分 19 2 4 18.(8 分)已知 3 a   ， 2 b    ，求下列各式的值. 3 2 (1) 2 a 2 b ； (2) 2 a  ab b  2 . 解：(1)∵ 3 a   ， 2 3 b    2 2 2 ，……………1 分  ……………3 分 6    ∴ 3 a b   3 a b   2 2 3    3    2 2 学科 网（北 京）股 份有限 公司
    ∴ 2 a  2 b  ( a b a b  )(  )   2 2 6    12 2 ……………4 分 2 (2)∵ 3 a   ，   ab  ∴ 3 2  3 b     2 3   2     ，……………6 分 2 9 7 ∴ 2 a  ab b  2  2 a  2 ab b  2  ab  ( a b  2 )  ab  36 7   ……………8 分 29 19.（8 分）（1）证明：∵四边形 ABCD 是平行四边形， ∴AD∥BC，AO＝CO，……………1 分 ∴∠PAO＝∠QCO，∠APO＝∠CQO……………3 分 ∴△APO≌△CQO，……………4 分 ∴OP＝OQ，……………5 分 （2）四边形 ODCQ 的面积是 3.6.……………8 分 20.（8 分）解：公路 AB 不需要暂时封锁．……………1 分 理由如下：如图，过 C 作 CD⊥AB 于 D． ∵CA⊥CB， ∴∠ACB＝90°，……………2 分 ∵BC＝1200 米，AC＝500 米， ∴根据勾股定理有 AB＝ 1200 2  2 500  130 （米）．……………3 分 ∵S△ABC＝ AB•CD＝ BC•AC……………5 分 1 2 BC AC  AB 1 2 1200 500  1300  6000 13 （米）．……………7 分 ∴CD＝  6000 13 由于 400 米＜ 米，故没有危险，……………8 分 因此 AB 段公路不需要暂时封锁．……………8 分 21.（8 分）解：（1）射线 OP 即为所求，……………4 分 （2）连结 AB、EF 交于点 P，作射线 OP， 学科 网（北 京）股 份有限 公司
    ∵四边形 AEBF 是平行四边形 ∴AP＝BP，……………5 分 又 AO＝BO，OP＝OP，……………6 分 ∴△APO≌△BPO，……………7 分 ∴∠AOP＝∠BOP．……………8 分 22.（10 分）（1）证明：∵DE⊥AB，DF⊥AC ∴∠AED=∠F=90°……………1 分 ∵∠A=90° ∴四边形 AEDF 是矩形……………2 分 ∵∠CDF+∠EDE=∠CDE+∠BED=90° ∴∠CDF＝∠BDE……………3 分   BED 在△BDE 和△CDF 中 CDF  BDE      F   BD CD  ∴△BDE≌△CDF(AAS)，……………4 分   90 ∴DE=DF……………5 分 ∴四边形 AEDF 是正方形．……………6 分 （2）解：∵∠A=90°，∠ABC=30°，AC=4 ∴BC=2AC=8，AB= 2 8  2 4  4 3 ……………7 分 设 CF=BE=x 得 4   x 4 3  x 解得： 2 3 2 x   ……………9 分 ∴正方形 AEDF 的边长是 2 3 2 4    2 3 2  ．……………10 分 23.（10 分）解：（1）①由题意可知△ABC 是直角三角形， 学科 网（北 京）股 份有限 公司
    分享到：
    赞 收藏

    相关推荐

    资料库

    初中二年级

    共收录369份资料，累计95个分类，关注成员有19位，主要包括：2021年,2020年,黑龙江,2022年,贵州,内蒙古,云南,青海,吉林,上海,甘肃,浙江,海南,四川,湖南,广西,山西,山东,辽宁,福建,湖北,河南,河北,江西,广东,安徽,天津,陕西,北京,2019年,江苏

    热门标签

    2021年 2020年 黑龙江 2022年 贵州 内蒙古 云南 青海 吉林 上海 甘肃 浙江 海南 四川 湖南 广西 山西 山东 辽宁 福建 湖北 河南 河北 江西 广东 安徽 天津 陕西 北京 2019年 江苏

    最新资料