第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
2021-2022学年湖北省黄冈市黄梅县八年级下学期期中数学试题及答案.doc
2021-2022 学年湖北省黄冈市黄梅县八年级下学期期中数学试题及答
一、选择题（共 8 小题，每小题 3 分，共 24 分）
1. 下列计算错误．．的是（）．
A. 3 2 2
5 2
C.
2
3
6
案
B.
D.
8
2
8
2
2
2
2. 如图，直线 AO⊥OB，垂足为 O，线段 AO＝3，BO＝4，以点 A为圆心，AB的长为半径画弧，交直线 AO于
点 C．则 OC的长为（）
A. 5
B. 4
C. 3
D. 2
3. 下列说法正确的是（）
A. 平行四边形的对角线互相垂直
B. 矩形的邻边相等
C. 正方形的对角线互相垂直平分
D. 菱形的对角线相等
4. 若
y
x
2
4 2
x
，则
3
(
x
y
)
2022
等于（
）
A. 1
5. 如图，在 Rt ABC
AD 的中点，连接 EF ，若
中，
B. 5
B
90
2 3
，
BAC
AB
，
AD
5
C.
1
，以 AC 为斜边向外作 Rt ACD△
，E 、F 分别为 AC 、
，则 EF 的长为（）
D.
30
2 2
A.
2
B.
3
C. 2
D. 3
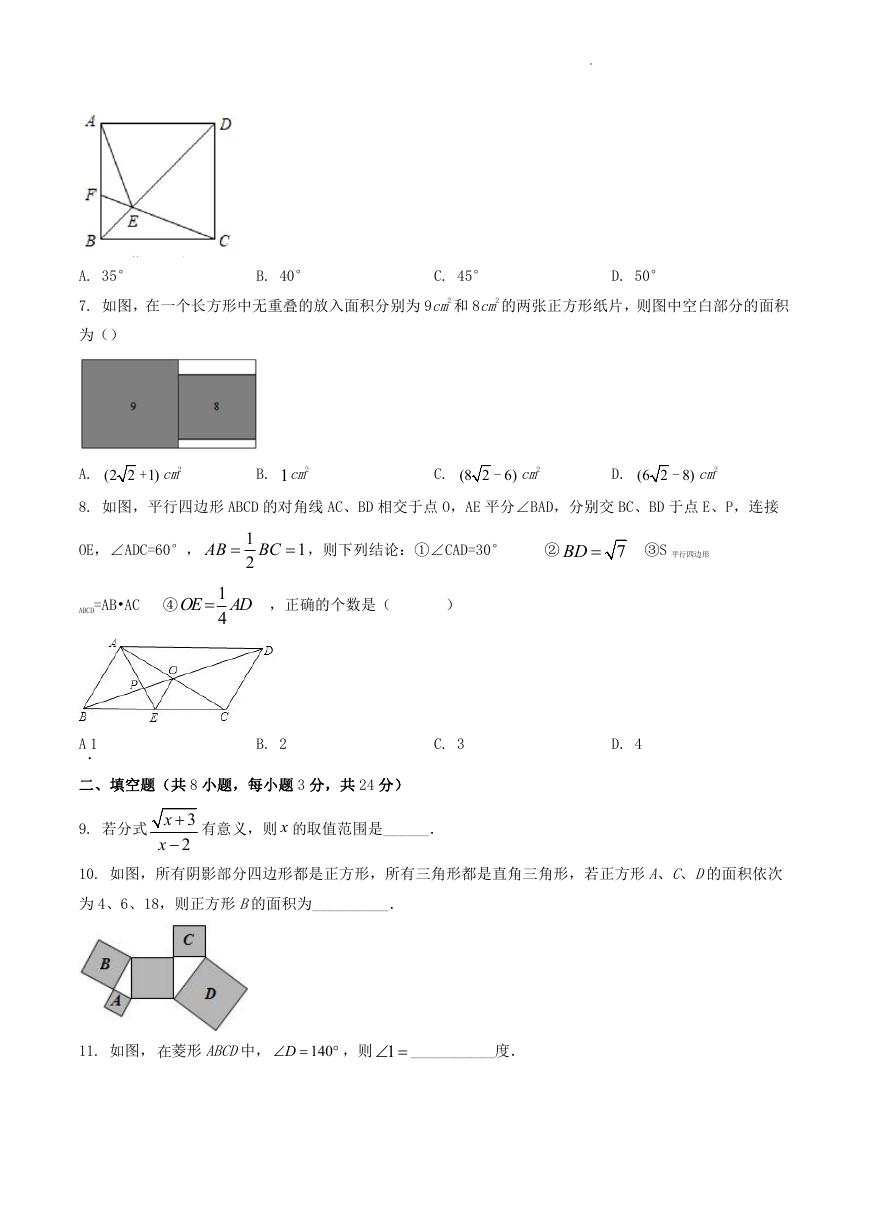
6. 如图，正方形 ABCD中，点 F为 AB上一点，CF与 BD交于点 E，连接 AE，若∠BCF=20°，则∠AEF的度
数（）
学科 网（北 京）股 份有限 公司
A. 35°
B. 40°
C. 45°
D. 50°
7. 如图，在一个长方形中无重叠的放入面积分别为 9cm2 和 8cm2 的两张正方形纸片，则图中空白部分的面积
为（）
A. (2 2 1)+ cm2
B. 1cm2
C. (8 2 6)- cm2
D. (6 2 8)- cm2
8. 如图，平行四边形 ABCD 的对角线 AC、BD 相交于点 O，AE 平分∠BAD，分别交 BC、BD 于点 E、P，连接
OE，∠ADC=60°，
AB
1
2
ABCD=AB•AC ④
OE
AD
1
4
BC
，则下列结论：①∠CAD=30°
1
②
BD
7
③S 平行四边形
，正确的个数是（
）
A.1
二、填空题（共 8 小题，每小题 3 分，共 24 分）
B. 2
C. 3
D. 4
9. 若分式
3
x
2
x
有意义，则 x 的取值范围是______．
10. 如图，所有阴影部分四边形都是正方形，所有三角形都是直角三角形，若正方形 A、C、D的面积依次
为 4、6、18，则正方形 B的面积为__________．
11. 如图， 在菱形 ABCD中，
D
140
，则 1 ___________度．
学科 网（北 京）股 份有限 公司
12. 如图，矩形 ABCD的对角线 AC的垂直平分线分别交 AD、AC、BC于点 E、O、F，若
AB ，
12
BC ，
16
则 EF的长为___________．
13. 如图，《九章算术》中有这样一道古题：今有一竖直着的木柱，在木柱的上端系有绳索，绳索从木柱的
上端顺木柱下垂后堆在地面的部分有三尺（绳索比木柱长 3 尺），牵着绳索退行，在距木柱底部 8 尺（
BC ）
8
处时而绳索用尽．则木柱长为___________尺．
14. 如图，平行四边形 ABCD中，AB>AD，以点 A为圆心，小于 AD的长为半径画弧，分别交 AB，CD于点 E，
F两点；再分别以 E，F为圆心，大于 EF的一半长为半径画弧，两弧交于点 G，作射线 AG交 CD于点 H．若
BC＝12，则 DH＝______．
15. 小明做数学题时，发现
1
1
2
1
2
；
2
2
5
；
2
2
5
3
3
10
3
3
10
；
4
4
17
4
4
17
；…；
按此规律，若
a
8
b
（a，b为正整数），则 a b ___________．
a
8
b
16. 如图，Rt△ABC中，∠C=90°，AC=3，BC=4，点 P为 AB边上任一点，过 P分别作 PE⊥AC于 E，PF⊥BC
于 F，则线段 EF的最小值是_________________．
学科 网（北 京）股 份有限 公司
三、解答题（共 8 小题，满分 72 分）
17. 计算：
（1）
27 3
1
3
12
；
（2）
48
3
1
2
12
24
；
（3）
2 1
2 1
2
．
3 2
18. 计算：
y ，求代数式 2
x
5
5
（1）已知 2
x ， 2
x
（2）先化简，再求值： 2
x
xy
2
的值；
y
2
2
x
2
x
x
1
4
x
4
x
4
x
，其中 2
x ．
2
19. 如图，已知等腰△ABC的底边 BC=10cm，D是腰 AC上一点，且 CD=6cm，BD=8cm．
（1）判断△BCD的形状，并说明理由；
（2）求△ABC的周长．
20. 如图，平行四边形 ABCD的对角线 AC、BD相交于点 O，点 E、F分别为 OD、OB的中点，连接 CE、AF．求
证：CE＝AF．
21. 沙尘暴是指强风将地面尘沙吹起使空气很混浊，水平能见度很低的一种天气现象．人类在发展经济过
程中大肆破坏植被，导致沙尘暴爆发频数增加．如图，某气象局监测到一个沙尘暴中心沿东西方向 AB由 A
学科 网（北 京）股 份有限 公司
向 B移动，已知点 C为一城镇，且点 C与直线 AB上的两点 A，B的距离分别为：
AB
，以沙尘暴中心为圆心周围 25km 以内为受影响区域．
50km
AC
30km
，
BC
40km
，
（1）请通过计算说明城镇 C会受到沙尘暴影响的原因；
（2）若沙尘暴中心的移动速度为 20km/h，则沙尘暴影响该城镇持续的时间有多长？
22. 如图，菱形 ABCD的对角线 AC与 BD交于点 O，分别过点 C、点 D作 BD、AC的平行线交于点 E，连接 EO
交 CD于点 F．
（1）求证：四边形 DECO是矩形；
AC ，
（2）若
23. （1）如图①，四边形 ABCD、CEFG均为正方形．求证： BE DG
BD ，求 EF的长．
6
4
．
（2）如图②，四边形 ABCD、CEFG均为菱形，且 A
明理由；若存在，给出证明．
．是否仍存在结论 BE DG
F
，若不存在，请说
（3）如图③，四边形 ABCD、CEFG均为菱形，点 E在边 AD上，点 G在 AD延长线上．若
AE
ED
2
， A
，
F
学科 网（北 京）股 份有限 公司
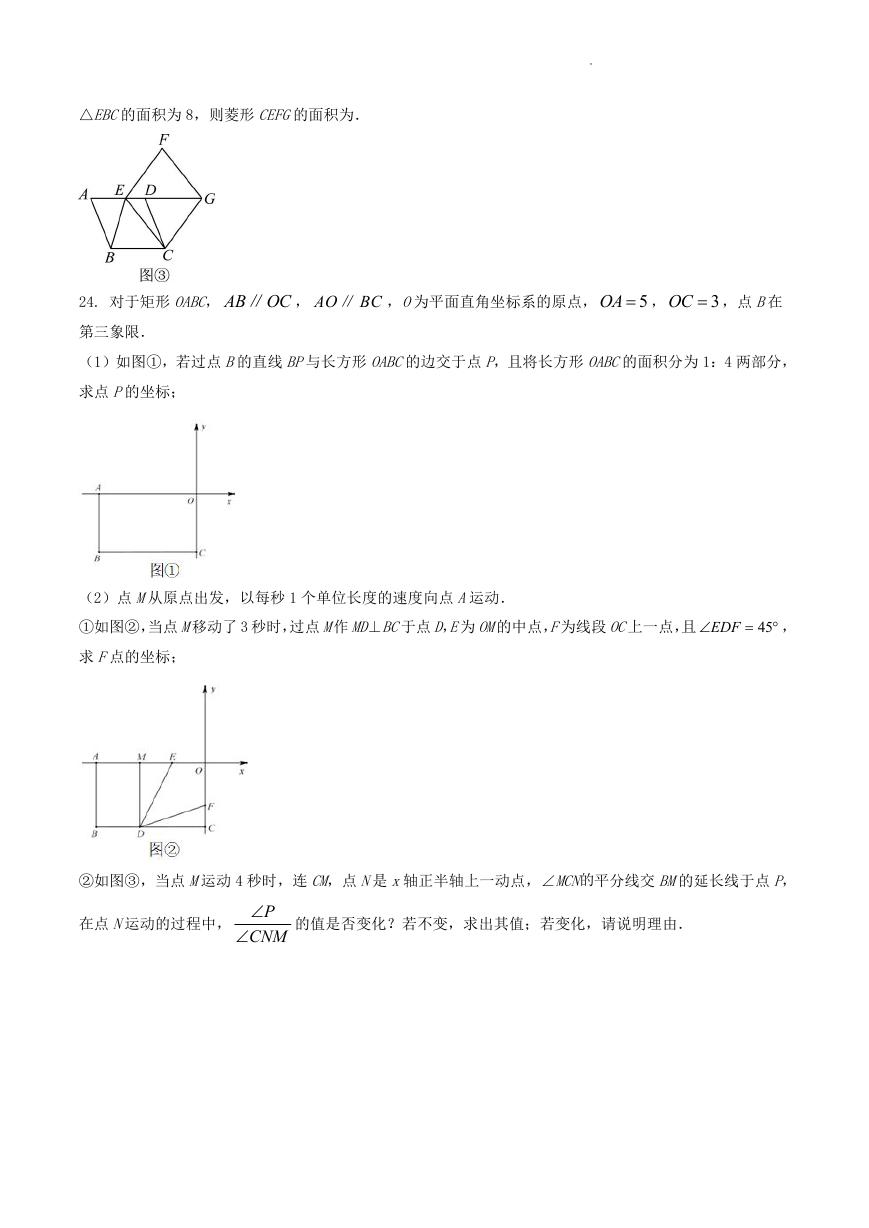
△EBC的面积为 8，则菱形 CEFG的面积为．
24. 对于矩形 OABC， AB OC∥ ， AO BC∥ ，O为平面直角坐标系的原点，
第三象限．
OA ，
5
OC ，点 B在
3
（1）如图①，若过点 B的直线 BP与长方形 OABC的边交于点 P，且将长方形 OABC的面积分为 1：4 两部分，
求点 P的坐标；
（2）点 M从原点出发，以每秒 1 个单位长度的速度向点 A运动．
①如图②，当点 M移动了 3 秒时，过点 M作 MD⊥BC于点 D，E为 OM的中点，F为线段 OC上一点，且
EDF
45
，
求 F点的坐标；
②如图③，当点 M运动 4 秒时，连 CM，点 N是 x轴正半轴上一动点，∠MCN的平分线交 BM的延长线于点 P，
在点 N运动的过程中，
P
CNM
的值是否变化？若不变，求出其值；若变化，请说明理由．
学科 网（北 京）股 份有限 公司
学科 网（北 京）股 份有限 公司
一、选择题（共 8 小题，每小题 3 分，共 24 分）
参考答案
【1 题答案】
【答案】A
【2 题答案】
【答案】D
【3 题答案】
【答案】C
【4 题答案】
【答案】A
【5 题答案】
【答案】A
【6 题答案】
【答案】D
【7 题答案】
【答案】D
【8 题答案】
【答案】D
二、填空题（共 8 小题，每小题 3 分，共 24 分）
【9 题答案】
【答案】
x 且 2
x ##x≠2 且 x≥-3
3
【10 题答案】
【答案】8
【11 题答案】
【答案】20
【12 题答案】
【答案】15
【13 题答案】
【答案】
55
6
【14 题答案】
【答案】12
【15 题答案】
学科 网（北 京）股 份有限 公司
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
