第1页 / 共19页
第2页 / 共19页
第3页 / 共19页
第4页 / 共19页
第5页 / 共19页
第6页 / 共19页
第7页 / 共19页
第8页 / 共19页
2021-2022学年北京丰台四年级上学期期末数学真题及答案.doc
2021-2022 学年北京丰台四年级上学期期末数学真题及答案
一、填空。
1. 302000 是由 3 个（
）和 2 个（
）组成的。
2. 北京市水务局消息，截至 7 月 13 日 5 时，全市水库蓄水量三十一亿六千三百万立方米。
横线上的数写作（
），用“四舍五入”法精确到亿位约是（
）亿立方米。
3. 连接两点可以画出很多条线，其中_____最短。
4. 一个三位数与一个两位数相乘，最大可得（
）位数，最小可得（
）位
数。
5. 要使□76÷87 的商是两位数，□里最小填（
）。
6. 五十年代建成的民族饭店高 47 米，是当时北京的最高建筑，现在“中国尊”是北京市最
高的地标性建筑，高 517 米。“中国尊”的高度大约是民族饭店高度的（
）倍。
7. 如图是由一副三角尺拼成的，∠1 是（
）°。
8. 一个地下车库，有三层。对每个停车位进行了编号，1A003 表示一层 A 区 3 号车位，二
层 C 区 23 号车位的编号是（
）。
9. 如图所示，三条直线相交于一点。已知：∠1＝90°，∠2＝30°。那么，∠3＝（
）°，
∠4＝（
）°。
10. 用 1234 四张数字卡片组成两个两位数，使这两个数的积最大，这两个数分别是
（
）和（
）。
11. ☆表示同一个数，如果☆×14＝126，那么（8＋☆）×14＝（
）。
12. 一块长方形草坪，长 20 米，面积是 110 平方米，如果宽不变，长增加到 100 米，那么
草坪的面积是（
）平方米。
二、选择正确答案前的字母填在（
）里。
13. 下面 4 个数中，最接近 8 万的数是（
）。
A. 69999
B. 76000
C. 79900
D. 80011
14. 下图中有（
）条线段。
A. 4
B. 5
C. 9
D. 10
15. 据天文学家推算，2366 年 9 月 2 日，地球与火星两者之间的距离约为 5571 万千米。下
图中表示这一距离的点是（
）。
A. A
B. B
C. C
D. D
16. 2021 年 9 月 20 日下午 3 时 10 分，搭载天舟三号货运飞船的长征七号遥四运载火箭点
火升空。此时钟面上时针和分针的夹角是（
）。
A. 锐角
B. 钝角
C. 直角
D. 平角。
17. 一个除法算式的被除数、除数都除以 10，商 8 余 7，那么原来的结果是（
）。
A. 商 8 余 7
B. 商 8 余 70
C. 商 80 余 70
D. 商 8 余
56
18. 照这样摆下去，第 6 幅点子图有（
）个点子。
A. 12
B. 13
C. 14
D. 15
19. 小明的笔袋里装有相同型号的红色和黑色签字笔共 3 支，任意摸出一支再放回，摸了 3
次，结果是黑色、红色、红色。如果再摸一次，你认为下面说法正确的是（
）。
A. 一定摸到红色的
C. 可能摸到黑色的
B. 一定摸到黑色的
D. 摸到红色和黑色的可能性一样大
20. 小明用数对（0，1）（4，3）（4，1）表示的是下图（
）中三角形的三个顶点。
A.
C.
B.
D.
21. 画出一个 135°的角，并在图中标出角的度数。
22. 用竖式计算下面各题，并验算第（2）小题。
（1）604×35＝
（2）716＋52＝验算：
23. 计算，怎样简便就怎样算。
（1）166 148 34 352
（3） 63 36 64 63
（2）125 19 8
（4）(103 273 21) 33
24. 看图填空。
（1）首钢滑雪大跳台在首都体育馆（
）方向，距离是（
）千米。
（2）国家游泳中心在首都体育馆（
）方向，距离是（
）千米。
（3）国家速滑馆在国家游泳中心（
）方向。
七、按要求完成下面各题。
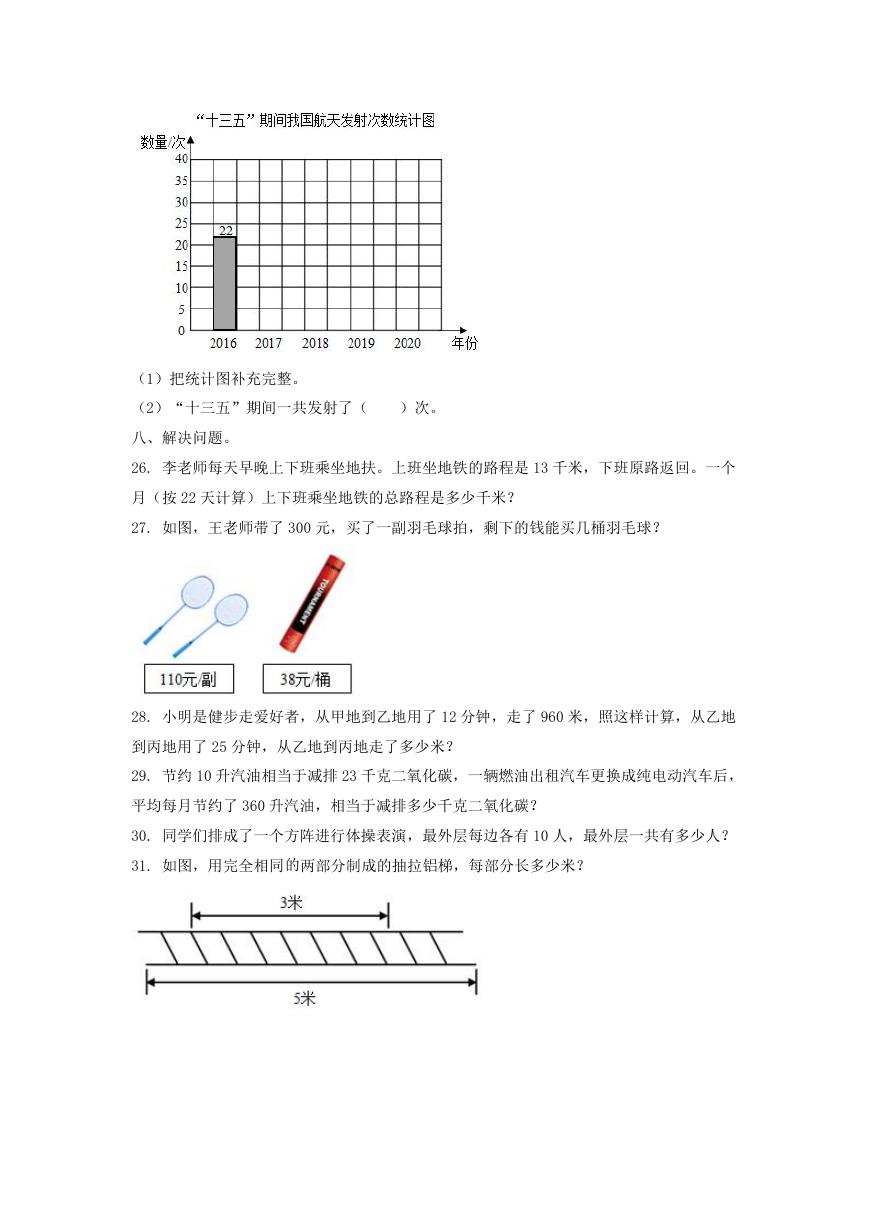
25. “十三五”（2016 年至 2020 年）期间，我国航天事业飞速发展，航天发射次数情况如
下表。
“十三五”期间我国航天发射次数统计表
年份
2016
数量/次
22
2017
18
2018
39
2019
34
2020
39
（1）把统计图补充完整。
（2）“十三五”期间一共发射了（
）次。
八、解决问题。
26. 李老师每天早晚上下班乘坐地扶。上班坐地铁的路程是 13 千米，下班原路返回。一个
月（按 22 天计算）上下班乘坐地铁的总路程是多少千米？
27. 如图，王老师带了 300 元，买了一副羽毛球拍，剩下的钱能买几桶羽毛球？
28. 小明是健步走爱好者，从甲地到乙地用了 12 分钟，走了 960 米，照这样计算，从乙地
到丙地用了 25 分钟，从乙地到丙地走了多少米？
29. 节约 10 升汽油相当于减排 23 千克二氧化碳，一辆燃油出租汽车更换成纯电动汽车后，
平均每月节约了 360 升汽油，相当于减排多少千克二氧化碳？
30. 同学们排成了一个方阵进行体操表演，最外层每边各有 10 人，最外层一共有多少人？
31. 如图，用完全相同的两部分制成的抽拉铝梯，每部分长多少米？
一、填空。
1. 302000 是由 3 个（
）和 2 个（
）组成的。
参考答案
【答案】
①. 十万
②. 千
【解析】
【分析】数位上的数表示有几个该数位的计数单位，据此即可解答。
【详解】302000 是由 3 个十万和 2 个千组成的。
【点睛】掌握整数的数位和计数单位知识是解答本题的关键。
2. 北京市水务局消息，截至 7 月 13 日 5 时，全市水库蓄水量三十一亿六千三百万立方米。
横线上的数写作（
），用“四舍五入”法精确到亿位约是（
）亿立方米。
【答案】
①. 3163000000
②. 32
【解析】
【分析】根据整数的写法：从高位到低位，一级一级地写，哪一个数位上一个单位也没有，
就在那个数位上写 0；省略亿位后面的尾数求近似数，用“四舍五入”法取千万位上近似数，
省略尾数后同时写上“亿”字。
【详解】三十一亿六千三百万写作：3163000000
3163000000≈32 亿
所以北京市水务局消息，截至 7 月 13 日 5 时，全市水库蓄水量三十一亿六千三百万立方米。
横线上的数写作 3163000000，用“四舍五入”法精确到亿位约是 32 亿立方米。
【点睛】此题主要考查整数的写法以及省略亿位后面的尾数求近似数，用“四舍五入”法取
千万位上近似数，省略尾数后同时写上“亿”字。
3. 连接两点可以画出很多条线，其中_____最短。
【答案】线段
【解析】
【详解】两点之间可以画无数条线，根据线段的性质可知：两点之间线段最短；据此解答即
可。
4. 一个三位数与一个两位数相乘，最大可得（
）位数，最小可得（
）位
数。
【答案】
①. 五
②. 四
【解析】
【分析】根据题意，最大的三位数 999，乘最大的两位数 99，可得最大的积；最小的三位数
是 100，乘最小的两位数是 10，可得最小的积，然后再进一步解答。
【详解】最大的三位数 999，最大的两位数 99；最小的三位数是 100，最小的两位数是 10；
999×99＝98901；
100×10＝1000；
98901 是五位数，1000 是四位数；
所以，一个三位数和一个二位数相乘的积，最大可得五位数，最小可得四位数。
【点睛】关键是求出最大与最小的三位数和两位数，然后再进一步解答。
5. 要使□76÷87 的商是两位数，□里最小填（
）。
【答案】8
【解析】
【分析】□76÷87 的商是两位数，那么被除数中的□7 就要大于或等于除数 87，由此找出
由此求出最小的可能；□可以填的数为 8 或 9，进而求解。
【详解】据分析可得：
要使□76÷87 的商是两位数，即□7≥87，□的数只要大于或等于 87 即可，
□里能填 8，9，最小能填 8；
所以要使□76÷87 的商是两位数，□里最小填 8。
【点睛】三位数除以两位数，被除数百位和十位组成的数字和除数比较大小，组成的数字比
除数大或相等，商就是两位数，比除数小，商就是一位数。
6. 五十年代建成的民族饭店高 47 米，是当时北京的最高建筑，现在“中国尊”是北京市最
高的地标性建筑，高 517 米。“中国尊”的高度大约是民族饭店高度的（
）倍。
【答案】11
【解析】
【分析】“中国尊”的高度大约是民族饭店高度的多少倍，用除法计算，据此解答。
【详解】517 47 11
五十年代建成的民族饭店高 47 米，是当时北京的最高建筑，现在“中国尊”是北京市最高
的地标性建筑，高 517 米。“中国尊”的高度大约是民族饭店高度的（11）倍。
【点睛】熟练掌握对倍的认识并灵活应用是解答本题的关键。
7. 如图是由一副三角尺拼成的，∠1 是（
）°。
【答案】75°
【解析】
【分析】一副三角板中的各个角的度数分别是 30°、60°、45°、90°，把它们进行组合
可得到的角有：60°－ 45°＝15°，60°＋45°＝105°，60°＋90°＝150°，90°＋45°
＝135°，90°＋30°＝120°，30°＋45°＝75°，据此即可解答。
【详解】根据以上分析可知， 30°和 45°的角组成 75°的角。
【点睛】本题考查了学生用一副三角板拼成不同角度的能力。
8. 一个地下车库，有三层。对每个停车位进行了编号，1A003 表示一层 A 区 3 号车位，二
层 C 区 23 号车位的编号是（
）。
【答案】2C023
【解析】
【分析】根据题意可知，车位编号的第 1 个数字表示层数，第 2 个字母表示区域号，第 3~5
个数字表示车位。据此可知，二层 C 区 23 号车位的编号中，第 1 个数字是 2，第 2 个字母
是 C，第 3~5 个数字是 023。
【详解】二层 C 区 23 号车位的编号是 2C023。
【点睛】本题考查数字编码问题，关键是明确车位编号中各个数字表示的意义，再进一步解
答。
9. 如图所示，三条直线相交于一点。已知：∠1＝90°，∠2＝30°。那么，∠3＝（
）°，
∠4＝（
）°。
【答案】
①. 60
②. 30
【解析】
【分析】由∠1＋∠2＋∠3 是平角，∠2 和∠4 是对顶角，根据平角是 180°，对顶角相等，
即可解答问题。
【详解】因为∠1＝90°，∠2＝30°，
又因为∠1＋∠2＋∠3＝180°，
所以∠3＝180°－90°－30°，
＝90°－30°，
＝60°，
因为∠2 和∠4 是对顶角，
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
