2023年湖南株洲中考数学真题及答案.doc-资料库

第1页 / 共18页

第2页 / 共18页

第3页 / 共18页

第4页 / 共18页

第5页 / 共18页

第6页 / 共18页

第7页 / 共18页

第8页 / 共18页

2023 年湖南株洲中考数学真题及答案一、选择题（本大题共 10 小题，每小题 4 分，共 40 分） 1．2 的相反数是（） A．2 B．－2 2．计算： 23a  （） C． 1 2 D．  1 2 A．5a B． 23a C． 26a D． 29a 3．计算： 4    （）  3 2 A． 6 B．6 C． 8 D．8 4．从 6 名男生和 4 名女生的注册学号中随机抽取一个学号，则抽到的学号为男生的概率是（） A． 2 5 B． 3 5 C． 2 3 D． 3 4 5．一技术人员用刻度尺（单位：cm ）测量某三角形部件的尺寸．如图所示，已知 ACB  90  ，点 D 为边 AB 的中点，点 A、B 对应的刻度为 1、7，则 CD  （） A．3.5cm B．3cm C． 4cm D． 6cm 6．下列哪个点在反比例函数 y  的图像上？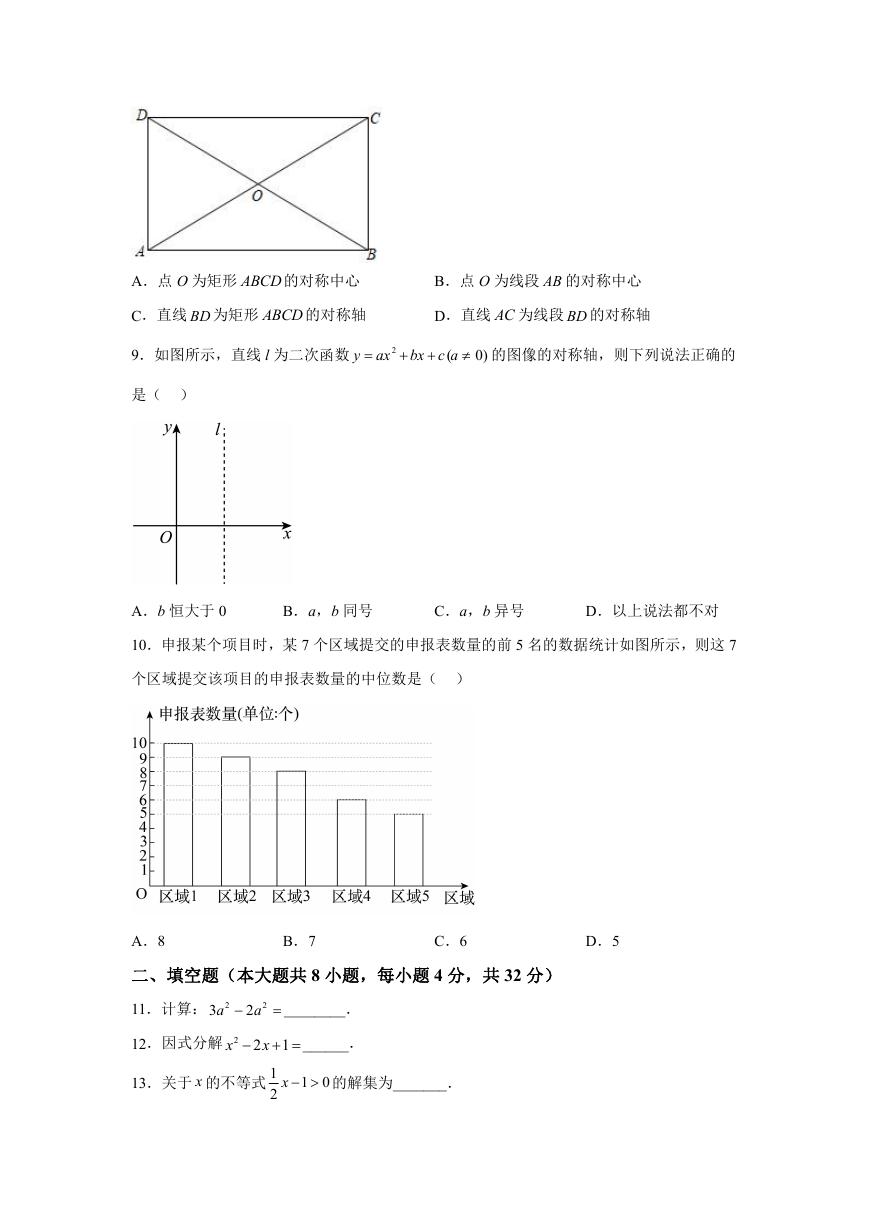（） 4 x A．  1 1, 4 P   B．   2 4, 1 P  C．  3 2,4 P  D．  4 2 2, 2 P  7．将关于 x 的分式方程去分母可得（）  3 2 x B．3 1 1 x  1 2   x A．3 x   3 2 x x C．3 1x   x D．3 3x   x 8．如图所示，在矩形 ABCD 中，AB AD ，AC 与 BD 相交于点 O，下列说法正确的是（）

A．点 O 为矩形 ABCD 的对称中心 B．点 O 为线段 AB 的对称中心 C．直线 BD 为矩形 ABCD 的对称轴 D．直线 AC 为线段 BD 的对称轴 9．如图所示，直线 l 为二次函数 y  2 ax  bx  ( c a  的图像的对称轴，则下列说法正确的 0) 是（） A．b 恒大于 0 B．a，b 同号 C．a，b 异号 D．以上说法都不对 10．申报某个项目时，某 7 个区域提交的申报表数量的前 5 名的数据统计如图所示，则这 7 个区域提交该项目的申报表数量的中位数是（） B．7 A．8 二、填空题（本大题共 8 小题，每小题 4 分，共 32 分） 11．计算： 2 3 a  ________． C．6 2 a 2 D．5 12．因式分解 2 2 x x 13．关于 x 的不等式   ______． 1 1 2 1 0 x   的解集为_______．

14．如图，在平行四边形 ABCD 中， AB  ， 3 BC  ， B 的平分线 BE 交 AD 于点 E，则 DE 5 的长为_____________． 15．如图所示，点 A、B、C 是 O 上不同的三点，点 O 在 ABC 的内部，连接 BO 、 CO ，并延长线段 BO 交线段 AC 于点 D．若   A 60   ， OCD  40  ，则 ODC  _______度． 16．血压包括收缩压和舒张压，分别代表心脏收缩时和舒张时的压力．收缩压的正常范围是： 20 ~140mmHg ，舒张压的正常范围是：60 ~ 90mmHg ．现五人 A、B、C、D、E 的血压测量值统计如下：则这五人中收缩压和舒张压均在正常范围内的人有________个． 17．《周礼考工记》中记载有：“……半矩谓之宣（xuān），一宣有半谓之欘（zhú）……”意 11  宣 2 思是：“……直角的一半的角叫做宣，一宣半的角叫做欘……”．即：1 宣  矩，1 欘 1 2 （其中，1 矩 90  ），问题：图（1）为中国古代一种强弩图，图（2）为这种强弩图的部分组件的示意图，若 1A  矩， 1B  欘，则 C  ______度．

18．已知实数 m、 1x 、 2x 满足： mx 1  2  mx 2   2  ． 4 ①若 m  1 3 ， x 1 9 ，则 2x  _________． ②若 m、 1x 、 2x 为正整数．．．，则符合条件的有序实数．．．．对 ,x x 有_________个 1 2  三、解答题（本大题共 8 小题，共 78 分） 19．计算： 4 2023  0 20．先化简，再求值：     中，点 D、E 分别为 AB AC、的中点，点 H 在线段CE 上，连接 BH ， 21．如图所示，在 ABC 2cos60  1   1  ，其中 3x  ． 1  4  x 2 x 1   x 点 G、F 分别为 BH CH、的中点． (1)求证：四边形 DEFG 为平行四边形 (2) DG BH BD ，   3 ， EF  2 ，求线段 BG 的长度． 22．某花店每天购进16 支某种花，然后出售．如果当天售不完，那么剩下的这种花进行作废处理、该花店记录了10 天该种花的日需求量 n（n 为正整数，单位：支），统计如下表：日需求量 n 13 14 15 16 17 18 天数 1 1 2 4 1 1 (1)求该花店在这10天中出现该种花作废处理．．．．情形的天数； (2)当 16 n  时，日利润 y（单位：元）关于 n 的函数表达式为： 10 n y 80  ；当 16 n  时，日利润为80 元． ①当 14 n  时，间该花店这天的利润为多少元？ ②求该花店这10 天中日利润为 70 元的日需求量的频率．

23．如图所示，在某交叉路口，一货车在道路①上点 A 处等候“绿灯”一辆车从被山峰 POQ 遮挡的道路②上的点 B 处由南向北行驶．已知  POQ  30 线段 AO 的延长线交直线 BC 于点 D． ， ∥ ，OC OQ AO OP BC OQ ，  ， (1)求 COD 的大小； (2)若在点 B 处测得点 O 在北偏西方向上，其中 tan  3 5 ， OD 12 米．问该轿车至少行驶多少米才能发现点 A 处的货车？（当该轿车行驶至点 D 处时，正好发现点 A 处的货车） 24．如图所示，在平面直角坐标系 xOy 中，四边形OABC 为正方形，其中点 A、C 分别在 x 轴负半轴，y 轴负半轴上，点 B 在第三象限内，点  ,0A t ，点  1,2P 在函数 y   k  0 ， x 0  k x 的图像上 (1)求 k 的值； (2)连接、BP CP ，记 BCP  的面积为 S，设 T  2 S 2  ，求 T 的最大值． 2 t 25．如图所示，四边形 ABCD 是半径为 R 的 O 的内接四边形， AB 是 O 的直径， ABD  45  ，直线 l 与三条线段 CD 、CA 、 DA 的延长线分别交于点 E、F、G．且满足 CFE  45  ．

(1)求证：直线l 直线CE ； (2)若 AB DG ； ①求证： ABC △ ≌△ GDE ； ②若 R  1 ， CE 3 2 ，求四边形 ABCD 的周长． 26．已知二次函数 y  2 ax   bx c a   ． 0  (1)若 1  a  ， c ，且该二次函数的图像过点 2,0 ，求b 的值； 1 (2)如图所示，在平面直角坐标系 Oxy 中，该二次函数的图像与 x 轴交于点  A x 1 ,0   B x， 2  ,0 ， x 且 1   ，点 D 在 O 上且在第二象限内，点 E 在 x 轴正半轴上，连接 DE ，且线段 DE x 2 0 交 y 轴正半轴于点 F ，  DOF   DEO OF ， 3 2 DF ． ①求证： DO EO  ． 2 3 ②当点 E 在线段OB 上，且 BE  ． O 的半径长为线段OA 的长度的 2 倍，若 1 4ac   a 2 求 2a b 的值． 2  ， b

参考答案 1．B 【详解】2 的相反数是-2. 故选：B. 2．D 【分析】根据积的乘方法则计算即可． a ． 9 2 【详解】解： 3 a 2 故选：D 3．A 【分析】根据有理数的乘法法则计算即可． 4     ． 6  3 2 【详解】解： 故选：A 4．B 【分析】根据概率公式求解即可．【详解】解：总人数为10 人，随机抽取一个学号共有10 种等可能结果，抽到的学号为男生的可能有 6 种，则抽到的学号为男生的概率为： 6 10  ， 3 5 故选：B． 5．B 【分析】由图求得 AB 的长度，结合直角三角形斜边上的中线等于斜边的一半即可求解．【详解】解：由图可知 AB    7 1 6cm ，在 ACB△ 1 2 CD   中， ACB  90  ，点 D 为边 AB 的中点， AB  3cm , 故选：B． 6．D 【分析】根据反比例函数 y  的图像上的点的横纵坐标乘积为 4 进行判断即可． 4 x

【详解】解：A．∵    1 4  符合题意；    ，∴  1 1, 4 P 4 4   不在反比例函数 y  的图像上，故选项不 4 x B．∵       ，∴   2 4, 1 P 4 4  1 4  不在反比例函数 y  的图像上，故选项不符合题意； 4 x C．∵ 2 4 8     ，∴  3 2,4 P 4  ，∴  4 2 2, 2 P 4 2  D．∵ 2 2  在反比例函数 y  的图像上，故选项符合题意． 4 x 不在反比例函数 y  的图像上，故选项不符合题意； 4 x 故选：D． 7．A 【分析】方程两边都乘以  2 x x  ，从而可得答案．  1 【详解】解：∵ 去分母得：  3 x  3 2 x  1  1  1 x ，  ， 2 x   ， 3 2 x 整理得：3 x 故选 A． 8．A 【分析】由矩形 ABCD 是中心对称图形，对称中心是对角线的交点，线段 AB 的对称中心是线段 AB 的中点，矩形 ABCD 是轴对称图形，对称轴是过一组对边中点的直线，从而可得答案．【详解】解：矩形 ABCD 是中心对称图形，对称中心是对角线的交点，故 A 符合题意；线段 AB 的对称中心是线段 AB 的中点，故 B 不符合题意；矩形 ABCD 是轴对称图形，对称轴是过一组对边中点的直线，故 C，D 不符合题意；故选 A 9．C 【分析】先写出抛物线的对称轴方程，再列不等式，再分 a<0 ， >0a 两种情况讨论即可．【详解】解：∵直线 l 为二次函数 y  2 ax  bx  ( c a  的图像的对称轴， 0) b 2 a >0 ， ∴对称轴为直线 x   当 a<0 时，则 >0b ，当 >0a 时，则 0b  ，

资料库

2023年湖南株洲中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料