第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
2020-2021学年湖南省永州市道县八年级下学期期中数学试题及答案.doc
2020-2021 学年湖南省永州市道县八年级下学期期中数学试题及
答案
温馨提示：
1．本试卷包括试题卷和答题卡。考生作答时，选择题和非选择题都须作答在答题卡上,在本试
卷上作答无效，考生在答题卡上按答题卷中注意事项和要求答题。
2．本试卷满分 150 分，考试时间 120 分钟.本试卷共三道大题，26 个小题。如有缺页，考生
须声明。
一、选择题（本大题共 10 个小题，每小题 4 分，共 40 分，在每小题给出的四个选项中，只有一
项是符合题目要求的，请将你认为正确的选项用 2B 铅笔涂在答题卡上）
1． 以下关于新型冠状病毒的防范宣传图标中是中心对称图形的是（ ）
A．
B．
C．
D．
2． 由下列条件不能判定△ABC 为直角三角形的是（
）
A． A 十 B= C
C．
(
c b c b
)(
)
a
2
3． 如图，一辆货车车厢底板离地面的高度为
3
2
B．a=5，b=12，c=13
D．
a ，
1
3
b ，
1
4
c
1
5
米，为了方便下货，
常 用
一块木板搭成一个斜面，要使斜面与水平地面的夹角不大于
30°，则这块木板的长度至少为（
A．3 米
B．2.5 米
）
C．2.6 米
D．0.87 米.
4． 在□ABCD中，∠A:∠B:∠C:∠D的值可以是（
）
A．1:2:2:1
B．1:2:3:4
C．2:1:1:2
D．2:1:2:1
5．平行四边形、矩形、菱形、正方形都具有的性质是（
）
A．对角线相等
C．对角线平分一组对角
B．对角线互相平分
D．对角线互相垂直
6．如图，已知 AC⊥BD，垂足为 O，AO=CO，AB=CD，则可得到△AOB≌△COD，理由是（
）
A．HL
B．SAS
C．ASA
D．SSS
第 6 题图
第 7 题图
第 8 题图
7． 如图，顺次连接四边形 ABCD各边中点得四边形 EFGH，要使四边形 EFGH为矩形，应添加的条
件是（
A．AB// DC
）
B．AC＝BD
C．AC⊥BD
D．AB＝DC
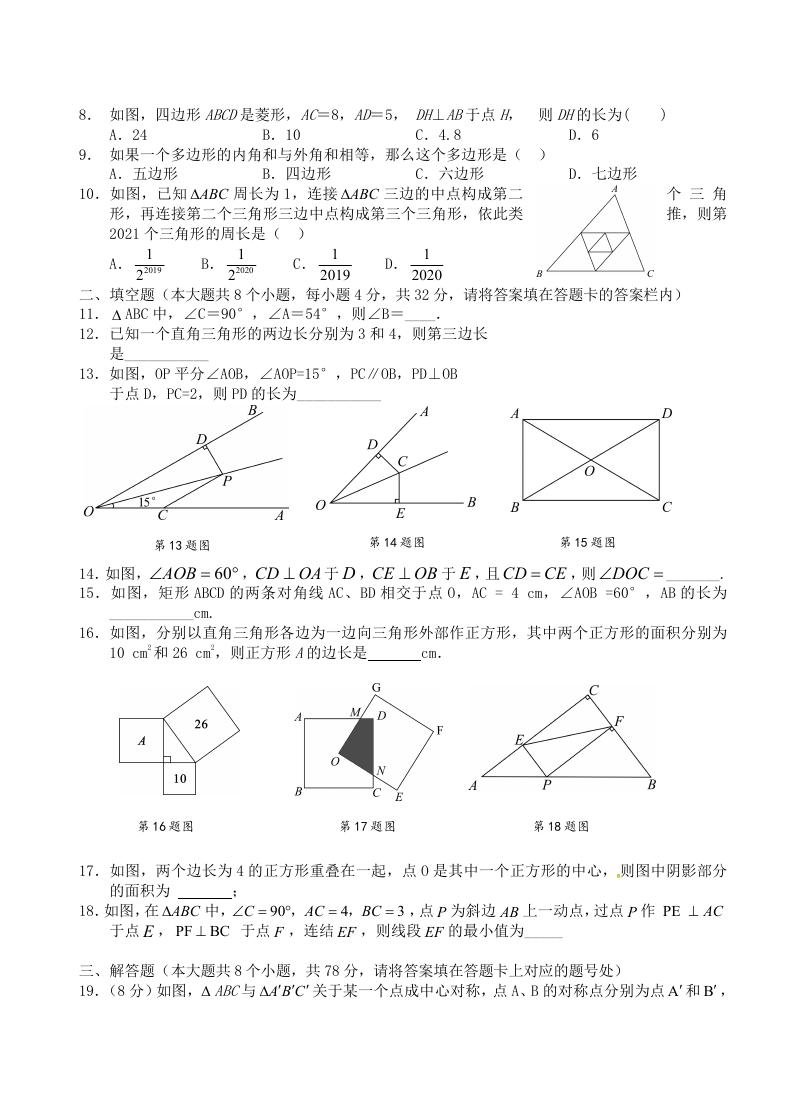
8． 如图，四边形 ABCD是菱形，AC＝8，AD＝5， DH⊥AB于点 H， 则 DH的长为(
)
A．24
B．10
C．4.8
D．6
9． 如果一个多边形的内角和与外角和相等，那么这个多边形是（ ）
A．五边形
B．四边形
C．六边形
D．七边形
10．如图，已知 ABC
三边的中点构成第二
形，再连接第二个三角形三边中点构成第三个三角形，依此类
2021 个三角形的周长是（ ）
周长为 1，连接 ABC
个 三 角
推，则第
1
A． 2019
2
1
B． 2020
2
C．
1
2019
D．
1
2020
二、填空题（本大题共 8 个小题，每小题 4 分，共 32 分，请将答案填在答题卡的答案栏内）
11． ABC 中，∠C＝90°，∠A＝54°，则∠B＝____．
12．已知一个直角三角形的两边长分别为 3 和 4，则第三边长
是___________
13．如图，OP 平分∠AOB，∠AOP=15°，PC∥OB，PD⊥OB
于点 D，PC=2，则 PD 的长为___________
第 13 题图
AOB
第 14 题图
，CD OA 于 D ，CE OB
_______.
14．如图，
15．如图，矩形 ABCD 的两条对角线 AC、BD 相交于点 O，AC = 4 cm，∠AOB =60°，AB 的长为
于 E ，且CD CE ，则 DOC
60
第 15 题图
___________cm.
16．如图，分别以直角三角形各边为一边向三角形外部作正方形，其中两个正方形的面积分别为
10 cm2 和 26 cm2，则正方形 A的边长是
cm．
第 16 题图
第 17 题图
第 18 题图
17．如图，两个边长为 4 的正方形重叠在一起，点 O 是其中一个正方形的中心， 则图中阴影部分
的面积为
18．如图，在 ABC
中，
于点 E ， PF BC
；
C
于点 F ，连结 EF ，则线段 EF 的最小值为_____
90
，
4
，
AC
BC
3
，点 P 为斜边 AB 上一动点，过点 P 作 PE
AC
三、解答题（本大题共 8 个小题，共 78 分，请将答案填在答题卡上对应的题号处）
19．（8 分）如图， ABC与 A B C
关于某一个点成中心对称，点 A、B 的对称点分别为点 A 和 B ，
请找出对称中心 O，同时把图形补充完整．
20．（8 分）工人师傅做铝合金窗框分下面三个步骤进行：
（１）先截出两对符合规格的铝合金窗料，如图（１），使 AB=CD,
（２）摆成如图（２）的四边形，则这时窗框的形状是
EF=CH；
形，根据的数学道理
是
；
（３）将直角尺靠紧窗框的一个角，如图（３），调整窗框的边框，当直角尺的两条直角边
形，根据的数学道理
与窗框无缝隙时，如图（４），说明窗框合格，这时窗框是
是
.
21．（8 分）已知：如图， A ＝ D ＝90 ， AC ＝ BD ．求证：AB=CD．
22.（10 分）如图，一艘渔船以 40 海里/小时的速度由西向东追赶鱼群，在 A 处测得小岛 C 在渔
船的北偏东 60 方向；半小时后，渔船到达 B 处，此时测得小岛 C 在渔船的北偏东 30°方向．已
知以小岛 C 为中心，周围 18 海里以内为军事演习着弹危险区．如果这艘渔船继续向东追赶鱼
群，是否有着弹危险？
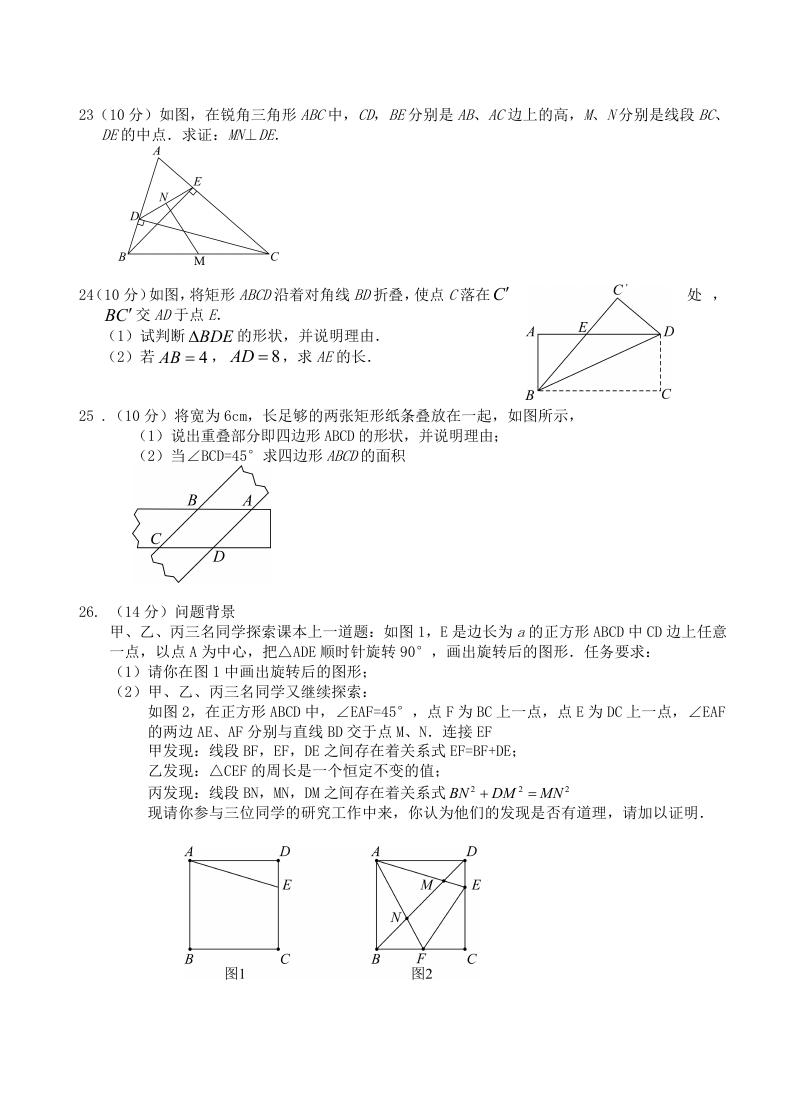
23（10 分）如图，在锐角三角形 ABC中，CD，BE分别是 AB、AC边上的高，M、N分别是线段 BC、
DE的中点．求证：MN⊥DE．
24（10 分）如图，将矩形 ABCD沿着对角线 BD折叠，使点 C落在C
BC 交 AD于点 E．
（1）试判断 BDE
AB ，
（2）若
4
的形状，并说明理由．
AD ，求 AE的长．
8
处 ，
25 .（10 分）将宽为 6cm，长足够的两张矩形纸条叠放在一起，如图所示，
（1）说出重叠部分即四边形 ABCD 的形状，并说明理由；
（2）当∠BCD=45°求四边形 ABCD的面积
26. （14 分）问题背景
甲、乙、丙三名同学探索课本上一道题：如图 1，E 是边长为 a的正方形 ABCD 中 CD 边上任意
一点，以点 A 为中心，把△ADE 顺时针旋转 90°，画出旋转后的图形．任务要求：
（1）请你在图 1 中画出旋转后的图形；
（2）甲、乙、丙三名同学又继续探索：
如图 2，在正方形 ABCD 中，∠EAF=45°，点 F 为 BC 上一点，点 E 为 DC 上一点，∠EAF
的两边 AE、AF 分别与直线 BD 交于点 M、N．连接 EF
甲发现：线段 BF，EF，DE 之间存在着关系式 EF=BF+DE；
乙发现：△CEF 的周长是一个恒定不变的值；
丙发现：线段 BN，MN，DM 之间存在着关系式 2
BN
现请你参与三位同学的研究工作中来，你认为他们的发现是否有道理，请加以证明．
DM MN
2
2
八年级数学参考答案及评分标准
一、选择题(每小题 4 分，共 40 分)
1. A.
二、填空题（每小题 4 分，共 32 分）
2. D .
3. A.
4. D
5. B
6. A
7. C
8.C
9.B
10. B
11. 36°
12. 5 或 7
13. 1
14. 30°
15. 2
16. 4
17. 4
18.
2.4
（ 12
5
）
三、解答题（共 78 分）
19. (8 分) 解：作法：①连接
和
，交于点 ，则点 就是对称中心， ………4 分
②连接 并延长至 ，使 C O CO
，
………6 分
③连接
，则
就是对称三角形．
………8 分
20. (8 分)解：平行四边形 两组对边分别相等的四边形是平行四边形
矩形
有一个角是直角的平行四边形是矩形
21. (8 分)证明：连接 BC
………4 分
………8 分
………1 分
∵ A ＝ D ＝90 ， AC ＝ BD ， BC ＝ BC ，
∴
Rt BAC Rt CDB HL
∴AB=CD
22. (10 分)根据题意，
AB
40
，
20
1
2
………6 分
………8 分
CAB
30
，
CBD
60
， ………2 分
∴
∴
A
CB
BC AB
CB
D
20
，
CA
B
30
，
………5 分
BCD
90
60
30
，
在 Rt BCD
2
BD
BC
∴
10
BD ，
∴
中，
，
∴
CD
2
BC
2
BD
2
20
2
10
300 18
，
答：如果这艘渔船继续向东追赶鱼群有着弹危险．
………7 分
………9 分
………10 分
23. (10 分)证明：如图，连接 DM，ME，
∵CD、BE分别是 AB、AC边上的高，
M是 BC的中点.
∴DM＝ BC，ME＝ BC，
………2 分
………4 分
∴DM＝ME，
又∵N为 DE中点，
∴MN⊥DE；
是等腰三角形，理由如下：
DBC
，
24. (10 分)
（1） BDE
由折叠得： EBD
∵四边形 ABCD是矩形，
∴ / /
∴ ADB
∴ ADB
∴ BE DE
∴ BDE
AD BC ，
DBC
EBD
，
，
，
（2）解：设 AE x ，则
是等腰三角形．
BE DE
，
8
x
90
A
∵四边形 ABCD是矩形，
，
∴
∴在 Rt ABE△
即 2
(8
4
x
x ，
3
解得： 3
AE ．
∴
中， 2
AB
，
x
)
2
2
2
AE
2
BE
，
25. (10 分)
（1）如图重叠部分的形状为：菱形
证明： ∵ 两张纸条都是矩形,
∴ AB∥CD, BC∥AD.
∴ 四边形 ABCD 是平行四边形，
………3 分
分别过 B、D 作 BE⊥CD于点 E，DF⊥CB于点 F,
∵两纸条等宽
∴BE=DF=6
………6 分
………10 分
………1 分
………5 分
………10 分
………1 分
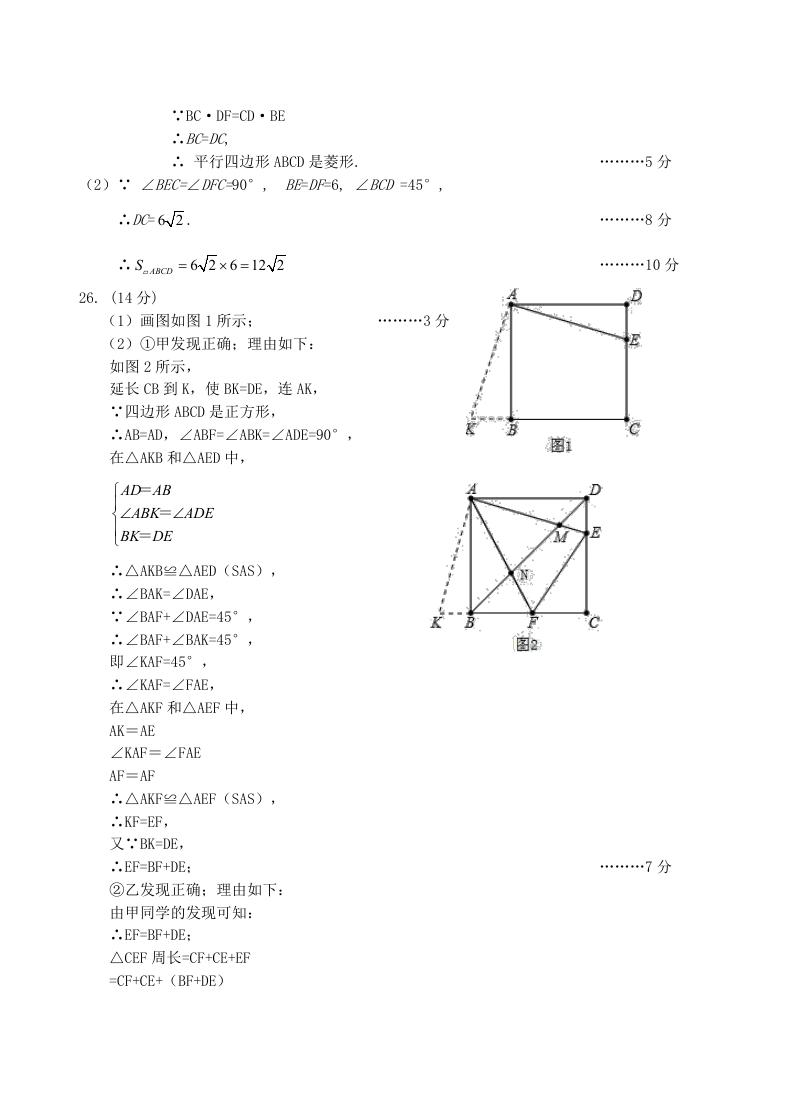
∵BC·DF=CD·BE
∴BC=DC,
∴ 平行四边形 ABCD 是菱形.
（2）∵ ∠BEC=∠DFC=90°, BE=DF=6, ∠BCD =45°,
∴DC= 6 2 .
∴
S
ABCD
6 2 6 12 2
26. (14 分)
（1）画图如图 1 所示；
（2）①甲发现正确；理由如下：
………3 分
如图 2 所示，
延长 CB 到 K，使 BK=DE，连 AK，
∵四边形 ABCD 是正方形，
∴AB=AD，∠ABF=∠ABK=∠ADE=90°，
在△AKB 和△AED 中，
AD AB
＝
BK DE
＝
ABK
＝
ADE
∴△AKB≌△AED（SAS），
∴∠BAK=∠DAE，
∵∠BAF+∠DAE=45°，
∴∠BAF+∠BAK=45°，
即∠KAF=45°，
∴∠KAF=∠FAE，
在△AKF 和△AEF 中，
AK＝AE
∠KAF＝∠FAE
AF＝AF
∴△AKF≌△AEF（SAS），
∴KF=EF，
又∵BK=DE，
∴EF=BF+DE；
②乙发现正确；理由如下：
由甲同学的发现可知：
∴EF=BF+DE；
△CEF 周长=CF+CE+EF
=CF+CE+（BF+DE）
………5 分
………8 分
………10 分
………7 分
=（CF+BF）+（CE+DE）
=BC+DC=2a（定值）；
③丙发现正确；理由如下：
如图 3，在 AK 上截取 AG=AM，连接 BG，GN，
在△ABG 和△ADM 中，
AG＝AM
∠KAB＝∠EAD
AB＝AD
∴△ABG≌△ADM（SAS），
∴BG=DM，∠ABG=∠ADB=45°，
又∵∠ABD=45°，
∴∠GBD=90°，
∵∠BAF+∠DAE=45°，
∴∠KAF=45°，
∴∠KAF=∠FAE，
在△GAN 和△NAM 中，
AG＝AM
∠KAF＝∠FAE
AN＝AN
∴△GAN≌△NAM（SAS），
∴NG=MN，
∵∠GBD=90°，
∴BG2+BN2=NG2，
∴BN2+DM2=MN2；BN2+DM2=MN2
………10 分
………14 分
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
