第1页 / 共50页
第2页 / 共50页
第3页 / 共50页
第4页 / 共50页
第5页 / 共50页
第6页 / 共50页
第7页 / 共50页
第8页 / 共50页
《概率论与数理统计》讲义笔记.pdf
考点
重要程度
分值
常见题型
连续型
二维随机变量
1.概率密度
必考
大题
2.边缘概率密度
3.条件概率密度
4.独立性
高斯课堂 大学课程辅导中心
官方贴吧：高斯课堂
课时一 事件的运算及概率
重要程度
必考
★★★
分值
6 ~ 10
3 ~ 6
常见题型
选择、填空
选择、填空
考点
1.事件及运算
2.古典概型
3.几何概型
1. 事件及运算
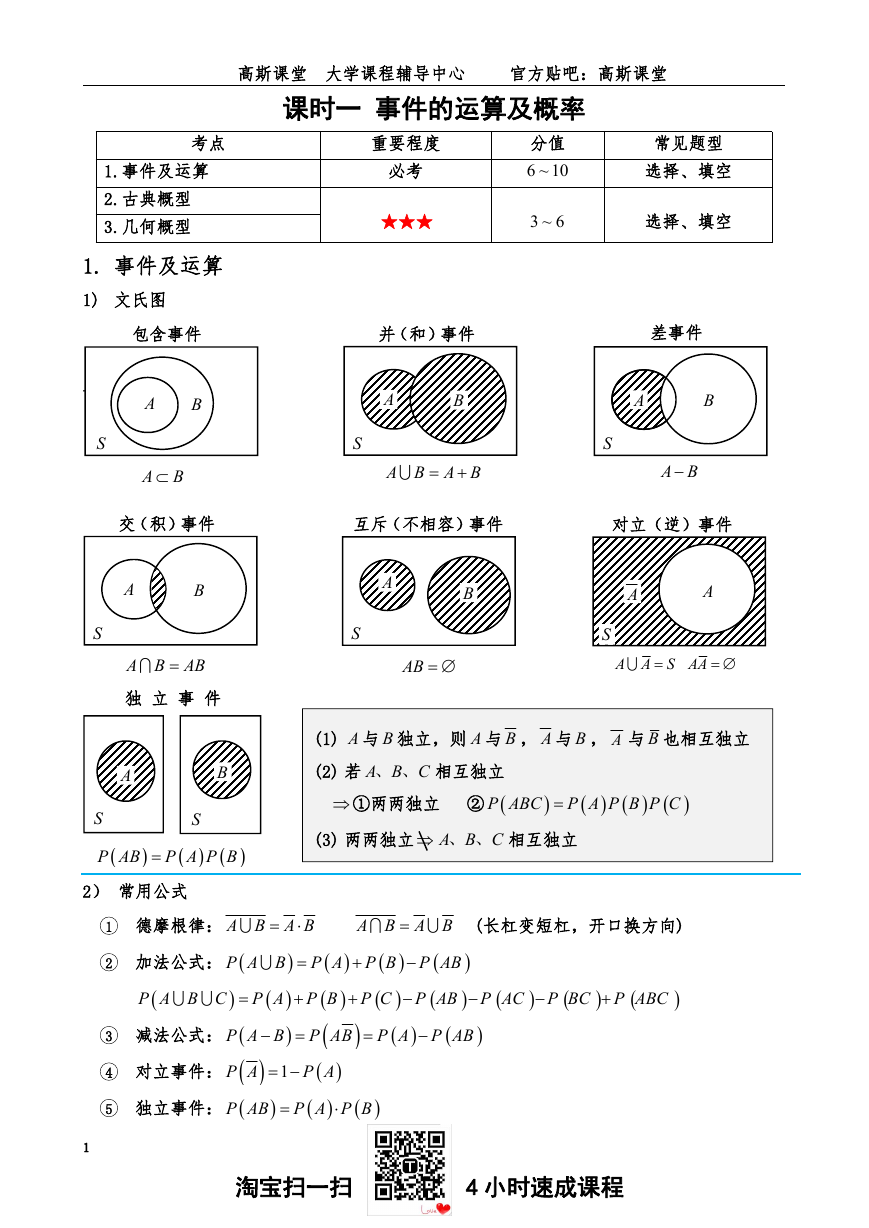
1) 文氏图
包含事件
并（和）事件
差事件
+
S
A
B
A B
A
B
S
A B A B
A
B
S
A B
交（积）事件
互斥（不相容）事件
对立（逆）事件
A
B
A B AB
独 立 事 件
A
B
S
S
S
P AB
P A P B
2） 常用公式
A
B
S
AB
A
A
S
A A S AA
(1) A 与 B 独立，则 A 与 B ， A 与 B ， A 与 B 也相互独立
(2) 若 A B C、 、 相互独立
①两两独立 ②
(3) 两两独立 A B C
、 、 相互独立
P A P B P C
P ABC
P A B C
1 德摩根律： A B A B
2 加法公式：
P A B
P A
3 减法公式：
P A B
4 对立事件：
P A
5 独立事件：
P AB
1
P A
P B
P AB
P A
P A P B
A B A B
P AB
P AC
P AB
P B
P AB
P C
P A
(长杠变短杠，开口换方向)
P BC
P ABC
11
淘宝扫一扫
4 小时速成课程
高斯课堂 大学课程辅导中心
官方贴吧：高斯课堂
题 1.事件 A B C、 、 中至少有一个事件发生可以表示为 A B C
。
题 2.设
P A
0.4
,
P B
0.3
,
P AB
0.1
,则
P A B
______。
解： (
P A B
)
P A
)
(
P B
(
)
P AB
(
）＝ ＋
0.4 0.3 0.1 0.6
＝
题 3.已知
P A
P B
P C
,
P AB
1
7
P BC
1
14
,
P AC 则 A B C、 、 中至少有一
0
个发生的概率_______。
解：
P A
P A B C
P B
P C
P AB
P BC
P AC P ABC
+
1
1
7
1
1
7 14 14
0 0
2
7
1
7
题 4.若
解：
P A ，
P B
0.4
P A B
P A B
1
0.5
, A B、 互斥，则
P A B
_______。
P A B
1
P A
P B
P AB
1 0.4 0.5 0 0.1
题 5. A B、 相互独立，
P A ，
P A B
0.3
0.6
，
P B _______。
解： (
P A B
)
P A
(
)
P B
(
)
P AB
(
)
P A
P B
P A P B
0.6
0.3
P B
(
) 0.3 (
P B
) 0.6
题 6.若
P B ，
P A B
0.3
3
7
0.4
P B
(
)
，则
0.3
P A B
_______。
P A
P B
P AB
P A
P AB
0.4
解：
P A B
P A B
P A
P AB
0.4 0.3 0.1
P AB ，则
=0
题 7.设
A . A 和 B 互不相容
P A 或
C .
P B
=0
=0
B . A 和 B 对立
D .
P A B
P A
解： A 错：若 A 和 B 互不相容
P AB
=0
，但
P AB AB
=0
B 和C 错： A B、 独立，
P AB P A P B 不一定等于 0
=
D 正确：
P A B
P A
P AB
P A
22
淘宝扫一扫
4 小时速成课程
高斯课堂 大学课程辅导中心
官方贴吧：高斯课堂
2. 古典概型
题 1.在一箱子中共有 7 个球，3 个黑球 4 个白球，求：
⑴从中无放回抽取3 个球，求 A “取得两黑一白”的概率；
⑵从中有放回抽取3 个球，求 B “取得两黑一白”的概率。
n
!
n
(
n
1)
1
0! 1
解：
P A
=
1
4
2
C C
3
3
C
7
12
35
C
m
n
n
n
1
m
!
n m
1
P B C
=
2
3
2
3
7
3
4
7
2
3
7
4 108
7 343
=
C
1
n
C
1n
n
n
n
!
m n m
!
!
题 2.一箱产品有 a 个正品，b 个次品，甲先取一个（取后不放回），乙再取一个，问乙取到正
品的概率。
P
解：若甲取的为正品，乙取得正品概率： 1
a b a b
a
1
a
1
P
若甲取的为次品，乙取得正品概率： 2
a
b
a b a b
1
P P P
2
1
a b a b
a
1
a
a
b
a b a b
1
a
a b
1
注：此类问题中，“一次取
出 k 个”和“逐次无放回
取出 k 个”，第i 次抽取的
时候和第一个人对应的概
率是一样的，比如最典型
的：抽奖。
3. 几何概型
题 1.设 x 的取值范围为
1,6 ，问 2
5x 的概率为_______。
解：
P
(2
x
5)
3
5
1
2
3
4
5
6
x
题 2.两个人相约 7 点至8 点到某地点会面，先到者等另一人 20 分钟，过时就可以离去，试求
两个人能会面的概率。
解：设两人到达的时间分别为 x ， y ，两个人会面的事件为 A 。
A
则
P A
=1
x
y
20
40 40 5
60 60 9
=
y
60
x
y
20
x
y
20
20
20
60
x
33
淘宝扫一扫
4 小时速成课程
高斯课堂 大学课程辅导中心
官方贴吧：高斯课堂
课时一 练习题
1. 设事件 A B、 互不相容，已知
P A
=0.4
，
P B
=0.5
,则
P A B
=
若 A B、 独立，则
P A B
2. 已知 A B、 是两个独立的事件，其中
P A
=0.7
，
P B
=0.3
，则
P A B
=
3. 已知
P A
=0.5
，
P A B
=0.7
,若 A B、 独立，则
P B
4. A B、 为随机事件，若
P A B
=0.5
，
P A
=0.3
，则
P B A
5. 甲袋中有 4 只红球，有 6 只白球，乙袋中有 6 只红球，10 只白球，现从两袋中各任取1球，
则 2 个球颜色相同的概率是（）
.A 6
40
.B 15
40
.C 21
40
.D 19
40
6. 甲、乙两门高射炮彼此独立地向一架飞机各发一炮，甲、乙击中飞机的概率分别为 0.3 和
0.4 ，则飞机至少被击中一炮的概率为____
7. 掷 2 颗均匀的骰子，两个点数之和为 7 的概率为____
8. 设随机变量 A 为
5,7
x 上的均匀分布，则关于 x 的方程 29
x
6
Ax A
有实根的
6 0
概率为
44
淘宝扫一扫
4 小时速成课程
高斯课堂 大学课程辅导中心
课时二 全概率公式、贝叶斯公式
官方贴吧：高斯课堂
考点
1.条件概率、乘法公式
2.全概率、贝叶斯公式
重要程度
必 考
分值
51~10
常见题型
大 题
1. 条件概率、乘法公式
题 1.投一颗骰子，事件 A 为“点数大于 3 ”，事件 B 为“点数为5 ”。则 (
P B A _______。
)
解：
P AB
(
)
P B
(
)
1
6
P A
(
)
1
2
P B A
(
)
P AB
(
)
P A
)
(
1
6
1
2
1
3
条件概率：
P B A
(
)
P A B
(
)
P AB
(
)
P A
)
(
P AB
(
)
P B
)
(
乘法公式：
P A P B A
P AB
(
)
)
(
P B P A B
(
)
)
)
(
(
区别： (
)P B 样本空间为点数
1,2,3,4,5,6 ，
P B
(
1
)= 6
P B A 样本空间为点数
A
(
)
4,5,6
，
P B A
(
1
)= 3
题 2.已知 (
P A ， (
) 0.6
P B A ，则 (
) 0.3
P AB _______。
)
解： (
P AB
)
P A P B A
(
)
(
) 0.6 0.3 0.18
题 3.已知 (
P A B
) 0.8
， (
P B ，则 (
) 0.4
P A B _______。
)
解：
P A B
(
)
)
P A B
(
P B
)
(
P A P AB
(
)
)
P B
(
(
)
P A B
(
)
P A P B
(
(
)
)
P AB
(
) 0.4
得 (
P A P AB
)
(
) 0.4
P B
(
) 1
P B
(
) 1 0.4 0.6
P A P AB
(
)
(
) 0.8
P A P AB
(
)
P B
(
(
)
)
0.4
0.6
2
3
故
P A B
(
)
55
淘宝扫一扫
4 小时速成课程
高斯课堂 大学课程辅导中心
官方贴吧：高斯课堂
2. 全概率公式、贝叶斯公式
题 1.甲、乙、丙三车间加工同一产品，加工量分别占总量 25% ， 35% ， 40% ，次品率分别
为 0.03， 0.02 ，0.01 ，现从所有产品中抽取一个产品，试求：
⑴该产品是次品的概率?
⑵若检查该产品是次品，求该产品是乙车间生产的概率？
解：①设事件 A 为该产品是次品
② 1B 为甲厂生产， 2B 为乙厂生产， 3B 为丙厂生产
全概率公式解题：
1 设 A 为发生的事件
2 找出完备事件组 iB
③ 1
P B
(
)
1
4
P B
(
)
2
7
20
P B
(
)
3
2
5
3 写出 (
)iP B 及 (
P A B
)i
4 代入全概率公式：
P A B
(
) 0.03
1
P A B
(
) 0.02
2
P A B
(
) 0.01
3
P A
(
)
n
i
1
P B P A B
(
i
)
(
i
)
)
贝叶斯（逆概）公式:
)
(
i
P A
)
(
P B A
(
)
P B P A B
(
i
5
i
④
P A
)
(
P B P A B
(
1
)
(
1
)
P B P A B
(
2
)
(
2
)
P B P A B
(
3
)
(
3
)
1
4
0.03
7
20
0.02
2
5
0.01
37
2000
⑤
P B A
)
(
2
P B P A B
(
2
2
(
)
P A
(
)
)
7
20
0.02
37
2000
14
37
题 2.设工厂 A 和工厂 B 的产品的次品率分别为1% 和 2% ，现从由 A 和 B 的产品分别占 60% 和
40% 的产品中，随机抽取一件发现是次品，则该次品属于 A 厂生产的概率是多少？
解：设事件 A 为“抽取一件为次品”
1B 为从 A 工厂生产， 2B 为从 B 工厂生产
P B ， 2(
1(
) 0.6
P B
) 0.4
P A B ，
(
) 0.01
1
P A B
(
) 0.02
2
P B P A B
(
1
)
(
1
)
P B P A B
(
2
)
(
2
) 0.6 0.01 0.4 0.02 0.014
P B P A B
(
1
1
)
(
P A
(
)
)
0.6 0.01
0.014
3
7
则
P A
)
(
P B A
(
)
1
66
淘宝扫一扫
4 小时速成课程
高斯课堂 大学课程辅导中心
官方贴吧：高斯课堂
题 3.盒中有 4 个红球，6 个黑球，今随机地取出一球，观察颜色后放回，并加上同色球 2 个，
再从盒中第二次抽取一球，求：
⑴第二次取出的是黑球的概率；
⑵已知第二次取出的是黑球，求第一次取出的也是黑球的概率。
解：⑴设事件 A 为“第二次取出的是黑球”
1B 为第一次取出是红球， 2B 为第一次取出是黑球
P B
(
)
1
4
10
P B
(
)
2
6
10
P A B
(
)
1
6
12
P A B
(
)
2
8
12
则
P A
)
(
P B P A B
(
1
)
(
1
)
P B P A B
(
2
)
(
2
)
6
6
4
3
10 12 10 12 5
+
=
8
⑵
P B A
)
(
2
P B P A B
(
2
2
)
(
P A
(
)
)
6
8
10 12
3
5
2
3
课时二 练习题
1. 已知
P A
0.8
,
P B
0.4
,且 A B ,则
P B A
2. 设 A B、 是两个随机事件，且
0
P A
1,
P B
P B A
,则必有（ ）
0
. C A B
. D P A
P B
4. 仓库中有10 箱同种规格的产品，其中 2 箱、3 箱、5 箱分别由甲、乙、丙三个厂生产，三
个厂的正品率分别为 0.7,0.8,0.9 ，现在从这10 箱产品中任取一箱，再从中任取一件
(1) 求取出的产品为正品的概率
(2) 如果取出的是正品，求此件产品由乙厂生产的概率
5. 某保险公司把被保险人分为3 类：“谨慎的”、“一般的”、“冒失的”，统计资料表明，这 3
种人在一年内发生事故的概率依次为 0.05,0.15,0.30 ；如果“谨慎的”被保险人占 20% ，
“一般的占50% ，“冒失的”占 30% ，问：
(1) 一个被保险人在一年内出事故的概率是多大？
(2) 若已知某被保险人出了事故，求他是“谨慎的”类型的概率。
77
淘宝扫一扫
4 小时速成课程
. B P B A
. D P AB
0,
P A B
P B A
P A P B
. A P A B
. C P AB
P A B
P A P B
1
3. 设 ,A B 满足
P B A 则（ ）
B P B A
.
. A A 是必然事件
高斯课堂 大学课程辅导中心
官方贴吧：高斯课堂
课时三 一维随机变量
考点
重要程度
分值
常见题型
离散型随机变量
连续型随机变量
1.分布律、分布函数
2.函数的分布
3.概率密度、分布函数
★★★
★★★
必 考
4.函数的分布
★★★★
6~3
选择、填空
01~6
大 题
1.离散型随机变量分布律、分布函数
题 1.盒中有 6 个球，其中 4 个白球， 2 个黑球，从中任取 2 个球，求：
(1) 抽到白球数 X 的分布律； （2）随机变量 X 的分布函数
解：⑴ X 可取 0 ，1， 2
0
2
C C
4
2
2
C
6
P X
0
X
P
0
1
15
1
8
15
1
15
2
6
15
P X
1
1
1
C C
4
2
2
C
6
8
15
P X
2
2
0
C C
4
2
2
C
6
6
15
⑵ 0
x 时， ( ) 0
F x
0
1x 时，
F x
( )
1
x 时，
2
F x
( )
2
x 时， ( ) 1
F x
1
15
1
8
15 15
9
15
F x
( )
0
1
15
9
15
1
x
0
0
x
1
1
x
2
2
x
分布函数：
( )F x
P X x
①0
F x
( ) 1
② (
F , (+ ) 1
F
) 0
③ ( )F x 单调不减函数
④右连续
F x
lim ( )
x
x
0
F x
(
0
)
题 2.设随机变量 X 的分布函数为
F x
x
1
0
x
1
1
0.4
x
3
0.8 1
x
3
1
，求 X 的分布律和
P
1
X
3
X
P
1
0.4
1
0.4
3
0.2
分布函数求分布律：
①先写分断点
1
P
X
3
P X
1
P X
3
0.4 0.2 0.6
②分段点处概率减去上一个概率
解：
88
淘宝扫一扫
4 小时速成课程
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
