logo资料库

基于NSST和改进数学形态学的遥感图像目标边缘提取.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：1.04M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    2017年 8月 图 学 学 报 August2017第38卷 第4期 JOURNAL OF GRAPHICS Vol.38No.4 收稿日期：2016-11-28；定稿日期：2017-01-25 基金项目：国家自然科学基金项目(61573183)；CAD&CG国家重点实验室开放基金项目(A1519)；城市空间信息工程北京市重点实验室开放基金项目(2014203)；港口航道泥沙工程交通行业重点实验室开放基金项目；水利部黄河泥沙重点实验室开放基金项目(2014006)；城市水资源与水环境国家重点实验室开放基金项目(LYPK201304)；江苏高校优势学科建设工程资助项目 第一作者：吴诗婳(1992–)，女，江苏南京人，硕士研究生。主要研究方向为图像处理。E-mail：wshimage@163.com 通信作者：吴一全(1963–)，男，江苏启东人，教授，博士，博士生导师。主要研究方向为图像处理与识别。E-mail：nuaaimage@163.com 基于NSST和改进数学形态学的遥感图像 目标边缘提取 吴诗婳1， 吴一全1,2,3,4,5,6， 周建江1 (1. 南京航空航天大学电子信息工程学院，江苏 南京 211106； 2. 浙江大学CAD&CG国家重点实验室，浙江 杭州 310058； 3. 城市空间信息工程北京市重点实验室，北京 100038； 4. 南京水利科学研究院港口航道泥沙工程交通行业重点实验室，江苏 南京 210024； 5. 黄河水利委员会黄河水利科学研究院水利部黄河泥沙重点实验室，河南 郑州 450003； 6. 哈尔滨工业大学城市水资源与水环境国家重点实验室，黑龙江 哈尔滨 150090) 摘要：为了从遥感图像中提取出更为准确完整的目标边缘，提出一种基于无下采样Shearlet模极大值和改进数学形态学的目标边缘提取方法。首先采用无下采样Shearlet变换(NSST)将图像分解成边缘细节丰富的高频分量和边缘细节较少的低频分量；然后结合不同分解程度下边缘像素点处的系数关系，对高频分量的各个子带进行模极大值检测，再经过双层掩膜筛选后得到高频边缘提取结果；对低频分量采用改进的数学形态学方法，得到低频边缘提取结果；最后将上述两部分融合，使用区域连通方法去除孤立点，得到最终的目标边缘图像。大量实验结果表明，与Canny以及其他4种同类边缘提取方法相比，本文方法所得边缘定位准确、完整清晰、细节丰富，且抗噪能力强，为后续遥感图像目标特征提取与识别奠定更好基础。 关键词：目标边缘提取；遥感图像；无下采样Shearlet变换；数学形态学；区域连通 中图分类号：TP 391.41；TP 751.1 DOI：10.11996/JG.j.2095-302X.2017040523 文献标识码：A 文 章 编 号：2095-302X(2017)04-0523-08 Target Edge Extraction of Remote Sensing Images Based on Non-Subsampled Shearlet Transform and Improved Mathematical Morphology WU Shihua1, WU Yiquan1,2,3,4,5,6, ZHOU Jianjiang1 (1. College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu 211106, China; 2. State Key Laboratory of CAD&CG, Zhejiang University, Hangzhou Zhejiang 310058, China; 3. Beijing Key Laboratory of Urban Spatial Information Engineering, Beijing 100038, China; 4. Key Laboratory of Port, Waterway and Sedimentation Engineering of the Ministry of Transport, Nanjing Hydraulic Research Institute, Nanjing Jiangsu 210024, China; 5. Key Laboratory of the Yellow River Sediment of Ministry of Water Resource, Yellow River Institute of Hydraulic Research, Yellow River Water Resources Commission, Zhengzhou Henan 450003, China; 6. State Key Laboratory of Urban Water Resource Environment, Harbin Institute of Technology, Harbin Heilongjiang 150090, China)
    524 视觉与图像 2017年 Abstract: In order to extract edges of target area more completely and accurately from remote sensing images, a method of target edge extraction is proposed based on improved mathematical morphology and modulus maxima of non-subsampled Shearlet transform. Firstly, the image is decomposed into high-frequency components with more edges and details and low-frequency component with fewer edges and minutiae through non-subsampled Shearlet transform. Then considering the property of coefficients of edge points under different decomposing conditions, the modulus maximum detection is performed for each sub-band of high-frequency components and the double-layer mask is adopted afterwards so as to get the high-frequency edge extraction result. Moreover, the low-frequency component is processed through the improved mathematical morphology method to get the low-frequency edge extraction result. Finally, the above two parts are fused and the final target edge image is obtained after removing the isolated points according to the regional connectivity. A large number of experimental results show that, compared with Canny method and four similar edge extraction methods, the detected edges by the proposed method are accurate, clear, complete and with abundant details. The method has strong anti-noise performance, which lays a better foundation for the following target feature extraction and recognition of remote sensing images. Keywords: target edge extraction; remote sensing images; non-subsampled Shearlet transform; mathematical morphology; regional connectivity 遥感图像的多时相、多角度、多平台、多光谱等特点，为人类认识整个地球表面的地貌、地况提供了可靠、高效的数据保障[1]。对遥感图像中的目标区域进行边缘提取，是遥感数据应用与信息挖掘中一项非常重要的工作，也是后续遥感图像分割与描述、特征提取与分类识别的前提与基础，在海岸线保护[2]、水资源调查[3]、河流监测[4]、城市建筑物规划[5]等方面有着重要的实际应用。 现有的遥感图像边缘提取方法通常是基于空间域或变换域，前者主要利用Sobel[6]、Prewitt[7]、LOG[8]、Canny[9]等微分算子以及形态学等手段提取图像中的边缘。基于微分算子的方法依据一阶或二阶微分提取边缘点，通过选择合适的阈值对边缘点进行筛选，从而实现对目标的边缘提取。Canny算法以其严格的提取标准以及较高地提取准确性，逐渐取代了其他边缘提取算子[10]，在遥感图像边缘提取中得到广泛应用，但其微分运算的抗干扰能力较差，使得提取出的边缘仍存在漏检、虚警和断裂现象[11]。基于集合论发展而来的数学形态学方法相比上述几类微分算子，所提取的边缘结果更优[12]。该方法中常用的腐蚀和膨胀算子虽然可以保证提取的边缘较平滑，但腐蚀算子所得边缘信号较强，抗干扰性不足；而膨胀算子得到的边缘信号较弱，易出现边缘模糊现象[13]。另一方面，后者主要在遥感图像的变换域内进行操作，从而提取的是图像边缘[14]。目前，一般通过小波、Contourlet、无下采样Contourlet、Shearlet等变换对遥感图像的高频分量进行处理，滤除高频分量中的伪边缘及干扰成分，以此提取遥感图像的目标边缘。其中小波变换由于对图像中的方向信息表示较差，无法准确地提取图像中的边缘信息[15]。Contourlet变换在一定程度上弥补了此类缺陷，但因其需要进行下采样操作，随之而来易导致出现伪吉布斯现象[16]。随后，文献[17-18]提出利用无下采样Contourlet变换(non-subsampled Contourlet transform, NSCT)对图像进行分解并提取边缘，消除伪吉布斯现象，所得目标边缘较完整、清晰，但由于NSCT采用方向滤波器组实现多方向，方向的选择性受限于图像的分解尺度，表示的方向数目有限，且计算效率较低。文献[19]将Shearlet变换应用于遥感图像边缘提取中，相比其他多尺度变换方法，该方法能更好地表达遥感图像中的边缘细节轮廓信息，但仍无法避免下采样操作，使得其不具有平移不变性。 鉴于上述分析，本文提出了一种基于无下采样Shearlet变换(non-subsampled Shearlet transform, NSST)模极大值和改进数学形态学的遥感图像目标边缘提取方法。NSST变换是近年来受到较多关注的多尺度几何分析工具，对高维几何结构具有近乎最优的表示性能[20]。本文通过NSST提取
    第4期 吴诗婳，等：基于NSST和改进数学形态学的遥感图像目标边缘提取 525 图像的高频分量和低频分量，对不同尺度、不同方向的高频子带，采用非模极大值抑制的方法得到高频目标边缘提取结果；另一方面，采用改进的双结构元素数学形态学方法对分解后的低频分量进行处理，以此得到低频目标边缘提取结果；最后将高低频边缘提取结果加权融合，并使用区域连通方法去除孤立噪声点，得到最终的目标边缘提取结果。针对多幅遥感图像进行了大量实验，并与Canny[10]、基于优化核的边缘滤波[14]、基于小波变换与边缘跟踪[15]、基于NSCT模极大值与Canny[17]、基于NSCT模极大值与数字形态学[21]等5种边缘提取方法相比较，给出了相应的评价。 1 无下采样Shearlet变换 NSST是基于Shearlet的一种改进，能够更为准确地描述图像特征。图1是NSST的分解流程图，包括多尺度和多方向分解(虚线框)。前者采用无下采样金字塔(non-subsampled Pyramid, NSP)对图像逐层划分；后者通过改进的剪切滤波器(Shearlet filter, SF)对每一层高频分量进行方向细分。NSST的多尺度分解过程与NSCT类似，对图像进行j次NSP分解后，得到与原图像尺寸相同的(j+1)个分量，包括1个低频分量(最底层)和j个高频分量。NSST的多方向分解过程主要通过改进的SF实现，最后经过逆傅里叶变换和二维卷积完成。由此避免了标准SF中需要进行下采样操作的问题，能有效克服Shearlet变换产生的伪吉布斯效应，具有平移不变性以及更好的方向性。 图1 NSST分解流程图 合成膨胀仿射系统(维数为2)表示为 1/2,,()()|det()|()ljjlCxxCABΜABA (1) 式中，22()L为尺度参数，,jl为剪切参数，分别控制着NSST的尺度分解数目和方向分解数目；2C为平移参数；各向异性膨胀矩阵A、剪切矩阵B均为22的可逆矩阵，且det1B。22()fL，若2,,,,|,|||||jlCjlCff，则称()ABΜ中的元素为合成小波。 NSST是合成小波的一种特殊情况，其中4002A，1101B，小波函数Clj,,的频域支撑区间为 (0)12,,21242421121ˆsupp{(,):[2,2][2,2],/22}jlCjjjjjjl≤ (2) 式(2)中，NSST频域支撑区间可以近似看作大小222jj、斜率2jl的梯形对，图2分别给出了NSST的频域剖分图与相应地频域支撑区间。 (a) NSST频域剖分图 (b) NSST频域支撑区间 图2 NSST频域剖分图和频域支撑区间 2 基于NSST和改进数学形态学的遥感图像目标边缘提取方法原理及具体步骤 2.1 基于NSST模极大值的高频分量目标边缘提取 在对遥感图像进行NSST分解后，本文采用模极大值检测手段提取高频分量的目标边缘细节信息。鉴于NSST的特性，高频分量的各个方向子带所代表的边缘纹理走向均由SF决定，则每一个方向上的模极大值点必定在该方向子带中。因此，无需像传统的模极大值方法一样通过计算模的相位角确定边缘梯度的方向，基于NSST的模极大值方法可直接对高频分量方向子带中的像素点进行较为简便的非模极大值抑制处理，通过比较中心像素点与其8-邻域的模值，从而选取局部模极大值。
    526 视觉与图像 2017年 图3是模极大值检测方向示意图，图中每个像素点处的边缘方向数为8。由于边缘方向具有对称性，可以将相差180°的两个边缘方向合为一个，只需考虑其中4个方向的边缘。因此，在进行基于NSST模极大值的高频分量目标边缘提取时，应选择合适的剪切参数l。过多的方向分解只会增加算法的复杂度，对边缘提取效果并无显著提升，而过少的方向分解则无法提取出边缘的细节信息。 图3 模极大值检测方向示意图 利用NSST对遥感图像进行j次NSP分解和l级方向分解后，可以得到j个高频分量，各个高频分量中的任意像素点均有(22)l个与原图像尺寸相同的方向子带。本文中，j=3，各层高频分量的l值均为3，相应的方向分解个数为10。设NSST分解的第p层、第q个方向子带上像素点(,)mn的模值为,(,)pqMmn，依据式(3)，即比较该像素点与其领域内在边缘垂直方向上的两个像素点模值大小，可判定该像素点是否为局部模极大，以此对非模极大值点进行抑制，使边缘更加突出。 ,,,,,,(,)(,),(,)(1,1)and(,)(1,1)0,elsepqpqpqpqpqpqMmnMmnMmnMmnMmnMmn≥≥(3) 通常情况下，NSST分解的层数越多，每层高频分量中像素点的模值越小。为了进一步去除高频分量目标边缘提取结果中的噪声和伪边缘，本文根据上述性质，构造双层掩膜对初提取的模极大值点分别进行筛选。以首次结果为基础，综合第2次筛选结果，进行补充连接，最后将低频分量置零，经过逆变换得到高频分量目标边缘提取结果，避免了单层掩膜构造不合理导致的漏检和虚警问题。 2.2 基于改进数学形态学的低频分量目标边缘提取 传统的数学形态学边缘提取方法实质上是利用单个结构元素去探测图像中相对应的特征，通过调整该结构元素大小，提取出图像边缘，实现对图像的解译和分析[13]。由于低频分量中包含目标边缘的基本轮廓和部分细节信息，本文采用改进的数学形态学方法提取分解后的遥感图像低频分量目标边缘。 腐蚀运算和膨胀运算均能较好地保持原始图像的轮廓，其中腐蚀运算可以消除目标外部的孤立点，使目标缩小，而膨胀运算可以消除目标内部的孤立点，使目标增大，两者相减即可得到目标的粗略轮廓。对于灰度图像G，令S表示结构元素，,分别表示腐蚀和膨胀运算，在这两种运算的基础上，开操作和闭操作可分别由式(4)、(5)定义，据此剔除比结构元素更小的亮斑和暗斑，即 ()GSGSS (4) ()GSGSS (5) 形态学边缘检测算子一般由腐蚀、膨胀、开操作、闭操作组合而成。由于传统的形态学边缘检测算子对噪声异常敏感，而腐蚀和闭操作能有效减少负脉冲噪声的影响，膨胀和开操作则更适用于减少正脉冲噪声的影响，因此可对其进行改进 EGSSGSS (6) 其中，结构元素的选取对最终边缘提取结果的优劣有很大影响。式(6)采用单结构元素，运算简单，但不利于图像边缘细节的保持且抗噪性不强。为了进一步滤除噪声并提取图像中多方向的边缘，本文选取关于中心对称且互补的十字形和交叉形的结构元素S1, S2，如图4所示，提出一种互补型双结构元素的数学形态学方法，以此对遥感图像分解后的低频分量进行边缘提取 L1212EGSSGSS (7) (a) 结构元素S1 (b) 结构元素S2 图4 结构元素示意图
    第4期 吴诗婳，等：基于NSST和改进数学形态学的遥感图像目标边缘提取 527 利用结构元素S1对遥感图像经NSST分解后所得到的低频分量进行开操作和闭操作，再利用结构元素S2对低频分量进行膨胀和腐蚀操作，最终将两者相减，提取出低频分量的目标边缘。 2.3 方法具体步骤及流程图 本文提出的基于NSST模极大值和改进的双结构元素数学形态学的遥感图像目标边缘提取方法的流程图，如图5所示。 图5 基于NSST和改进数学形态学的目标边缘 提取流程图 本方法的步骤如下： 步骤1. 遥感图像NSST分解：①遥感图像多尺度分解。对遥感图像F，采用NSP进行j层(j=1, …, n)多尺度分解，得到低频分量及各个尺度下的高频分量。本文选取分解层数j=3，即得到一个低频分量lF和3个高频分量123,hhhFFF,；②高频分量多方向剖分。构建带方向和尺度变化的Meyer小波窗分别对多尺度分解后的高频分量123,hhhFFF,进行方向剖分，再对所得的一系列锥形方向分量进行坐标映射，最终得到各个方向子带的NSST系数。本文选取方向剖分级数l=3，即任意一个高频分量均有10个不同的方向子带1,hiF 2345678910(1,2,3),,,,,,,,hihihihihihihihihiiFFFFFFFFF。 步骤2. 高频分量边缘提取。通常高频分量中包含较丰富的边缘细节信息，因此根据式(3)对高频分量中的每个方向子带进行简便的模极大值检测，提取高频分量的目标边缘。为了去除边缘提取结果中的噪声以及伪边缘，构造双层掩膜对初提取的模极大值点进行筛选，经过反变换得到高频分量目标边缘提取结果HE。 步骤3. 低频分量边缘提取。通常低频分量中包含目标边缘的基本轮廓和部分细节信息，对于NSST分解后的低频分量lF，采用上述改进的双结构元素数学形态学方法，根据式(7)对低频分量进行目标边缘提取，得到低频分量目标边缘提取结果LE。 步骤4. 高、低频边缘提取结果融合。鉴于NSST具有平移不变性，为了充分利用NSST模极大值检测与数学形态学的优势，以加权的方式将高、低频分量的边缘提取结果进行融合，融合后边缘提取结果FHLabEEE(,0,ab1)ab。 步骤5. 区域连通性处理。依据区域连通性准则，进一步去除边缘提取结果FE中残留的孤立噪声点，由此得到最终的遥感图像目标边缘提取 结果。 3 实验结果与分析 现针对大量遥感图像进行边缘提取实验，以此验证本文提出的基于NSST模极大值和互补型双结构元素数学形态学的遥感图像目标边缘提取方法的性能，并将本文方法的实验结果与Canny[10]以及基于优化核的边缘滤波[14]、基于小波变换与边缘跟踪[15]、基于NSCT模极大值与Canny[17]、基于NSCT模极大值与数字形态学[21]等几种同类边缘检测算法进行对比，依据主观视觉效果及运行时间进行评价。选取其中4幅不同类型的遥感图像(海岸线、河岸、河流、建筑物)的目标边缘提取结果加以说明。图6~9中的(a)图分别为原始海岸线、河岸、河流、建筑物遥感图像，(b)~(e)图分别为采用Canny、基于小波与边缘跟踪、基于优化核的金字塔、基于NSCT模极大值与Canny、基于NSCT模极大值与数字形态学及本文等6种方法对这4幅遥感图像进行边缘提取的实验结果。 实验环境为Intel(R) Core(TM) i5 CPU 2.0 GHz、4 G RAM、Matlab R2013a。
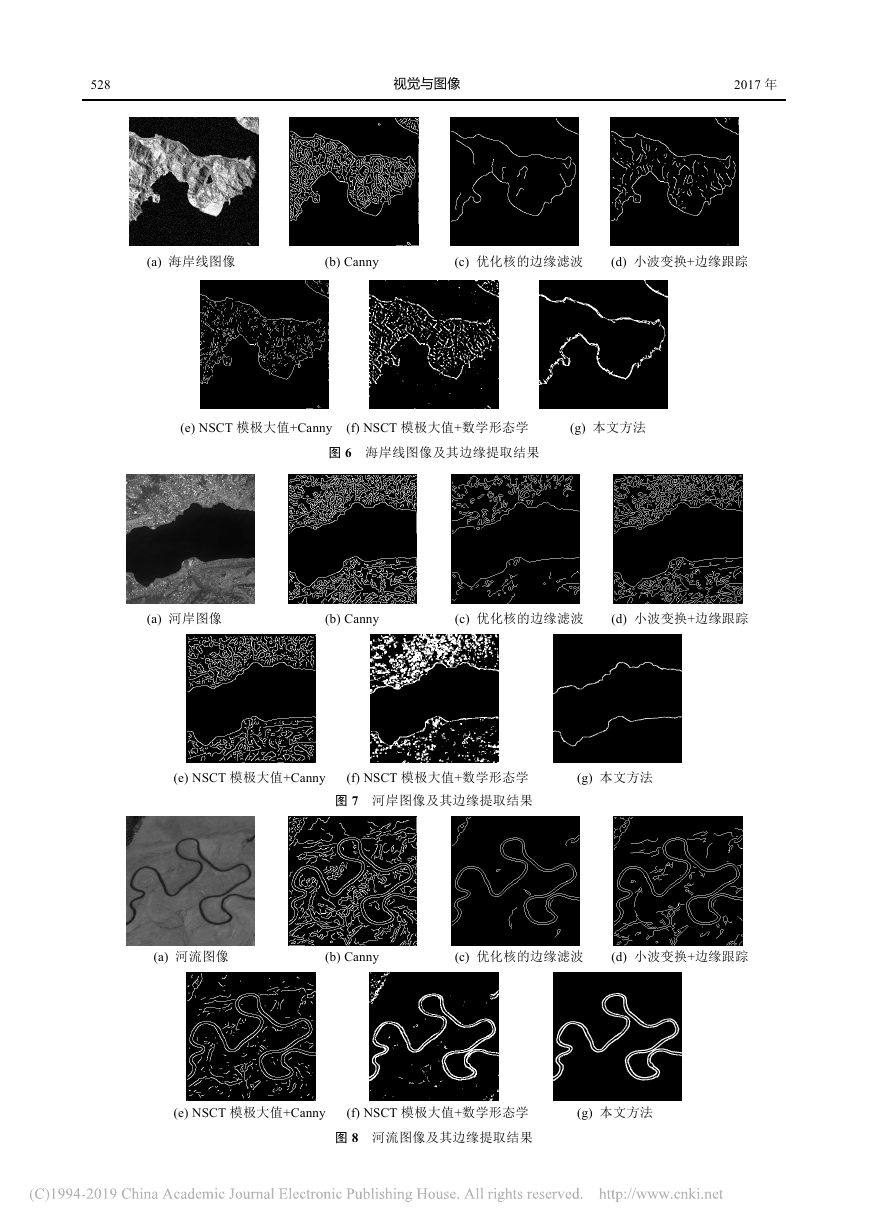
    528 视觉与图像 2017年 (a) 海岸线图像 (b) Canny (c) 优化核的边缘滤波 (d) 小波变换+边缘跟踪 (e) NSCT模极大值+Canny (f) NSCT模极大值+数学形态学 (g) 本文方法 图6 海岸线图像及其边缘提取结果 (a) 河岸图像 (b) Canny (c) 优化核的边缘滤波 (d) 小波变换+边缘跟踪 (e) NSCT模极大值+Canny (f) NSCT模极大值+数学形态学 (g) 本文方法 图7 河岸图像及其边缘提取结果 (a) 河流图像 (b) Canny (c) 优化核的边缘滤波 (d) 小波变换+边缘跟踪 (e) NSCT模极大值+Canny (f) NSCT模极大值+数学形态学 (g) 本文方法 图8 河流图像及其边缘提取结果
    第4期 吴诗婳，等：基于NSST和改进数学形态学的遥感图像目标边缘提取 529 (a) 建筑物图像 (b) Canny (c) 优化核的边缘滤波 (d) 小波变换+边缘跟踪 (e) NSCT模极大值+Canny (f) NSCT模极大值+数学形态学 (g) 本文方法 图9 建筑物图像及其边缘提取结果 对遥感图像进行目标边缘提取主要是为了获得目标的外部边缘轮廓，剔除背景及目标内部的伪边缘。其中海岸线图像(图6(a))的目标边缘细节丰富，目标内部纹理复杂、背景较平滑、有少许噪声；河岸图像(图7(a))的目标内部平滑、背景纹理复杂；河流(图8(a))与建筑物图像(图9(a))的目标形状相对细长、背景有部分纹理和噪声。从图6~9的(b)、(d)、(e)边缘提取结果中可以看出，Canny方法、基于小波变换与边缘跟踪方法、基于NSCT模极大值与Canny方法受图像中目标内部及背景的纹理、噪声影响较大，提取结果中存在大量的虚假边缘，不利于后续对遥感图像目标的分析与识别。基于优化核的边缘滤波方法、基于NSCT模极大值与数字形态学方法在一定程度上减少了背景和噪声的干扰，但仍存在少许伪边缘，所提取的目标边缘轮廓的间断点较多，粗糙且不连续。如图6(c)和(f)的右半部分，提取出的海岸线均存在断裂、残缺的现象，丢失了部分细节信息。图8(f)中，虽然可以检测出河流的基本边缘轮廓，但河流弯曲处的边缘模糊粗糙。对目标边缘间距窄的图像，由于提取出的边缘较粗，基于NSCT模极大值与Canny、基于NSCT模极大值与数字形态学这两种方法均易造成边缘重叠的情况，如图9(e)、(f)中条形建筑物目标信息湮灭，直接影响到后续的建筑物目标提取与识别。相比之下，本文方法提取出的目标边缘定位准确、轮廓清晰完整、连续性好、细节丰富。因此，从主观视觉效果来说，无论图像中目标内部、背景是否包含复杂的纹理、噪声，本文方法均可以在保持完整准确的目标轮廓边缘的同时，抑制伪边缘，具有更强的抗噪性。 为了进一步验证本文方法的准确性，以品质因数(figure of merit, FOM)[22]为依据对上述6种边缘提取方法进行定量评价，见表1。该指标通过比较6种方法所提取的目标边缘与人工标记的理想边缘之间的差异大小对提取结果进行评判，其值越接近1，表明所提取的目标边缘越准确，伪边缘越少。表1显示本文方法的边缘提取品质因数均高于其他5种方法。综上，在边缘提取效果方面，本文提出的基于NSST模极大值和互补型双结构元素数学形态学的遥感图像目标边缘提取方法无论在主观视觉效果，还是定量评价指标上，均具有明显的优越性。 表1 6种方法的边缘提取品质因数 边缘提取方法 海岸线 图像 河岸 图像 河流图像建筑物图像 Canny 0.579 5 0.594 3 0.594 10.549 0优化核的边缘滤波 0.843 1 0.860 4 0.886 30.899 3小波变换+边缘跟踪 0.813 3 0.602 1 0.653 90.795 5NSCT模极大值法+Canny 0.683 4 0.614 8 0.633 50.764 1NSCT模极大值+数学形态学0.779 5 0.838 1 0.874 10.845 5本文方法 0.873 4 0.924 1 0.915 30.923 9 基于上述对边缘提取效果的评价可知，Canny方法、基于小波变换与边缘跟踪方法、基于NSCT模极大值与Canny方法所得结果较差，不利于后续遥感图像的分割与描述、特征提取与分类识别。鉴于此，表2给出了优化核的边缘滤波方法、基于NSCT模极大值与数字形态学方法、本文方法的运行时间比较。从表中可以看出，本文方法的运行时间最快，与基于NSCT模极大值与数学形
    530 视觉与图像 2017年 态学方法相比，缩短了约35%。另外，在实际工程应用中可将高频分量与低频分量同时进行边缘提取，进一步提高方法的运行速度。 表2 3种方法的运行时间比较(s) 边缘提取方法 海岸线 图像 河岸 图像 河流图像建筑物图像 优化核的边缘滤波 2.732 1 2.314 3 3.019 93.321 0NSCT模极大值法+数学形态学 3.483 8 3.475 6 3.332 13.565 4本文方法 2.140 5 2.201 4 2.979 62.079 9 4 结 论 为了进一步改善遥感图像的目标边缘提取效果，本文提出了一种基于NSST模极大值和互补型双结构元素数学形态学的边缘提取方法。首先利用NSST对遥感图像进行多尺度、多方向分解，然后分别提取高频分量、低频分量的细节边缘以及轮廓边缘。一方面，鉴于高频分量中细节信息较为丰富，采用NSST模极大值算法对高频分量进行双层掩模筛选处理，抑制伪边缘，得到高频细节边缘。另一方面，采用改进的数学形态学方法对低频分量进行目标边缘提取，得到低频轮廓边缘，以中心对称互补型的双结构元素代替传统的单结构元素，使边缘提取结果更加准确。最后，对高频细节边缘和低频轮廓边缘进行加权融合，并利用区域连通性准则去除融合结果中残留的孤立噪声点，得到最终的目标边缘提取结果，进一步提高了本文方法的抗噪性。针对海岸线、河岸、河流、建筑物等不同类型遥感图像的实验结果表明，与Canny、基于优化核的边缘滤波、基于小波变换与边缘跟踪、基于NSCT模极大值与Canny、基于NSCT模极大值与数字形态学等5种边缘提取方法相比，本文方法具有明显的优势，能得到更好的边缘提取结果。利用本文方法提取的目标边缘轮廓更完整清晰、细节丰富、连续性好、并且具有更强的抗噪性、伪边缘少，是一种行之有效的遥感图像目标边缘提取方法。 参 考 文 献 [1] ZHANG R Q, ZHU D L. Study of land cover classification based on knowledge rules using high-resolution remote sensing images [J]. Expert System with Applications, 2011, 38(4): 3647-3652. [2] 黄秋燕, 肖鹏峰, 冯学智, 等. 结合相位一致与全变差模型的高分辨率遥感图像边缘检测[J]. 中国图象图形学报, 2014, 19(3): 439-446. [3] ZHANG T, YANG X M, HU S S, et al. Extraction of coastline in aquaculture coast from multispectral remote sensing images: object-based region growing integrating edge detection [J]. Remote Sensing, 2013, 5(9): 4470-4487. [4] 王珂, 肖鹏峰, 冯学智, 等. 基于频域滤波的高分辨率遥感图像城市河道信息提取[J]. 遥感学报, 2013, 17(2): 269-285. [5] HUANG X, ZHANG L P, LI P X. Classification of very high spatial resolution imagery based on the fusion of edge and multispectral information [J]. Photogrammetric Engineering and Remote Sensing, 2008, 74(12): 1585-1596. [6] 陆宗骐, 梁诚. 用Sobel算子细化边缘[J]. 中国图象图形学报, 2000, 5(6): 516-520. [7] 刘明艳, 赵景秀, 孙宁. 用Prewitt算子细化边缘[J]. 光电子技术, 2006, 26(4): 259-263. [8] 严国萍, 戴若愚, 潘晴, 等. 基于LOG算子的自适应图像边缘检测方法[J]. 华中科技大学学报: 自然科学版, 2008, 36(3): 85-87. [9] ZHOU P, YE W J, XIA Y J, et al. An improved Canny algorithm for edge detection [J]. Journal of Computational Information Systems, 2011, 75(5): 1516-1523. [10] MCILHAGGA W. The Canny edge detector revisited [J]. International Journal of Computer Vision, 2011, 91(3): 251-261. [11] LIU H, JEZEK K C. Automated extraction of coastline from satellite imagery by integrating Canny edge detection and locally adaptive thresholding methods [J]. International Journal of Remote Sensing, 2004, 25(5): 937-958. [12] 李辉, 代侦勇, 张利华, 等. 利用数学形态学的遥感影像水系提取方法[J]. 武汉大学学报: 信息科学版, 2011, 36(8): 956-959. [13] KAUR B, GARG A. Mathematical morphological edge detection for remote sensing images [C]//3rd International Conference on Future Computer and Communication (ICFCC 2011). New York: IEEE Press, 2011: 324-327. [14] WILSON R, BHALERAO A H. Kernel designs for efficient multiresolution edge detection and orientation estimation [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1992, 14(3): 384-390. [15] SHIH M Y, TSENG D C. A wavelet-based multiresolution edge detection and tracking [J]. Image and Vision Computing, 2005, 23(4): 441-451. [16] PO D D Y, DO M N. Directional multiscale modeling of images using the contourlet transform [J]. IEEE Transactions on Image Processing, 2006, 15(6): 1610-1620. [17] 肖易寒, 席志红, 海涛, 等. 基于非下采样contourlet变换的图像边缘检测新方法[J]. 系统工程与电子技术, 2011, 33(7): 1668-1672. [18] LI Q W, HOU G Y, LI H, et al. Bionic vision-based synthetic aperture radar image edge detection method in non-subsampled contourlet transform domain [J]. IET Radar Sonar and Navigation, 2012, 6(6): 526-535. [19] 侯彪, 胡育辉, 焦李成. SAR图像水域的改进Shearlet边缘检测[J]. 中国图象图形学报, 2010, 15(10): 1549-1554. [20] KARAMI A, HEYLEN R, SCHEUNDERS P. Band-specific shearlet-based hyperspectral image noise reduction [J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(9): 5054-5066. [21] HE K X, WANG Q, XIAO Y C, et al. Image edge detection based on nonsubsampled contourlet transform and mathematical morphology [J]. Journal of Southeast University (English Edition), 2012, 28(4): 445-450. [22] HEATH M D, SARKAR S. A robust visual method for assessing the relative performance of edge detection algorithms [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(12): 1338-1935.
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料