第1页 / 共21页
第2页 / 共21页
第3页 / 共21页
第4页 / 共21页
第5页 / 共21页
第6页 / 共21页
第7页 / 共21页
第8页 / 共21页
系统辨识参数辨识matlab程序.doc
一、考虑如下面的系统
( ) 0.8 ( -1)-0.15 ( -2)
y k
y k
y k
( -1) 0.5 ( -2)
u k
u k
( )
e k
分 别 取 (1)
1
)(
ke
4.01
1-
z
(k)e
~
)(
k
N(0,1);
(2)
)(
ke
(
）k
0.4
(k
-
1),
{ 为 白 噪 声 ； (3)
(k)}
。试采用伪随机信号作为输入，应用相关分析法辨识系统的
脉冲响应函数，并辨识出系统的模型参数。
要求：进行 Matlab 编程实现，程序功能应包括
(1) 实验数据的获取；
(2) 显示相关分析法辨识得到的 10 个脉冲响应结果；
(3) 在结构辨识的基础上进行参数辨识，结构的辨识算法自定；
(4) 不同参数辨识算法之间的比较，参数辨识算法应包括最小二乘算法；
(5) 对所估计的模型进行检验。
解：首先由系统方程多项式得系数矩阵：
1
(
A q
) ( )
y k
(
B q
1
) ( )
u k
( )
e k
其中，
1
(
A q
) 1 0.8
q
1
A
1
0.15
q
2
，
0.8 0.15
1
)
(
B q
q
，
B
1
0.5
q
2
0 1 0.5
，则系数矩阵为
。
输入信号采用伪随机二位式序列输入信号。
一、采用AR模型，噪声为 (k)~N(0,1)
法（遗忘因子取0.95）辨识系统的参数。
e
系统，分别采用最小二乘法和遗忘因子算
表1 用最小二乘法辨识参数
参数
真值
估值
1a
-0.8
-0.8348
表2 用遗忘因子法辨识参数
参数
真值
估值
1a
-0.8
-0.8537
2a
0.15
0.1676
2a
0.15
0.1999
用最小二乘法时的10个脉冲响应:
1b
1
1.026
1b
1
0.8961
2b
0.5
0.4361
2b
0.5
0.4983
-0.0337，0.9953，1.3087，0.8339，0.5033，0.2331，0.094，0.0764，0.00128，
0.0035。
用递推法时的10个脉冲响应:
0.032，0.9894，1.2508，0.8512，0.4925，0.3438，0.2348，0.1716，0.067，
0.0313。
1
0.5
0
-0.5
0
0.1
0.05
0
-0.05
-0.1
-25
1
0.5
0
-0.5
0
0.1
0
-0.1
-0.2
-0.3
-25
Correlation function of residuals. Output y1
5
10
lag
15
20
25
Cross corr. function between input u1 and residuals from output y1
-20
-15
-10
-5
0
lag
5
10
15
20
25
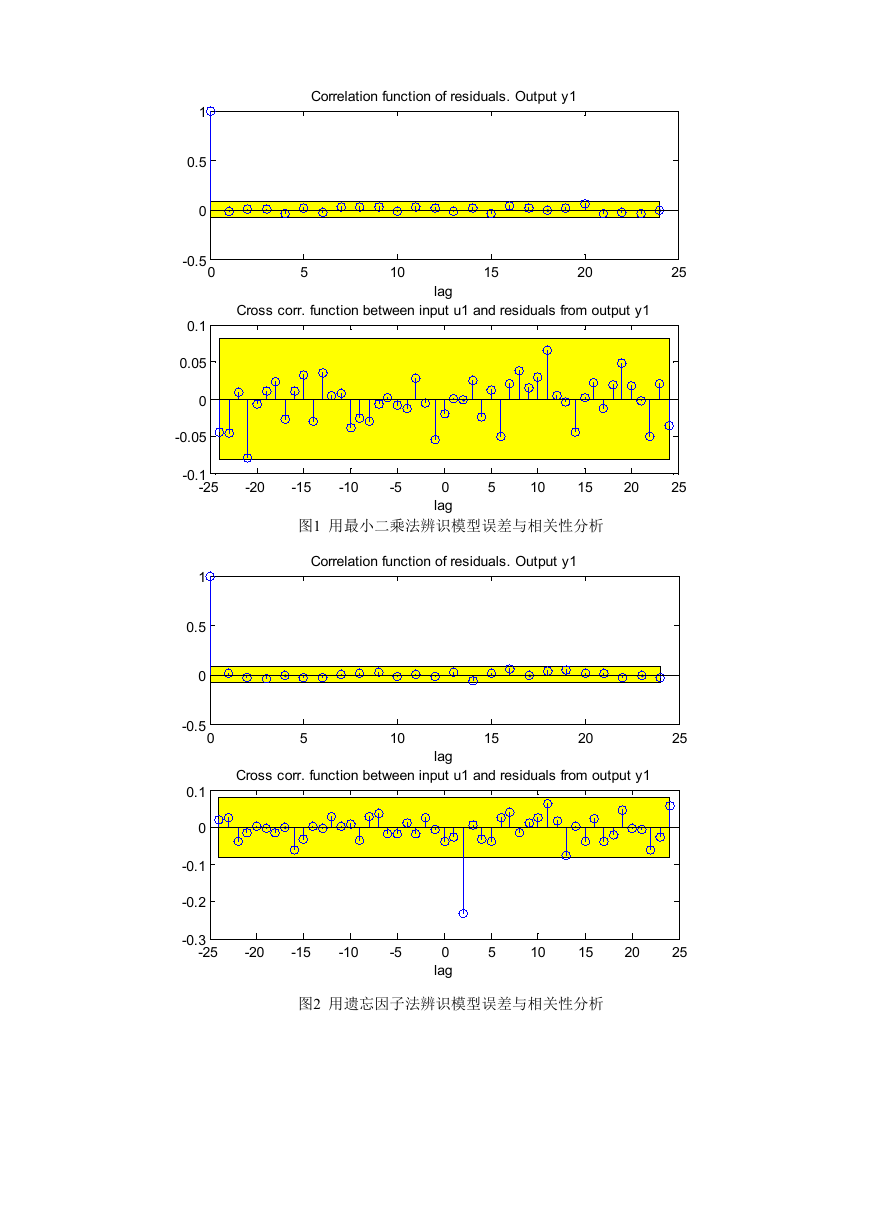
图1 用最小二乘法辨识模型误差与相关性分析
Correlation function of residuals. Output y1
5
10
lag
15
20
25
Cross corr. function between input u1 and residuals from output y1
-20
-15
-10
-5
0
lag
5
10
15
20
25
图2 用遗忘因子法辨识模型误差与相关性分析
二、采用ARMA模型，噪声为 ( )
e k
(
k
）
0.4 (k-1)
分别采用最小二乘法和遗忘因
子算法（遗忘因子取0.95）辨识系统的参数。
表3 用最小二乘法辨识参数
参数
真值
估值
1a
-0.8
-0.8296
表4 用遗忘因子法辨识参数
参数
真值
估值
1a
-0.8
-0.9191
2a
0.15
0.162
2a
0.15
0.2500
最小二乘法10个脉冲响应：
1b
1
2b
0.5
c
0.4
1.073
0.5017
0.3581
1b
1
2b
0.5
c
0.4
1.1019
0.4916
0.3621
0.009，0.9825，1.2818，0.8841，0.5405，0.3737，0.2341，0.0938，0.0848，
0.0999。
遗忘因子法10个脉冲响应：
0.0291。
-0.0673，0.9917，1.3205，0.8855，0.4718，0.2276，0.1026，0.0465，0.043，
1
0.5
0
-0.5
0
0.2
0.1
0
-0.1
-0.2
-25
Correlation function of residuals. Output y1
5
10
lag
15
20
25
Cross corr. function between input u1 and residuals from output y1
-20
-15
-10
-5
0
lag
5
10
15
20
25
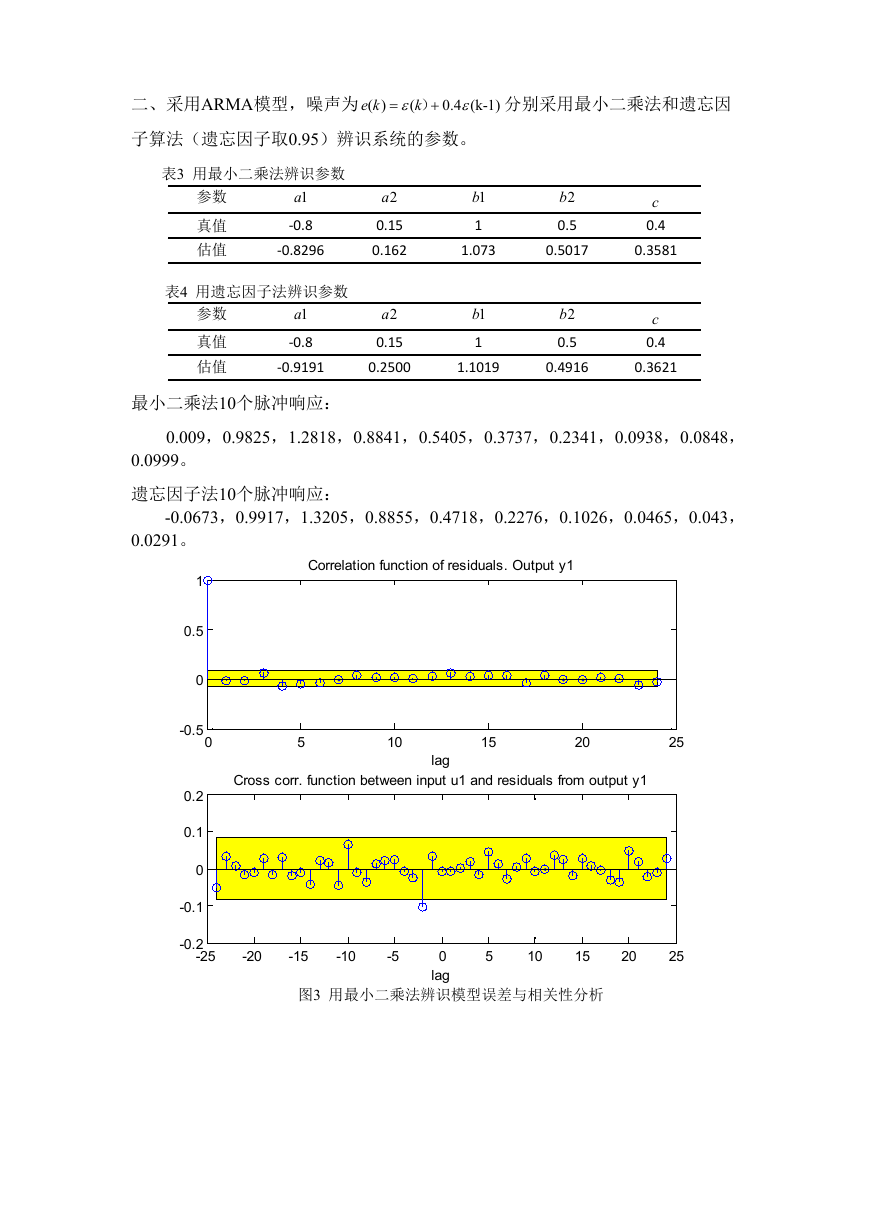
图3 用最小二乘法辨识模型误差与相关性分析
1
0.5
0
-0.5
0
0.4
0.2
0
-0.2
-0.4
-25
Correlation function of residuals. Output y1
5
10
lag
15
20
25
Cross corr. function between input u1 and residuals from output y1
-20
-15
-10
-5
0
lag
5
10
15
20
25
图4 用遗忘因子法法辨识模型误差与相关性分析
(3)采用DA模型，噪声为
)(
ke
1-
法（遗忘因子取0.95）辨识系统的参数。
z
1
4.01
)(
k
，别采用最小二乘法和遗忘因子算
表5 用最小二乘法辨识参数
参数
真值
估值
1a
-0.8
-0.8242
表6 用遗忘因子法辨识参数
参数
真值
估值
1a
-0.8
-0.6461
2a
0.15
0.1737
2a
0.15
0.1354
最小二乘法10个脉冲响应：
1b
1
2b
0.5
c
0.4
1.002
0.4241
0.3992
1b
1
2b
0.5
c
0.4
0.951
0.8705
0.3263
-0.0314，0.9673，1.2975，0.9164，0.5205，0.2598，0.1514，0.0989，0.021，
0.0001。
遗忘因子法10个脉冲响应：
-0.1049，0.9483，1.236,4，0.8119，0.5007，0.3232，0.1646，0.0362，-0.0228，
0.04。
Correlation function of residuals. Output y1
5
10
lag
15
20
25
Cross corr. function between input u1 and residuals from output y1
-20
-15
-10
-5
0
lag
5
10
15
20
25
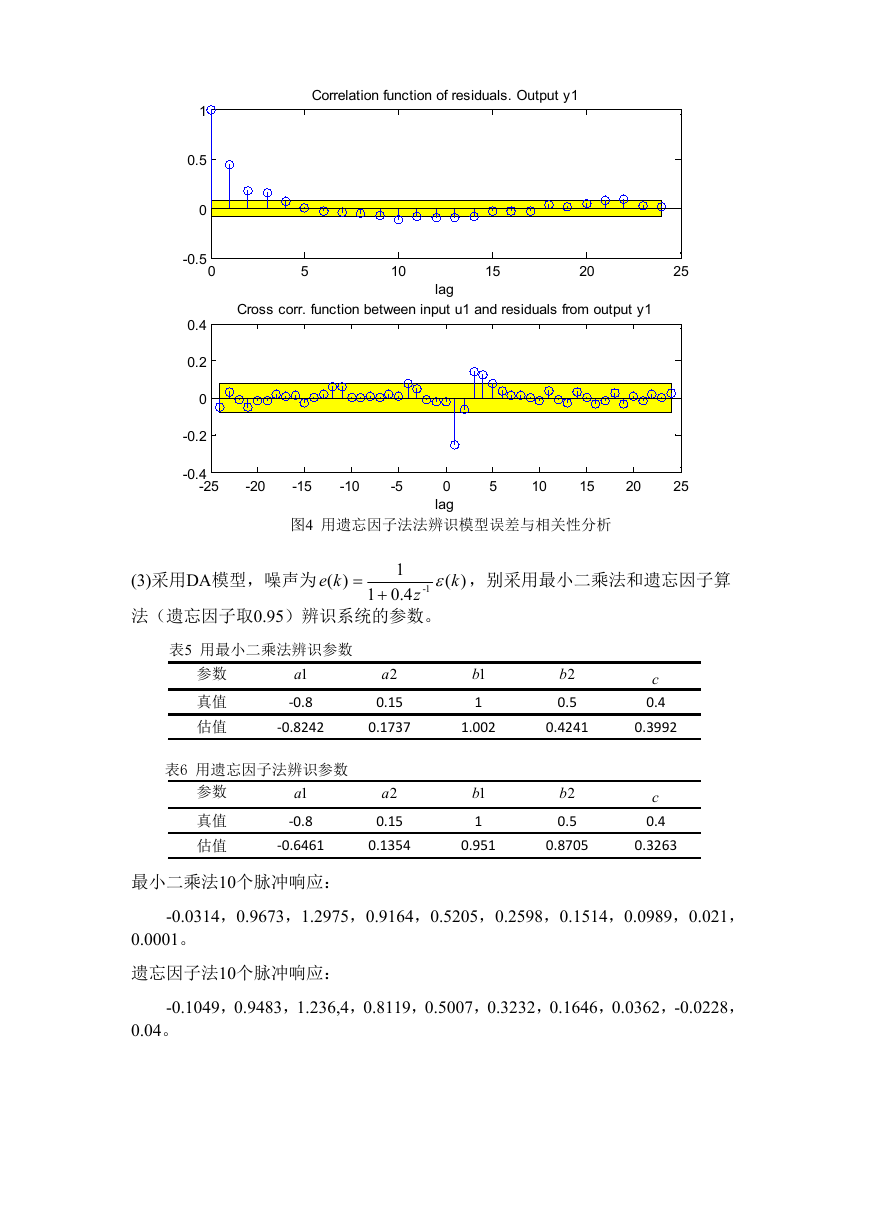
图5 用最小二乘法辨识模型误差与相关性分析
Correlation function of residuals. Output y1
5
10
lag
15
20
25
Cross corr. function between input u1 and residuals from output y1
1
0.5
0
-0.5
0
0.1
0.05
0
-0.05
-0.1
-25
1
0.5
0
-0.5
0
0.3
0.2
0.1
0
-0.1
-25
-20
-15
-10
-5
5
10
15
20
25
0
lag
图6 用遗忘因子法法辨识模型误差与相关性分析
仿真程序见程序1。
二、利用 BP 网络拟合非线性函数
)(
tY
e
201.0
t
cos
1.1
)2(
t
要求：进行 Matlab 编程实现，程序功能应包括
(1) 利用 Simulink 工具箱来实现系统数据的生成，输出数据直接导入 matlab 的
workpace 中；
(2) 给出不同隐含层的 BP 网络拟合结果比较图
(3) 最大训练步数 1000 步，目标函数误差
1
-310
解：训练算法选取比例共轭梯度算法(trainscg),隐含层结点数分别取 15 和 40
个进行比较。
由 Simulink 生成的仿真框图如下：
Repeating
Sequence
示波器端输出信号波形为
p{1}
y {1}
Neural Network
y{1}
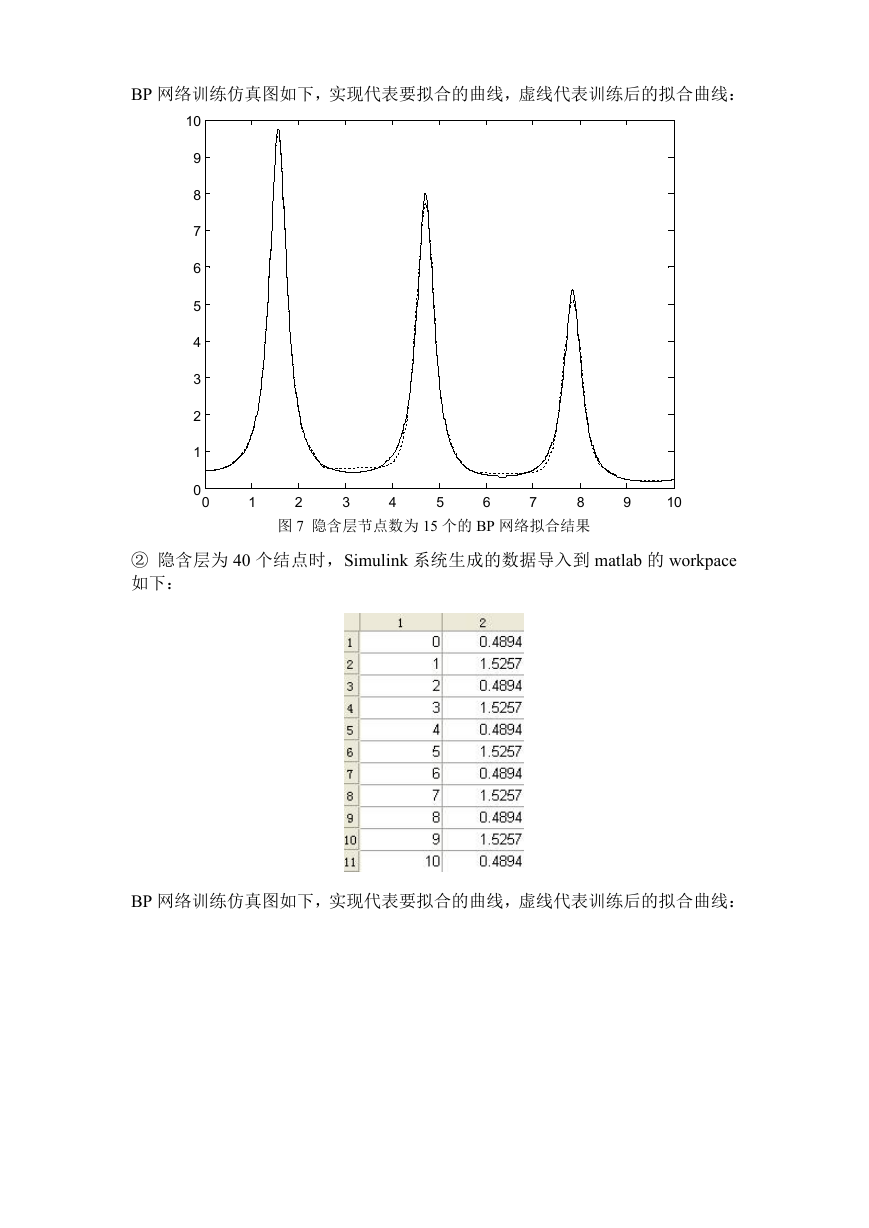
① 隐含层为 15 个结点时，Simulink 系统生成的数据导入到 matlab 的 workpace
如下：
BP 网络训练仿真图如下，实现代表要拟合的曲线，虚线代表训练后的拟合曲线：
10
9
8
7
6
5
4
3
2
1
0
0
1
3
2
8
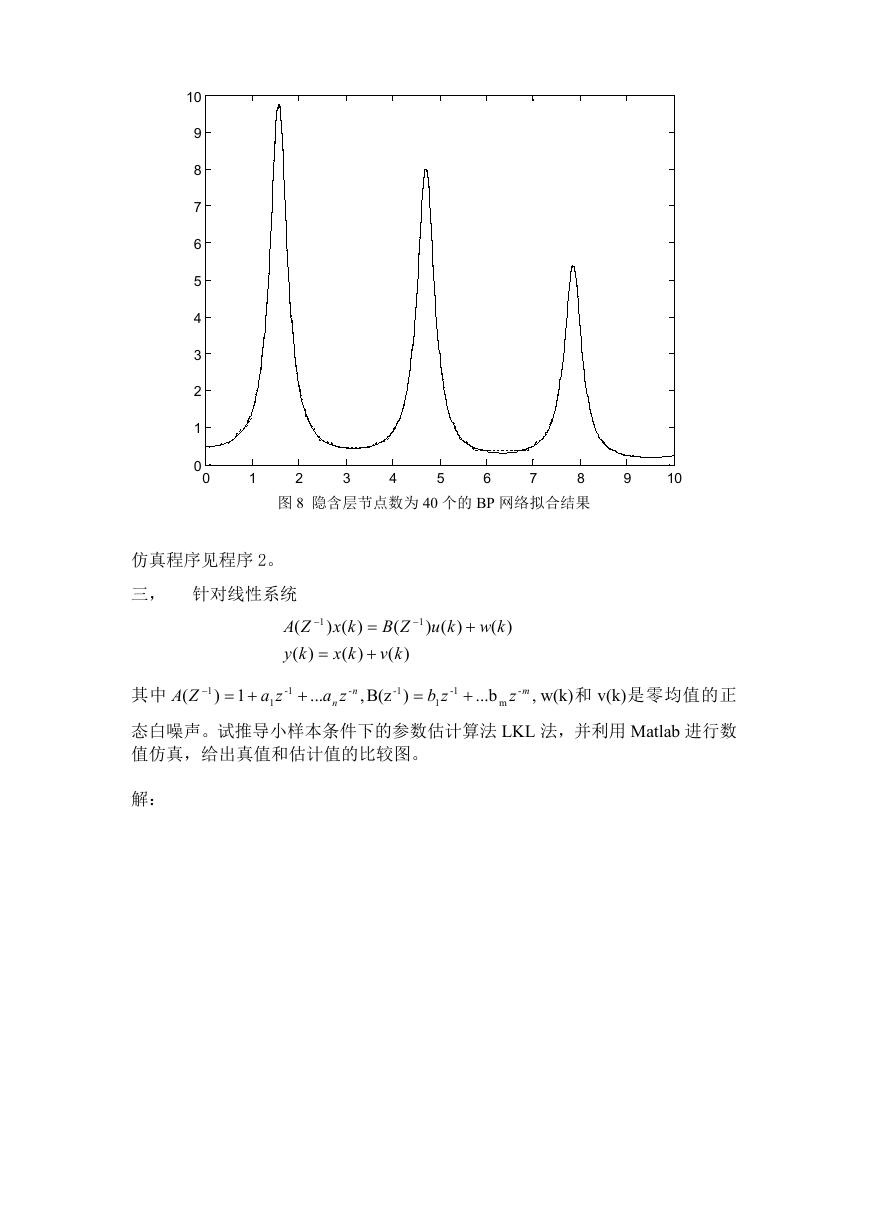
图 7 隐含层节点数为 15 个的 BP 网络拟合结果
4
5
6
7
9
10
② 隐含层为 40 个结点时，Simulink 系统生成的数据导入到 matlab 的 workpace
如下：
BP 网络训练仿真图如下，实现代表要拟合的曲线，虚线代表训练后的拟合曲线：
10
9
8
7
6
5
4
3
2
1
0
0
1
3
2
8
图 8 隐含层节点数为 40 个的 BP 网络拟合结果
4
5
6
7
9
10
仿真程序见程序 2。
三， 针对线性系统
(
ZA
)(
ky
1
)()
kx
)(
kx
1
)()
ku
)(
kw
(
ZB
)(
kv
其中
(
ZA
1
1)
1-
za
1
...
za
n
-
n
,
B(z
-1
)
1-
zb
1
...b
m
-
m
z
,
w(k)和 v(k)是零均值的正
态白噪声。试推导小样本条件下的参数估计算法 LKL 法，并利用 Matlab 进行数
值仿真，给出真值和估计值的比较图。
解：
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
