清华信号考研秘籍.pdf-资料库

5d1b01c3-f64d-4fde-8aa5-7c51ba618fbf.pdf-第1页.png

第1页 / 共64页

5d1b01c3-f64d-4fde-8aa5-7c51ba618fbf.pdf-第2页.png

第2页 / 共64页

5d1b01c3-f64d-4fde-8aa5-7c51ba618fbf.pdf-第3页.png

第3页 / 共64页

5d1b01c3-f64d-4fde-8aa5-7c51ba618fbf.pdf-第4页.png

第4页 / 共64页

5d1b01c3-f64d-4fde-8aa5-7c51ba618fbf.pdf-第5页.png

第5页 / 共64页

5d1b01c3-f64d-4fde-8aa5-7c51ba618fbf.pdf-第6页.png

第6页 / 共64页

5d1b01c3-f64d-4fde-8aa5-7c51ba618fbf.pdf-第7页.png

第7页 / 共64页

5d1b01c3-f64d-4fde-8aa5-7c51ba618fbf.pdf-第8页.png

第8页 / 共64页

Powered by BUAA yunan QQ：370531755 清华电子系考研《信号与系统》秘笈（V0.9）（请勿用于商业用途）参考资料：清华 2000~2010 信号考研真题陆建华《信号与系统》课件山秀明《信号与系统》讲义郑君里《信号与系统》（第二版）程佩青《数字信号处理教程》（第三版）注意：1.往年试题有一定的复现率，一定要认真对待。 2.考试时，在时间允许的情况下，解答应该尽量详细和严谨。基本计算题：冲激函数与冲激偶（00）1. （00）2. 积。其中，为连续有界函数，。其中，为连续有界函数，表示卷（01）（1）计算为冲激函数。的根为故。（01）（2）计算为冲激偶。解：1、直接法：利用P79页冲激函数性质（2-89）， 2、间接法：（08） 2.3 （10）1. 求，其中具有连续各阶导数。 1 (0)()()ftftdt()ft(,),0t00()()()tfttftt()ft(,),t(sin)?x()()cos0fttntn1(sin)()()cosnnnxxnxntsin()?xx()()()(0)()(0)()fttftftsin0()cos0()()xxxsin()cos()sin()xxxxxxsin()0()0sin()0xxxxxsin()0cos()()xxxxx()()?ttt()0()1()0ttt(3)()()fxx()fx333(3)()30(1)(0)(1)()kkkkkfxxCfx

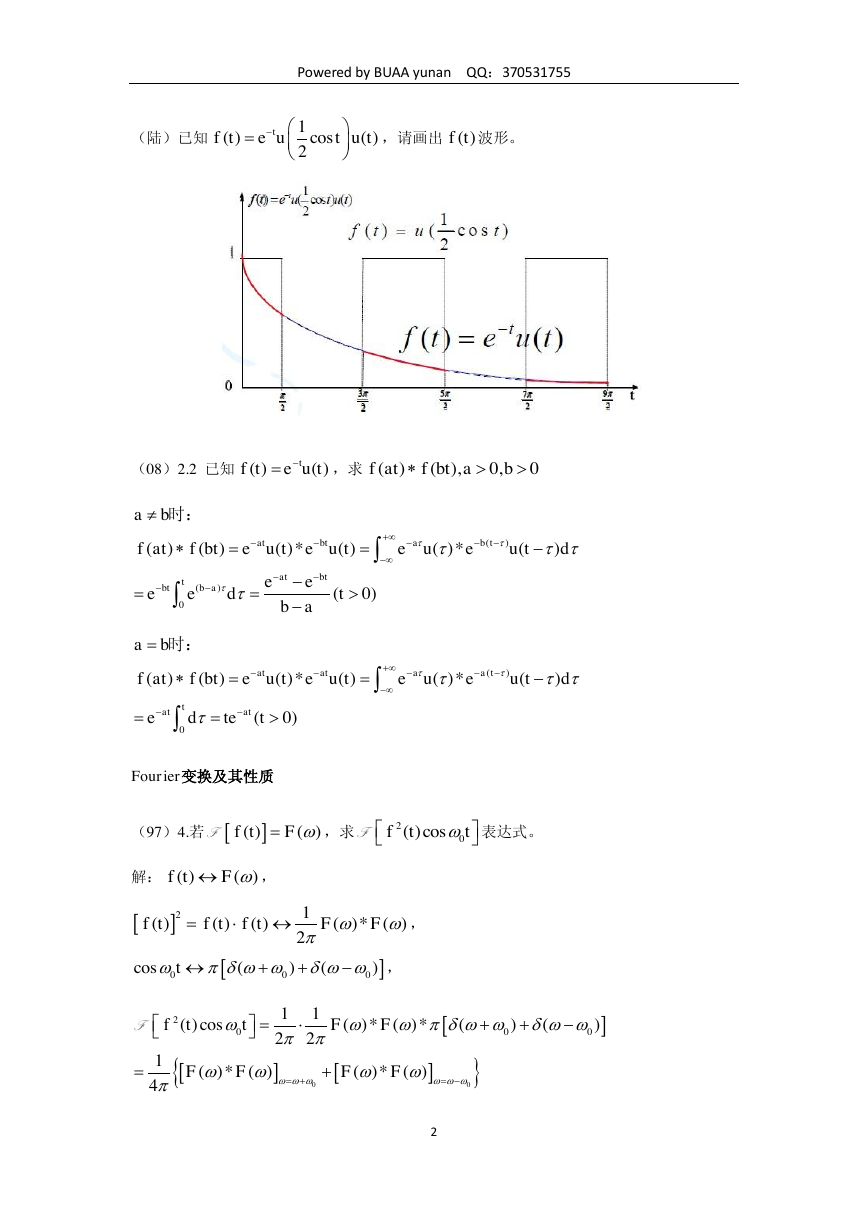
Powered by BUAA yunan QQ：370531755 （陆）已知，请画出波形。（08）2.2 已知，求 Fourier变换及其性质（97）4.若，求表达式。解：，，， 2 1()cos()2tfteutut()ft()()tfteut()(),0,0fatfbtab()()0()()()*()()*()(0)atbtabtatbttbtbaabfatfbteuteuteueutdeeeedtba时：()0()()()*()()*()(0)atataattatatabfatfbteuteuteueutdedtet时：()()ftFF20()cosfttF()()ftF21()()()()*()2ftftftFF000cos()()t00200011()cos()*()*()()221()*()()*()4fttFFFFFFF

Powered by BUAA yunan QQ：370531755 （07）2.求已调制电视测试信号的Fourier变换，其中，，和均为常数。解：根据Fourier变换对：，结合卷积定理计算可得：（07）3.已知的Fourier变换为，求的Fourier变换。解：，，注意积分性质与微分性质的区别，并不是简单的逆运算。（10）5.已知，求，其中。解：，，。（00）3. 的 Fourier 反变换。解：（陆）频谱函数的原函数 3 ()ft()F()1()1cos2cftAmutftAcfm1()()utjF=cos()()ccctF222(2)()(2)(2)42cccjAmAmFfff1()ft1()F12(1)tfd2()F11()()ftF111(2)()22ftF111(2(1))()22jftFe111(2)2(1)(0)()22jtFefdFj22etfeF2()?tetF01()()fatFaaF()()dftjFdtF222()()()[]tffeeeF2223()()()22tffejejfetF()f1()fF12211()()()jftjftffedffedfF()2(12)Fju()?ft

Powered by BUAA yunan QQ：370531755 Laplace 变换及其性质（00）4. 的 Laplace 变换请标明收敛域。（07）1.已知系统冲激响应，在零状态下输入信号，求：（1）系统输出并画出的波形。（2）输出的 Laplace 变换。解：（1）已知输入信号，根据卷积定理可得：（2）根据 Laplace 变换定义可得：最后一步的等比级数求和将决定 ROC 的范围，显然公比的模应小于 1，即注意：对于 Laplace 变换和 z 变换，讨论 ROC 都是必要的。（00）5. 的 Laplace 逆变换（01）（4）计算解： 4 112211()(),()2()111()(),2(2)()2211122()()2jtjtuttujjtututjjttutjetjett()2tt22()21(Re0)ttssL()()(1)htutut30(1)()ntntne()?yt()yt()yt30(1)()ntntne30()()*()()()(1)nnytxthteutnutn1300(3)(3)0()()()11()(1)(1)nstnstnnssnssnytytedteedteeesesL(3)se(3)1Re3ses441s111441()4114teutssLL321597?(1)(2)sssssL32112597212()2()(2)()(1)(2)12ttsssstteeutssssLL

Powered by BUAA yunan QQ：370531755 （07）4.求的Laplace逆变换。解：利用分步展开法可将化为：根据上式可得其逆变换为：（08）求的 Laplace 逆变换。解：（09）1.求的自相关函数。（参考：郑（上）P348）解：（00）6.序列的 z 变换请注明收敛域。（00）7.已知，求（01）（5）已知：，求解：极点1对应因果序列，极点2对应反因果序列，则由， 5 2322ssess2322sss222312cos2sin22(1)1(1)1ttssetetssssL1123(cos(1)2sin(1))(1)22stseettutssL223322sssess2223311()cos2222tsssttessss21233(1)cos(1)(1)22stssetteutss3sin4t22221()limsin()sin(())1limcos()cos(22)21cos2TTTTTTRttdtTtdtT(2)n2(2)(0)nzzZ()1Xz()()xnn2(),12(1)(2)zXzzzz()?xn22()(1)(2)21(1)zzzzXzzzzzz()2(1)()()nxnununnun

Powered by BUAA yunan QQ：370531755 （05）二、5.一个离散系统的冲激响应，请通过计算说明该系统为广义线性相位系统。解：，所以相位为广义线性。（09）3.把非最小相移系统用全通函数与最小相移函数表示，分别写出二者系统函数。解：（00）8.已知解：，其中是全通系统，是最小相位系统。。求的 DFT，即？（05）二、7.已知，求解：直接求特征值，可得到有两重特征根0。设，则：故可得（06）10.若，计算。解：直接求特征值，可得到有两重特征根。设，则：故可得： 6 ()8()8(2)hnnn2()8(1)Hzz()22()8(1)16sin16sinjjjjHeejee()21.50.5zz21.51.5320.50.53zzzzzz1.523zz230.5zz1212()()(),0xnnnnnnnN()xn()Xk12122210()(),0,1,2,,1NjknjknknknknNNNNNnDFTxnxnWWWeekN0010A?AteA01AtecIcA0000111ceccttec101AteItAt10AAteA01AtecIcA01011ttttteccceteteccte101()0100ttAttttteteeetetee

Powered by BUAA yunan QQ：370531755 概念是非题：（00）9.（√）由已知信号构造信号：，则为周期信号。（05）3.（√）因为 ,所以（陆）2.（×）奇函数与奇函数的卷积是奇函数。分析：如果是判断题，只需举出一反例即可；如果是证明题，则需要严格证明。、均为奇函数，而为偶函数，所以命题错误。（陆）3.（√）设系统的输入为，输出为，则该系统是时变因果系统。判断因果系统：现在的响应是否等于现在的激励＋以前的激励判断线性系统：先线性运算，再经系统是否等于先经系统，再线性运算判断时不变系统：时移，再经系统是否等于先经系统，再时移（陆）4.（）已知系统微分方程为，，，，则此系统的各起始条件在起始点都没有发生跳变。（00）2.（√）一个系统，对输入信号的运算规则为，是已知函数，则系统T必为线性系统。（10）6. 一个系统的输出与输入的零状态条件下的关系为：，式中是和的连续函数，请回答，该系统是线性系统吗？为什么？是（00,05）3.（×）非线性系统的全响应必等于零状态响应与零输入响应之和。（00）5.（√）周期信号的Fourier级数必处处收敛。（陆）1.（√）实周期信号的指数形式Fourier级数的系数，具有性质：，其中和分别为信号余弦分量和正弦分量的幅度。分析：由P91，利用是的偶函数，是的奇函数的性质。由于， 7 ()ft()()nFtftnT()Ft)()('ttdtd)()('tdt()t3()ftt2()()()3tftftt()xt2()(1)tytext222()3()4()()dddrtrtrtetdtdtdt(0)1r(0)1r()()etutT()ft()(,)()TftKxtftdt(,)Kxt()yt()xt(),ytktxd+(,)ktt2nnnajbFnnFFnanbnannbn00112()costTntafttdtT00112()sintTntbfttdtT

Powered by BUAA yunan QQ：370531755 ，。（陆）5.（×）与构成Fourier变换对。分析：由于是判断题，所以只需检验特殊点。针对此题，我们检验0点，为非负信号，必有直流，而题给频谱0点却为0值，由此发现矛盾，所以命题不正确。（00）10.（×）线性定常系统的频率响应一定等于系统冲激响应的Fourier变换。（05）9.（√）系统函数，系统输入，则系统的零状态响应为注：Laplace 变换默认为单边的。（陆）6.（×）的 Laplace 变换为，若，则。解答：如果使用终值定理，可得：是否正确？分析：特别注意终值定理的应用条件：仅当在平面的虚轴上及其右边都为解析时，终值定理才可应用。而题中在右平面上有两个不解析点，为振荡波形。（00）1. （×）一个全通系统与一个最小相位系统级联所组成的新系统必是最小相位的。（00）8. （×）全通系统必为无失真传输系统。分析：相频特性会改变。（05）2. （×）全通系统物理不可实现。（05）4. （√）两个最小相位信号的线性组合必是最小相位信号。（05）5. （×）理想低通滤波器必是线性相位滤波器。（05）6. （√）理想低通滤波器必不是 BIBO 稳定系统。（05）7. （√）理想低通滤波器物理上不可实现。（00）4. （√）复变信号的Hilbert变换无定义。（05）1. （√）Hilbert 变换对于不含直流分量的稳定信号构成全通系统。（05）8. （√）离散线性时不变系统的系统函数为，若和在单位圆上和单位圆外解析，则系统是严格最小相位的。（00）7. （×）两个有限序列的圆卷积（循环卷积）必等于它们的线卷积。（00）6. （×）和均为方阵，则必有。 8 ,nnnnaabb22nnnnnnajbajbFF3,1()0,X其他3sin()txtt()xt))()(()(321pspspsAsH()()()xtxtut312()[()]()ptptptytAeeextut()ft()Fs51()Fsss()lim11ttfte0lim()lim()tsftsFs400()1limlim()lim111ttssftsFses()sFss()sFs()ft()Hz()Hz1()HzABnn()ABtAtBteee

资料库

清华信号考研秘籍.pdf

相关推荐

考试认证

热门标签

最新资料