jbb0523（彬彬有礼）理论笔记系列文档 数字序列补零后引起的频谱变化 作者：jbb0523(彬彬有礼) DFT，全称 Discrete Fourier Transformation，中文译称离散傅里叶变换。 首先列出长度为 N 的数字序列 ( ) x n 的 DFT 公式： X k ( )  DFT x n [ ( )]      N 1  x n W ( ) kn N  n  0, 0 其它 ,0   k N  1 (1)  NW e 2j  N 。 上式中， 我们知道，对于一个数字序列来说，对其进行补零再求 DFT 可以得到它的高密度谱， 这样可以有效的去除栅栏效应等等。下面要讨论一个问题： 对数字序列 ( ) x n 分别进行前端补零、后端补零和前端后端同时补零，那么得到的三种 序列的频谱有什么区别？我们为了得到高密度谱，一般对序列进行后端补零，那么您想过没 有：前端补零会改变信号的频谱么？前端和后端同时补零会改变信号的频谱么？ 下面首先看一段程序。 clc; clear; N = 20; xn = randn(1,20); xn_f = [zeros(1,80) xn];%Front zero padding xn_e = [xn zeros(1,80)];%End zero padding xn_b = [zeros(1,20) xn zeros(1,60)];%Both front and end zero padding Xk = fft(xn);%求 xn 的频谱 Xk_f = fft(xn_f);%求 xn 前端补零的频谱 Xk_e = fft(xn_e);%求 xn 后端补零的频谱 Xk_b = fft(xn_b);%求 xn 两边同时补零的频谱 %Amplitude Am_Xk = abs(Xk); Am_Xk_f = abs(Xk_f); Am_Xk_e = abs(Xk_e); Am_Xk_b = abs(Xk_b); %Phase Ph_Xk = atan(imag(Xk)./real(Xk)); Ph_Xk_f = atan(imag(Xk_f)./real(Xk_f)); Ph_Xk_e = atan(imag(Xk_e)./real(Xk_e)); Ph_Xk_b = atan(imag(Xk_b)./real(Xk_b)); 第 1 页  

jbb0523（彬彬有礼）理论笔记系列文档 %绘图 figure(1); subplot(2,2,1); plot(Am_Xk,'LineWidth',2,'color','r');grid;title('Xk Amplitude'); subplot(2,2,2); plot(Am_Xk_f,'LineWidth',2,'color','r');grid;title('Xk Front Amplitude'); subplot(2,2,3); plot(Am_Xk_e,'LineWidth',2,'color','r');grid;title('Xk End Amplitude'); subplot(2,2,4); plot(Am_Xk_b,'LineWidth',2,'color','r');grid;title('Xk Both Amplitude'); figure(2); subplot(2,2,1); plot(Ph_Xk,'LineWidth',2,'color','r');grid;title('Xk Phase'); subplot(2,2,2); plot(Ph_Xk_f,'LineWidth',2,'color','r');grid;title('Xk Front Phase'); subplot(2,2,3); plot(Ph_Xk_e,'LineWidth',2,'color','r');grid;title('Xk End Phase'); subplot(2,2,4); plot(Ph_Xk_b,'LineWidth',2,'color','r');grid;title('Xk Both Phase'); 在 Matlab 中运行以上程序，得到以下两幅图。（由于并不关心究竟是什么数字序列，此 处随机生成，因此每次运行的结果会有所不同） 图 1 figure(1)幅度谱 第 2 页    

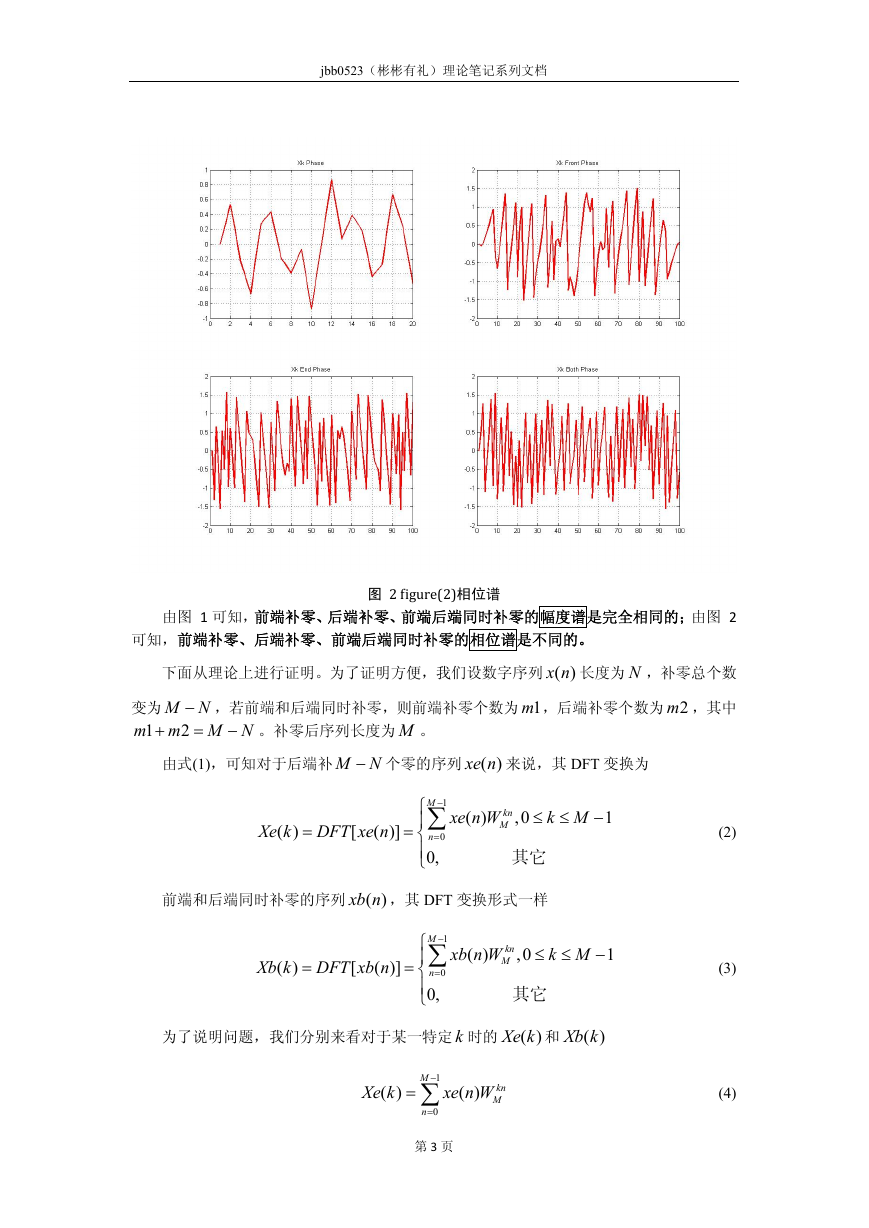
jbb0523（彬彬有礼）理论笔记系列文档 图 2 figure(2)相位谱   由图  1 可知，前端补零、后端补零、前端后端同时补零的幅度谱是完全相同的；由图  2 可知，前端补零、后端补零、前端后端同时补零的相位谱是不同的。 下面从理论上进行证明。为了证明方便，我们设数字序列 ( ) x n 长度为 N ，补零总个数 变为 M N ，若前端和后端同时补零，则前端补零个数为 1m ，后端补零个数为 2m ，其中 m m M N 1  。补零后序列长度为 M 。 2   由式(1)，可知对于后端补 M N 个零的序列 ( ) xe n 来说，其 DFT 变换为 Xe k ( )  DFT xe n ( )] [      M 1  ( ) xe n W kn M  n  0, 0 其它 ,0   k M  1 前端和后端同时补零的序列 ( ) xb n ，其 DFT 变换形式一样 Xb k ( )  DFT xb n ( )] [      M 1  ( ) xb n W kn M  n  0, 0 其它 ,0   k M  1 为了说明问题，我们分别来看对于某一特定 k 时的 ( ) Xe k 和 ( ) Xb k Xe k ( ) M 1    n  0 xe n W kn M ( ) 第 3 页  (2) (3) (4) 

jbb0523（彬彬有礼）理论笔记系列文档 Xb k ( ) M 1    n  0 xb n W kn M ( ) 对于 ( ) xe n 来说，其后 M N 个 ( ) xe n 值为零，因此式(4)可另写为 Xe k ( ) N 1    n  0 xe n W kn M ( ) 对于 ( ) xb n 来说，其前 1m 和后 2m 个值为别为零，因此式(5)可另写为 Xb k ( ) 2 1  M m    n m 1  xb n W kn M ( ) 对式(7)进行变形，提出公因式 1km MW ，整理得 Xb k W km 1 M ( )    W km 1 M  N 1   n  0 M m m   2 1 1   n  0 xb n m W kn M 1)  ( xb n m W kn M 1)  ( (5) (6) (7) (8) 对于序列 ( ) xe n 来说，其 (0) ~ xe xe N  即原始数字序列 ( )x n ；对于序列 ( ) xb n 来 1) ( 说，其 ( 1) ~ xb m xb m N ( 1  也是原始数字序列 ( )x n ，因此式(6)和式(8)分别可以表示成 1) 式(9)和式(10)。 Xe k ( ) N 1    n  0 x n W ( ) kn M Xb k W km 1 M ( )  N 1   n  0 x n W ( ) kn M (9) (10) 比较式(9)和式(10)可以发现，二者仅相差一个系数 1km MW ，而此系数取模后其值为 1， 因此将数字序列 ( )x n 后端补零和两端分别补零至同一长度 M 时，其幅度谱是相同的，相位 谱由于 1km MW 的存在而存在差异。对于仅前端补零所得序列来说，与两端补零所得序列的差 别仅在于提取的公因式系数不同，可以得到相同的结论。 到此，前述问题，得证！ 第 4 页