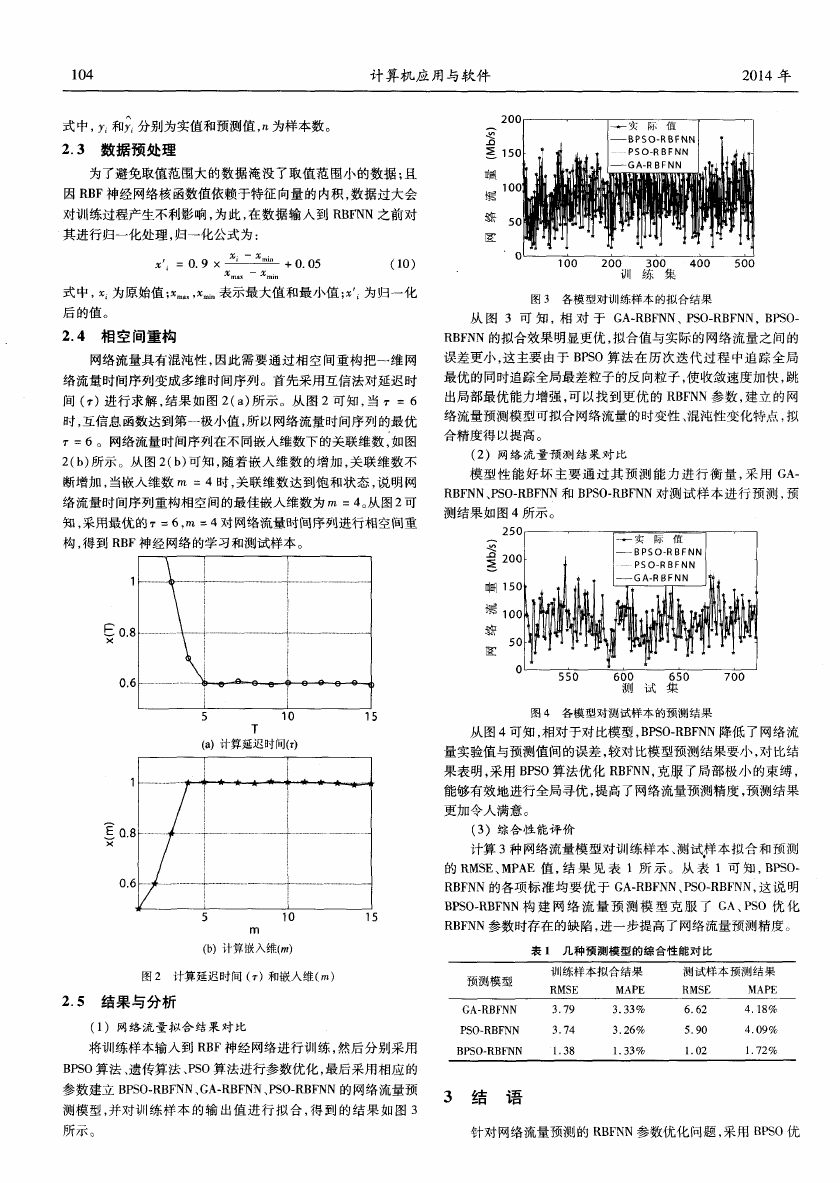
104 计 算机 应 用与软件 2014．缸 式 中，y 和y 分别 为实值和 预测值 ， 为样本数 。 2．3 数 据预 处理 为 了避免取值范 围大 的数据淹 没了取值 范 围小 的数据 ；且 因 RBF神经网络核 函数值依赖于特征 向量 的内积 ，数 据过大会 对训练过程产生不利影响 ，为此 ，在数 据输入 到 RBFNN之前对 其 进 行 归 一 化 处 理 ，归 一 化 公 式 为 ： = 0．9 × — 二 + 0 ． 05 … 一 m i“ (10) 式 中 ， 为原始值 ；x… ， … 表示最大值 和最 小值 ； 为归一化 后 的值 。 2．4 相 空 间重构 网络流量具有混沌性 ，因此 需要通过 相空 间重构把一 维 网 2O0 D 三 15O Ⅲ 1 00 100 200 3O0 400 5OO 训 练 集 图 3 各模型对训练样本 的拟合结果 从 图 3 可 知 ，相 对 于 GA—RBFNN、PSO—RBFNN，BPSO— RBFNN的拟合效果 明显更优 ，拟合值与实际 的网络流量之 问的 误差更小 ，这主要 由于 BPSO算 法在历 次迭 代过 程 中追 踪全 局 络流量时 间序列变成多维时间序列 。首先采用互信法对延迟时 最优 的同时追踪全局最差粒子 的反 向粒子 ，使收敛速度加快 ，跳 间 ( )进行求解 ，结果 如 图 2(a)所示 。从 图 2可 知 ，当 =6 时 ，互 信息函数达到第一极小 值 ，所 以网络流量时间序列的最优 r=6。 网 络 流 量 时 间 序 列 在 不 同 嵌 入 维 数 下 的 关联 维 数 ，如 图 2(b)所示。从 图 2(b)可知 ，随着嵌 入维数 的增加 ，关联维 数不 断增加 ，当嵌 入维数 m =4时 ，关联维数达 到饱和状 态 ，说 明 网 络流量时间序列重构相空 间的最佳嵌入维数为 m =4。从图 2可 氍 匿 知 ，采用最 优的 ：6，m ：4对 网络流量时间 序歹lj进行相空 间重 如 。 构 ，得到 RBF神经 网络 的学 习和测试样本 。 出局部最优能力增强 ，可以找 到更 优 的 RBFNN参 数 ，建 立 的网 络流量预测模 型可拟合 网络流量 的时变性 、混沌性变化特点 ，拟 合精度得 以提高 。 (2)网络 流 量预 测 结 果 对 比 模 型性 能好 坏 主 要通 过 其预 测 能力 进 行衡 量 ，采 用 GA— RBFNN、PSO—RBFNN和 BPSO—RBFNN 对 测 试 样 本 进 行 预 测 ，预 测 结 果 如 图 4所 示 。 E 0．8 × O．6 { 5 10 15 T (a)计算延迟时间(r) nql (b)计 算嵌 入维 (卅) 图 2 计算 延迟 时 间 (r)和嵌 入 维 (m) 2．5 结 果与 分析 (1)网 络 流 量 拟 合 结 果 对 比 图 4 各 模 型 对 测 试样 本 的 预测 结 果 从 图 4可知 ，相对 于对比模 型 ，BPSO—RBFNN降低 了网络流 量实验值 与预测值 问的误差 ，较对 比模型预测结果要小 ，对 比结 果表 明，采用 BPSO算法优化 RBFNN，克 服 了局 部极小 的束缚 ， 能够有效地进行全局寻优 ，提高了网络流量预测精度 ，预测结 果 更 加 令 人 满 意 。 (3)综合 性 能 评 价 计算 3种 网络流量模 型对训 练样本 、测试样 本拟合 和 预测 的 RMSE、MPAE 值 ，结 果 见 表 1所 示 。 从 表 1可 知 ，BPSO— RBFNN 的 各 项 标 准 均 要 优 于 GA—RBFNN、PSO—RBFNN，这 说 明 BPSO．RBFNN构 建 网 络 流 量 预 测 模 型 克 服 了 GA、PSO 优 化 RBFNN参数时存 在的缺陷 ，进一步提高 了网络 流量 预测精度 。 表 1 几 种 预 测 模 型 的 综 合 性 能 对 比 将训练样本输入 到 RBF神经 网络进行 训练 ，然后分别采 用 BPSO算法 、遗传算法 、PSO算 法进行参 数优 化 ，最后采用相应 的 参数建立 BPSO—RBFNN、GA-RBFNN、PSO—RBFNN的网络流量预 测模型 ，并对训 练样 本 的输 出值 进行 拟 合 ，得 到 的结果 如 图 3 3 结 语 所 示 。 针 对 网络 流 量 预 测 的 RBFNN参 数 优 化 问 题 ，采 用 BPSO优 

第 9期 王雪松 等 ：基 于 BPSO．RBF神 经 网络 的 网络流 量预 测 105 化 RBFNN参 数 ，建立 了一种 BPSO—RBFNN的 网络流量 预测模 良恶性分类有更便捷 、准确率更高 的分类效果 。 型 ，并通过仿真实验验证有效性 ，预测结果可 以为 网络管理提供 有价值的参考意见。 3 结 语 参 考 文 献 本文 的贡献是针对孤立性肺结节难 于定性 问题 提出了一 种 魏先 民．网络流量预测 的组合 方法研究 [J]．计 算机应 用与软 件 ， 新颖 的基 于 PSO—SVM 的肺结节分类模 型 ，其基本思想是建立 在 2012，29(9)：139—142． [2] Ames T，Rego C，Glover F．Muhistart tabu search and diversification strategies for the quadratic assignment problem[J]．IEEE Transactions on Systems，Man，and Cybernetics：Part A Systems and Humans，2009， 39(11)：579—596． [3] 高波 ，张钦宇 ，梁永生 ，等．基 于 EMD及 ARMA的 自相似 网络流量 预测 [J]．通 信学报 ，2011，32(4)：47—56． [4] Este A ，Gringoli F，Salgarelli L．Support vector machines for TCP traffic 使用肺结 节 PET／CT影像 特征分 级量 化作 为数据 源 ，利用粒 子 群算 法对 支持 向量 机进 行参数搜 索进 而选择最合 适 的参 数 ，最 终得到分类精 度更 高 的支 持 向量 机分类模 型 。医生在 阅片 时 ， 受个人经验 与知识 的影 响 ，不能有效 利用结 节的所有 影像学 特 征 ，仅注重有 限的几个特征 ，影响了诊 断的准确率。而优 化后 的 支持向量 机(PSO—SVM)可 比较一致地综合 CT和 PET所有 信息 进行归纳 ，综合鉴别能力优于一般的分类模型 ，也 可给阅片医师 classification[J]．Computer Networks，2009，53(14)：2476～2490． 尤其 是经 验不 足的年轻 医师提供 理论参 考。 [5] 熊南 ，刘百芬．基于 自适应 粒子群优化 LSSVM 的网络流量在 线预 测 [J]．计算机应用与软件 ，2013，30(9)：21—24，127． 参 考 文 献 [6] Callado A，Keu R J，Sadok D，et a1．Better network traffic identification 美 国 癌 症 学 会 官 网 ．http：／／www．cancer．org／Cancer／news／News／ through the independent combination of techniques[J]．Journal of Net— annualreport—u．s-cancer·death—rates—decline—but—disparities remain． work and Computer Applications，2010，33(4)：433—446． [2] Soubani AO．The evaluation and management of the solitary pulmonary [7] Silva C G．Time series forecasting with a nonlinear model and the scat- nodule[J]．Postgrad Med J，2008，84(995)：459—466． ter search mcta．heuristic[J]．Information Sciences，2008，178(16)： [3] Rens M T，Riviere A B，Eibets H R，et a1．Prognostic assessment of 3288—3299． 2，361 patients who underwent pulmonary resection for non—small cell [8] Wang W S。Jin J J．“ Y Q．Prediction of inflow at three gorges dam in lung cancer，stage I，Ⅱ，ⅢA[J]．Chest，2000，l17(2)：374—379． Yangtze River with wavelet network model[J]．Water Resources Man- [4] Varoli F，Vergani C，Caminiti R，et a1．Management of solitary pulmo agement，2009，23(13)：2791—2803． nary nodule[J]．Eur J Cardiothorac Surg，2008，33(3)：461—465． [9] 赵振江 ．基于 PSO—BP神经 网络 的网络流量预测 与研究 [J]．计算 [5] Lonsdale，Markus Nowak． Dual-modality PET／CT instrumentation—To— 机应 用 与软 件 ，2009，26(1)：218—211． day andtomorrow[J]．European Journal ofRadiology，2010，73(3)： [1O] 陈政 ，杨天奇．基于 RBF神经网络 的股 票市场预测 [J]．计算 机应 452—460． 用与软件 ，2010，27(6)：108一ll0． [6] Yu Huan，Caldwell Curtis，Mah Katherine，et a1．Automated Radiation 赵清艳 ，熊茂华．混沌粒子群优化神经网络在铁路 客运量预测 中的 Targeting in Head-·and··Neck Cancer Using Region·Based Texture Anal-· 应用 [J]．计算机应用 与软件 ，2013，30(6)：225—227，242． ysis of PET and CT Images[J]．International Journal of Radiation On- (上 接 第 52页 ) cology Biology Physics 2009，75(10)：618—625． [7] Tom，Mitchel1． Learning to decode cognitive states from brain Images 表 3 未 优 化 的 支持 向 量机 分 类 结 果 [J]．Machine learning，2004，145—175． ＼ ＼ 样本总数 正确个数 错误个数 分类准确率／％ 恶 性 结 节 25 20 良性 结 节 19 全 部 结 节 44 15 35 5 4 9 80 78．9 79．5 经 过 1．4节所述 步 骤进 行参 数优 化 得 出的最 优参 数 C= 7．0032，o-=0．6102，由此得到的孤 立性肺结 节 良恶性分类 结果 ， 如 表 4所 示 。 [8] M Arran，Jaffar Ayyaz，Hussain Fauzia． GA—SVM Based Lungs Nodule Detection and Classification『J]．Communications in Computer and In． formation Science，2009，V61：133— 144． [9] Kennedy J，Eberhart R C，Shi Y．Swarm intelligence[M]．San Fran- cisco：Morgan Kaufm Publishers，2001． [10] Dautenhahn K．Book review：Swarm intelligence[J]．Genetic Program— ming and Evolvable Machines，2002，3(1)：93—97． 张 晓南 ，刘安心 ，刘斌 ，等．基 于优化 PSO—SVM模 型的软件可靠 性 预测[J]．计算机应用 ，2011，31(7)：1762—1764． [12] Vapnik V N．The nature of statistical learning theory[M]．New York： Springer—Verlag，2000． 表 4 优 化 后 的 支 持 向 量 机 分 类结 果 [13] Kennedy J，Eberhart R．Particle Swarm Optimization[C]／／IEEE In— ＼ ＼ 样本总数 正确个数 错误个数 分类准确率／％ tern ational Conference on Neural Networks Proceedings，Perth，W A ： 恶 性 结 节 25 良性 结 节 l9 22 18 全 部 结 节 44 40 3 1 4 88 94．7 90．9 IEEE，1995：1942—1948． [14] 胡旺，李 志蜀 ．一种更简化而高效的粒子群优化算法 [J]．软件 学 报 ，2007，18(4)：860—868． [15] 王琼芳．B超 图像 的乳腺肿瘤计算 机辅助诊断 系统研究 [D]．四 川师范大学 ，2009． [16] Ahmadian A ，Mostafa A ，Abolhassani M D，et a1．A method for rex— 对 比以上数据 可知 ，尽管使用了数量不大的样本集合 ，但 由 ture classification of ultrasonic liver images based on Gabor W avelet 于粒子群算 法对 支持 向量 机参数 的优化是 连续 的，所 以最后能 [c]／／2004 7th International Conference on Signal Processing，2004， 得到使 分类精度更好 的优化参数 ，所 得模型对 孤立性肺 结节 的 2 1971—974．