论文研究-混合电能交易市场中考虑电网负载均衡的最优化电能调度研究 .pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.91M 资料格式：pdf 举报版权申诉

weixin_39841848-11579170-4744302543405925356.pdf-第1页.png

第1页 / 共13页

weixin_39841848-11579170-4744302543405925356.pdf-第2页.png

第2页 / 共13页

weixin_39841848-11579170-4744302543405925356.pdf-第3页.png

第3页 / 共13页

weixin_39841848-11579170-4744302543405925356.pdf-第4页.png

第4页 / 共13页

weixin_39841848-11579170-4744302543405925356.pdf-第5页.png

第5页 / 共13页

weixin_39841848-11579170-4744302543405925356.pdf-第6页.png

第6页 / 共13页

weixin_39841848-11579170-4744302543405925356.pdf-第7页.png

第7页 / 共13页

weixin_39841848-11579170-4744302543405925356.pdf-第8页.png

第8页 / 共13页

文本预览

中国科技论文在线 http://www.paper.edu.cn 混合电能交易市场中考虑电网负载均衡的最优化电能调度研究# 陈佳超，吴远，郭款阳，严雨桐，彭宏** （浙江工业大学信息工程学院，杭州 310023）摘要：智能电网被认为是一种先进的电网系统，其中的电能消耗者与分布式电能供给者不仅能够连接外部电网公司进行电能交易，同时还能够连接以微电网等为代表的局部交易中心进行局部电能交易，从而以更加“多元”灵活的方式获取或者供给宝贵电能。本文考虑一个由外部电力公司和多个局部交易中心所组成的混合电能交易市场。本文的目标是研究如何在保证电网负载均衡条件下通过控制电能供给者和消耗者的电能调度以及局部交易中心的定价从而充分为电能供给者和消耗者服务、最大化他们的整体收益。为了实现这一目标，本文建立了一个最优化交易问题模型并且提出了一种能够得到局部交易中心最优定价方案以及每个电能供给者和消费者最优能耗调度的有效算法。数值仿真结果表明了所提出算法的性能以及混合电能交易市场机制的优势。关键词：计算机科学技术其他学科；智能电网；电力混合市场；电能调度；电网负载均衡中图分类号：TP399 Optimal Energy Scheduling of Hybrid Energy Trading Market with Considering Balance of Network CHEN Jiachao, WU Yuan, GUO Kuanyang, YAN Yutong, PENG Hong (College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023) Abstract: Smart Grid has been considered as an advanced power system, where distributed energy sellers and energy consumers are connected not only to the external utility company, but also to the local trading centers in micro-grid for energy trading. Therefore, energy sellers and energy consumers can perform the energy trading in a flexible manner. This paper investigates a hybrid energy trading market which is composed of an external utility company and some local trading centers. This paper aims to maximize the total benefit of all energy sellers and energy consumers while taking into account the trading-balance among different local trading centers. For this purpose, a joint optimization of the sellers' and consumers' energy scheduling and the pricing of the local trading centers is formulated, and an efficient algorithm is proposed to find the optimal solution. Numerical results are provided to validate the performance of the proposed algorithm and the advantage of the proposed hybrid energy trading market. Key words: computer science and technology; smart grid; hybrid energy trading market; energy scheduling; balance of power network 5 10 15 20 25 30 35 0 引言智能电网被认为是一种具有可靠性、稳定和经济等特点的先进电网，它将信息与能源技术结合，利用信息技术实现能源的高效调度[1]。智能电网的核心是建立在双向通信上的高效 40 需求响应机制，电能供给者和电能消费者能够灵活地调度它们的电能供应和电能消耗。对比于传统电网，智能电网能够在降低电网负载，节约能源，提高经济效益，保护环境等方面具有十分重要的作用[2]。现有的关于电能交易和需求响应机制的研究可以被归纳为两类。第一类主要研究在零售基金项目：高等学校博士学科点专项科研基金（新教师基金）（项目编号 20133317120002）作者简介：陈佳超(1990-)，男，硕士研究生，主要研究方向：无线网络数据分流、智能电网通信联系人：吴远，副教授，主要研究方向：通信与网络、智能电网. E-mail: iewuy@zjut.edu.cn - 1 -

中国科技论文在线 http://www.paper.edu.cn 市场中电能消费者的最优能耗调度，例如：在文献[3]中，作者研究住宅能耗调度机制，在最 45 小化电能代价和家用电器能耗之间进行权衡；在文献[4]中，作者提出优化终端用户的能耗调度，在最小化终端用户电能购置代价的同时保证电器的使用要求；在文献[5][6]中，作者研究大量电能消费者条件下如何利用非合作博弈以最小化电能消费者各自的电费。第二类主要研究电能供给者的定价策略，例如：在文献[7]中，作者研究提出考虑多个电能供给者和电能消 50 费者的斯坦伯格博弈方法，从而优化每个电能供给者的收益和每个电能消费者的电费；在文献[8]中，作者研究考虑在具有大量电动车背景下的“车-电网”市场中提出一种频率控制，并通过智能定价策略来激励电动车参与到这个控制机制中来；在文献[9]中，作者利用拍卖理论优化电动车和电网之间的电能交换。上述两类研究主要考虑的是电能消费者和外部零售市场之间的电能交易。事实上，未来的智能电网应该是一种混合系统，这个混合包括两层意思：1）不仅存在以电力公司为代表 55 的外部电能交易市场；同时存在以分布式电能供给、微电网为代表的局部电能交易中心；2）每个电能消费者（或供给者）不仅可以与外部市场进行电能交易、同时也能与局部电能交易中心进行电能交易[10][11]。对这一混合市场机制研究目前仍然是一个开放的问题，特别是相较于传统的外部电网，电能消费者和分布式电能供给者如何通过混合市场中的局部电能交易获得更多利益，这是一个有待深入研究的问题。在之前工作[12]中，我们尝试考虑只有一个 60 局部交易中心的混合市场并分析用户如何从中获益问题。但是这一问题在存在多个局部交易中心的情况下将变得更为复杂，因为在实际情况下，我们需要考虑到电能交易过程中，电能流在多个不同局部交易中心之间的负载平衡问题。针对这一问题，我们在本文中考虑在电能供给者和消费者能够同时与一个外部电网公司以及多个局部交易中心进行交易的情况下，最大化包括电能供给者和消费者在内的系统收益并且兼顾电网负载均衡。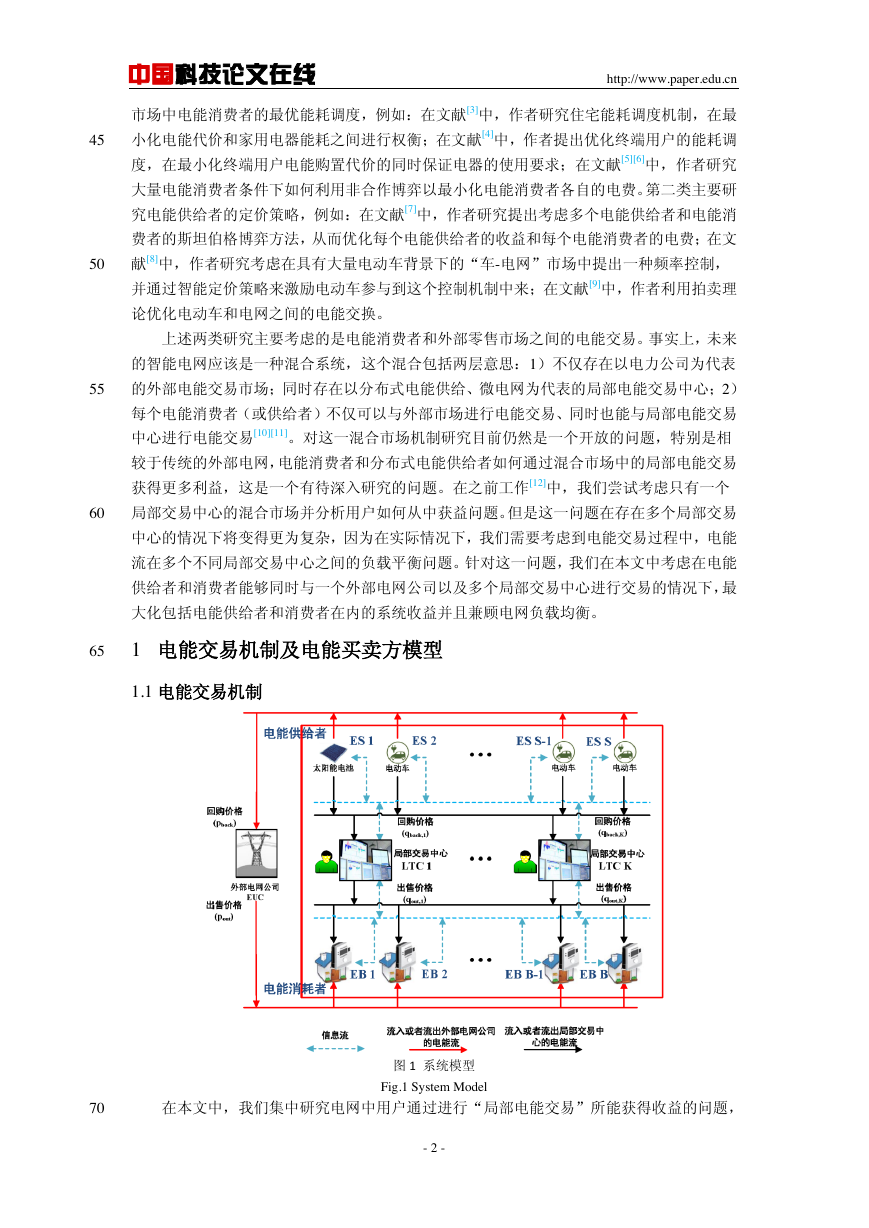 65 1 电能交易机制及电能买卖方模型 1.1 电能交易机制 70 在本文中，我们集中研究电网中用户通过进行“局部电能交易”所能获得收益的问题，图 1 系统模型 Fig.1 System Model - 2 -

中国科技论文在线 http://www.paper.edu.cn 为此我们考虑如图 1 所示的模型。在该模型中，存在两类用户，包括： i) 一组电能供给者（Energy Seller 简称为 ES）并用集合表示，每个 ES 都具有一定量的多余电能并期望进行出售而后获益； ii) 一组电能消费者或称购电者（Energy Buyer 简称 EB）并用集合表示， 75 每个 EB 具有一定量的电能需求期望通过购买获得。为实现电能交易，图 1 所示模型中具有两类交易控制单元，包括： i) 一个外部电网公司（External Utility Company 简称 EUC），EUC 向每个 ES 给出的电能回购单位价格用表示。EUC 向每个 EB 给出的电能出售单位价格用表示； ii) 一组局部交易中心（Local Trading Center 简称 LTC）并用集合表示。 80 每个 LTC 独立进行定价，即 LTC 向每个 ES 给出的电能回购单位价格用表示；LTC 向每个 EB 给出的电能出售单位价格用表示。后续问题建模过程中将用到的重要符号及变量已列举在表 1 中。表 1 符号及变量 Tab. 1 Symbols and Variables 符号含义 LTC 的集合 EB 的集合 ES 的集合 EB 从 LTC 购买的电能量 EB 的电能需求量 EB 从 EUC 购买的电能量 LTC 的电能出售单位价格 EUC 的电能出售单位价格 ES 卖给 LTC 的电能量 ES 的电能余量 ES 卖给 EUC 的电能量 LTC 的电能回购单位价格 EUC 的电能回购单位价格电网负载均衡上限当 EB 从 LTC 购买的电能时的电能传输损耗，当 ES 将的电能卖给 LTC 时的电能传输损耗，当 ES 将的电能卖给 EUC 时的电能传输损耗， 85 1.2 电能消费者模型如章节 1.1 所述，电能消费者 EB 具有一定的用电需求，需要通过选择向 EUC 和 LTCs 购买电能来满足需求。因此，我们定义每个 EB 的用电需求为，需要满足以下条件：， (1) 90 其中，表示 EB 从 EUC 购买的电能量，表示 EB 从 LTC 购买的电能量。函数表示当 EB 从 LTC 购买的电能时产生的电能传输损耗，本文用一个二次函 - 3 - {1,2,...,S}ssj{1,2,...,B}bbibackpoutpK{1,2,...,K}k,backkqk,outkqKbsikyikidiiExi,outkqkoutpjkyjjdjjExj,backkqkbackp()ikikfyikiky2()()ikikikikikikfyayby()jkjkfyjjkyk2()()jkjkjkjkjkjkfyayby()jEjEfxjjEx2()()jEjEjEjEjEjEfxaxbxbiidK(()),iEikikikibkxyfydiiExiikyik()ikikfyikiky

中国科技论文在线 http://www.paper.edu.cn 数来具体表示[13][14]，，根据此电能传输损耗的二次函数表达式可知，不同 EB 从不同 LTC 购电产生的电能传输损耗均不同。根据(1)式中 EB 的购电需求方案，进而我们可以表示出每个 EB 满足用电需求 95 所需要付出的总代价，如下所示：， (2) 其中，表示 EUC 的电能出售单位价格，表示 LTC 的电能出售单位价格。通过(1) 式和(2)式可以发现，对于每个 EB ，i) 当从 LTC 购电时，需要承担在传输过程中损耗的电能，即；ii) 当从 EUC 购电时，无须承担在传输过程中损耗的电能，因为 100 在现实生活中，用户的用电费用是直接根据每户的电表电量计算得到，不包括在线路上的电能传输损耗。接下来，我们考虑用户在“局部电能交易”机制下能够获得的净收益。因此，我们首先将不参与“局部电能交易”时的情况作为基准情况，即每个 EB 都不允许与任意 LTC 交易。在此基准情况下，EB 满足电能需求的代价可以表示为： 105 。 (3) 通过(2)式和(3)式的对比，我们可以得到在 EB 参与“局部电能交易”时可以获得的净收益，即：。(4) 此外，我们还规定，在“局部电能交易”中的每个 EB 净收益必须保证其非负，因此 110 有， 1.3 电能卖方模型。 (5) 根据章节 1.1 中所提到的，在“局部电能交易”中还有一类用户被称为电能供给者 ES ，能将一定量的多余电能选择向 EUC 和 LTCs 出售以达到获益目的。 115 同样地，我们定义 ES 的电能余量为，对于每个 ES 都需要满足以下条件：， (6) 其中，表示 ES 卖给 EUC 的电能量，表示 ES 卖给 LTC 的电能量。函数表示当 ES 将的电能卖给 LTC 时的电能传输损耗（中的下标用来区别 ES 与不同 LTC 间的电能传输损耗），表示当 ES 将的电能卖给 EUC 120 时的电能传输损耗。具体的，和可以分别表示为，。另外，我们也对在“局部电能交易”中的 ES 的收入进行数学表示，每个 ES 的收入可以表示为如下形式：， (7) 125 其中，表示 EUC 对从 ES 购电的电能回购单位价格，表示 LTC 对从 ES 购电的电能回购单位价格，下标体现了不同 LTC 对电能的回购单位价格也不同。此外由 - 4 - 2()()ikikikikikikfyaybyikbii,(,{}),iiEikkKiEoutikoutkbkKCxyxpyqioutp,outkqkikK()ikikfybikKi(,{0})iikKioutCddpbi,(,{})(,{0})(,{})(),iiEikkKiikKiiEikkKoutiiEikoutkbkKGxyCdCxypdxyqii(,{})0,iiEikkKbGxyisjsjjdj()(()),jEjEjEjkjkjkjskKxfxyfydjjExjjkyjk()jkjkfyjjkyk()jkjkfykj()jEjEfxjjEx()jkjkfy()jEjEfx2()()jkjkjkjkjkjkfyayby2()()jEjEjEjEjEjEfxaxbxsjj,(,{}),jjEjkkKbackjEbackkjkskKIxypxqyjbackpj,backkqkjk

中国科技论文在线 http://www.paper.edu.cn (6)式和(7)式可知，对于 ES 来说，i) 在卖给 EUC 电能时需要承担相应的电能传输损耗部分，即；ii) 在卖给 LTC 电能时需要承担相应的电能传输损耗部分，即。同时，为了量化参与“局部电能交易”中 ES 的收益，我们考虑将 ES 不与任 130 意 LTC 交易的情况作为基准情况。在此基准情况中，每个 ES 的收益可以表示为：根据(7)式和(8)式，我们可以得到当 ES 出售电能给 LTCs 时的净收益，即：。 (8) . (9) 135 同时，我们规定，ES 的净收益同样为非负，因此有，至此，根据章节 1.2 中的(1)式和章节 1.3 中的(6)式，电网中的总电能传输损耗可以表示。 (10) 为：， (11) 140 上式中，第一部分表示 ES 到 EUC 之间的电能传输损耗总和，第二部分表示 ES 到 LTC 之间的电能传输损耗总和，第三部分表示 LTC 到 EB 之间的电能传输损耗总和。 2 问题建模在本章节中，我们对章节 1 中提出的用户参与“局部电能交易”从而获益的问题进行建 145 模。我们规定 LTC 不从“局部电能交易中获益”，换句话说，每个 LTC 通过控制使得 EBs 和 ESs 尽可能多得获益。与此同时，LTC 各自控制的不会使其有经济损失，即需要满足以下条件：， (12) 其中，不等式左边部分表示 LTC 对所有 EBs 售电费用的总和，不等式右边表示 LTC 支 150 付给所有 ESs 购电费用的总和。在参与“局部电能交易”过程中，LTC 除了不会有经济损失，我们还规定 LTC 需要保持供需平衡，即对于每个 LTC 来说，还需要满足以下条件：。 (13) 另外，我们还考虑到当集合中的个别 LTC 相较于其他 LTC 出价过于优厚时，电网 155 中的大多数交易可能会集中到这些少数 LTC 上导致这部分 LTC 和相关电网负载过大。为了尽可能地避免这种情况的发生，均衡电网负载，我们定义电网负载均衡需要满足以下条件：， (14) 其中，表示电网当前负载均衡度，表示电网负载均衡上限，表示 LTC 的负载率均衡值，这里表示为。 - 5 - j()jEjEfxk()jkjkfysjjkKsj(,{0}),jjkKbackjsIdpdjsj,(,{})(,{})(,{0})(),jjEjkkKjjEjkkKjjkKbackjEjjkbackkskKGxyIxyIdpxdyqjsj(,{})0,jjEjkkKsGxyj()()()ssbjEjEjkjkikikjkKjkKifxfyfysjsjkkbikKkK,,(,)backkoutkqqk,,(,)backkoutkqq,,,bsoutkikbackkjkijqyqykKkkkKkk,bsikjkijyykKK2(),,jkkjsyyjkKK2()jkkjyyKy/Kjkkjyy

中国科技论文在线 http://www.paper.edu.cn 160 2.1 系统建模因此，基于章节 1.2 的 EB 模型和章节 1.3 的 ES 模型，以及公式(12)至(14)，我们建立考虑负载均衡条件下的局部电能交易优化模型（“MLTC”为“Multiple LTC”的简写），具体如下： 165 受约束于: ， (1) ， (5) ， (6) ， (10) ， (12) 170 ， (13) ， (14) ， (15) ， (16) 决策变量: 。 175 其中，表示负载均衡收益系数。函数表示 EB 在净收益下的效益。函数表示 ES 在净收益下的效益。问题(MLTC)表示所有 LTCs 协作地调整定价规则以最大化所有 EBs 和 ESs 通过局部电能交易获得的效益，具体的保证以下 2 点：i）每个 LTC 在局部交易过程中不会有经济损失（即(12)式）；ii）对于每个 LTC 来说，都各自保持供需平衡（即(13) 180 式）。约束条件(14)表示对电网中的负载控制在一定范围之内，尽可能地保证电网的稳定。约束条件(15)表示每个 LTC 的电能出售单位价格不能超过 EUC 的电能出售单位价格，这样每个 EB 才有兴趣与 LTC 交易。同样的，约束条件(16)表示每个 LTC 的电能回购单位价格不能低于 EUC 的电能回购单位价格，这样 ES 才有更大的兴趣与 LTC 交易。 185 特别地，为方便求解问题(MLTC)，我们提出以下重要特性。该重要特性的证明方法与我们之前的论文[12]中性质 2 的证明类似，这里不再赘述。请注意到，和论文[12]明显不同的是，在(MLTC)中，不同 LTC 可以有完全不同的价格选择。重要特性 1：当问题(MLTC)取到全局最优解时，对任意 LTC 必然有都成立。换言之，从全局系统最优的角度上看，所有 LTC 都将不会从协助电能消费者和电能 190 供给者之间的局部电能交易过程中获得任何经济收益，因为所有通过局部电能交易所获的收益都将被电能消费者和电能供给者分享，从而最大化系统效益。根据上述重要特性 1，问题(MLTC)中在约束条件(13)下，约束条件(12)能够始终被满足。问题(MLTC)的模型可以转变为下述问题（字母“E”表示等效），具体形式如下： - 6 - (MLTC):maximize((,{}))((,{}))bsiiiEikkKjjjEjkkKijUGxyUGxyK(()),iEikikikibkxyfydi(,{})0,iiEikkKbGxyi()(()),jEjEjEjkjkjkjskKxfxyfydj(,{})0,jjEjkkKsGxyj,,,bsoutkikbackkjkijqyqykK,bsikjkijyykK2(),,jkkjsyyjkKK,,outoutkpqkK,,backkbackqpkK,,K{,},{,},{,}bsbackkoutkkiEiijEjjqqxyxy()iUiK(,{})iiEikkGxy()jUjK(,{})jjEjkkGxy,,(,)backkoutkkKqqkkk,outkqoutpkk,backkqbackpkk,,backkoutkqq

中国科技论文在线 195 受约束于：(1)，(6)，(13)，(14)， http://www.paper.edu.cn ， (17) ， (18) ， (19) 决策变量: 。 200 其中，变量表示 LTC 的电能回购单位价格以及出售单位价格。问题(MLTC)中的约束条件(5)和(10)根据重要特性 1 转换为问题(MLTC-E)中的约束条件(17)和(18)，表示 EB 和 ES 的净收益都保证非负。问题 (MLTC)中的约束条件 (15)和 (16)转换为问题 (MLTC-E)中的约束条件(19)，表示 LTC 对电能的回购价格高于 EUC 的回购价格，以此吸引更多 ES 将电能卖给 LTC ，同时 LTC 对电能的出售价格低于 EUC 的出售价格， 205 以此吸引更多 EB 从 LTC 购电。但是，由于上述优化问题(MLTC-E)涉及到和多个决策变量的联合优化，直接求解整个问题非常复杂。为简化问题，研究将上述问题拆分为一个顶层问题和一个底层问题。其中，底层问题的目标是在给定 LTCs 的定价情况下，最大化考虑电网负载均衡在内的电能供给者和消费者的利益。顶层问题的目标是根据底层问题的结果，进 210 一步优化各个 LTC 的定价方案。 2.2 底层问题在给定 LTCs 定价的情况下，底层问题求解电能供给者和消费者的最优电能调度。因此，底层问题(MLTC-E-Bottom)建模如下： (MLTC-E-Bottom)： 215 受约束于：(1)，(6)，(13)，(14)，， (17) ， (18) 决策变量：。 220 底层问题(MLTC-E-Bottom)的求解将在章节 3.1 中进行介绍。 2.3 顶层问题得到底层问题(MLTC-E-Bottom)的结果，顶层问题(MLTC-E-Top)再进一步对 LTCs 的定价进行优化。顶层问题(MLTC-E-Top)建模如下： (MLTC-E-Top)： 225 受约束于：， (19) 决策变量：。顶层问题(MLTC-E-Top)的求解将在章节 3.2 中进行介绍。 - 7 - (MLTC):maximize((,{}))((,{}))bsiiiEikkKjjjEjkkKijEUGxyUGxy()0,outiiEikkbkKpdxyqi()0,backjEjjkkskKpxdyqj,outkbackpqpkKK{},{,},{,}bskkiEiijEjjqxyxykqkbisjkkkkK{},{,}bkkiEiiqxy{,}sjEjjxyK{}kkq({})maximize((,{}))((,{}))bskkKiiiEikkKjjjEjkkKijqUGxyUGxy()0,outiiEikkbkKpdxyqi()0,backjEjjkkskKpxdyqj{,},{,}bsiEiijEjjxyxyK{}kkqmaximize({})kkKq,outkbackpqpkKK{}kkq

中国科技论文在线 3 问题求解 http://www.paper.edu.cn 本章节分别对底层问题(MLTC-E-Bottom)和顶层问题(MLTC-E-Top)进行求解。 230 3.1 底层问题求解根据第 1 章和第 2 章的结果，我们可以知道，当给定 LTCs 的定价时，底层问题(MLTC-E-Bottom)具有如下特性：重要特性 2：当给定 LTCs 的定价时，底层问题(MLTC-E-Bottom) 关于决策变量是一个凸优化问题。 235 证明：在给定前提下，底层问题(MLTC-E-Bottom)的约束条件所构成的可行解区域为一个标准凸集合。因此根据文献[15]，当底层问题(MLTC-E-Bottom)的目标函数为凹并且约束条件所构成的可行解区域为凸集时，底层问题(MLTC-E-Bottom)是一个凸优化问题。基于上述重要特性 2，我们利用 MATLAB 中的 CVX[16]直接对底层问题(MLTC-E-Bottom) 进行求解。CVX 是一种基于 MATLAB 的能够有效求解凸优化问题的求解器。 240 3.2 顶层问题求解顶层问题(MLTC-E-Top)的目标是在得到底层问题(MLTC-E-Bottom)结果的基础上，进一步对 LTCs 的定价优化。对此，我们提出基于模拟退火的求解算法(A1)，具体流程如下：算法(A1)：求解顶层问题(MLTC-E-Top) 第一步：初始化起始温度，终止温度，降温系数，同一温度下最大迭代次数。第二步：随机生成一组 LTCs 的定价。第三步：利用 CVX，计算。更新当前 LTCs 定价，更新当前结果。第四步：若当前温度，执行第五步，否则执行第十三步。第五步：设置同一温度下当前迭代次数。第六步：若当前迭代次数，执行第七步，否则执行第十二步。第七步：随机生成一组 LTCs 的定价。第八步：利用 CVX，计算。设置。第九步：判断是否，若是，更新当前 LTCs 定价，更新当前结果，执行第十一步；若否，执行第十步。第十步：在区间[0,1]生成随机数，当时更新当前 LTCs 定价，更新当前结果第十一步：设置第十二步：设置并执行第十一步，否则直接执行第十一步。，并返回第六步。，并返回第四步。第十三步：输出：顶层问题的值，以及对应的 LTCs 定价。在算法(A1)中，主要包括两个循环，一个外循环和一个内循环，其中外循环从第四步到 245 第十二步，内循环从第六步到第十一步。算法(A1)在初始化（第一步）后，首先生成一组初 - 8 - K{}kkqK{}[,]kkbackoutqpp{,},{,}bsiEiijEjjxyxyK{}kkqK{}kkq1000.01stop0.9510NK{}[,]kkbackoutqpp({})kkKqK{}kkqS({})kkKOq>stop0nnN'K{}[,]kkbackoutqpp'({})kkKq'({})kkKOq'({})OkkKq'K{}kkqS'({})kkKOqe'K{}kkqS'({})kkKOq1nnOS

分享到：

赞收藏

资料库

论文研究-混合电能交易市场中考虑电网负载均衡的最优化电能调度研究 .pdf

相关推荐

开发技术

热门标签

最新资料