2 2 微电机 中图分类号 : TM36 + 1　　　　　　文献标志码 : A　　　　　　文章编号 : 1001 2008年第 41卷第 3期 6848 (2008) 03 0052 04 无刷直流电动机分数槽集中绕组 槽极数组合选择与应用 (连载之四 ) 谭建成 (广州电器科学研究院 , 广州 　510300) 摘 　要 : 在文献 [ 1 ]基础上 , 继续展开对分数槽集中绕组槽极数组合的讨论 , 分析影响槽极数组 合选择的若干制约因素 , 如奇数槽或偶数槽 、单层绕组或双层绕组 、绕组磁势谐波与转子涡流 损耗 、组合的最小公倍数和齿槽转矩 、绕组排列与径向不平衡磁拉力 、纹波转矩等 。结论可供 设计者参考 。 关键词 : 无刷直流电动机 ; 集中绕组 ; 槽极数组合 ; 转子涡流损耗 ; 径向不平衡磁拉力 ; 纹波 转矩 Selection of Slot/Pole Num ber Com b ina tion s for BLDCM w ith Concen tra ted W ind ings ( Guangzhou Electrical Apparatus Research Institute, Guangzhou 510300, China) TAN J ian cheng Abstract: This paper analysed selecting factor of slot/pole number combinations for BLDCM with concen trated windings, discussed harmonics in MMF, rotor eddy current loss, LCM and cogging torque, unbalanced and Key W ords: BLDCM; Concentrated w inding; Slot/pole number combination; Rotor eddy current loss; Unbalanced layer configurations of concentrated windings. pull; Torque ripp le torque ripp le, magnetic magnetic pull, single double 4　Z 为奇数的 Z / p组合与磁拉力 (UMP) 问题 　　观察表 2和表 5发现 , 与 Z 为偶数的 Z / p组合 相比 , Z 为奇数的 Z / p组合更有优势 : 有较多的选 择机会 , 有较高的绕组系数 , 有较大的 LCM , 即 齿槽转矩较小 。但是有文献指出 , Z 为奇数的 Z / p 组合不推荐使用 , 因为它们存在不平衡径向磁拉 力 (UMP)问题 。 表 7是 Z 为奇数的单元电机双层绕组排列表 。 的组合 , 它们是符合 Z0 = 2p0 ±1 的 组合 注意表中有 基本组合 。观察表 7绕组排列发现 , 这些有 的绕组排列有相同规律 : 沿着电机气隙圆周 360° 分为三个区 , 每相线圈集中到约 120°的一个区内 。 这样 , 对每一相绕组来说 , 在气隙圆周上的分布 是偏向一边的 , 不平衡的 。 在径向磁场电动机气隙中 , 电磁效应产生的 切向力 、径向力和磁致伸缩力都会引起电磁噪音 。 切向力产生定子和转子之间的有用电磁转矩 , 而 径向力是在定子和转子之间的吸引力 , 磁致伸缩 力在磁场的方向对铁心的拉伸力 。径向力是径向 磁场 PM 电动机电磁噪音的主要来源 。在电机运转 时 , 偏置的相绕组产生偏置的定子电枢反应磁场 , 它和在气隙中永磁转子产生的磁场合成为不平衡 的合成磁场 , 产生不平衡的径向磁应力 , 称为不 平衡径向磁拉力 (UMP) 。随着电机的换相 , 这种 不平衡径向磁拉力是旋转的 , 每经过一个电气换 相周期 (6个状态 ) , 不平衡径向磁拉力旋转一周 , 其频率为电动机转子旋转频率的 p倍 , 引起电机高 频振动和噪音 , 如果转子在机械上还存在偏心 , 振动和噪音将加剧 。 举例来说 , 文献 [ 2 ]针对一台 Z /2p = 15 /14电 机用有限元法得到电机通电时的径向磁拉力分布 图 (图 6) , 显示出明显的不平衡的径向磁拉力 , 会 引起定子 (和转子 ) 的单向偏移 。所以该文认为 : 不宜选取那些槽数和极数接近而槽数是奇数的组 合 , 如 Z /2p = 9 /8、15 /14、21 /22等 。 　　收稿日期 : 2007 ·25· 01 19 

3 无刷直流电动机分数槽集中绕组槽极数组合选择与应用 　谭建成 图 6　Z /2p = 15 /14的径向磁拉力分布 为了解决这个问题 , 可考虑采取如下措施 : 1)优化电机设计参数 , 降低 UMP和它的影响 例如 , 为设计高性能硬盘 , 解决原先采用的 9 /8组合的硬盘主轴电动机不平衡磁拉力引起振动 和径向跳动已经变得十分迫切 。文献 [ 5 ]提出降低 UMP引起振动的坚固设计方法 。通过优化电机设 计参数 , 使 UMP影响减到最少 , 并注意提高制造 质量 , 降低如槽口制造偏差 , 和减少由于磁钢磁 化工装和磁化过程引起转子磁密分布的变化 。 日本东方马达株式会社在开发小型无刷电机 时 , 对比了几种 9槽电机方案 , 指出 Z /2p = 9 /8和 9 /10方案在绕组系数和齿槽转矩方面有较高性能 , 但是它们会产生径向不平衡电磁力 , 可能产生严 重的振动和噪声 。采用有限元法分析结果 , 运行 时径向不平衡电磁力变化频率是转子旋转频率的 p 倍 , 发现在相同电磁转矩条件下 9 /8电机产生的径 向不平衡电磁力比 9 /10电机产生的径向不平衡电 磁力大许多 , 约 4 倍 。该公司在 42 mm 机座号小 型无刷电机新产品中改用了 9 /10 槽极配合方案 , 并且在驱动器采用了正弦波驱动方式 , 进一步降 低电机的振动和噪声 [ 6 ] 。 2) 改用 Z 为偶数的槽极组合 著名硬盘制造商昆腾公司早在 1997年就发现 , 过去它们的硬盘无刷电动机采用的 9 /8组合存在不 平衡径向磁拉力 (UMP)问题 , 影响硬盘机性能的 提高 。昆腾公司将他们的硬盘无刷电动机方案改 换为 12 /10组合 , 以提高硬盘机工作的平稳性 , 并 申请了美国专利 [ 7 ] 。 应当指出 , 上述关于 Z 为奇数的 Z / p组合存 在不平衡径向磁拉力 (UMP)问题 , 只是对于单元 电机数 t = 1的组合 (即表 7中带 的组合 )才存在 。 这些组合表示在表 2和表 5中是带有阴影的组合 。 所以 , 可采取下面两个途径回避不平衡径向磁拉 力问题 。 1) 选择多个单元电机组合 对于表 7中带 的 Z0 为奇数的单元电机 , 如 果取单元电机数 t≧ 2, 对应的 Z / p组合并不存在 1 1 不平衡径向磁拉力 (UMP)问题 , 例如 Z / p = 18 /10 组合 。它由两个 9 /5组合单元电机组成 , 即 t = 2, 参见表 9, 绕组分布没有不平衡问题 。这样 , 可参 见文献 [ 1 ]的表 3, 选择 Z ≧ 18的那些组合 , 它们 的 单 元 电 机 是 9 /4、 9 /5、 15 /7、 15 /8、 21 /10、 21 /11, …, 的组合 。这些组合由于其单元电机的 Z0 为奇数 , 具有较高绕组系数 、较大 LCM , 较小 齿槽转矩的优点 。表 6给出了这样的例子 。第 1和 第 2行有相同槽数 , 极数也相近 , 9 /4的单元电机 是 Z0 为奇数的组合 , 则有较小的齿槽转矩 。绕组 系数方面 , Z0 / p0 = 12 /5 的 Kw = 0 933, 而 9 /4 的 Kw = 0 945, 稍大 。 2) 选择非基本组合的其他组合 带 的组合是 Z 为奇数的 Z / p组合中的基本 组合 , 即符合 Z0 = 2p0 ±1的组合 , 如文献 [ 1 ]的表 3所示 。对于 Z ≧ 21、槽数 Z 为奇数的每个 Z列 中 , 除了两个基本组合外 , 还有其他的 Z / p组合 可以选择 , 参见表 2。虽然它们的绕组系数不如基 本组合高 , 但绕组分布已不存在不平衡径向磁拉 力问题 。参见表 7, 如 21 /8、 21 /13、 27 /10、 27 / 11、 27 /16、 27 /17、 33 /13、 33 /14、 33 /19、 33 / 20, …, 可选取使用 。 5　负载下的波纹转矩 降低永磁电机转矩波动在精确的转速和位置 控制系统是一个十分关注的问题 。 如果永磁电机的绕组反电势和电流波形都是 正弦的 , 将获得平滑的转矩 , 没有转矩波动 。理 想情况是电机的空载气隙磁密是正弦分布 , 定子 绕组沿气隙也是正弦分布的 。分数槽集中绕组虽 然绕组感生的电势有可能接近正弦波 , 但由于其 极数和槽数很接近 , 绕组分布远不是正弦的 , 定 子磁势包含丰富的谐波 , 从而产生齿槽转矩和动 态转矩波动 。齿槽转矩是由于气隙磁导变化产生 , 而负载时 , 定子磁势谐波与转子磁场谐波相互作 用产生波纹转矩 , 它汇同齿槽转矩产生电机的转 矩波动 。此外 , 如果存在磁路磁阻不均衡 , 也可 能产生磁阻转矩 , 增加电机的转矩波动 。 一般而论 , 降低电机转矩波动从改进电机设 计和改变驱动器电流波形两个方面着手解决 。 学者 P. Salm inen研究了几种齿槽组合下集中 绕组电机的波纹转矩 , 指出合适的磁极宽和槽口 宽可以明显降低电机的波纹转矩 [ 8 ] 。其研究对象 是一个低速 400 r/m in目标样机 , 分别采用槽数为 36、24、18、12、 q = 0 25 几 种 不 同 组 合 , ·35· 5 ～0 

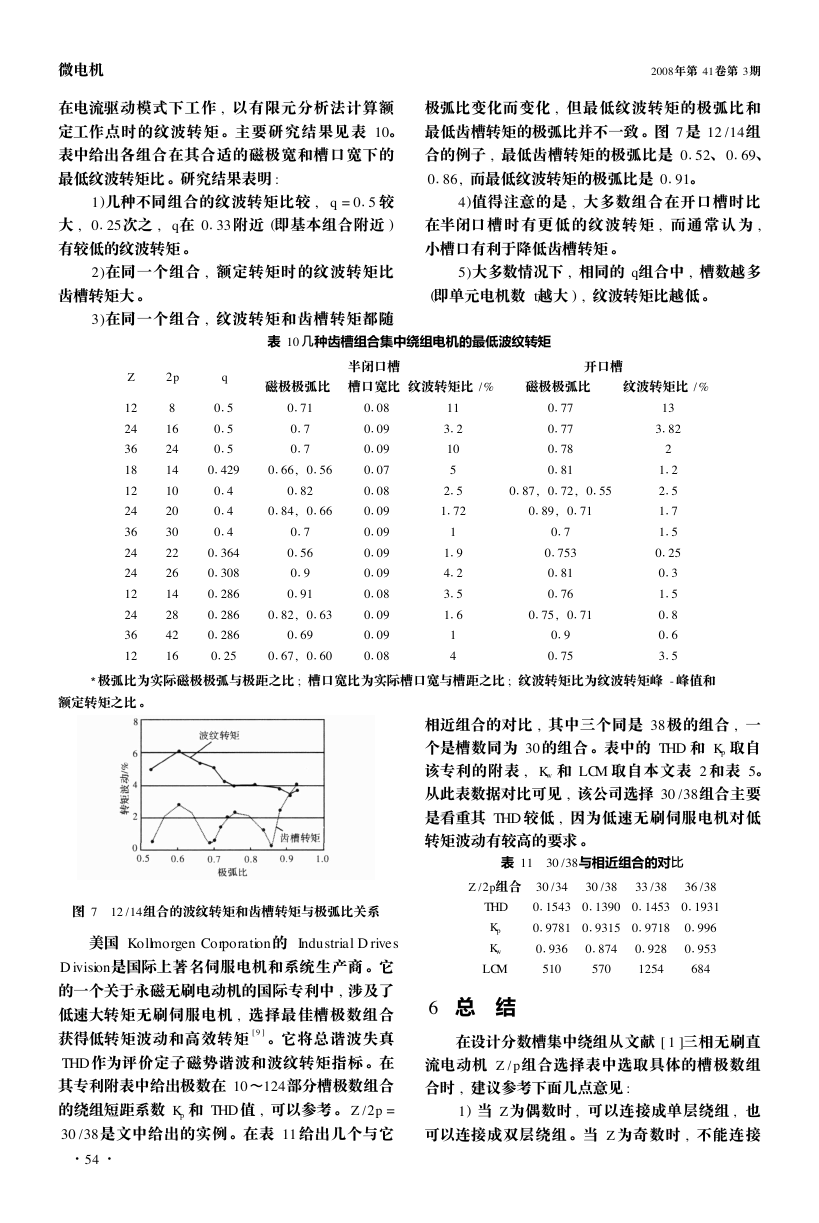
1 1 1 1 1 1 1 1 1 1 1 1 2008年第 41卷第 3期 极弧比变化而变化 , 但最低纹波转矩的极弧比和 最低齿槽转矩的极弧比并不一致 。图 7 是 12 /14组 合的例子 , 最低齿槽转矩的极弧比是 0 0 86, 而最低纹波转矩的极弧比是 0 52、0 91。 69、 微电机 在电流驱动模式下工作 , 以有限元分析法计算额 定工作点时的纹波转矩 。主要研究结果见表 10。 表中给出各组合在其合适的磁极宽和槽口宽下的 最低纹波转矩比 。研究结果表明 : 1)几种不同组合的纹波转矩比较 , q = 0 5 较 33附近 (即基本组合附近 ) 25次之 , q在 0 大 , 0 有较低的纹波转矩 。 4)值得注意的是 , 大多数组合在开口槽时比 在半闭口槽时有更低的纹波转矩 , 而通常认为 , 小槽口有利于降低齿槽转矩 。 2)在同一个组合 , 额定转矩时的纹波转矩比 5)大多数情况下 , 相同的 q组合中 , 槽数越多 齿槽转矩大 。 (即单元电机数 t越大 ) , 纹波转矩比越低 。 3)在同一个组合 , 纹波转矩和齿槽转矩都随 Z 12 24 36 18 12 24 36 24 24 12 24 36 12 2p 8 16 24 14 10 20 30 22 26 14 28 42 16 q 5 5 5 429 4 4 4 364 308 286 286 286 25 0 0 0 0 0 0 0 0 0 0 0 0 0 表 10 几种齿槽组合集中绕组电机的最低波纹转矩 半闭口槽 开口槽 磁极极弧比 槽口宽比 纹波转矩比 / % 磁极极弧比 纹波转矩比 / % 0 0 0 71 7 7 66, 0 0 82 84, 0 7 0 56 0 9 0 0 91 82, 0 0 69 67, 0 0 0 0 0 56 66 63 60 0 0 0 0 0 0 0 0 0 0 0 0 0 08 09 09 07 08 09 09 09 09 08 09 09 08 0 11 3 2 10 5 2 1 5 72 1 1 4 3 1 9 2 5 6 1 4 0 0 0 0 87, 0 0 77 77 78 81 72, 0 71 89, 0 0 7 753 0 81 0 0 76 75, 0 9 75 0 0 0 71 55 13 82 3 2 1 2 1 1 0 0 1 0 0 3 2 5 7 5 25 3 5 8 6 5 极弧比为实际磁极极弧与极距之比 ; 槽口宽比为实际槽口宽与槽距之比 ; 纹波转矩比为纹波转矩峰 - 峰值和 　　 额定转矩之比 。 相近组合的对比 , 其中三个同是 38极的组合 , 一 个是槽数同为 30的组合 。表中的 THD 和 Kp 取自 该专利的附表 , Kw 和 LCM 取自本文表 2 和表 5。 从此表数据对比可见 , 该公司选择 30 /38组合主要 是看重其 THD 较低 , 因为低速无刷伺服电机对低 转矩波动有较高的要求 。 图 7　12 /14组合的波纹转矩和齿槽转矩与极弧比关系 美国 Kollmorgen Corporation的 Industrial D rives D ivision是国际上著名伺服电机和系统生产商 。它 的一个关于永磁无刷电动机的国际专利中 , 涉及了 低速大转矩无刷伺服电机 , 选择最佳槽极数组合 获得低转矩波动和高效转矩 [ 9 ] 。它将总谐波失真 THD作为评价定子磁势谐波和波纹转矩指标 。在 其专利附表中给出极数在 10～124部分槽极数组合 的绕组短距系数 Kp 和 THD值 , 可以参考 。 Z /2p = 30 /38是文中给出的实例 。在表 11 给出几个与它 ·45· 表 11　30 /38与相近组合的对比 Z /2p组合 30 /34 30 /38 33 /38 1453 0 1390 0 0 9718 9315 0 0 874 928 0 1254 570 36 /38 1931 996 953 684 THD Kp Kw LCM 0 0 0 1543 0 9781 0 936 0 510 6　总 　结 在设计分数槽集中绕组从文献 [ 1 ]三相无刷直 流电动机 Z / p组合选择表中选取具体的槽极数组 合时 , 建议参考下面几点意见 : 1) 当 Z 为偶数时 , 可以连接成单层绕组 , 也 可以连接成双层绕组 。当 Z 为奇数时 , 不能连接 

无刷直流电动机分数槽集中绕组槽极数组合选择与应用 　谭建成 成单层绕组 , 只能连接成双层绕组 。和双层集中绕 组相比 , 单层集中绕组通常有较多的磁势 (MMF) 谐波 , 易产生较大的振动和噪声 , 而且电阻和电 感稍大 , 绕组端部较长 。一般推荐采用双层绕组 。 2) 不推荐选用单元电机数 t = 1且 Z 为奇数的 基本组合 (表 2 和表 5 有阴影的组合 ) , 它们存在 不平衡径向磁拉力 (UMP)问题 , 但其余 Z 为奇数 的组合可以选用 。 3) 利用表 2查询三相分数槽集中绕组 Z / P组 合的双层绕组绕组系数 。表中每个 Z 列 , 最上面 的组合是 q = 1 /2, 最下面的组合是 q = 1 /4, 它们 的绕组系数最低为 0 866; 中间位置是基本组合 , q在 1 /3附近 , 有最高绕组系数 。一般 , 从中间向 两边变化 , 绕组系数呈现逐渐降低的变化 。 4) 如果特别关注电机的齿槽转矩 , 宜选择定 子槽数 Z 和极对数 2p的最小公倍数 (LCM )较大的 组合 。利用表 5对拟选择的槽极数组合的齿槽转矩 强弱作初步评估 。一般 , 表中每个 Z 列 , 从中间 向下 , 即 q从 1 /3 附近向 1 /2 变化 , LCM 逐渐增 加 。选取表中黑体字对应的是单元电机组合将有 较大的 LCM , 和同一个 Z 列的组合相比较 , 它们 会有更低的齿槽转矩 。 5) 负载下纹波转矩比较 , q = 1 /2 较大 , 1 /4 次之 , q在 1 /3附近 (即基本组合附近 )有较低的纹 波转矩 。相同 q的组合中 , 大多数情况下 , 槽数越 多 (即单元电机数 t越大 ) , 纹波转矩比越低 。 6) 和整数槽绕组电机相比 , 分数槽绕组电机 通电绕组产生更多空间谐波和时间谐波的磁势 , 是负载时产生转矩波动原因 , 而且谐波磁势作用 下将会在转子产生涡流并造成损耗 , 最好能够对 拟选用的槽极数组合进行磁势谐波分析 , 选择总 谐波失真 THD较低的组合 。 参考文献 [ 1 ] 　谭建成. 三相无刷直流电动机分数槽集中绕组槽极数组合规 律的研究 [ J ]. 微电机 , 2008, 41 (1) : 52 55. [ 2 ] 　Freddy Magnussen, Dm itry Svechkarenko, Peter Thelin, Analy sis of a PM Machine with Concentrated Fractional Pitch W indings [ J ]. Proceedings of the Nordic Workshop on Power and Industrial Electronics (NORp ie) , June 2004. [ 3 ] 　D. Ishak, Z. Q. Zhu, D. Howe. Eddy Current Loss in the Rotor Magnets of Permanent - Magnet B rushlessMachines Having a Fractional Number of Slots Per Pole[ J ]. IEEE Transactions on Magnetics, 2005, 41 (9). [ 4 ] 　H. Polinder. Eddy Current Losses in the Solid Back iron of PM Machines for D ifferent Concentrated Fractional Pitch W indings, pol2007, IEEE: 652 657. [ 5 ] 　Xianke Gao. Robust Design for Unbalanced magnetic pull Op tim i zation of H igh Performance BLDC Sp indle Motors U sing Taguchi Method [ J ]. IE ICE TRANSACTIONS on Electronics, 2005, E84 C (9) : 1182 1188. [ 6 ] 　高宏伟. 无刷直流电动机的径向不平衡电磁力对振动噪声的 影响及其削弱方法 [ J ]. 微特电机 , 2007, (4). (未完待续 ) ·55·