小波变换轮廓术中用小波脊系数幅值引导相位展开的研究.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：3.64M 资料格式：pdf 举报版权申诉

weixin_38740144-15209420-4744300845399269797.pdf-第1页.png

第1页 / 共7页

weixin_38740144-15209420-4744300845399269797.pdf-第2页.png

第2页 / 共7页

weixin_38740144-15209420-4744300845399269797.pdf-第3页.png

第3页 / 共7页

weixin_38740144-15209420-4744300845399269797.pdf-第4页.png

第4页 / 共7页

weixin_38740144-15209420-4744300845399269797.pdf-第5页.png

第5页 / 共7页

weixin_38740144-15209420-4744300845399269797.pdf-第6页.png

第6页 / 共7页

weixin_38740144-15209420-4744300845399269797.pdf-第7页.png

第7页 / 共7页

文本预览

第２８卷　第４期２００８年４月光　学　学　报犃犆犜犃犗犘犜犐犆犃犛犐犖犐犆犃Ｖｏｌ．２８，Ｎｏ．４犃狆狉犻犾，２００８文章编号：０２５３２２３９（２００８）０４０７１５０７小波变换轮廓术中用小波脊系数幅值引导相位展开的研究李思坤　陈文静　苏显渝（四川大学电子信息学院，四川成都６１００６４）摘要　为了减少小波变换轮廓术中相位展开过程的误差传递，从小波变换的相关实质出发，提出了在小波变换轮廓术中利用以前被忽略的小波脊系数幅值作为可靠度判据指导相位展开的方法。该方法选择最大幅值的小波脊系数所在位置作为相位展开起始点，根据小波脊系数幅值的大小，确定一条由大幅值到小幅值的最优化的展开路径，最大限度减少了相位展开过程中的误差传递。由于充分利用了小波变换系数的幅值信息，最大限度减小了相位展开过程中的误差传递。计算机模拟和实验验证了基于小波脊系数幅值的相位展开方法的正确性。关键词　光学测量；相位展开；小波变换轮廓术；小波脊；条纹分析中图分类号　Ｏ４３８．２　　　文献标识码　Ａ犘犺犪狊犲犝狀狑狉犪狆狆犻狀犵犌狌犻犱犲犱犫狔犃犿狆犾犻狋狌犱犲狅犳犠犪狏犲犾犲狋犚犻犱犵犲犆狅犲犳犳犻犮犻犲狀狋狊犻狀犠犪狏犲犾犲狋犜狉犪狀狊犳狅狉犿犘狉狅犳犻犾狅犿犲狋狉狔犔犻犛犻犽狌狀　犆犺犲狀犠犲狀犼犻狀犵　犛狌犡犻犪狀狔狌（犛犮犺狅狅犾狅犳犈犾犲犮狋狉狅狀犻犮犪狀犱犐狀犳狅狉犿犪狋犻狅狀犈狀犵犻狀犲犲狉犻狀犵，犛犻犮犺狌犪狀犝狀犻狏犲狉狊犻狋狔，犆犺犲狀犵犱狌，犛犻犮犺狌犪狀６１００６４，犆犺犻狀犪）犃犫狊狋狉犪犮狋　犐狀狅狉犱犲狉狋狅犾犻犿犻狋狋犺犲犲狉狉狅狉狋狉犪狀犳犲狉犻狀狑犪狏犲犾犲狋狋狉犪狀狊犳狉狅犿狆狉狅犳犻犾狅犿犲狋狉狔，狑犲狆狉狅狆狅狊犲犪狀犻犱犲犪狋犺犪狋狋犺犲犪犿狆犾犻狋狌犱犲狏犪犾狌犲狊狅犳狑犪狏犲犾犲狋狋狉犪狀狊犳狅狉犿犮狅犲犳犳犻犮犻犲狀狋狊犪狋狑犪狏犲犾犲狋狉犻犱犵犲狆狅狊犻狋犻狅狀，狑犺犻犮犺犺犪狊犫犲犲狀犻犵狀狅狉犲犱犫犲犳狅狉犲，犮犪狀犫犲狌狊犲犱狋狅犵狌犻犱犲狋犺犲狆犺犪狊犲狌狀狑狉犪狆狆犻狀犵．犐狋犿犲犪狀狊狋犺犪狋狋犺犲狑狉犪狆狆犲犱狆犺犪狊犲犾狅犮犪狋犲犱犪狋狋犺犲狆犻狓犲犾狑犻狋犺犺犻犵犺犲狊狋犪犿狆犾犻狋狌犱犲狏犪犾狌犲狑犻犾犾犫犲狊犲犾犲犮狋犲犱犪狊狋犺犲狊狋犪狉狋犻狀犵狆狅犻狀狋狅犳狋犺犲狆犺犪狊犲狌狀狑狉犪狆狆犻狀犵，犪狀犱狋犺犲狀狋犺犲狆犻狓犲犾狑犻狋犺犺犻犵犺犲狉犪犿狆犾犻狋狌犱犲狏犪犾狌犲狑犻犾犾犫犲狌狀狑狉犪狆狆犲犱犲犪狉犾犻犲狉．犛狅狋犺犲狆犪狋犺狅犳狆犺犪狊犲狌狀狑狉犪狆狆犻狀犵犻狊犪犾狑犪狔狊犪犾狅狀犵狋犺犲犱犻狉犲犮狋犻狅狀犳狉狅犿狋犺犲狆犻狓犲犾狑犻狋犺犺犻犵犺犲狉犪犿狆犾犻狋狌犱犲狏犪犾狌犲狋狅狋犺犲狅狀犲狑犻狋犺犾狅狑犲狉犪犿狆犾犻狋狌犱犲狏犪犾狌犲．犅犲犮犪狌狊犲狅犳犿犪犽犻狀犵犳狌犾犾狌狊犲狅犳狋犺犲犪犿狆犾犻狋狌犱犲犻狀犳狅狉犿犪狋犻狅狀狅犳狑犪狏犲犾犲狋犮狅犲犳犳犻犮犻犲狀狋狊犪狋狑犪狏犲犾犲狋狉犻犱犵犲狆狅狊犻狋犻狅狀，狋犺犲犲狉狉狅狉狋狉犪狀狊犳犲狉犻狊犾犻犿犻狋犲犱狑犻狋犺犻狀犾狅犮犪犾犿犻狀犻犿狌犿犪狉犲犪狊犱狌狉犻狀犵狋犺犲狆狉狅犮犲狊狊狅犳狆犺犪狊犲狌狀狑狉犪狆狆犻狀犵．犆狅犿狆狌狋犲狉狊犻犿狌犾犪狋犻狅狀犪狀犱犲狓狆犲狉犻犿犲狀狋犪犾狉犲狊狌犾狋狏犲狉犻犳狔狋犺犲狆狉狅狆狅狊犲犱犻犱犲犪．犓犲狔狑狅狉犱狊　狅狆狋犻犮犪犾犿犲犪狊狌狉犲犿犲狀狋；狆犺犪狊犲狌狀狑狉犪狆狆犻狀犵；狑犪狏犲犾犲狋狋狉犪狀狊犳狅狉犿狆狉狅犳犻犾狅犿犲狋狉狔；狑犪狏犲犾犲狋狉犻犱犵犲；犳狉犻狀犵犲犪狀犪犾狔狊犻狊１　引　　言光学三维传感具有非接触、精度高、测量速度快、自动化程度高等优点，广泛地应用在机器视觉、自动加工、工业自动检测、产品质量控制、实物仿型、生物医学等领域。基于相位测量的光学三维传感方法最后都是通过计算反正切函数得到相位值，因此相位值分布在（－π，π）之间，呈现锯齿状不连续分布，被称为相位截断。为了从相位中计算被测物体的高度分布，必须将由于反正切函数运算引起的截断相位恢复成原有的连续相位，这一过程称为相位展开。相位展开是光学三维传感的一个关键技术，国内外学者对此进行了大量研究工作，取得了很多成果［１～４］。近年来，小波变换被引入基于结构光照明的光学三维轮廓测量中，出现了小波测量轮廓术［５］和采用小波方法消除无效信息的方法［６，７］。在小波测量　　收稿日期：２００７０８０７；收到修改稿日期：２００７１０２９基金项目：国家自然科学基金（６０６７７０２８）资助课题。作者简介：李思坤（１９８２－），男，山东人，硕士研究生，主要从事三维面形测量方面的研究。Ｅｍａｉｌ：ｌｉｓｋ０４０９＠１２６．ｃｏｍ导师简介：陈文静（１９６８－），女，四川人，教授，硕士生导师，主要从事光信息处理、三维测量等方面的研究。Ｅｍａｉｌ：ｃｈｅｎｗｊ０４０９＠１６３．ｃｏｍ

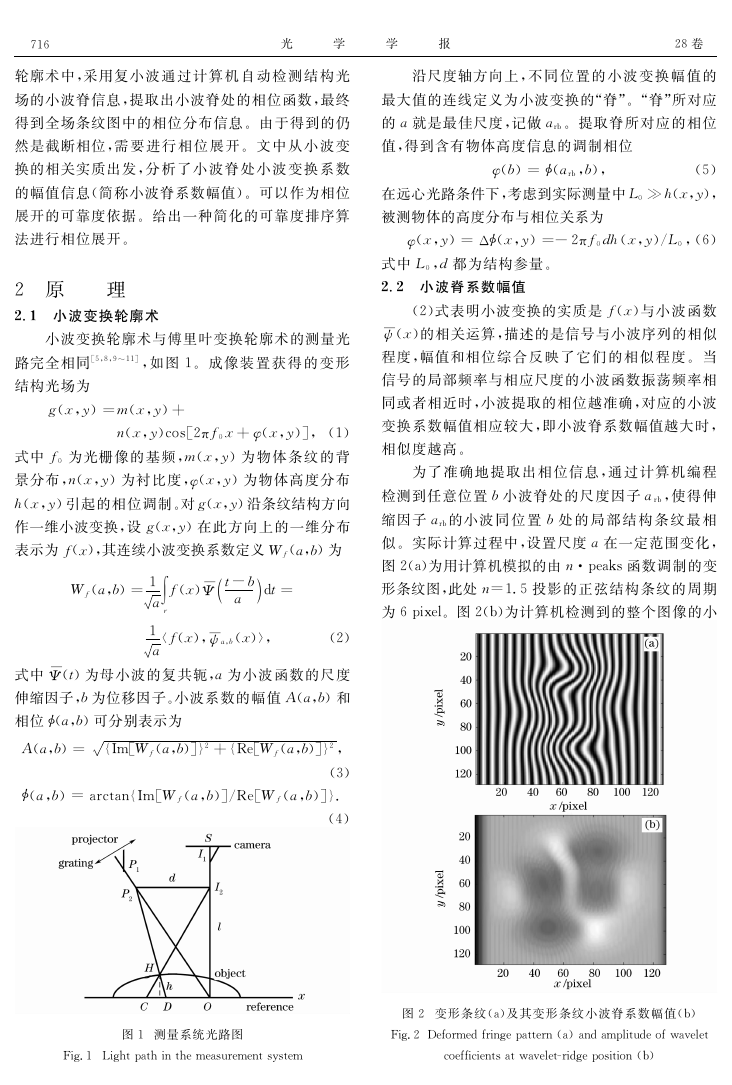
６１７光　　　学　　　学　　　报２８卷轮廓术中，采用复小波通过计算机自动检测结构光场的小波脊信息，提取出小波脊处的相位函数，最终得到全场条纹图中的相位分布信息。由于得到的仍然是截断相位，需要进行相位展开。文中从小波变　　沿尺度轴方向上，不同位置的小波变换幅值的最大值的连线定义为小波变换的“脊”。“脊”所对应的犪就是最佳尺度，记做犪ｒｂ。提取脊所对应的相位值，得到含有物体高度信息的调制相位换的相关实质出发，分析了小波脊处小波变换系数的幅值信息（简称小波脊系数幅值）。可以作为相位展开的可靠度依据。给出一种简化的可靠度排序算 φ（犫）＝（犪ｒｂ，犫），（５）在远心光路条件下，考虑到实际测量中犔０ 犺（狓，狔），被测物体的高度分布与相位关系为法进行相位展开。２　原　　理２．１　小波变换轮廓术小波变换轮廓术与傅里叶变换轮廓术的测量光路完全相同［５，８，９～１１］，如图１。成像装置获得的变形结构光场为犵（狓，狔）＝犿（狓，狔）＋狀（狓，狔）ｃｏｓ［２π犳０狓＋φ（狓，狔）］，（１）式中犳０为光栅像的基频，犿（狓，狔）为物体条纹的背景分布，狀（狓，狔）为衬比度，φ（狓，狔）为物体高度分布犺（狓，狔）引起的相位调制。对犵（狓，狔）沿条纹结构方向作一维小波变换，设犵（狓，狔）在此方向上的一维分布表示为犳（狓），其连续小波变换系数定义犠犳（犪，犫）为　犠犳（犪，犫）＝１犳（狓）－ Ψ 槡犪∫ 狉狋－犫（）犪ｄ狋＝ φ（狓，狔）＝ Δ（狓，狔）＝－２π犳０犱犺（狓，狔）／犔０，（６）式中犔０，犱都为结构参量。２．２　小波脊系数幅值（２）式表明小波变换的实质是犳（狓）与小波函数－ ψ（狓）的相关运算，描述的是信号与小波序列的相似程度，幅值和相位综合反映了它们的相似程度。当信号的局部频率与相应尺度的小波函数振荡频率相同或者相近时，小波提取的相位越准确，对应的小波变换系数幅值相应较大，即小波脊系数幅值越大时，相似度越高。为了准确地提取出相位信息，通过计算机编程检测到任意位置犫小波脊处的尺度因子犪ｒｂ，使得伸缩因子犪ｒｂ的小波同位置犫处的局部结构条纹最相似。实际计算过程中，设置尺度犪在一定范围变化，图２（ａ）为用计算机模拟的由狀·ｐｅａｋｓ函数调制的变形条纹图，此处狀＝１．５投影的正弦结构条纹的周期为６ｐｉｘｅｌ。图２（ｂ）为计算机检测到的整个图像的小〈犳（狓），－ ψ犪，犫（狓）〉，１槡犪（２）式中－ Ψ（狋）为母小波的复共轭，犪为小波函数的尺度伸缩因子，犫为位移因子。小波系数的幅值犃（犪，犫）和相位（犪，犫）可分别表示为犃（犪，犫）＝｛Ｉｍ［犠犳（犪，犫）］｝２＋｛Ｒｅ［犠犳（犪，犫）］｝２，槡（３） （犪，犫）＝ａｒｃｔａｎ｛Ｉｍ［犠犳（犪，犫）］／Ｒｅ［犠犳（犪，犫）］｝．（４）图１测量系统光路图Ｆｉｇ．２Ｄｅｆｏｒｍｅｄｆｒｉｎｇｅｐａｔｔｅｒｎ（ａ）ａｎｄａｍｐｌｉｔｕｄｅｏｆｗａｖｅｌｅｔＦｉｇ．１Ｌｉｇｈｔｐａｔｈｉｎｔｈｅｍｅａｓｕｒｅｍｅｎｔｓｙｓｔｅｍｃｏｅｆｆｉｃｉｅｎｔｓａｔｗａｖｅｌｅｔｒｉｄｇｅｐｏｓｉｔｉｏｎ（ｂ）图２变形条纹（ａ）及其变形条纹小波脊系数幅值（ｂ）

４期李思坤等：　小波变换轮廓术中用小波脊系数幅值引导相位展开的研究７１７波脊系数的幅值分布图，它反映了小波和局部条纹的相似程度。此处，犪的取值范围为［１，１０］，犪取０．５。［５］对比观察图２（ａ）、图２（ｂ）可见，由于犪ｒ犫＝１／犳犫（犳犫为位置犫处的局部频率），对应变形条纹图中较宽的部分，局部频率较小，犪ｒ犫相对较大，小波脊系数幅值较大；变形条纹中较窄的部分，局部频率较大，犪ｒ犫相对较小，小波脊系数幅值较小。因为在不存在阴影和条纹断裂时，准确的犪值在［犪－犪，犪＋犪］之间，犪的值可能存在±犪／２的误差量，它对低频率的条纹部分的小波脊系数幅值影响较小，相位提取的准确度相对较大（如图２（犫）对应部分较明亮），对较高频率部分的小波脊系数幅值影响较大［如图２（ａ）所示］，相位提取准确度相对较低［如图２（ｂ）对应部分较暗］。此外，如果条纹中存在阴影和条纹断裂时，小波和局部条纹的相似度小，小波脊系数幅值小。可见小波脊系数幅值可以作为一个可靠度判据，用来指导相位展开。２．３　相位展开方法及算法在相位展开过程中，对小波脊系数幅值从大到小排序，从幅值最大处开始进行，选择一条沿着幅值最大的相位展开路径，减少了误差传递，提高了相位展开的准确度。传统的可靠度排序的相位展开算法［１，２］需要一个队列犙存放依次排列的未展开点的犃（犪，犫）；每展开一个点，都要将该点周围未展开的点送入队列，进行排序，在Ｍａｔｌａｂ计算机语言平台上，非常费时。本文在此基础上进行改进。基于滤波思想，首先设置一个与小波脊系数幅值矩阵和截断相位矩阵等大小的二进制矩阵犖（犖中元素的坐标和前两者对应相同），犖的元素值预先设定为０，根据展开过程，犖的值动态发生改变。用犖将参加排序的点滤出，即将犖与小波脊系数模值矩阵相乘，检测出滤出点中最大值的坐标，即为参加排序点中小波脊系数模值最大值点的坐标，从而得到即将进行相位展开的点的坐标。此外，还需要设置一个二进制模板Ｍ用于标记已展开点，该模板的值预先设为０，表示相位尚未展开，每展开一个点，将它在模板上的值置为１。具体步骤如下：１）首先找到小波脊系数幅值犃（犪，犫）最大值点。将此点作为相位展开的起始点，在二进制模板Ｍ上将与该点对应的点标记为已展开（值为１），在犖中找出与之对应的点，并将与之相邻的４个元素的值设置为１。如图３（ａ）所示。图３用小波脊系数幅值引导相位展开方法算法。（ａ）第一步，（ｂ）第二步，（ｃ）第三步Ｆｉｇ．３Ｐｈａｓｅｕｎｗｒａｐｐｉｎｇａｌｇｏｒｉｔｈｍｇｕｉｄｅｄｂｙａｍｐｌｉｔｕｄｅｏｆｗａｖｅｌｅｔｃｏｅｆｆｉｃｉｅｎｔｓａｔｗａｖｅｌｅｔｒｉｄｇｅｐｏｓｉｔｉｏｎ．（ａ）Ｓｔｅｐ１，（ｂ）ｓｔｅｐ２，（ｃ）ｓｔｅｐ３

８１７光　　　学　　　学　　　报２８卷　　２）用二进制矩阵犖乘以犃（犪，犫），滤出犃（犪，犫）中已展开点的邻点，找出滤出点中最大值的坐标，完为８．１０ｍｍ，图像的尺寸为１２８ｐｉｘｅｌ×１２８ｐｉｘｅｌ。为不失一般性，分别模拟了变形条纹中存在局部阴成截断相位矩阵中已展开的起始点与该坐标点间的相位展开，即当该点与起始点相位之差大于 π 时，该点相位值减去２π，相位之差小于－π 时加上２π，直到二者相位差的绝对值小于 π。将该点在模板Ｍ上的对应点标记为已展开。然后在犖矩阵中将与该点相邻的未展开点（模板值为０）的值设为１，并将刚才展开过点的值置为０，如图３（ｂ）所示。３）重复步骤２），如图３（ｃ）所示。当模板标记全影的情况和物体表面存在狭缝引起变形条纹局部断裂的情况。对于存在局部阴影的情况，模拟物体高度为犺＝３．５ｐｅａｋｓ，如图４（ａ）所示，变形条纹如图４（ｂ）所示。小波变换轮廓术提取出截断相位，由于阴影的存在引起局部相位提取不可靠，无法正确地恢复物体面形。图５（ａ）和图５（ｂ）分别为用传统的相位展开方法进行相位展开后恢复的物体面形及对应的误为１时，表示所有点已经展开，结束该算法。差分布，由于阴影的存在引起相位展开过程中误差的３　模拟及实验采用计算机模拟和实验来验证所提出的方法在相位展开中的作用。模拟系统结构参量为犔０／犱＝１，模拟的被测物体由Ｍａｔｌａｂ函数库中提供的ｐｅａｋｓ函数表示（高度可调以满足不同的模拟的要求），设置犺＝狀·ｐｅａｋｓ。当狀＝１时，其最大的高度传递（常称为拉线误差），不能正确地恢复物体面形。图６（ａ）为小波脊系数幅值的分布图，图６（ｂ）、图６（ｃ）为小波脊系数幅值指导相位展开方法进行相位展开后恢复的物体面形及对应的误差分布。与用传统相位展开方法进行相位展开恢复的物体面形相比，其误差被限制在了很小的区域内部。图４存在局部阴影时模拟物体（ａ）及其变形条纹（ｂ）Ｆｉｇ．４Ｓｉｍｕｌａｔｅｄｏｂｊｅｃｔ（ａ）ａｎｄｄｅｆｏｒｍｅｄｆｒｉｎｇｅｐａｔｔｅｒｎ（ｂ）ｗｉｔｈｌｏｃａｌｓｈａｄｏｗ图５存在局部阴影时传统相位展开方法恢复的物体面形（ａ）及误差分布（ｂ）Ｆｉｇ．５Ｒｅｓｔｏｒｅｄｏｂｊｅｃｔ（ａ）ａｎｄｅｒｒｏｒｄｉｓｔｒｉｂｕｔｉｏｎ（ｂ）ｕｓｉｎｇｔｒａｄｉｔｉｏｎａｌｐｈａｓｅｕｎｗｒａｐｐｉｎｇａｌｇｏｒｉｔｈｍｗｉｔｈｌｏｃａｌｓｈａｄｏｗ　　对于存在局部条纹断裂的情况，模拟的物体如图７（ａ）所示，物体表面存在狭缝，引起变形条纹对应狭缝区域出现断裂，如图７（ｂ）所示。用小波变换轮廓术提取出截断相位，条纹断裂的存在引起局部相位提取不可靠，无法正确地恢复物体面形。图８（ａ）和图８（ｂ）分别为传统相位展开方法进行相位展开后恢

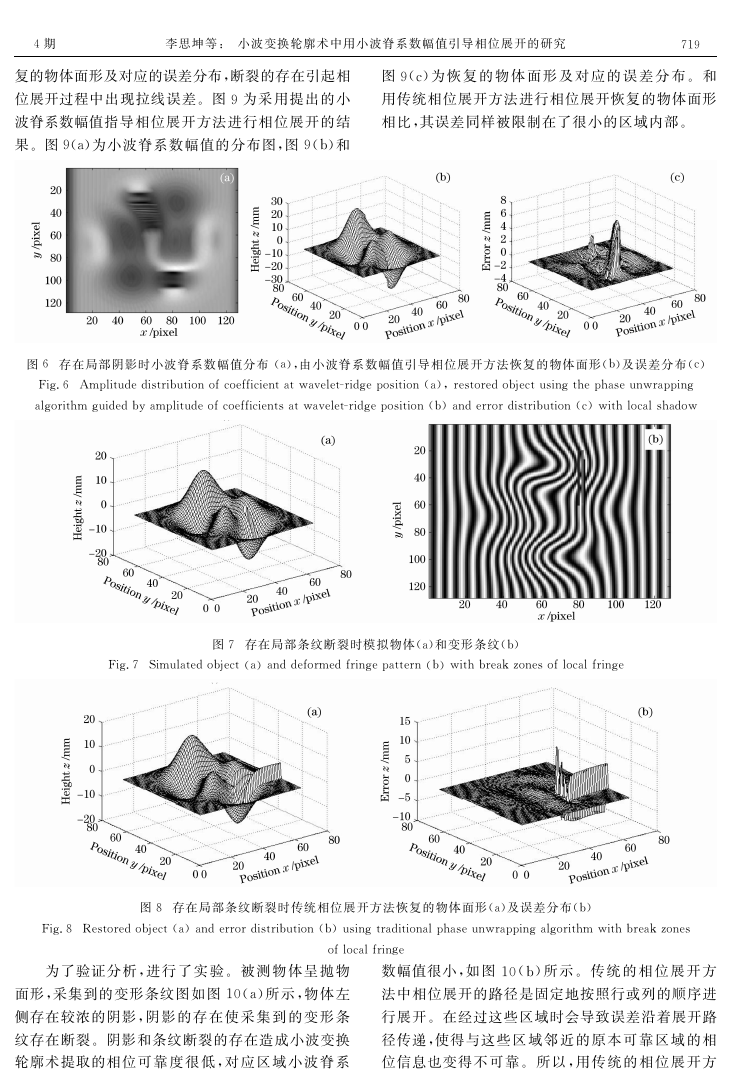
４期李思坤等：　小波变换轮廓术中用小波脊系数幅值引导相位展开的研究９１７复的物体面形及对应的误差分布，断裂的存在引起相位展开过程中出现拉线误差。图９为采用提出的小波脊系数幅值指导相位展开方法进行相位展开的结果。图９（ａ）为小波脊系数幅值的分布图，图９（ｂ）和图９（ｃ）为恢复的物体面形及对应的误差分布。和用传统相位展开方法进行相位展开恢复的物体面形相比，其误差同样被限制在了很小的区域内部。图６存在局部阴影时小波脊系数幅值分布（ａ），由小波脊系数幅值引导相位展开方法恢复的物体面形（ｂ）及误差分布（ｃ）Ｆｉｇ．６Ａｍｐｌｉｔｕｄｅｄｉｓｔｒｉｂｕｔｉｏｎｏｆｃｏｅｆｆｉｃｉｅｎｔａｔｗａｖｅｌｅｔｒｉｄｇｅｐｏｓｉｔｉｏｎ（ａ），ｒｅｓｔｏｒｅｄｏｂｊｅｃｔｕｓｉｎｇｔｈｅｐｈａｓｅｕｎｗｒａｐｐｉｎｇａｌｇｏｒｉｔｈｍｇｕｉｄｅｄｂｙａｍｐｌｉｔｕｄｅｏｆｃｏｅｆｆｉｃｉｅｎｔｓａｔｗａｖｅｌｅｔｒｉｄｇｅｐｏｓｉｔｉｏｎ（ｂ）ａｎｄｅｒｒｏｒｄｉｓｔｒｉｂｕｔｉｏｎ（ｃ）ｗｉｔｈｌｏｃａｌｓｈａｄｏｗ图７存在局部条纹断裂时模拟物体（ａ）和变形条纹（ｂ）Ｆｉｇ．７Ｓｉｍｕｌａｔｅｄｏｂｊｅｃｔ（ａ）ａｎｄｄｅｆｏｒｍｅｄｆｒｉｎｇｅｐａｔｔｅｒｎ（ｂ）ｗｉｔｈｂｒｅａｋｚｏｎｅｓｏｆｌｏｃａｌｆｒｉｎｇｅ图８存在局部条纹断裂时传统相位展开方法恢复的物体面形（ａ）及误差分布（ｂ）Ｆｉｇ．８Ｒｅｓｔｏｒｅｄｏｂｊｅｃｔ（ａ）ａｎｄｅｒｒｏｒｄｉｓｔｒｉｂｕｔｉｏｎ（ｂ）ｕｓｉｎｇｔｒａｄｉｔｉｏｎａｌｐｈａｓｅｕｎｗｒａｐｐｉｎｇａｌｇｏｒｉｔｈｍｗｉｔｈｂｒｅａｋｚｏｎｅｓｏｆｌｏｃａｌｆｒｉｎｇｅ　　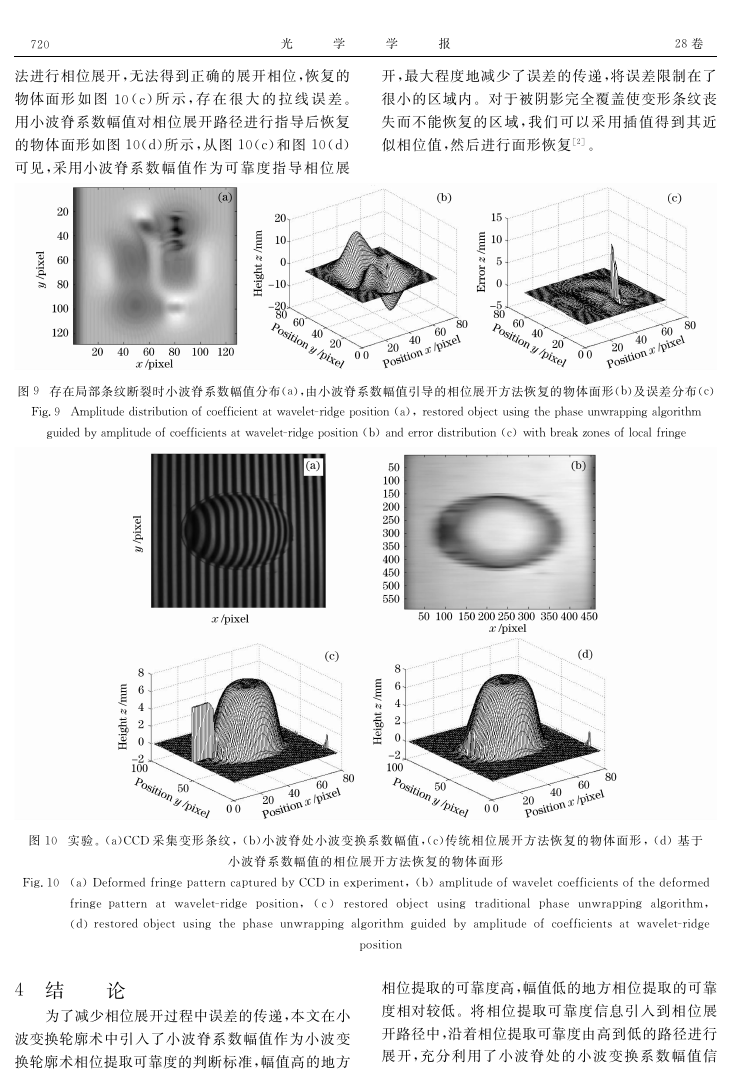为了验证分析，进行了实验。被测物体呈抛物面形，采集到的变形条纹图如图１０（ａ）所示，物体左侧存在较浓的阴影，阴影的存在使采集到的变形条数幅值很小，如图１０（ｂ）所示。传统的相位展开方法中相位展开的路径是固定地按照行或列的顺序进行展开。在经过这些区域时会导致误差沿着展开路纹存在断裂。阴影和条纹断裂的存在造成小波变换径传递，使得与这些区域邻近的原本可靠区域的相轮廓术提取的相位可靠度很低，对应区域小波脊系位信息也变得不可靠。所以，用传统的相位展开方

０２７光　　　学　　　学　　　报２８卷法进行相位展开，无法得到正确的展开相位，恢复的开，最大程度地减少了误差的传递，将误差限制在了物体面形如图１０（ｃ）所示，存在很大的拉线误差。用小波脊系数幅值对相位展开路径进行指导后恢复很小的区域内。对于被阴影完全覆盖使变形条纹丧失而不能恢复的区域，我们可以采用插值得到其近的物体面形如图１０（ｄ）所示，从图１０（ｃ）和图１０（ｄ）可见，采用小波脊系数幅值作为可靠度指导相位展似相位值，然后进行面形恢复［２］。图９存在局部条纹断裂时小波脊系数幅值分布（ａ），由小波脊系数幅值引导的相位展开方法恢复的物体面形（ｂ）及误差分布（ｃ）Ｆｉｇ．９Ａｍｐｌｉｔｕｄｅｄｉｓｔｒｉｂｕｔｉｏｎｏｆｃｏｅｆｆｉｃｉｅｎｔａｔｗａｖｅｌｅｔｒｉｄｇｅｐｏｓｉｔｉｏｎ（ａ），ｒｅｓｔｏｒｅｄｏｂｊｅｃｔｕｓｉｎｇｔｈｅｐｈａｓｅｕｎｗｒａｐｐｉｎｇａｌｇｏｒｉｔｈｍｇｕｉｄｅｄｂｙａｍｐｌｉｔｕｄｅｏｆｃｏｅｆｆｉｃｉｅｎｔｓａｔｗａｖｅｌｅｔｒｉｄｇｅｐｏｓｉｔｉｏｎ（ｂ）ａｎｄｅｒｒｏｒｄｉｓｔｒｉｂｕｔｉｏｎ（ｃ）ｗｉｔｈｂｒｅａｋｚｏｎｅｓｏｆｌｏｃａｌｆｒｉｎｇｅ图１０实验。（ａ）ＣＣＤ采集变形条纹，（ｂ）小波脊处小波变换系数幅值，（ｃ）传统相位展开方法恢复的物体面形，（ｄ）基于小波脊系数幅值的相位展开方法恢复的物体面形Ｆｉｇ．１０（ａ）ＤｅｆｏｒｍｅｄｆｒｉｎｇｅｐａｔｔｅｒｎｃａｐｔｕｒｅｄｂｙＣＣＤｉｎｅｘｐｅｒｉｍｅｎｔ，（ｂ）ａｍｐｌｉｔｕｄｅｏｆｗａｖｅｌｅｔｃｏｅｆｆｉｃｉｅｎｔｓｏｆｔｈｅｄｅｆｏｒｍｅｄｆｒｉｎｇｅｐａｔｔｅｒｎａｔｗａｖｅｌｅｔｒｉｄｇｅｐｏｓｉｔｉｏｎ，（ｃ）ｒｅｓｔｏｒｅｄｏｂｊｅｃｔｕｓｉｎｇｔｒａｄｉｔｉｏｎａｌｐｈａｓｅｕｎｗｒａｐｐｉｎｇａｌｇｏｒｉｔｈｍ，（ｄ）ｒｅｓｔｏｒｅｄｏｂｊｅｃｔｕｓｉｎｇｔｈｅｐｈａｓｅｕｎｗｒａｐｐｉｎｇａｌｇｏｒｉｔｈｍｇｕｉｄｅｄｂｙａｍｐｌｉｔｕｄｅｏｆｃｏｅｆｆｉｃｉｅｎｔｓａｔｗａｖｅｌｅｔｒｉｄｇｅ　　　　　　　　　　　　　　　　　　　　　　ｐｏｓｉｔｉｏｎ４　结　　论为了减少相位展开过程中误差的传递，本文在小波变换轮廓术中引入了小波脊系数幅值作为小波变换轮廓术相位提取可靠度的判断标准，幅值高的地方相位提取的可靠度高，幅值低的地方相位提取的可靠度相对较低。将相位提取可靠度信息引入到相位展开路径中，沿着相位提取可靠度由高到低的路径进行展开，充分利用了小波脊处的小波变换系数幅值信

４期李思坤等：　小波变换轮廓术中用小波脊系数幅值引导相位展开的研究１２７息，使得相位提取可靠度高的地方首先展开，相位提取可靠度低的地方集中到最后展开。与传统的相位ｄｅｍｏｄｕｌａｔｉｏｎｔｅｃｈｎｉｑｕｅｂａｓｅｄｏｎｗａｖｅｌｅｔｔｒａｎｓｆｏｒｍ［Ｊ］．犃犮狋犪犗狆狋犻犮犪犛犻狀犻犮犪，２０００，２０（１２）：１６１７～１６２２　许庆红，钟约先，由志福．基于小波变换的解相技术研究［Ｊ］．光展开方法相比，利用小波脊系数幅值引导相位展开的学学报，２０００，２０（１２）：１６１７～１６２２方法能够很好地解决小波变换轮廓术中相位展开的误差传递问题，体现出了较高的优越性。参考文献１ＸｉａｎｙｕＳｕ，ＷｅｎｊｉｎｇＣｈｅｎ．Ｒｅｌｉａｂｉｌｉｔｙｇｕｉｄｅｄｐｈａｓｅｕｎｗｒａｐｐｉｎｇａｌｇｏｒｉｔｈｍ：ａｒｅｖｉｅｗ［Ｊ］．犗狆犻狋犮狊犪狀犱犔犪狊犲狉狊犻狀犈狀犵犻狀犲犲狉犻狀犵，２００４，４２（３）：２４５～２６１２Ｓｕｘｉａｎｙｕ，Ｔａｎｓｏｎｇｘｉｎ，Ｘｉａｎｇｌｉｑｕｎ犲狋犪犾．．ＣｏｍｐｌｅｘｏｂｊｅｃｔｓｈａｐｅｍｅａｓｕｒｅｍｅｎｔｕｓｉｎｇＦＴＰｍｅｔｈｏｄ［Ｊ］．犃犮狋犪犗狆狋犻犮犪犛犻狀犻犮犪，１９９８，１８（９）：１２２６～１２３３　苏显渝，谭松新，向立群等．基于傅里叶变换轮廓术方法的复杂物体三维面形测量［Ｊ］．光学学报，１９９８，１８（９）：１２２６～１２３３３Ｍ．Ｔａｋｅｄａ，Ｔ．Ａｂｅ．Ｐｈａｓｅｕｎｗｒａｐｐｉｎｇｂｙａｍａｘｉｍｕｍｃｒｏｓｓ ａｍｐｌｉｔｕｄｅｓｐａｎｎｉｎｇｔｒｅｅａｌｇｏｒｉｔｈｍ：ａｃｏｍｐａｒａｔｉｖｅｓｔｕｄｙ［Ｊ］．犗狆狋．犈狀犵狀犵．，１９９６，３５（８）：２３４５～２３５１４Ｄ．Ｃ．Ｇｈｉｇｌｉａ，Ｇ．Ａ．Ｍａｓｔｉｎ，Ｌ．Ａ．Ｒｏｍｅｒｏ．Ｃｅｌｌｕｌａｒ ａｕｔｏｍａｔａｍｅｔｈｏｄｆｏｒｐｈａｓｅｕｎｗｒａｐｐｉｎｇ［Ｊ］．犑．犗狆狋．犛狅犮．犃犿．犃，ｌ９８７，４（１）：２６７～１８０５ＪｉｎｇａｎｇＺｈｏｎｇ，ＪｉａｗｅｎＷｅｎｇ．Ｓｐａｔｉａｌｃａｒｒｉｅｒｆｒｉｎｇｅｐａｔｔｅｒｎａｎａｌｙｓｉｓｂｙｍｅａｎｓｏｆｗａｖｅｌｅｔｔｒａｎｓｆｏｒｍ：ｗａｖｅｌｅｔｔｒａｎｓｆｏｒｍｐｒｏｆｉｌｏｍｅｔｒｙ［Ｊ］．犃狆狆犾．犗狆狋．，２００４，４３（２６）：４９９３～４９９８６ＸｕＱｉｎｇｈｏｎｇ，ＺｈｏｎｇＹｕｅｘｉａｎ，ＹｏｕＺｈｉｆｕ．Ｓｔｕｄｙｏｎｐｈａｓｅ７ＦｕＳｈｕａｎｇ，ＷａｎｇＹｕｎｓｈａｎ，ＨａｎＧｕａｎｇｂｉｎｇ犲狋犪犾．．Ｆｏｕｒｉｅｒｔｒａｎｓｆｏｒｍｐｒｏｆｉｌｏｍｅｔｒｙｉｎ３Ｄｍｅａｓｕｒｅｍｅｎｔｂａｓｅｄｏｎｗａｖｅｌｅｔｄｉｇｉｔａｌｆｉｌｔｅｒ［Ｊ］．犑．犗狆狋狅犲犾犲犮狋狉狅狀犻犮狊·犔犪狊犲狉，２００４，１５（２）：２０５～２０７　傅　爽，王蕴珊，韩广兵等．基于小波数字滤波的傅里叶变换轮廓法［Ｊ］．光电子·激光，２００４，１５（２）：２０５～２０７８ＳｕｎＪｕａｎ，ＣｈｅｎＷｅｎｊｉｎｇ，ＳｕＸｉａｎｙｕ犲狋犪犾．．Ｓｔｕｄｙｔｈｅｍｅａｓｕｒｅｍｅｎｔｒａｎｇｅｏｆｗａｖｅｌｅｔｔｒａｎｓｆｏｒｍｐｒｏｆｉｌｏｍｅｔｒｙ［Ｊ］．犃犮狋犪犗狆狋犻犮犪犛犻狀犻犮犪，２００７，２７（４）：６４７～６５３　孙　娟，陈文静，苏显渝等．小波变换轮廓术的测量范围研究［Ｊ］．光学学报，２００７，２７（４）：６４７～６５３９Ｍ．Ｔａｋｅｄａ，Ｋ．Ｍｕｔｏｈ．Ｆｏｕｒｉｅｒｔｒａｎｓｆｏｒｍｐｒｏｆｉｌｏｍｅｔｒｙｆｏｒｔｈｅａｕｔｏｍａｔｉｃｍｅａｓｕｒｅｍｅｎｔ３Ｄｏｂｊｅｃｔｓｈａｐｅｓ［Ｊ］．犃狆狆犾．犗狆狋．，１９８３，２２（２４）：３９７７～３９８２１０ＭａｏＸｉａｎｆｕ，ＣｈｅｎＷｅｎｊｉｎｇ，ＳｕＸｉａｎｙｕ．ＡｎａｌｙｓｉｓｏｎａｎｉｍｐｒｏｖｅｄＦｏｕｒｉｅｒｔｒａｎｓｆｏｒｍｐｒｏｆｉｌｏｍｅｔｒｙ［Ｊ］．犆犺犻狀．犑．犔犪狊犲狉狊，２００７，３４（１）：９７～１０２　毛先富，陈文静，苏显渝．傅里叶变换轮廓术新理论研究［Ｊ］．中国激光，２００７，３４（１）：９７～１０２１１ＷｅｎｇＪｉａｗｅｎ，ＺｈｏｎｇＪｉｎｇａｎｇ．Ａｐｐｌｙｗａｖｅｌｅｔｔｒａｎｓｆｏｒｍｔｏｐｈａｓｅａｎａｌｙｓｉｓｏｆｓｐａｔｉａｌｃａｒｒｉｅｒｆｒｉｎｇｅｐａｔｔｅｒｎ［Ｊ］．犃犮狋犪犗狆狋犻犮犪犛犻狀犻犮犪，２００５，２５（４）：４５４～４５９　翁嘉文，钟金钢．小波变换在载频条纹相位分析法中的应用研究［Ｊ］．光学学报，２００５，２５（４）：４５４～４５９

分享到：

赞收藏

资料库

小波变换轮廓术中用小波脊系数幅值引导相位展开的研究.pdf

相关推荐

开发技术

热门标签

最新资料