UMAT经验及示例.pdf-资料库

1、为何需要使用用户材料子程序（User-Defined Material, UMAT）？很简单，当 ABAQUS 没有提供我们需要的材料模型时。所以，在决定自己定义一种新的材料模型之前，最好对 ABAQUS 已经提供的模型心中有数，并且尽量使用现有的模型，因为这些模型已经经过详细的验证，并被广泛接受。 UMAT 子程序具有强大的功能，使用 UMAT 子程序： (1)可以定义材料的本构关系，使用 ABAQUS 材料库中没有包含的材料进行计算，扩充程序功能。 (2) 几乎可以用于力学行为分析的任何分析过程，几乎可以把用户材料属性赋予 ABAQU S 中的任何单元。 (3) 必须在 UMAT 中提供材料本构模型的雅可比（Jacobian）矩阵，即应力增量对应变增量的变化率。 (4) 可以和用户子程序“USDFLD”联合使用，通过“USDFLD”重新定义单元每一物质点上传递到 UMAT 中场变量的数值。 2、需要哪些基础知识？先看一下 ABAQUS 手册（ABAQUS Analysis User's Manual）里的一段话： Warning: The use of this option generally requires considerable expertise(一定的专业知识). The user is cautioned that the implementation（实现） of any realistic constitutive（基本） model requires extensive（广泛的） development and testing. Initial testing on a single eleme nt model with prescribed traction loading（指定拉伸载荷） is strongly recommended. 但这并不意味着非力学专业，或者力学基础知识不很丰富者就只能望洋兴叹，因为我们的任务不是开发一套完整的有限元软件，而只是提供一个描述材料力学性能的本构方程（Constitutive equation）而已。当然，最基本的一些概念和知识还是要具备的，比如：应力(stress),应变（strain）及其分量； volumetric part 和 deviatoric part；模量（modul us）、泊松比(Poisson’s ratio)、拉梅常数(Lame constant)；矩阵的加减乘除甚至求逆；还有一些高等数学知识如积分、微分等。 3、UMAT 的基本任务？我们知道，有限元计算（增量方法）的基本问题是：已知第 n 步的结果（应力，应变等） nσ ， nε ，然后给出一个应变增量 1+ndε ，计算新的应力 1+nσ 。UMAT 要完成这一 / 。 σΔ 是应力增量矩阵（张量或计算，并要计算 Jacobian 矩阵 DDSDDE(I,J) = 许更合适）， εΔ 是应变增量矩阵。DDSDDE(I,J) 定义了第 J 个应变分量的微小变化对 εσ Δ∂ Δ∂

第 I 个应力分量带来的变化。该矩阵只影响收敛速度，不影响计算结果的准确性（当然，不收敛自然得不到结果）。 4、怎样建立自己的材料模型？本构方程就是描述材料应力应变（增量）关系的数学公式，不是凭空想象出来的，而是根据实验结果作出的合理归纳。比如对弹性材料，实验发现应力和应变同步线性增长，所以用一个简单的数学公式描述。为了解释弹塑性材料的实验现象，又提出了一些弹塑性模型，并用数学公式表示出来。对各向同性材料（Isotropic material）,经常采用的办法是先研究材料单向应力-应变规律（如单向拉伸、压缩试验），并用一数学公式加以描述，然后把该规律推广到各应力分量。这叫做“泛化“(generalization)。 5、一个完整的例子及解释由于主程序与 UMAT 之间存在数据传递，甚至一些公共变量，因此必须遵循有关 UMAT 的书写格式，UMAT 中常用的变量在文件开头予以定义，通常格式为： SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD, 1 RPL, DDSDDT, DRPLDE, DRPLDT, 2 STRAN, DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME, 3 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT, 4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,KSTEP,KINC) INCLUDE 'ABA_PARAM.INC' CHARACTER*80 CMNAME DIMENSION STRESS(NTENS),STATEV(NSTATV), 1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS), 2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1), 3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3) user coding to define DDSDDE, STRESS, STATEV, SSE, SPD, SCD and, if necessary, RPL, DDSDDT, DRPLDE, DRPLDT, PNEWDT RETURN END

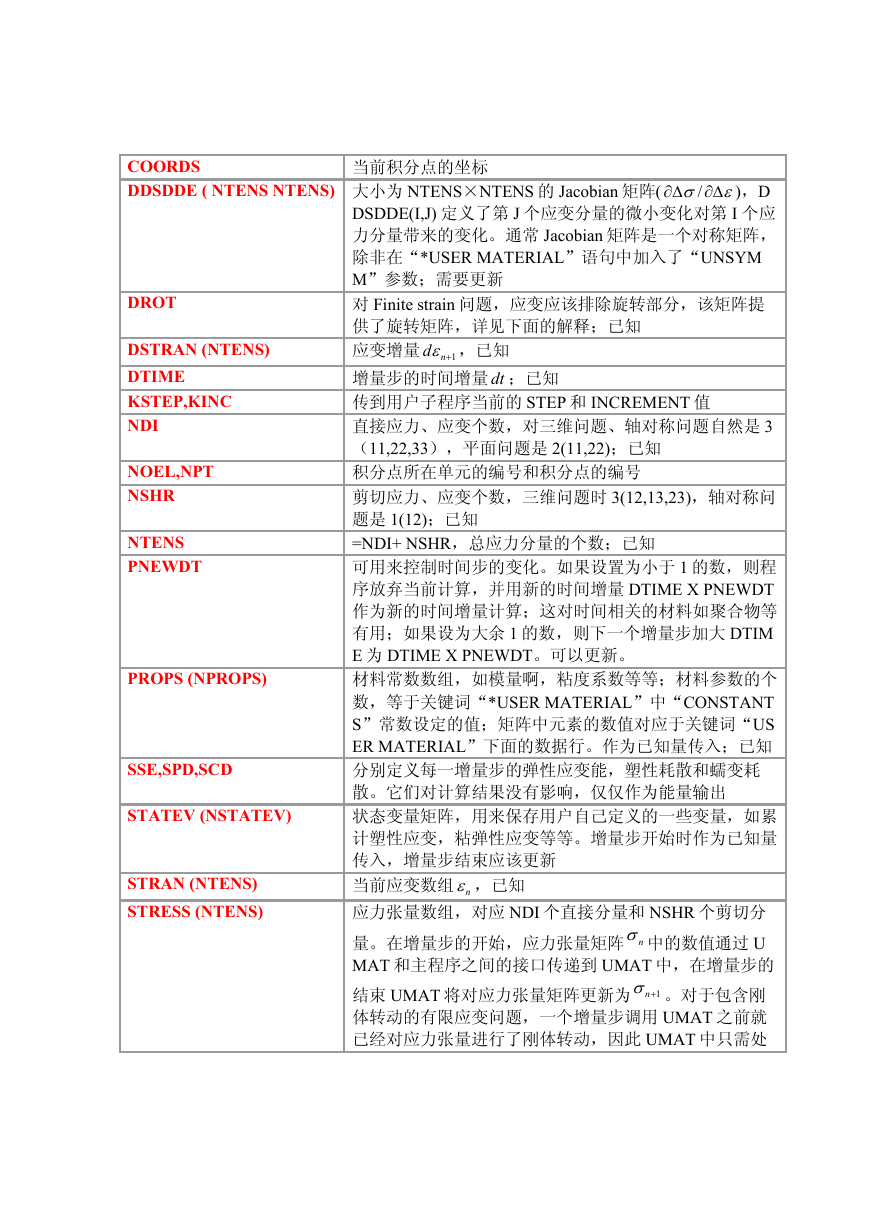
COORDS DDSDDE ( NTENS NTENS) 大小为 NTENS×NTENS 的 Jacobian 矩阵( 当前积分点的坐标 Δ∂ / DROT DSTRAN (NTENS) DTIME KSTEP,KINC NDI NOEL,NPT NSHR NTENS PNEWDT PROPS (NPROPS) SSE,SPD,SCD STATEV (NSTATEV) STRAN (NTENS) STRESS (NTENS) εσ Δ∂ )，D DSDDE(I,J) 定义了第 J 个应变分量的微小变化对第 I 个应力分量带来的变化。通常 Jacobian 矩阵是一个对称矩阵，除非在“*USER MATERIAL”语句中加入了“UNSYM M”参数；需要更新对 Finite strain 问题，应变应该排除旋转部分，该矩阵提供了旋转矩阵，详见下面的解释；已知应变增量 1+ndε ，已知增量步的时间增量 dt ；已知传到用户子程序当前的 STEP 和 INCREMENT 值直接应力、应变个数，对三维问题、轴对称问题自然是 3 （11,22,33），平面问题是 2(11,22)；已知积分点所在单元的编号和积分点的编号剪切应力、应变个数，三维问题时 3(12,13,23)，轴对称问题是 1(12)；已知 =NDI+ NSHR，总应力分量的个数；已知可用来控制时间步的变化。如果设置为小于 1 的数，则程序放弃当前计算，并用新的时间增量 DTIME X PNEWDT 作为新的时间增量计算；这对时间相关的材料如聚合物等有用；如果设为大余 1 的数，则下一个增量步加大 DTIM E 为 DTIME X PNEWDT。可以更新。材料常数数组，如模量啊，粘度系数等等；材料参数的个数，等于关键词“*USER MATERIAL”中“CONSTANT S”常数设定的值；矩阵中元素的数值对应于关键词“US ER MATERIAL”下面的数据行。作为已知量传入；已知分别定义每一增量步的弹性应变能，塑性耗散和蠕变耗散。它们对计算结果没有影响，仅仅作为能量输出状态变量矩阵，用来保存用户自己定义的一些变量，如累计塑性应变，粘弹性应变等等。增量步开始时作为已知量传入，增量步结束应该更新当前应变数组 nε ，已知应力张量数组，对应 NDI 个直接分量和 NSHR 个剪切分量。在增量步的开始，应力张量矩阵 nσ 中的数值通过 U MAT 和主程序之间的接口传递到 UMAT 中，在增量步的结束 UMAT 将对应力张量矩阵更新为 1+nσ 。对于包含刚体转动的有限应变问题，一个增量步调用 UMAT 之前就已经对应力张量进行了刚体转动，因此 UMAT 中只需处

理应力张量的共旋部分。UMAT 中应力张量的度量为柯西（真实）应力。下面这个 UMAT 取自 ABAQUS 手册，是一个用于大变形下的弹塑性材料模型，注意的是这里需要了解 J2 理论。 SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,RPL,DDSDDT, 1 DRPLDE,DRPLDT,STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED, 2 CMNAME,NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT, 3 PNEWDT,CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,KSTEP,KINC) C INCLUDE 'ABA_PARAM.INC' 定义了一些相关参数与变量什么，从 ABAQUS 安装目录下的子文件夹“…\site”中可找到 C CHARACTER*8 CMNAME C DIMENSION STRESS(NTENS),STATEV(NSTATV),DDSDDE(NTENS,NTENS), 1 DDSDDT(NTENS)(应变矩阵),DRPLDE(NTENS),STRAN(NTENS),DSTRAN(NTENS) （应变增量矩阵）, 2 PREDEF(1),DPRED(1),PROPS(NPROPS)(材料常数矩),COORDS(3),DROT(3,3)（旋转矩阵）, 3 DFGRD0(3,3),DFGRD1(3,3) 声明矩阵的尺寸 C C LOCAL ARRAYS C ---------------------------------------------------------------- C EELAS - ELASTIC STRAINS C EPLAS - PLASTIC STRAINS C FLOW - DIRECTION OF PLASTIC FLOW C ---------------------------------------------------------------- C 局部变量，用来暂时保存弹性应变、塑性应变分量以及流动方向 DIMENSION EELAS(6),EPLAS(6),FLOW(6) C PARAMETER(ZERO=0.D0,ONE=1.D0,TWO=2.D0,THREE=3.D0,SIX=6.D0,

1 ENUMAX=.4999D0,NEWTON=10,TOLER=1.0D-6) C C ---------------------------------------------------------------- C UMAT FOR ISOTROPIC ELASTICITY AND ISOTROPIC MISES PLASTICITY C CANNOT BE USED FOR PLANE STRESS C ---------------------------------------------------------------- C PROPS(1) - E C PROPS(2) - NU C PROPS(3..) - SYIELD AN HARDENING DATA C CALLS HARDSUB FOR CURVE OF YIELD STRESS VS. PLASTIC STRAIN C ---------------------------------------------------------------- C C ELASTIC PROPERTIES C 获取杨氏模量，泊松比，作为已知量由 PROPS 向量传入 EMOD=PROPS(1) E ENU=PROPS(2) ν EBULK3=EMOD/(ONE-TWO*ENU) 3K = Ek 3 )21( ν− EG2=EMOD/(ONE+ENU) 2G = EG 2 1( ) υ+ EG=EG2/TWO G = EG ) 1(2 υ+ 3( k − G )2 =λ 3 EG3=THREE*EG 3G ELAM=(EBULK3-EG2)/THREE λ DO K1=1,NTENS DO K2=1,NTENS DDSDDE(K1,K2)=ZERO END DO END DO 弹性部分，Jacobian 矩阵很容易计算

J = 2G + λ λλ ⎡ ⎢ 2G + λλ λ ⎢ ⎢ + λ λ λ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ 2G G G G ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ，所以剪切部 u + i,j u ij j,i =γ 注意，在 ABAQUS 中，剪切应变采用工程剪切应变的定义分模量是 G 而不是 2G C Jacobian 矩阵的程序 C ELASTIC STIFFNESS C DO K1=1,NDI DO K2=1,NDI DDSDDE(K2,K1)=ELAM END DO DDSDDE(K1,K1)=EG2+ELAM END DO DO K1=NDI+1,NTENS DDSDDE(K1,K1)=EG END DO C C RECOVER ELASTIC AND PLASTIC STRAINS AND ROTATE FORWARD C ALSO RECOVER EQUIVALENT PLASTIC STRAIN C 读取弹性应变分量，塑性应变分量，并旋转（调用了 ROTSIG），分别保存在 EELAS 和 EPLAS 中； CALL ROTSIG(STATEV( 1),DROT,EELAS,2,NDI,NSHR) CALL ROTSIG(STATEV(NTENS+1),DROT,EPLAS,2,NDI,NSHR) 读取等效塑性应变 EQPLAS=STATEV(1+2*NTENS) 先假设没有发生塑性流动，按完全弹性变形计算试算应力 σ σεJ . Δ=Δ = σ n σ Δ+ n 1 + C

C CALCULATE PREDICTOR STRESS AND ELASTIC STRAIN C DO K1=1,NTENS DO K2=1,NTENS STRESS(K2)=STRESS(K2)+DDSDDE(K2,K1)*DSTRAN(K1) END DO EELAS(K1)=EELAS(K1)+DSTRAN(K1)弹性应变分量 END DO C 计算 Mises 应力 C CALCULATE EQUIVALENT VON MISES STRESS C SMISES=(STRESS(1)-STRESS(2))**2+(STRESS(2)-STRESS(3))**2 1 +(STRESS(3)-STRESS(1))**2 DO K1=NDI+1,NTENS SMISES=SMISES+SIX*STRESS(K1)**2 END DO SMISES=SQRT(SMISES/TWO) C 根据当前等效塑性应变，调用 HARDSUB 得到对应的屈服应力 C GET YIELD STRESS FROM THE SPECIFIED HARDENING CURVE C NVALUE=NPROPS/2-1 CALL HARDSUB(SYIEL0,HARD,EQPLAS,PROPS(3),NVALUE) C C DETERMINE IF ACTIVELY YIELDING C 如果 Mises 应力大余屈服应力，屈服发生，计算流动方向 IF (SMISES.GT.(ONE+TOLER)*SYIEL0) THEN C C ACTIVELY YIELDING C SEPARATE THE HYDROSTATIC FROM THE DEVIATORIC STRESS C CALCULATE THE FLOW DIRECTION C SHYDRO=(STRESS(1)+STRESS(2)+STRESS(3))/THREE DO K1=1,NDI FLOW(K1)=(STRESS(K1)-SHYDRO)/SMISES END DO DO K1=NDI+1,NTENS FLOW(K1)=STRESS(K1)/SMISES

END DO C 根据 J2 理论并应用 Newton-Rampson 方法求得等效塑性应变增量 C SOLVE FOR EQUIVALENT VON MISES STRESS C AND EQUIVALENT PLASTIC STRAIN INCREMENT USING NEWTON ITERATIO N C SYIELD=SYIEL0 DEQPL=ZERO DO KEWTON=1,NEWTON RHS=SMISES-EG3*DEQPL-SYIELD DEQPL=DEQPL+RHS/(EG3+HARD) CALL HARDSUB(SYIELD,HARD,EQPLAS+DEQPL,PROPS(3),NVALUE) IF(ABS(RHS).LT.TOLER*SYIEL0) GOTO 10 END DO C C WRITE WARNING MESSAGE TO THE .MSG FILE C WRITE(7,2) NEWTON 2 FORMAT(//,30X,'***WARNING - PLASTICITY ALGORITHM DID NOT ', 1 'CONVERGE AFTER ',I3,' ITERATIONS') 10 CONTINUE C 更新应力 1+nσ ，应变分量 C UPDATE STRESS, ELASTIC AND PLASTIC STRAINS AND C EQUIVALENT PLASTIC STRAIN C DO K1=1,NDI STRESS(K1)=FLOW(K1)*SYIELD+SHYDRO EPLAS(K1)=EPLAS(K1)+THREE/TWO*FLOW(K1)*DEQPL EELAS(K1)=EELAS(K1)-THREE/TWO*FLOW(K1)*DEQPL END DO DO K1=NDI+1,NTENS STRESS(K1)=FLOW(K1)*SYIELD EPLAS(K1)=EPLAS(K1)+THREE*FLOW(K1)*DEQPL EELAS(K1)=EELAS(K1)-THREE*FLOW(K1)*DEQPL END DO EQPLAS=EQPLAS+DEQPL C

资料库

UMAT经验及示例.pdf

相关推荐

课程资源

热门标签

最新资料