第1页 / 共43页
第2页 / 共43页
第3页 / 共43页
第4页 / 共43页
第5页 / 共43页
第6页 / 共43页
第7页 / 共43页
第8页 / 共43页
中南大学数值计算实践报告.docx
一、题目1：非线性方程求解
1.实验内容
2.算法原理
3.算法流程图
4.程序代码
5.执行结果及结果分析
6.体会
二、题目2：线性方程组求解
1.实验内容
2.算法原理
3.算法流程图
4.程序代码
5.执行结果及结果分析
6.体会
三、题目3：插值方法
1.实验内容
2.算法原理
3.算法流程图
4.程序代码
5.执行结果及结果分析
6.体会
四、题目4：最小二乘法曲线拟合
1.实验内容
2.算法原理
3.算法流程图
4.程序代码
5.执行结果及结果分析
6.体会
五、题目5：定积分的数值计算
1.实验内容
2.算法原理
3.算法流程图
4.程序代码
5.执行结果及结果分析
6.体会
六、题目6：常微分方程初值问题的数值解法
1.实验内容
2.算法原理
3.算法流程图
4.程序代码
5.执行结果及结果分析
6.体会
实
验
报
告
课程：
姓名：
班级：
学号：
老师：
数值计算实践
陈志博
信科 1602
1302160216
袁修贵
目录
一、题目 1：非线性方程求解 ................................................. 2
1.实验内容 ............................................................. 2
2.算法原理 ............................................................. 2
3.算法流程图 ........................................................... 3
4.程序代码 ............................................................. 4
5.执行结果及结果分析 ................................................... 7
6.体会 ................................................................. 7
二、题目 2：线性方程组求解 ................................................ 10
1.实验内容 ............................................................ 10
2.算法原理 ............................................................ 10
3.算法流程图 .......................................................... 12
4.程序代码 ............................................................ 14
5.执行结果及结果分析 .................................................. 18
6.体会 ................................................................ 20
三、题目 3：插值方法 ...................................................... 21
1.实验内容 ............................................................ 21
2.算法原理 ............................................................ 21
3.算法流程图 .......................................................... 22
4.程序代码 ............................................................ 22
5.执行结果及结果分析 .................................................. 24
6.体会 ................................................................ 26
四、题目 4：最小二乘法曲线拟合 ............................................ 27
1.实验内容 ............................................................ 27
2.算法原理 ............................................................ 27
3.算法流程图 .......................................................... 28
4.程序代码 ............................................................ 28
5.执行结果及结果分析 .................................................. 29
6.体会 ................................................................ 29
五、题目 5：定积分的数值计算 .............................................. 30
1.实验内容 ............................................................ 30
2.算法原理 ............................................................ 30
3.算法流程图 .......................................................... 31
4.程序代码 ............................................................ 31
5.执行结果及结果分析 .................................................. 33
6.体会 ................................................................ 34
六、题目 6：常微分方程初值问题的数值解法 .................................. 35
1.实验内容 ............................................................ 35
2.算法原理 ............................................................ 35
3.算法流程图 .......................................................... 37
4.程序代码 ............................................................ 39
5.执行结果及结果分析 .................................................. 41
6.体会 ................................................................ 42
1
一、题目 1：非线性方程求解
1.实验内容
采用两种常见的求解方法二分法和 Newton 法及改进的 Newton 法。
1. 用二分法计算方程
sin
在[1，2]内的根。(
610*5
,下同)
0
x
2
x
2
01
x
在[1，1.5]内的根。
3
x
2. 用二分法计算方程
3. 用 Newton 法求解下列方程
x0=0.5；
x0=1；
0
01 xxe
3
01
x
x
(
2()1
x
x
a)
b)
c)
2
x0=0.45, x0=0.65；
4. 用改进的 Newton 法求解，有 2 重根，取 2
)1
(
x
2
2()1
x
)1
0
x0=0.55；
要求：对给出的结果（收敛点，迭代次数）进行比较分析（讨论初始点选择、参
数选择对计算的影响）。
2.算法原理
对于一个非线性方程的数值解法很多。在此介绍两种最常见的方法：二分法
和 Newton 法。
对于二分法，其数学实质就是说对于给定的待求解的方程 f(x)，其在[a,b]上连
续，f(a)f(b)<0，且 f(x)在[a,b]内仅有一个实根 x*，取区间中点 c，若，则 c 恰为其
根，否则根据 f(a)f(c)<0 是否成立判断根在区间[a,c]和[c,b]中的哪一个，从而得出
新区间，仍称为[a,b]。重复运行计算，直至满足精度为止。这就是二分法的计算
思想。
Newton 法通常预先要给出一个猜测初值 x0，然后根据其迭代公式
x
1
k
x
k
(
xf
k
'
(
f
x
k
)
)
产生逼近解 x*的迭代数列{xk}，这就是 Newton 法的思想。当 x0 接近 x*时收敛很快，
但是当 x0 选择不好时，可能会发散，因此初值的选取很重要。另外，若将该迭代
公式改进为
x
1
k
x
k
(
xfr
k
'
(
x
f
k
)
)
其中 r 为要求的方程的根的重数，这就是改进的 Newton 法，当求解已知重数的方
程的根时，在同种条件下其收敛速度要比 Newton 法快的多。
2
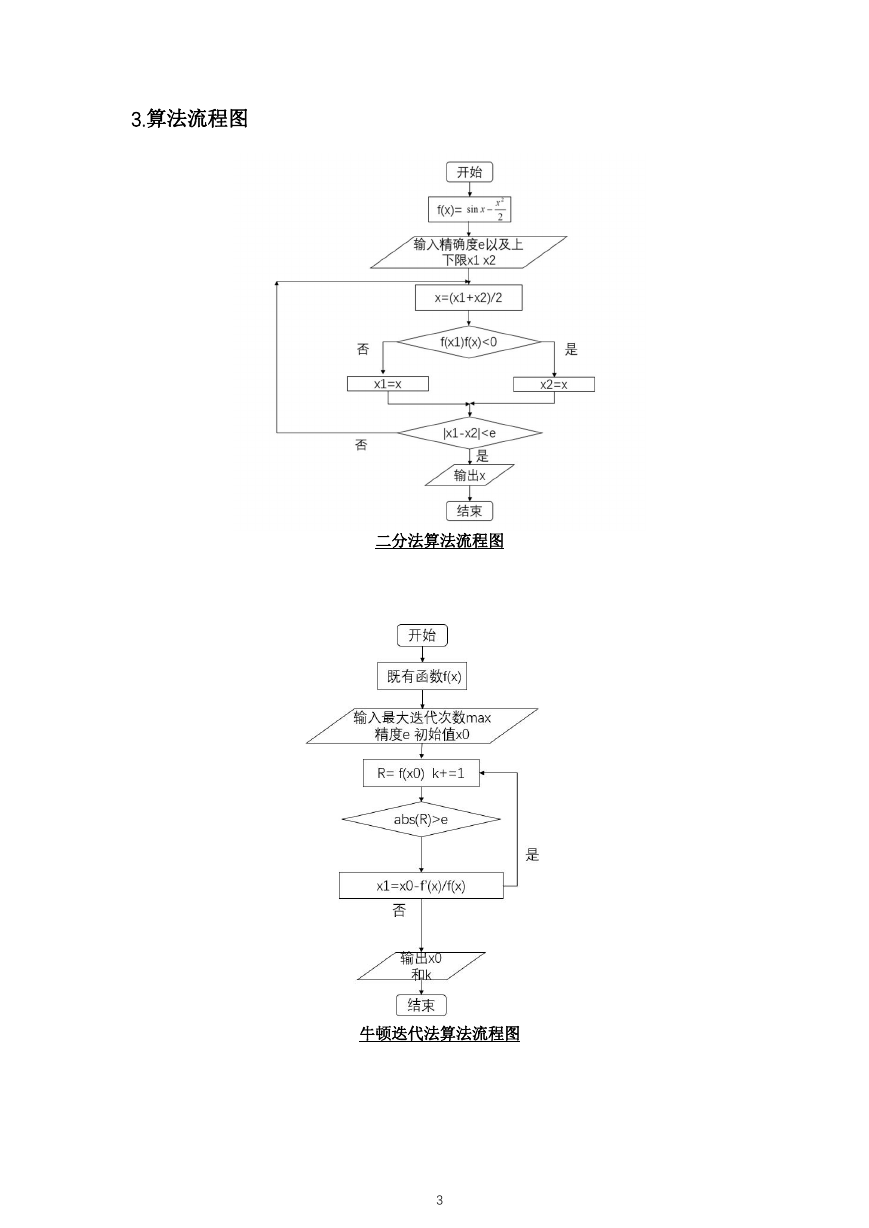
3.算法流程图
二分法算法流程图
牛顿迭代法算法流程图
3
改进的牛顿法算法流程图
4.程序代码
1. 二分法求 sin(x)-x^2/2 的根
%输出想要计算的函数
function y = ifunction(x)
y = sin(x)-x^2/2;
end
%二分法
function dichotomy()
x1=input('请输入求根区间的下限，x1=');
x2=input('请输入求根区间的上限，x2=');
e=input('请输入求根的精度，e=');
f1=ifunction(x1);
f2=ifunction(x2);
if f1*f2>0
disp('根不在区间中，请重新输入新的区间 ');
y=dichoyomyRoot(x1,x2,e);
disp('所求的根 root='),disp(y);
else
end
end
%二分法中的求根
function y=dichoyomyRoot(x1,x2,e)
x=(x1+x2)/2;
4
f3=ifunction(x);
f1=ifunction(x1) ;
if(f1*f3<0)
r=x-x1;
if(r>e)
x2=x;
y=dichoyomyRoot(x1,x2,e);
else
end
y=x;
r=x2-x;
if(r>e)
else
x1=x;
y=dichoyomyRoot(x1,x2,e);
else
end
y=x ;
end
end
2. 二分法求 x^3-x-1 的根
同上
修改 function ifunction 中的函数即可
function y = ifunction(x)
y = x^3-x-1;
end
3.a 牛顿法求 x*exp(x)-1 的根
%输出想要计算的函数
function y = ifunction(x)
y = x*exp(x)-1;
end
%牛顿法
syms x;
f=ifunction(x);
df=diff(f);
x0=input('请输入初始值 x0=');
k=0;
max=100; %迭代最大次数
e=5e-6; %精度
R=eval(subs(f,'x','x0'));
while (abs(R)>e)
x1=x0-eval(subs(f,'x','x0'))/eval(subs(df,'x','x0'));
R=x1-x0;
x0=x1;
k=k+1;
5
if k>max
disp('迭代不收敛');
end
end
k
x = x0 %所求得的近似解
%迭代次数
3.b 牛顿法求 x^3-x-1 的根
同上 3.a
修改 function ifunction 中的函数即可
function y = ifunction(x)
y = x^3-x-1;
end
3.c 牛顿法求(x-1)^2*(2*x-1)的根
同上 3.a
修改 function ifunction 中的函数即可
function y = ifunction(x)
y = (x-1)^2*(2*x-1);
end
4.改进牛顿法求(x-1)^2*(2*x-1)的根
%输出想要计算的函数
function y = ifunction(x)
y = (x-1)^2*(2*x-1);
end
%牛顿法
syms x;
f=ifunction(x);
df=diff(f);
x0=input('请输入初始值 x0=');
k=0;
max=100; %迭代最大次数
e=5e-6; %精度
R=eval(subs(f,'x','x0'));
r=2; %改进的牛顿法：r 为要求的方程的根的重数
while (abs(R)>e)
x1=x0-r*eval(subs(f,'x','x0'))/eval(subs(df,'x','x0'));
R=x1-x0;
x0=x1;
k=k+1;
if k>max
disp('迭代不收敛'); break;
end
end
k
x = x0 %所求得的近似解
%迭代次数
6
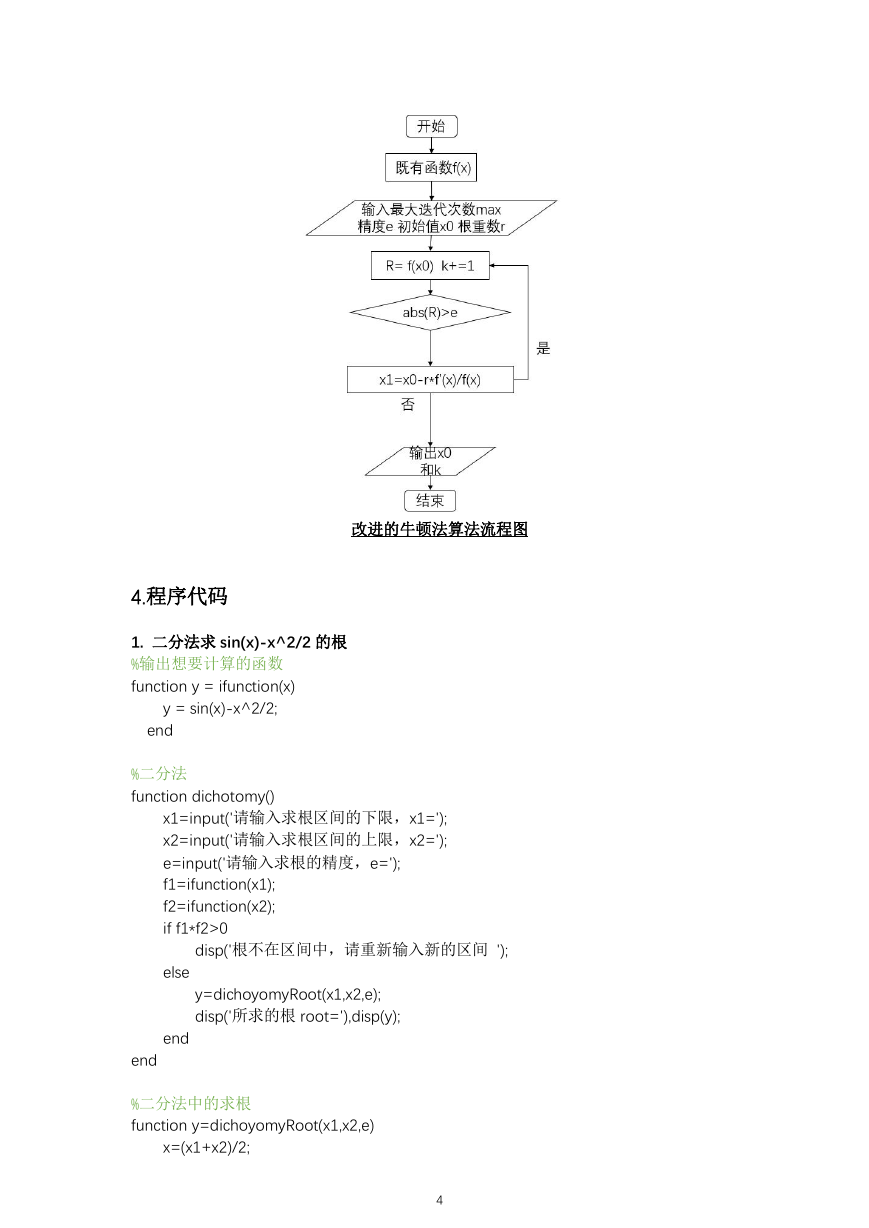
5.执行结果及结果分析
1. 二分法求 sin(x)-x^2/2 的根
将结果代入原函数发现满足精度要求，但是迭代次数较多，收敛的速度较慢
2. 二分法求 x^3-x-1 的根
同上题，将结果代入原函数发现满足精度要求，但是迭代次数较多，收敛的速度较慢
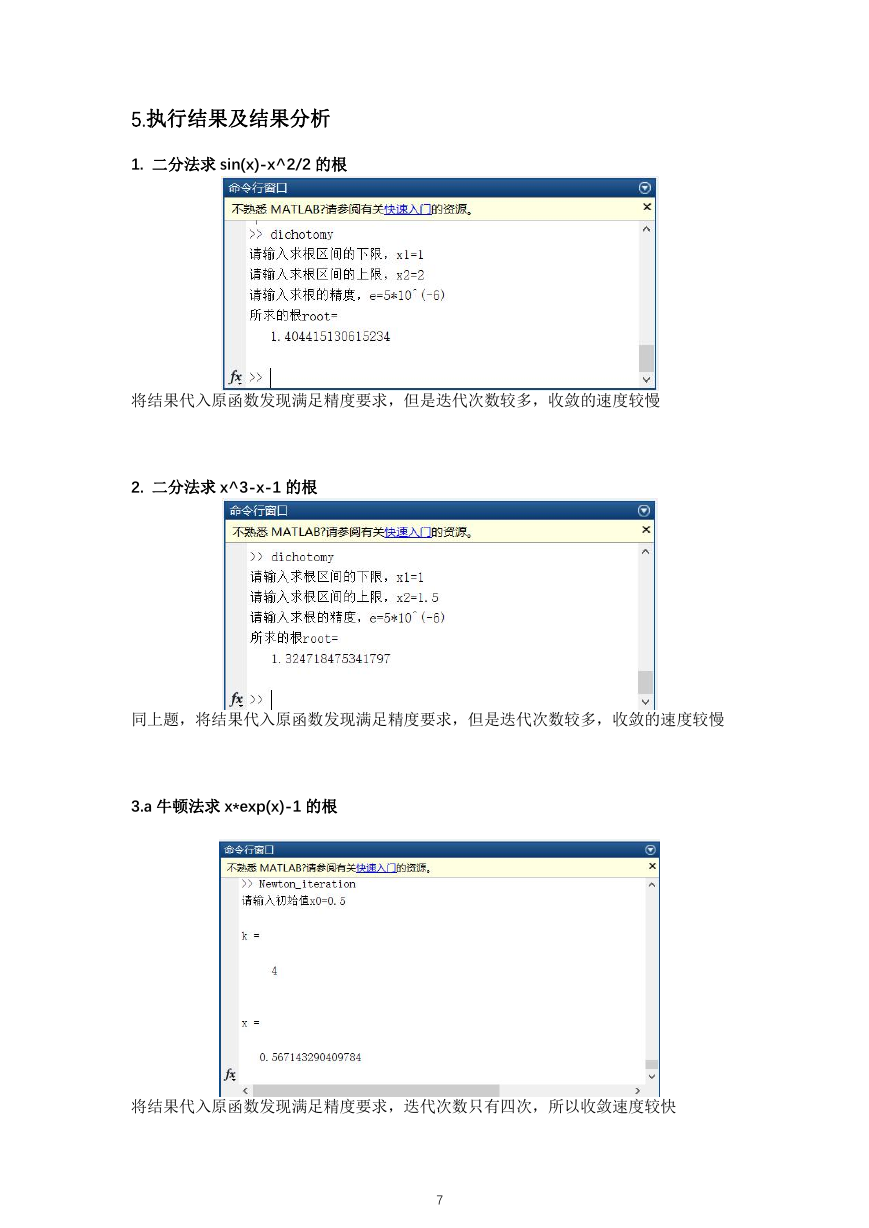
3.a 牛顿法求 x*exp(x)-1 的根
将结果代入原函数发现满足精度要求，迭代次数只有四次，所以收敛速度较快
7
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
