logo资料库

联邦滤波各种结构性能与容错性分析.docx

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：0.90M 资料格式：docx 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    联邦滤波
    一、信息分配原则和全局最优估计
    二、联邦滤波器的设计步骤
    三、联邦滤波器的6种结构与性能分析
    四、6类联邦滤波器的容错性能
    五、残差检验法
    六、子、主滤波器的滤波方程
    联邦滤波 目录 联邦滤波......................................................................................1 一、信息分配原则和全局最优估计...................................2 二、联邦滤波器的设计步骤............................................... 2 三、联邦滤波器的 6 种结构与性能分析...........................2 四、6 类联邦滤波器的容错性能........................................7 五、残差 2 检验法.............................................................. 7 六、子、主滤波器的滤波方程...........................................8 1
    一、信息分配原则和全局最优估计 联邦滤波器是一种两级滤波机构，公共参考子系统惯导的输出 kX 一方面给 主滤波器，另一方面给各子滤波器作为量测值。各子系统的输出只给各自的滤波 器。各子滤波器的局部估计值 iX 及其协方差阵 iP 送入主滤波器和主滤波器的 估计值一起进行融合得到全局估计值。  由主滤波器和子滤波器合成的全局最优估计值 gX 及其相应的协方差阵 gP  被放大为 1 gP 后再反馈给子滤波器，来重置子滤波器的估计值，即： i  X = X ,P ii 不同的 i可以得到不同结构的联邦滤波器。 。主滤波器的协方差阵为 1 1  P i g m gP ， i 根据信息分配原则确定， g i 二、联邦滤波器的设计步骤 （1）将子滤波器和主滤波器的初始估计协方差阵设置为组合系统初始值的 i 倍， 其中  =  1 ， N i=1   m  i  1 。 （2）将子滤波器和主滤波器的过程噪声协方差阵设置为组合系统过程噪声协方 差阵的 i 倍。 （步骤（1）和（2）多采用方差上界技术使各子滤波器初始滤波器估计协方差阵 和过程噪声协方差阵互不相关） （3）各子滤波器处理自己的量测信息，获得局部估计。 （4）在得到各子滤波器的局部估计和主滤波器的估计后按照公式进行最优合成。 公式如下：  X g  P g   P X ii 1 i N  i 1  P g N  =   1  i 1  P ii  1    （5）用全局滤波来重置各子滤波器和主滤波器的滤波器值和协方差阵。 三、联邦滤波器的 6 种结构与性能分析 设计联邦滤波器时，不同的信息分配系数会使联邦滤波器有不同的结构和特  性，如：容错性、最优性、计算性等，根据 i 不同，可以把联邦滤波器的设计机构分为下面 6 种： 1、第 1 类结构（  “零化式”重置结构 ）   i 1 = / 1 , 0 | , m     i 1 , i ,N ,m  的分配原则 2
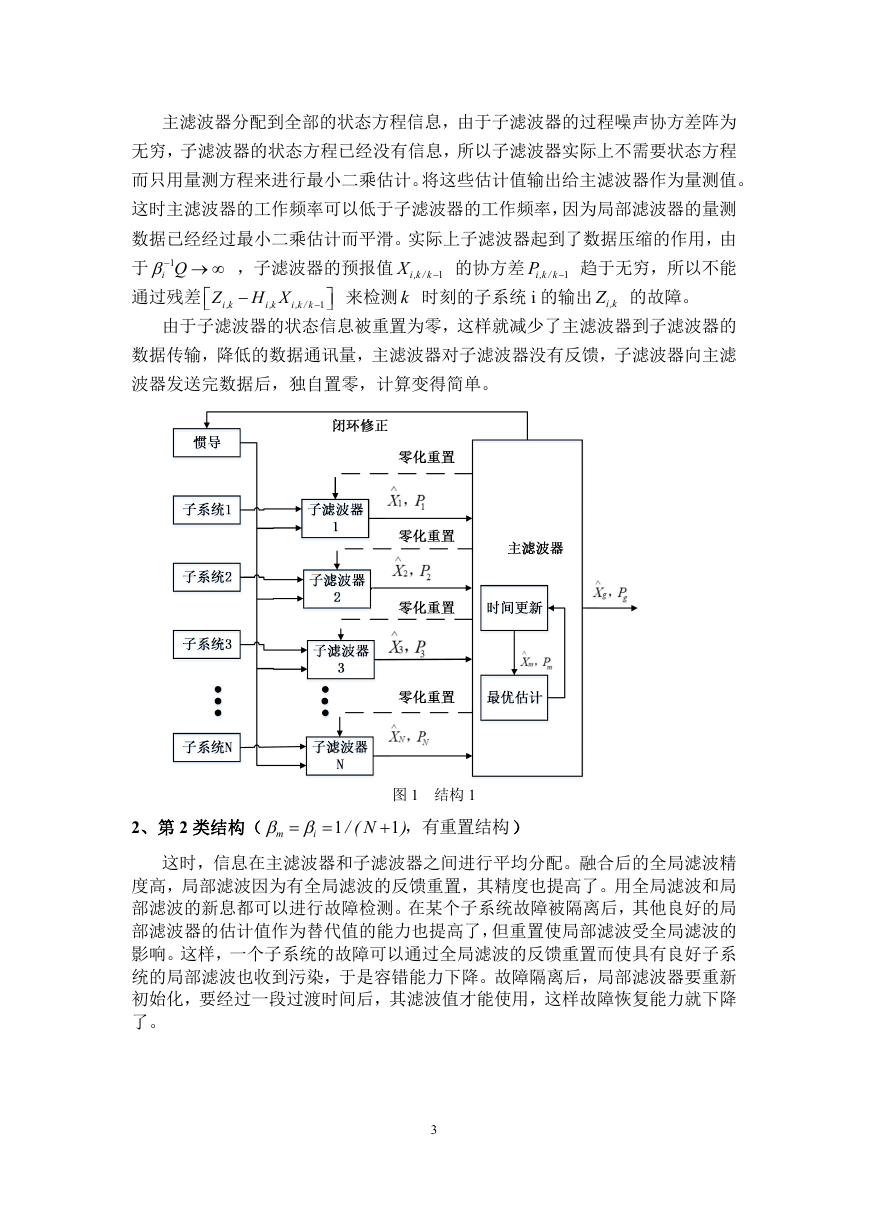
    主滤波器分配到全部的状态方程信息，由于子滤波器的过程噪声协方差阵为 无穷，子滤波器的状态方程已经没有信息，所以子滤波器实际上不需要状态方程 而只用量测方程来进行最小二乘估计。将这些估计值输出给主滤波器作为量测值。 这时主滤波器的工作频率可以低于子滤波器的工作频率，因为局部滤波器的量测 数据已经经过最小二乘估计而平滑。实际上子滤波器起到了数据压缩的作用，由 i,k / kP  趋于无穷，所以不能 于 1 i Q   ，子滤波器的预报值 1 i,k / kX  的协方差 1 通过残差 Z   i,k  H X i,k i,k / k 1   来检测 k 时刻的子系统 i 的输出 i,kZ 的故障。  由于子滤波器的状态信息被重置为零，这样就减少了主滤波器到子滤波器的 数据传输，降低的数据通讯量，主滤波器对子滤波器没有反馈，子滤波器向主滤 波器发送完数据后，独自置零，计算变得简单。 2、第 2 类结构（   i m  1 / ( N 图 1 结构 1 1 )  ，有重置结构 ） 这时，信息在主滤波器和子滤波器之间进行平均分配。融合后的全局滤波精 度高，局部滤波因为有全局滤波的反馈重置，其精度也提高了。用全局滤波和局 部滤波的新息都可以进行故障检测。在某个子系统故障被隔离后，其他良好的局 部滤波器的估计值作为替代值的能力也提高了，但重置使局部滤波受全局滤波的 影响。这样，一个子系统的故障可以通过全局滤波的反馈重置而使具有良好子系 统的局部滤波也收到污染，于是容错能力下降。故障隔离后，局部滤波器要重新 初始化，要经过一段过渡时间后，其滤波值才能使用，这样故障恢复能力就下降 了。 3
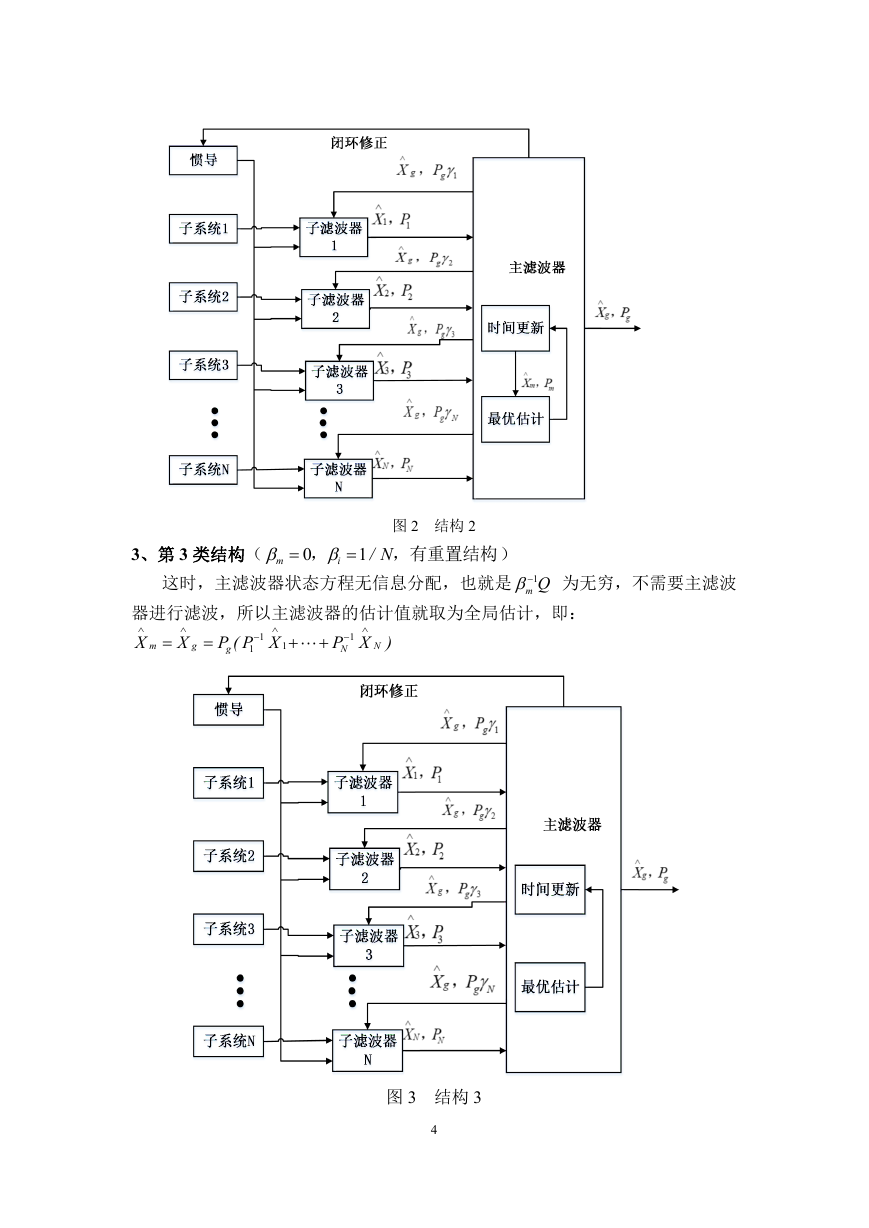
    3、第 3 类结构（  m  i 0 ， 1 图 2 结构 2 ，有重置结构 ） / N 这时，主滤波器状态方程无信息分配，也就是 1 m Q 为无穷，不需要主滤波 器进行滤波，所以主滤波器的估计值就取为全局估计，即：  X  P ( P X g   X 1  P X ) N N 1  1  1  g  m  图 3 结构 3 4
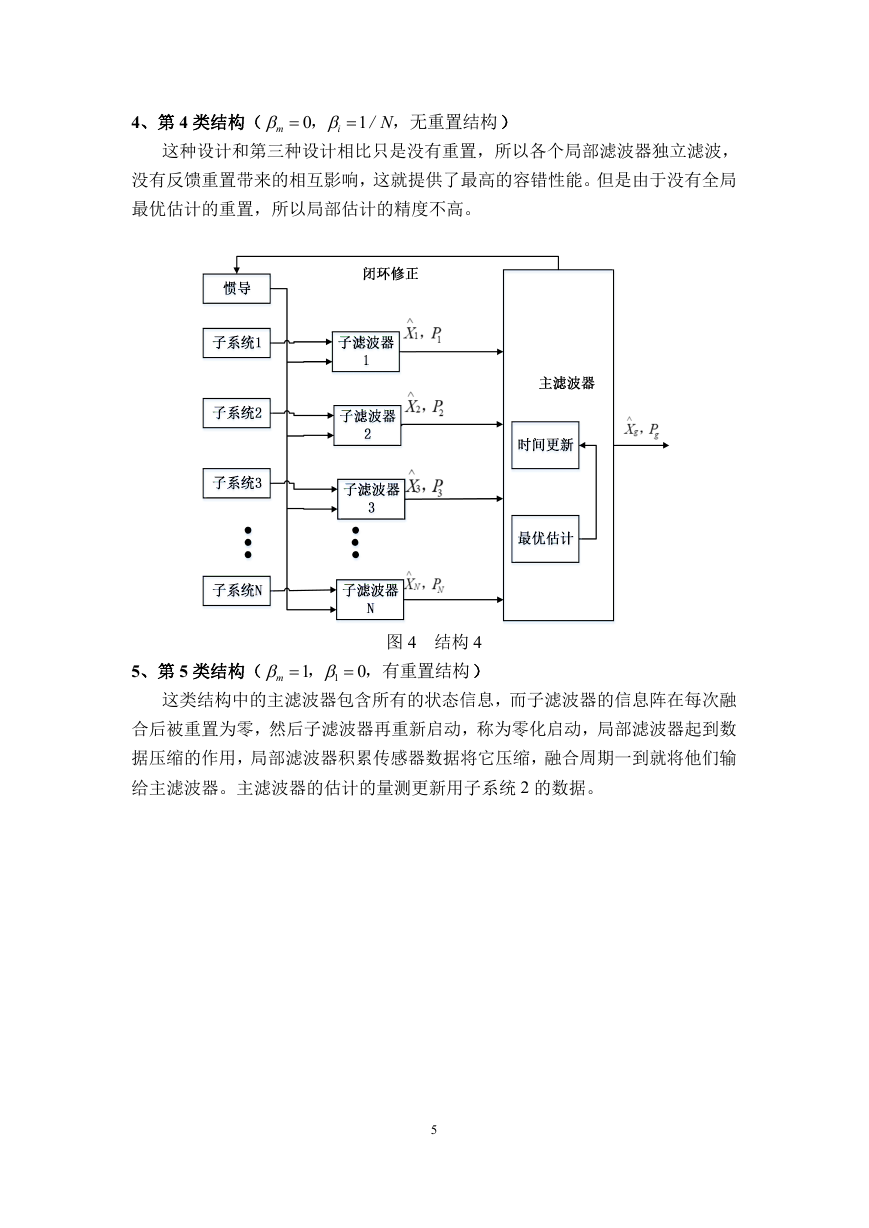
    4、第 4 类结构（  m  i 0 ， 1 / N ，无重置结构 ） 这种设计和第三种设计相比只是没有重置，所以各个局部滤波器独立滤波， 没有反馈重置带来的相互影响，这就提供了最高的容错性能。但是由于没有全局 最优估计的重置，所以局部估计的精度不高。 5、第 5 类结构（ m 1  ， 1 图 4 结构 4 0 ，有重置结构） 这类结构中的主滤波器包含所有的状态信息，而子滤波器的信息阵在每次融 合后被重置为零，然后子滤波器再重新启动，称为零化启动，局部滤波器起到数 据压缩的作用，局部滤波器积累传感器数据将它压缩，融合周期一到就将他们输 给主滤波器。主滤波器的估计的量测更新用子系统 2 的数据。 5
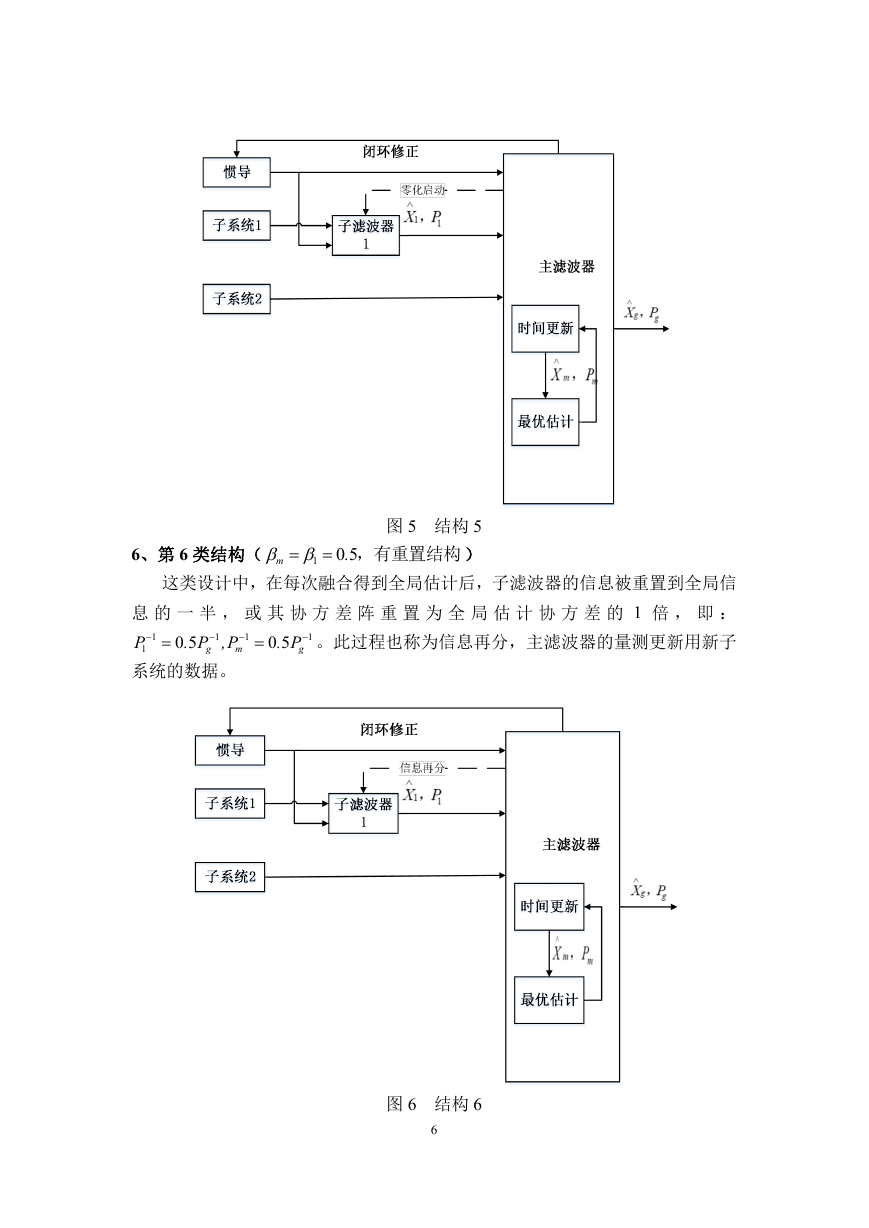
    6、第 6 类结构（   1 m 图 5 结构 5  ，有重置结构 ） 0 5 . 这类设计中，在每次融合得到全局估计后，子滤波器的信息被重置到全局信 息 的 一 半 ， 或 其 协 方 差 阵 重 置 为 全 局 估 计 协 方 差 的 1 倍 ， 即 ： 0 5   P . P ,P 。此过程也称为信息再分，主滤波器的量测更新用新子 1 m 系统的数据。 0 5  . P g  1  g 1 1  1 图 6 结构 6 6
    四、6 类联邦滤波器的容错性能 1、第 1 类结构（   i 1 , m  “零化式”重置结构 ） 0 , | 这种结构的子滤波器的故障检测和隔离能力很差。因为子滤波器的状态信息 分配为零，协方差趋于无穷。而主滤波器拥有未发生故障前的全部信息，因此 FDI 能力强。这种结构的 FR 能力中等，在有故障子系统的数据被主滤波器使用 后，全局解将受到污染。虽然这时其他子系统的滤波器未被污染，但他们却只起 最小二乘估计作用，他们的解不具有长记忆的特性，不能外推使用。因此不能用 他们来使主滤波器迅速进行故障恢复。主滤波器在故障子系统隔离后必须重新初 始化，经过一段过渡时间才能从故障中恢复。 2、第 2 类结构（ 1  ，有重置结构 ） / ( N   i 1  ) m 这种结构的子滤波器的 FDI 能力较好。主滤波器的 FDI 能力中等。在一个子 系统发生故障后，主滤波器将受到它的污染，再通过重置使其他子滤波器污染， 故在故障子系统被隔离后，主子滤波器都要初始化，FR 能力与第 1 种结构相同。 3、第 3 类结构（ ，有重置结构 ） 0 ， / N  i  m 1 容错性能基本上和第 2 种一样。但 m  ，主滤波器的 FDI 能力差。 0 4、第 4 类结构（  m  i 0 ， 1 / N ，无重置结构 ） 由于无重置，各子滤波器不会互相影响，因此这种结构的容错性能最好。 5、第 5 类结构（ m 1  ， 1 0 ，有重置结构） 子滤波器的 FDI 能力差。主滤波器的 FDI 能力强，但 FR 能力差（因为需要 重新初始化） 6、第 6 类结构（   1 m  ，有重置结构 ） 0 5 . 主、子滤波器的 FDI 能力中等。同样主滤波器的 FR 能力差。 总之，如不将融合后的全局状态估计和协方差阵去反馈重置子滤波器，那么 就不会产生子滤波器的交叉感染，子滤波器的精度虽然下降，但联邦滤波器的容 错能力却大大提高了。 五、残差 2 检验法 用残差 2 检验对系统的故障进行检测和隔离。由于每个局部滤波器均为卡 尔曼滤波器，其残差为： 其中预报值  X k / k 1    k / k 1  r k  X 是零均值的白噪声，其方差为：  1 k - k 1  k / k  Z H X  k 。当无故障发生时卡尔曼滤波器的残差 kr  。当系统发生故障时，  A H P H k R k k / k T k 1  k 7
    残差的均值就不再为零了。因此对残差的检验可以确定系统是否发生了故障。 对 kr 做二元假设： 0 无故障时：   E r k  有故障时：   E r k    T ,E r r k k   ,E r k    ； A k  r  k T     A k 可推出故障检测函数为：  k  式中 k 时服从自由度为 m 的 2 分布，即 故障判定准则为： 1 r A r k k  k 2   k ( m ) 。m 为量测 kZ 的维数。    若 若  k  k   T , D T , D 判定有故障 判定无故障 其中设置的门限值 DT 可由误警率 fP 确定。 误检率 fP  可由下面积计算公式求出：        ,n d 1   P f  2 T D T D 0 2     ,n d  给定 fP  ，就可以由 2 分布求出 DT 。 2 分布的部分内容如下表所示： n  110 210 310 410 510 610 710 810 910 1 2.71 6.63 10.83 15.14 19.51 23.93 28.37 32.84 37.32 2 4.61 9.21 13.82 18.42 23.03 27.63 32.24 36.84 41.45 3 6.25 11.34 16.27 21.11 25.9 30.66 35.41 40.13 44.84 六、子、主滤波器的滤波方程 系统信息在主、子滤波器间的分配方法是基于信息分配原则的，即满足： 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料