PCA: Primary Component Analysis November 27, 2015 1 PCA理理理论论论推推推导导导 X =  x1,1 x1,2 x2,2 x2,1 ... ... xm,1 xm,2 ... x1,n ... x2,n ... ... ... xm,n  (1) X ∈ Rm×n， 式(1)的 每 列 是 一个 样 本 ， 每 个 样 本有m个 属 性 ， 一 共 有n个样本。注意，这里的每个样本都经过均值化处理。 X表示一个完整数据集。举例来说，一台设备上有m个测点，这些测点 定义了设备的运行特征，采集数据n秒，就形成X。 数据通常是含糊的，有噪声的，不明确的。这种含糊和不明确，体现在 它的协方差阵的多数元素都是非零值。比如，X的协方差阵就是: CX = 1 n − 1 XX T 是一个实数系数，CX ∈ Rm×m。 (2) 其中， 1 n−1 需要从数据找到一个不含糊的，低噪声的方向。这个需求，在本质上就 是寻找一个矩阵，用它对X做变换，使得变换后的新矩阵的协方差阵大多 数元素的值是零，最好的情况是，只有主对角线非零，其他都是零。令P 表 示这个矩阵，则： 其中，P ∈ Rm×m,Y ∈ Rm×n。 把式(3)带入式(2)，令 Y = P X A = XX T 则： CY = = = = 1 1 n − 1 n − 1 n − 1 n − 1 1 1 Y Y T (P X)(P X)T P XX T P T P AP T 1 (3) (4) (5) 

A是一个对称阵，对它进行对角化，可以写成A = EDET ，其中，D是 对角阵，{A, E, D} ∈ Rm×m。 对角化性质可知，P −1 = P T ，I表示单位阵，则式(5)就变成： 如果要将CY 转化成对角阵，观察上式可知，如果令P = ET ，根据矩阵 CY = = = = = = 2 均均均值值值化化化 1 1 1 1 1 n − 1 n − 1 n − 1 n − 1 n − 1 n − 1 1 P AP T P (P T DP )P T (P P T )D(P P T ) (P P −1)D(P P −1) IDI D PCA理论推导里的X经过均值化处理的。均值化过程如下：  z1,1 z2,1 ... zm,1 Z =  z1,2 z2,2 ... zm,2 z1,n ... z2,n ... ... ... ... zm,n 其中，Z ∈ Rm×n，是原始数据。 令: zi = 1 n n j=1 zi,j 那么，均值化就是：  z1,1 − z1 ... z1,2 − z1 z2,2 − z2 z1,n − z1 z2,n − z2 z2,1 − z2 zm,1 − zm zm,2 − zm ... zm,n − zm ... ... ... ... ... Z = 3 实实实现现现 用Python2.7，matplotlib和numpy实现pca算法。 2 (6) (7) (8) (9)  

# !/ usr / bin / env python # ! -* - coding : utf - 8 -* - import m a t p l o t l i b . pyplot as plt from numpy import * # create two data set def c r e a t e _ d a t a s e t ( n ) : data_r = random . randn (n , 2 ) # squeez y for i in range ( data_r . shape [ 0 ] ) : data_r [i , 1 ] = 0 . 1 * data_r [i , 1 ] # rotate theta = - 0 . 25 * 3 . 14 tran = zeros (( 2 , 2 ) ) tran [1 , 1 ] = tran [0 , 0 ] = cos ( theta ) tran [0 , 1 ] = - sin ( theta ) tran [1 , 0 ] = sin ( theta ) data = dot ( data_r , tran ) # move data [ : , 0 ] + = 3 data [ : , 1 ] + = 1 return data . t r a n s p o s e () def do_mean ( X ) : zeros (( X . shape [ 0 ] ,1 ) ) means = means [0 , 0 ] = mean ( X [0 , : ] ) means [1 , 0 ] = mean ( X [1 , : ] ) for i in range ( X . shape [ 0 ] ) : X [i , : ] - = means [i , 0 ] return X def do_pca ( X ) : A = dot (X , X . t r a n s p o s e () ) _ , E = linalg . eig ( A ) P = E . t r a n s p o s e () return dot (P , X ) def draw_x ( X ) : plt . axis ( [ -3 , 6 , -6 , 6 ] ) plt . plot ( [ z for z in X [0 , : ] ] , [ z for z in X [1 , : ] ] , ’r . ’) plt . show () def main () : X = c r e a t e _ d a t a s e t ( 1000 ) draw_x ( X ) do_mean ( X ) new_X = do_pca ( X ) draw_x ( new_X ) if _ _na me_ _ = = " _ _ma in_ _ " : main () 3 

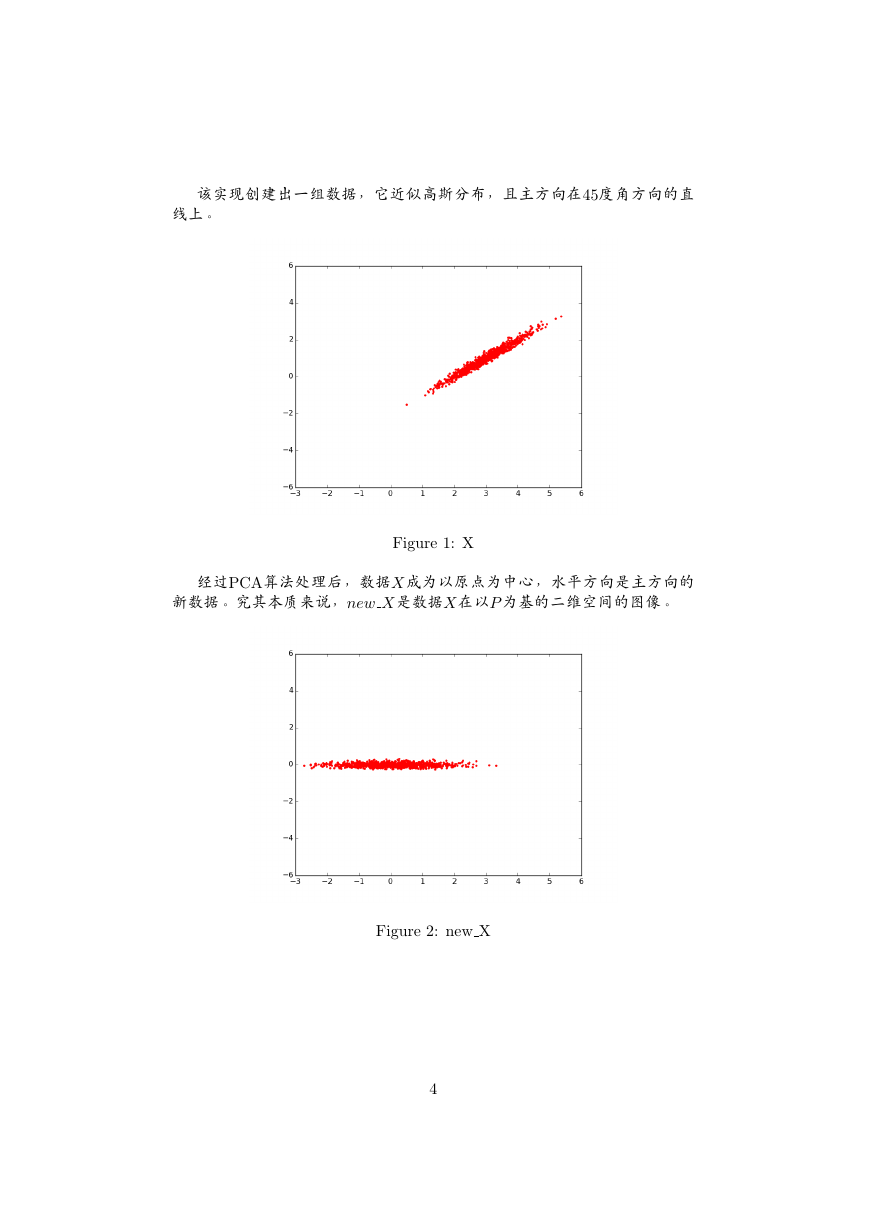
该实现创建出一组数据，它近似高斯分布，且主方向在45度角方向的直 线上。 Figure 1: X 经过PCA算法处理后，数据X成为以原点为中心，水平方向是主方向的 新数据。究其本质来说，new X是数据X在以P 为基的二维空间的图像。 Figure 2: new X 4