第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
2016年广东实验中学附属天河学校小升初数学真题及答案C卷.doc
2016 年广东实验中学附属天河学校小升初数学真题及答案 C 卷
（满分：120 分 时间：80 分钟）
第一卷(70 分)
一、填空题(每小题 2 分，第 2~3 题每空 1 分，共 20 分)
1、一条绳长 6 米，剪了 5，还剩
2.在下面的横线上填“>”“<”或“=”。
米。
3.5
2.8，
千克=
克，
3.
3
8
100 千克
吨，
2 23
7
1
3
3
20
2
7
，
2 9
3 7
1
20
9
7
，
千米=
4 3
5 4
米，
3
5
4
5
升=
毫升，
时=
分，
分米
米（用分数表示）
4.在括号里填上合适的数:0.75=
÷16=
％。
5.把长
6
11
米的钢管平均分成 3 段，每段占全长的
，每段长
米。
6.0.3:0.75 化成最简整数比是
，比值是
。
7.计划行一段路，已行了全路的
5
8
。已行的和未行的路程的比是
。
二、判断题(正确的打“√”，错误的打“×”，共 5 分
1.一次植树的成活率是 90%，表示有 10 棵树没成活。
2.一个大于 0 的数除以
1
8
，等于把这个数扩大 8 倍。
3.在平面图中 A(6，4)和 B(4，6)，表示的是同一点。
4.一个比的前项和后项同时乘或除以相同的数，比值不变。
5.一台电脑的价格是 5000 元，先降价 10%，再涨价 10%，价格不变。
三、选择题(每小题 2 分，共 10 分)
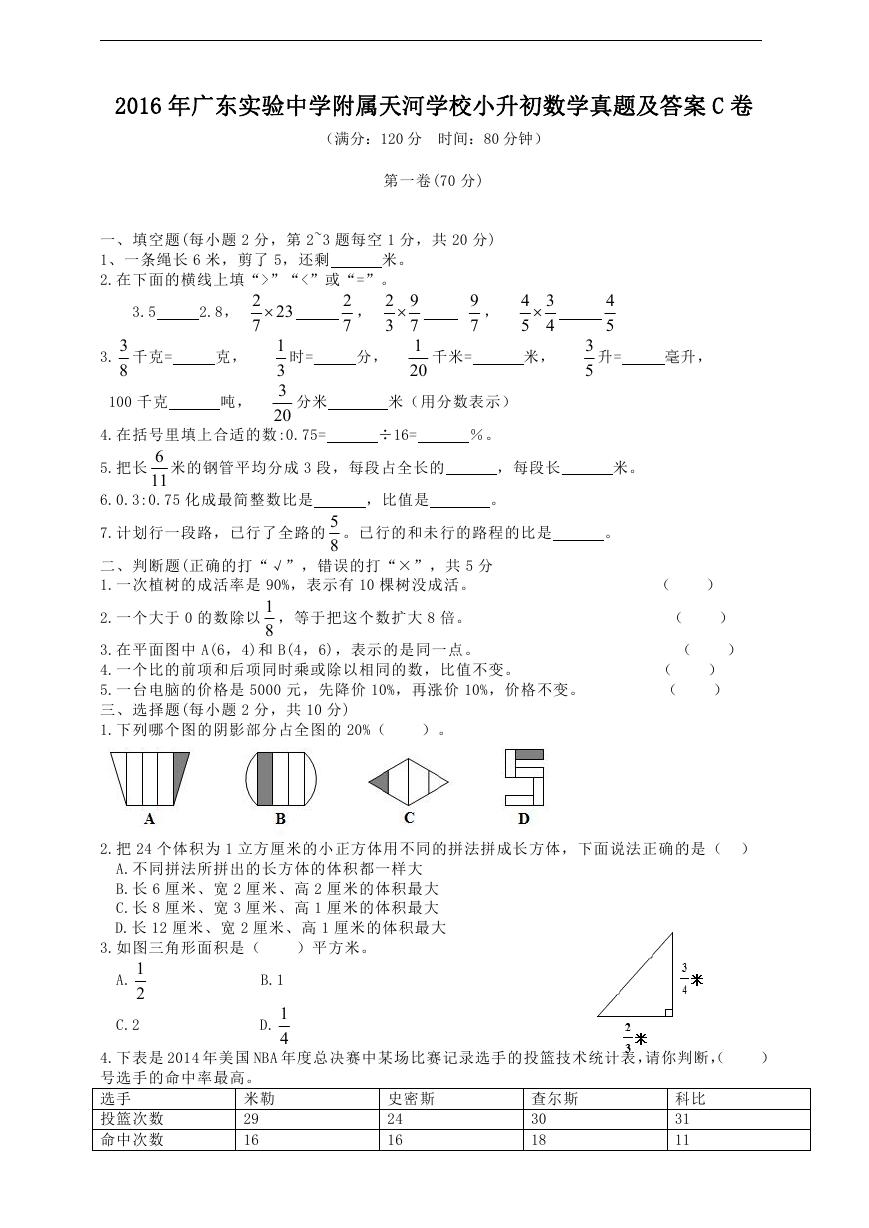
1.下列哪个图的阴影部分占全图的 20%（
）。
（
）
（
）
（
）
（
（
）
）
2.把 24 个体积为 1 立方厘米的小正方体用不同的拼法拼成长方体，下面说法正确的是（ ）
A.不同拼法所拼出的长方体的体积都一样大
B.长 6 厘米、宽 2 厘米、高 2 厘米的体积最大
C.长 8 厘米、宽 3 厘米、高 1 厘米的体积最大
D.长 12 厘米、宽 2 厘米、高 1 厘米的体积最大
3.如图三角形面积是（
）平方米。
A.
1
2
C.2
B.1
D.
1
4
4.下表是 2014 年美国 NBA 年度总决赛中某场比赛记录选手的投篮技术统计表，请你判断，（
号选手的命中率最高。
选手
投篮次数
命中次数
史密斯
24
16
查尔斯
30
18
米勒
29
16
科比
31
11
）
A.米勒
B.史密斯
C.查尔斯
D.科比
5.一顶工程，甲队单独做 5 天完成，乙队单独做 7 天完成，甲、乙两队每天完成的工作量的比
是（
）
A.5:7
B.7:5
C.1:12
D.1:35
四、计算题(共 20 分)
1.直接写出得数。(每小题 1 分，共 4 分)
5
12
36
3 8
2 5
5.1
4
17
7
8
4 21
2.下面各题，怎样算简便就怎样算。(每小题 3 分，共 12 分)
1 4
6 5
3
7
（2）
42
5
6
（1）
5
6
（3）
9
3
5
9
5
（4） 68.4 4 68.4 3 68.4 3
3.求未知数 x 。(每小题 2 分，共 4 分)
（1）
3
4
x
12
17
（2）
x
2
9
5
1
6 18
五、解决问题(每小题 5 分，共 15 分)一
1.要捆扎一种礼盒(如图)。打结处的绳长 30 厘米，这根包装绳总长是多少厘米?
2.广州白云山风景区 2014 年一共接待 392 万游客，其中上半年接待的游客数占全年的
季度接待的游客数是上半年的
3
4
，第三季度接待游客多少万人?
3
7
，第三
3.一个正方体的玻璃容器棱长是 10 厘米，先给这个容器注入 4 厘米的水，再把 2 个一样的钢球
放进里面，容器的水上升了 3 厘米，一个钢球的体积是多少立方厘米?
一、解决问题（共 30 分）
1.(3 分)“哥德巴赫猜想”是说：每个大于 2 的偶数都可以表示成两个两位质数的和，问:168
是哪两个两位质数的和，并且其中一个质数的个位是 1?
第二卷（50 分）
2.(17 分)下面是小明家十一月份支出及储蓄情况统计图。
(1)(3 分)小明家十一月份的伙食共花了 1200 元，小明家的储蓄是多少元
(2)(10 分)根据扇形统计图，把下表填完整
项目
费用/元
百分比/%
伙食费
1200
40%
购物
水电费
储蓄
其他支出
总计
(3)(2 分)伙食费比购物多（
(4)(2 分)水电费比购物少（
）％
）％
3.(5 分)小明已经进行了 20 场比赛，并且胜率为 95%。若以后一场都不输，他还需要赢几场比
赛，才能使胜率达到 96%?
4.(5 分)一辆汽车从甲地向乙地行驶，行了一段距离后，距离乙地还有 210 千米，接着又行了全
程距离的 20%，此时已行驶的距离与未行驶的距离比为 3:2，求甲、乙两地的距离
二、附加题(20 分)
1.(4 分)图中大小正方形的边长分别是 9 厘米和 5 厘米，求阴影部分的面积。
2.(3 分)小玲和小华姐弟俩正要从公园门口沿马路向东去某地，而他们的家要从公园门口沿马路
往西。小华问姐姐:“是先向西回家取了自行车，再骑车向东去，还是直接从公园门口步行向东
去快”?姐姐算了一下说:“如果骑车与步行的速度比是 4:1，那么从公园门口到目的地的距离超
过 2 千米时，回家取车才合算。”请推算一下，从公园到他们家的距离是多少米?
3.(13 分)某中学计划建设一个 400，米跑道的运动场(如图所示)，聘请你任工程师，问：
(1)若直道长 100 米，则弯道弧长半径 r 为多少米？
(2)共 8 个跑道，每条宽 1.2 米，操场最外圈长多少米?
(3)若操场中心铺绿草，跑道铺塑胶，则各需绿草、塑胶多少平
方米？
(4)若绿草 50 元/平方米，塑胶 350 元平方米，学校现有 200 万
元?可以开工吗，为什么?
参考答案
（满分：120 分 时间：80 分钟）
第一卷(70 分)
一、填空题(每小题 2 分，第 2~3 题每空 1 分，共 20 分)
1、一条绳长 6 米，剪了 5，还剩 3.6 米。
2.在下面的横线上填“>”“<”或“=”。
3.5 ＝ 2.8，
3.
3
8
千克=
2 23
7
1
3
＞
时=
2
7
，
2 9
3 7
1
20
＜
千米=
9
7
，
＜
4
5
升=
600 毫升，
4 3
5 4
3
5
375 克，
20 分，
50 米，
100 千克 0.1 吨，
米（用分数表示）
3
20
分米
3
200
4.在括号里填上合适的数:0.75=
12 ÷16=
75 ％。
5.把长
6
11
米的钢管平均分成 3 段，每段占全长的
1
3
，每段长
2
11
米。
6.0.3:0.75 化成最简整数比是 2:5 ，比值是 0.4 。
7.计划行一段路，已行了全路的
5
8
。已行的和未行的路程的比是 5:3 。
二、判断题(正确的打“√”，错误的打“×”，共 5 分
1.一次植树的成活率是 90%，表示有 10 棵树没成活。
2.一个大于 0 的数除以
1
8
，等于把这个数扩大 8 倍。
3.在平面图中 A(6，4)和 B(4，6)，表示的是同一点。
4.一个比的前项和后项同时乘或除以相同的数，比值不变。
5.一台电脑的价格是 5000 元，先降价 10%，再涨价 10%，价格不变。
三、选择题(每小题 2 分，共 10 分)
1.下列哪个图的阴影部分占全图的 20%（ D ）。
（ × ）
（ √ ）
（ × ）
（ × ）
（ × ）
2.把 24 个体积为 1 立方厘米的小正方体用不同的拼法拼成长方体，下面说法正确的是（ A ）
A.不同拼法所拼出的长方体的体积都一样大
B.长 6 厘米、宽 2 厘米、高 2 厘米的体积最大
C.长 8 厘米、宽 3 厘米、高 1 厘米的体积最大
D.长 12 厘米、宽 2 厘米、高 1 厘米的体积最大
3.如图三角形面积是（ D ）平方米。
A.
1
2
C.2
B.1
D.
1
4
4.下表是 2014 年美国 NBA 年度总决赛中某场比赛记录选手的投篮技术统计表，请你判断，（ B ）
号选手的命中率最高。
选手
投篮次数
命中次数
A.米勒
史密斯
24
16
C.查尔斯
查尔斯
30
18
米勒
29
16
科比
31
11
B.史密斯
D.科比
5.一顶工程，甲队单独做 5 天完成，乙队单独做 7 天完成，甲、乙两队每天完成的工作量的比
是（ B ）
A.5:7
B.7:5
C.1:12
D.1:35
四、计算题(共 20 分)
1.直接写出得数。(每小题 1 分，共 4 分)
5
12
36
15
3 8
2 5
12
5
5.1
4
17
1.2
7
8
4 21
2
3
5
6
（1）
3
7
2.下面各题，怎样算简便就怎样算。(每小题 3 分，共 12 分)
1 4
6 5
29
30
【答案】17
【答案】
（2）
42
5
6
（3）
9
【答案】
3
5
14
3
9
5
（4） 68.4 4 68.4 3 68.4 3
【答案】684
3.求未知数 x 。(每小题 2 分，共 4 分)
（1）
【答案】
3
4
12
17
x
16
17
（2）
x
2
9
1
5
6 18
【答案】
5
486
五、解决问题(每小题 5 分，共 15 分)一
1.要捆扎一种礼盒(如图)。打结处的绳长 30 厘米，这根包装绳总长是多少厘米?
【解析】10×2+8×2+6×4+30=90(厘米)
答:这根包装绳总长是 90 厘米。
2.广州白云山风景区 2014 年一共接待 392 万游客，其中上半年接待的游客数占全年的
季度接待的游客数是上半年的
【解析】
392
3 3
7 4
126
(万人)
3
4
，第三季度接待游客多少万人?
3
7
，第三
答：第三季度接待游客 126 万人。
3.一个正方体的玻璃容器棱长是 10 厘米，先给这个容器注入 4 厘米的水，再把 2 个一样的钢球
放进里面，容器的水上升了 3 厘米，一个钢球的体积是多少立方厘米?
【解析】[10×10×(4+3)-10×10×4]÷2=150(立方厘米)
答:一个钢球的体积是 150 立方厘米。
第二卷（50 分）
一、解决问题（共 30 分）
1.(3 分)“哥德巴赫猜想”是说：每个大于 2 的偶数都可以表示成两个两位质数的和，问:168
是哪两个两位质数的和，并且其中一个质数的个位是 1?
【解析】168 是两个两位质数的和,则其中一个较小的质数定大于 68,而大于 68 的两位质数且
满足个位是 1 的只有 71。
答:168 是 71 和 97 的和。
2.(17 分)下面是小明家十一月份支出及储蓄情况统计图。
(1)(3 分)小明家十一月份的伙食共花了 1200 元，小明家的储蓄是多少元
【解析】(1)1200÷40%×25%=750(元)
答:小明家的储蓄是 750 元。
(2)(10 分)根据扇形统计图，把下表填完整
伙食费
1200
40%
项目
费用/元
百分比/%
(3)(2 分)伙食费比购物多（ 100 ）％
(4)(2 分)水电费比购物少（ 50 ）％
购物
600
20%
水电费
300
10%
储蓄
750
25%
其他支出
150
5%
总计
3000
100%
3.(5 分)小明已经进行了 20 场比赛，并且胜率为 95%。若以后一场都不输，他还需要赢几场比
赛，才能使胜率达到 96%?
【解析】设还需 x场比赛,才能使胜率达到 96%。
20 95
20
x
x
x
96
5
答：还需 5 场比赛,才能使胜率达到 96%。
4.(5 分)一辆汽车从甲地向乙地行驶，行了一段距离后，距离乙地还有 210 千米，接着又行了全
程距离的 20%，此时已行驶的距离与未行驶的距离比为 3:2，求甲、乙两地的距离。
【解析】全程＝
210
20
2
5
＝350（千米）
答：甲、乙两地相距 350 千米。
二、附加题(20 分)
1.(4 分)图中大小正方形的边长分别是 9 厘米和 5 厘米，求阴影部分的面积。
【解析】因为 AB:(AB+EC)=9:14，所以 BF:BE=9:14
故 BF＝
9
14
5
DF=DB-BF=
9
S
AFD
S
CDE
答:阴影部分面积是
45
14
45
14
81
14
81
9
14
136
28
平方厘米。
5 4
1
2
1
2
36
1
28
(平方厘米)
2.(3 分)小玲和小华姐弟俩正要从公园门口沿马路向东去某地，而他们的家要从公园门口沿马路
往西。小华问姐姐:“是先向西回家取了自行车，再骑车向东去，还是直接从公园门口步行向东
去快”?姐姐算了一下说:“如果骑车与步行的速度比是 4:1，那么从公园门口到目的地的距离超
过 2 千米时，回家取车才合算。”请推算一下，从公园到他们家的距离是多少米?
【解析】2 千米=200 米
设公园门口到家有 x米。
(2000+x)÷4=2000-x
x=1200
答：从公园到他们家的距离是 1200 米。
3.(13 分)某中学计划建设一个 400，米跑道的运动场(如图所示)，聘请你任工程师，问：
(1)若直道长 100 米，则弯道弧长半径 r 为多少米？
(2)共 8 个跑道，每条宽 1.2 米，操场最外圈长多少米?
(3)若操场中心铺绿草，跑道铺塑胶，则各需绿草、塑胶多少平
方米？
(4)若绿草 50 元/平方米，塑胶 350 元平方米，学校现有 200 万
元?可以开工吗，为什么?
【解析】（1）
r
400 100 2
2
31.8
（米）
(2)最外圈的半径=最内圈的半径+8×每条跑道的宽度
=31.8+8×1.2
=41.4(米)
最外圈长度=100×2+2×T×41.4=460 米。
(3)绿草=100×31.8×2+×31.8×31.8≈9535(平方米)
塑胶=100×41.4×2+×41.4×41.4-9535=4127(平方米)
(4)50×9535+4127×350=476750+1444450=1921200 元<200 万元,可以开工
答:(1)弯道弧长半径 r 为 31.8 米。
(2)操场最外圈长 460 米。
(3)绿草需 9535 平方米，塑胶需 4127 平方米。
(4)可以开工,造价为 1921200 元,小于现有资金。
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
