第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
模式识别作业.docx
第一部分：计算与证明 ：
1.
2.
第二部分：计算机编程
1.
2.
3.
第一部分：计算与证明 ：
1.
现有四个来自于两个类别的二维空间中的样本，其中第一类的两个样本为
(1,4)T 和 (2,3)T ，第二类的两个样本为 (4,1)T 和 (3,2)T 。这里，上标T表示向量转
置。若采用规范化增广样本表示形式，并假设初始的权向量 a
(0,1,0)T
，其中向
量 a 的第三维对应于样本的齐次坐标。同时，假定梯度更新步长
k 固定为1。
1
试利用批处理感知器算法求解线性判别函数 (y)
范化增广样本表示”是指对齐次坐标表示的样本进行规范化处理）。
a yT
g
的权向量 a 。（注：“规
解：最小化准则函数：
min
a
J
p
(a)
y
Y
( a y)T
，其中，Y 为错分样本集合。
考察 ( )
pJ a
对 a
的导数，得：
(a)
J
p
a
根据梯度下降法，更新准则如下： 1
k
a
y
y
Y
a
k
k
y
Y
k
y
1
1
2
=(x ,x ) {(1,4) ,(2,3) }, =(x ,x ) {(4,1) ,(3,2) }
T
T
T
T
2
3
4
四个样本的规范化增广样本向量为：
y =(1,4,1) , y
1
T
2
(2,3,1) ,y
T
3
( 4, 1, 1) , y
T
( 3, 2, 1)
T
4
初始权向量 1a
1 第一次迭代：
(0,1,0)T
，梯度更新步长
k
1
a
T
1
a
T
1
y =(0,1,0) (1,4,1) =4 0
＞
1
T
y =(0,1,0) (2,3,1) =3 0
＞
2
T
a
T
1
a
T
1
修正后的权向量为：
y =(0,1,0) ( 4, 1, 1) = 1 0
＜
3
T
y =(0,1,0) ( 3, 2, 1) = 2 0
＜
4
T
a
2
a
1
2 第二次迭代：
y +y =(0,1,0) +( 4, 1, 1) +( 3, 2, 1) =( 7, 2, 2)
T
3
T
T
T
4
y =( 7, 2, 2) (1,4,1) = 17 0
＜
1
T
#03
y =( 7, 2, 2) (2,3,1) = 22 0
＜
2
T
y =( 7, 2, 2) ( 4, 1, 1) =32 0
＞
3
T
a
T
2
a
T
2
a
T
2
a
T
2
y =( 7, 2, 2) ( 3, 2, 1) =27 0
＞
4
T
修正后的权向量为：
a
3
a
2
3 第三次迭代：
y +y =( 7, 2, 2) +(1,4,1) +(2,3,1) =( 4,5,0)
T
1
T
T
T
2
a
T
3
y =( 4,5,0) (1,4,1) =16 0
＞
1
T
a
T
3
y =( 4,5,0) (2,3,1) =7 0
＞
2
T
a
T
3
a
T
3
y =( 4,5,0) ( 4, 1, 1) =11 0
＞
3
T
y =( 4,5,0) ( 3, 2, 1) =2 0
＞
4
T
至此迭代结束，最终的权向量为 3
a=a =( 4,5,0)T
，保证所有样本线性可分。
2.
对于多类分类情形，考虑one-vs-all 技巧，即构建 c 个线性判别函数：
g
i
(x) w x+
T
i
0
i
,
i
1,2,...,
c
此时的决策规则为：对 j
i ，如果 (x)
g
g＞
i
(x)
j
, x 则被分为 i类。现有三个
二维空间内的模式分类器，其判别函数为：
g
1
(x)
x
1
x
2
g
2
(x)
x
1
x
2
1
g
3
(x)
x
2
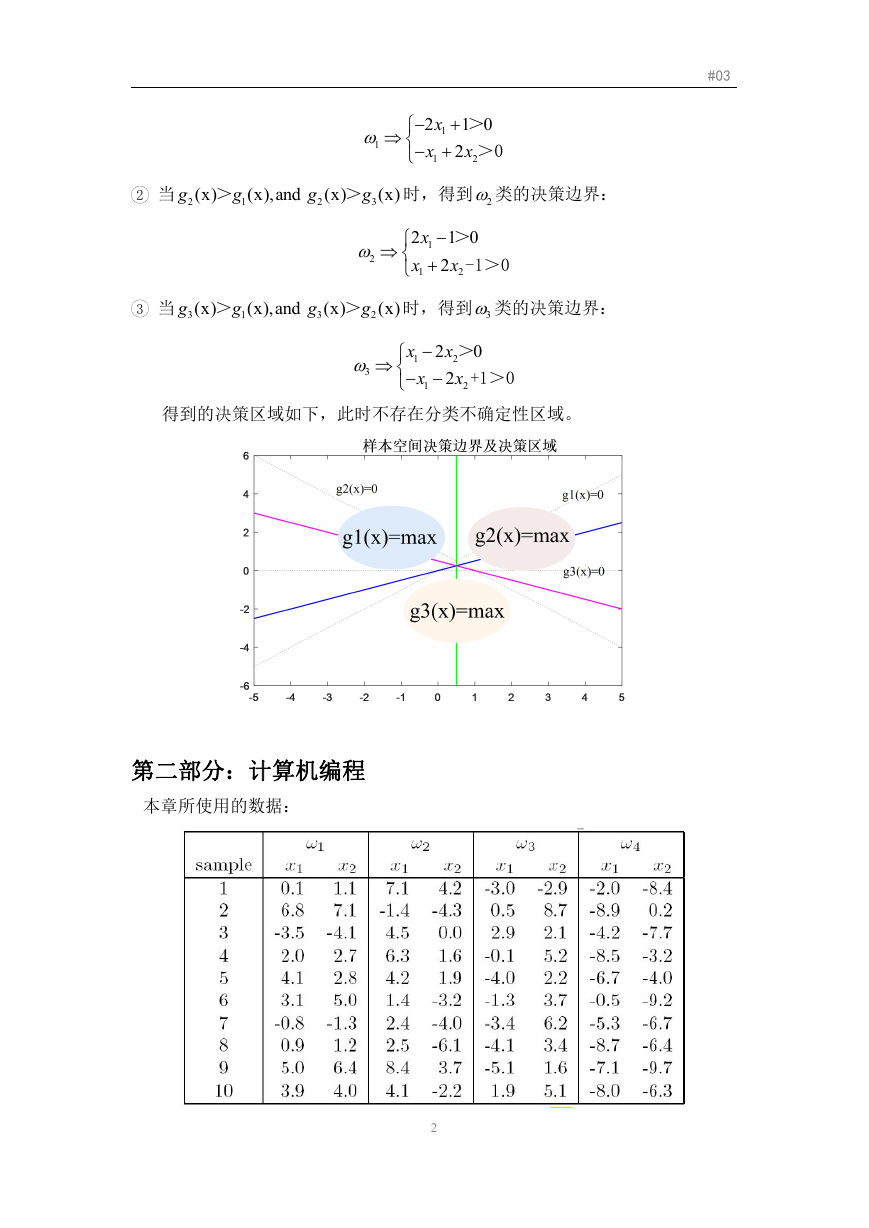
试画出决策面，指出为何此时不存在分类不确定性区域。
解：根据决策规则：
g
1 当 1
(x)
g
＞
(x),and
g
1
2
(x)
g
＞
3
(x)
时，得到 1类的决策边界：
1
1
1 0
2
x
＞
1
2
x
x
＞0
2
1
g
2 当 2
(x)
g
＞
1
(x),and
g
(x)
g
＞
(x)
3
2
时，得到 2 类的决策边界：
#03
2
g
3 当 3
(x)
g
＞
1
(x),and
g
(x)
g
＞
2
3
1 0
2
x
＞
1
2
x
x
1
2
(x)
-1＞0
时，得到 3 类的决策边界：
3
2
x
1
x
1
0
x
＞
2
2
x
+1＞0
2
得到的决策区域如下，此时不存在分类不确定性区域。
第二部分：计算机编程
本章所使用的数据：
2
#03
1.
编写程序以实现“批处理感知”算法。
(a) 从 a = 0 开始，将程序应用于 1和 2 中的训练数据。 请指出收敛所需的迭代
数（即记录收敛的步骤数）。
(b) 将你的程序应用于来自 3 和 2 的训练数据。 再次指出收敛所需的迭代次数。
解：
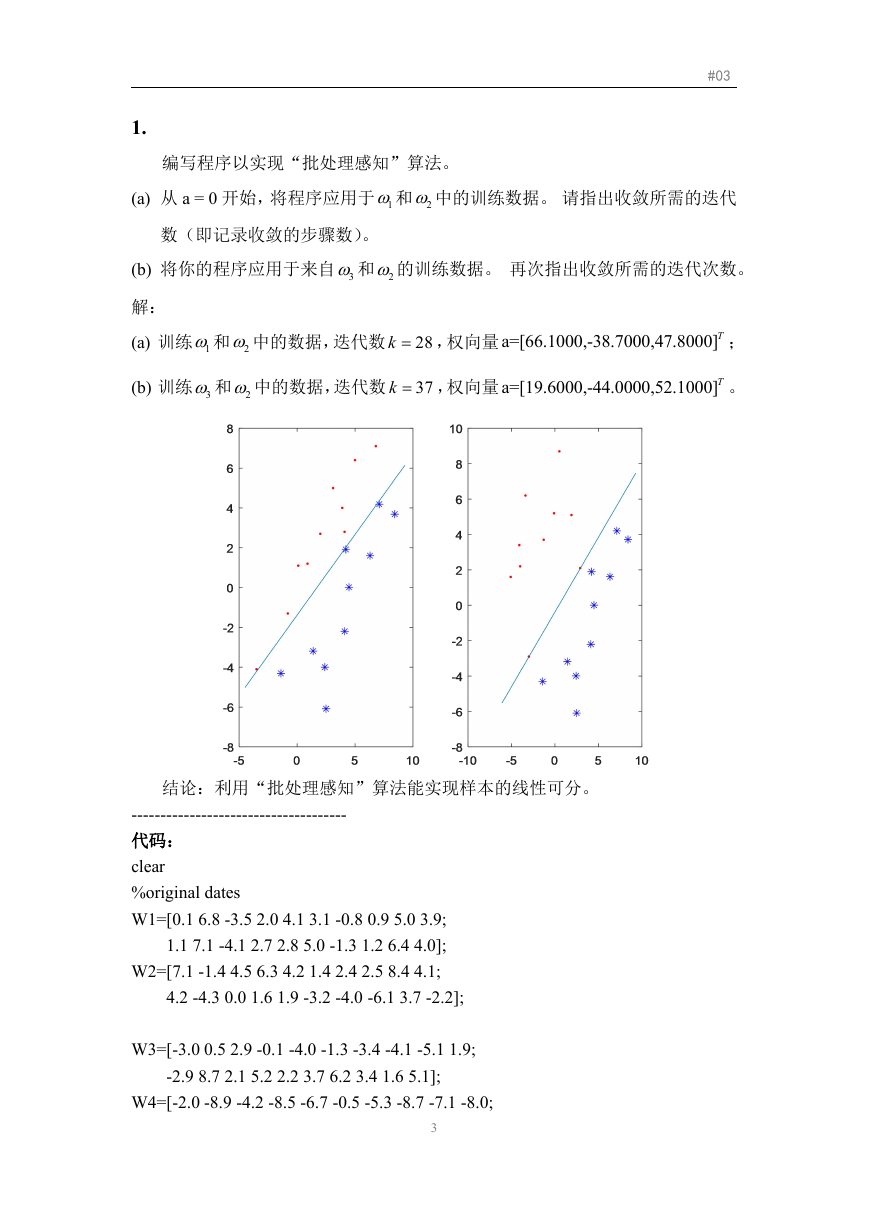
(a) 训练 1和 2 中的数据，迭代数 28
k ，权向量 a=[66.1000,-38.7000,47.8000]T ；
(b) 训练 3 和 2 中的数据，迭代数 37
k ，权向量 a=[19.6000,-44.0000,52.1000]T 。
结论：利用“批处理感知”算法能实现样本的线性可分。
-------------------------------------
代码：
clear
%original dates
W1=[0.1 6.8 -3.5 2.0 4.1 3.1 -0.8 0.9 5.0 3.9;
1.1 7.1 -4.1 2.7 2.8 5.0 -1.3 1.2 6.4 4.0];
W2=[7.1 -1.4 4.5 6.3 4.2 1.4 2.4 2.5 8.4 4.1;
4.2 -4.3 0.0 1.6 1.9 -3.2 -4.0 -6.1 3.7 -2.2];
W3=[-3.0 0.5 2.9 -0.1 -4.0 -1.3 -3.4 -4.1 -5.1 1.9;
-2.9 8.7 2.1 5.2 2.2 3.7 6.2 3.4 1.6 5.1];
W4=[-2.0 -8.9 -4.2 -8.5 -6.7 -0.5 -5.3 -8.7 -7.1 -8.0;
3
#03
-8.4 0.2 -7.7 -3.2 -4.0 -9.2 -6.7 -6.4 -9.7 -6.3];
%将所有训练样本进行规范化增广
ww1=[ones(1, size(W1, 2));W1];
ww2=[ones(1, size(W2, 2));W2];
ww3=[ones(1, size(W3, 2));W3];
%对 W1、W2 训练
w12=[ww1,-ww2];%增广样本规范化为 w12
y=zeros(1,size(w12,2));%y 初始为零矩阵
a=[0;0;0];%初始权向量 a
k=0;
while any(y<=0)
for i=1: size(y, 2)
y(i)=a'*w12(:,i);
end;
a=a+(sum((w12(:,find(y<=0)))'))';%修正向量 a
k=k+1;%收敛步数
end;
subplot(1, 2, 1);
plot(W1(1,:),W1(2,:),'r.');
hold on;
plot(W2(1,:),W2(2,:), 'b*');
%找到样本在坐标中的集中区域，以便于打印样本坐标图
xmin=min(min(W1(1,:)) ,min(W2(1,:)));
xmax=max(max(W1(1,:)) ,max(W2(1,:)));
xindex=xmin-1: (xmax-xmin)/100: xmax+1;
yindex=-a(2)*xindex/a(3)-a(1)/a(3);
plot(xindex, yindex);
%对 W3、W2 训练
w32=[ww3,-ww2];%增广样本规范化为 w32
y=zeros(1,size(w32,2));%y 初始为零矩阵
a=[0;0;0];%初始权向量 a
k=0;
while any(y<=0)
for i=1: size(y,2)
y(i)=a'*w32(:,i);
4
#03
end;
a=a+(sum((w32(:,find(y<=0)))'))';%修正向量 a
k=k+1;%收敛步数
end;
subplot(1,2,2);
plot(W3(1,:),W3(2,:),'r.');
hold on;
plot(W2(1,:),W2(2,:), 'b*');
%找到样本在坐标中的集中区域，以便于打印样本坐标图
xmin=min(min(W3(1,:)) ,min(W2(1,:)));
xmax=max(max(W3(1,:)) ,max(W2(1,:)));
xindex=xmin-1: (xmax-xmin)/100: xmax+1;
yindex=-a(3)*xindex/a(2)-a(1)/a(2);
plot(xindex, yindex);
2.
编写 Ho-Kashyap 算法并应用到 1和 3 数据上，再应用到 2 和 4 数据上，
指出并分析训练误差。
(1)
1和 3 数据
loss: [0,0,0,0,0.011,0,0,0.013,0,0,0,0,0,0,0.5303,0,0.7142,0.613,0.6022,0]
分析：经过 2 次迭代，大部分样本的 loss 下降到 0，少部分的点和超平面的
MSE 值很大，导致 all_loss 很大，这部分点是各类别中远离分界面的边缘点。
(2)
2 和 4 数据
loss:[0.02,0,0.131,0.0165, 0.0146, 0.0066, 0.0068, 0.0048, 0.0208, 0.0105,
0.0022,0, 0.0038, 0.0038, 0.0027,0, 0.004, 0.0072, 0.0088, 0.0064]
5
#03
分析：两类数据的点集中于分界面附近，总体 MSE 很小，但需要增加迭代
次数才能逐步降低训练误差。此时得到 MSE 的解可能并不收敛于可分超平面。
-------------------------------------
代码：
import numpy.linalg
[6.8,7.1,1.0],
x
[-3.5,-4.1,1.0],[2.0,2.7,1.0],[4.1,2.8,1.0],[3.1,5.0,1.0],[-0.8,-1.3,1.0],[0.9,1.2,1.0],[5.0,
6.4,1.0],[3.9,4.0,1.0],
numpy.array([[0.1,1.1,1.0],
=
[3.0,2.9,-1.0],
[-0.5,-8.7,-1.0],[-2.9,-2.1,-1.0],[0.1,-5.2,-1.0],[4.0,-2.2,-1.0],[1.3,-3.7,-1.0],[3.4,-6.2,-1.
0],[4.1,-3.4,-1.0],[5.1,-1.6,-1.0],[-1.9,-5.1,-1.0]]) # Example one, solution is possible
#
=
numpy.array([[7.1,4.2,1.0],[-1.4,-4.3,1.0],[4.5,0.0,1.0],[6.3,1.6,1.0],[4.2,1.9,1.0],[1.4,-
3.2,1.0],[2.4,-4.0,1.0],[2.5,-6.1,1.0],[8.4,3.7,1.0],[4.1,-2.2,1.0],
x
#[2.0,8.4,-1.0],[8.9,-0.2,-1.0],[4.2,7.7,-1.0],[8.5,3.2,-1.0],[6.7,4.0,-1.0],[0.5,9.2,-1.0],[
5.3,6.7,-1.0],[8.7,6.4,-1.0],[7.1,9.7,-1.0],[8.0,6.3,-1.0]])
def findE(x, b, W, lr): # Function to find the matrix "E"
E = numpy.subtract(numpy.dot(x,W), b) # Subtract b from x times W
E_PLUS = 0.5 * (numpy.array(E) + numpy.abs(E))
E_PLUS = numpy.around(E_PLUS.astype(numpy.double), 4) # Round the E
matrix to one decimal point,将 E 矩阵四舍五入到小数点后一位
b = numpy.array(b) + 2 * lr * numpy.array(E_PLUS)
x_inv = numpy.linalg.pinv(x) # Find the Moore-Penrose Inverse of x
W = numpy.dot(x_inv, b) # Multiple x# and b
return E_PLUS, b, W
def cal_all_loss(E):
all_loss = 0
for l in E:
all_loss = all_loss + numpy.power(l[0],2)#第一行的所有元素，计算平方误
差
return all_loss
def __main__():
b = numpy.array([0.1 for x in range(20)]).reshape((20, 1))
W = numpy.array([0.5 for x in range(3)]).reshape((3, 1))
6
b_min = numpy.array([0.02 for x in range(20)]).reshape((20, 1))
k_max = 25
lr = 0.5
#03
for k in range(k_max):
E, b, W = findE(x,b, W , lr)
all_loss = cal_all_loss(E)
#all_loss.append(cal_all_loss(E))
if (numpy.abs(E).tolist() <= b_min.tolist()):
print("k:",k)
print("b", b)
print("W:",W)
print("loss:",E)
break
print(k,"次迭代 all_loss:",all_loss)
__main__()
3.
请写一个程序，实现MSE多类扩展方法。每一类用前8个样本来构造分类器，
用后两个样本作测试。请给出你的正确率。
-------------------------------------
代码：
# *-coding:utf-8-*
import numpy as np
#数据
w1 = [
[0.1,1.1],
[6.8,7.1],
[-3.5,-4.1],
[2.0, 2.7],
[4.1, 2.8],
7
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
