第1页 / 共260页
第2页 / 共260页
第3页 / 共260页
第4页 / 共260页
第5页 / 共260页
第6页 / 共260页
第7页 / 共260页
第8页 / 共260页
Probability, Statistics, and Random Processes for Engineers Solution Manual.pdf
Solutions Manual for
Probability and Random Processes for
Electrical and Computer Engineers
John A. Gubner
University of Wisconsin–Madison
File Generated July 13, 2007
CHAPTER 1
Problem Solutions
1. Ω = {1, 2, 3, 4, 5, 6}.
2. Ω = {0, 1, 2, . . . , 24, 25}.
3. Ω = [0, ∞). RTT > 10 ms is given by the event (10, ∞).
4.
5.
(a) Ω = {(x, y) ∈ IR2 : x2 + y2 ≤ 100}.
(b) {(x, y) ∈ IR2 : 4 ≤ x2 + y2 ≤ 25}.
(a) [2, 3]c = (−∞, 2)∪ (3, ∞).
(b) (1, 3)∪ (2, 4) = (1, 4).
(c) (1, 3)∩ [2, 4) = [2, 3).
(d) (3, 6]\ (5, 7) = (3, 5].
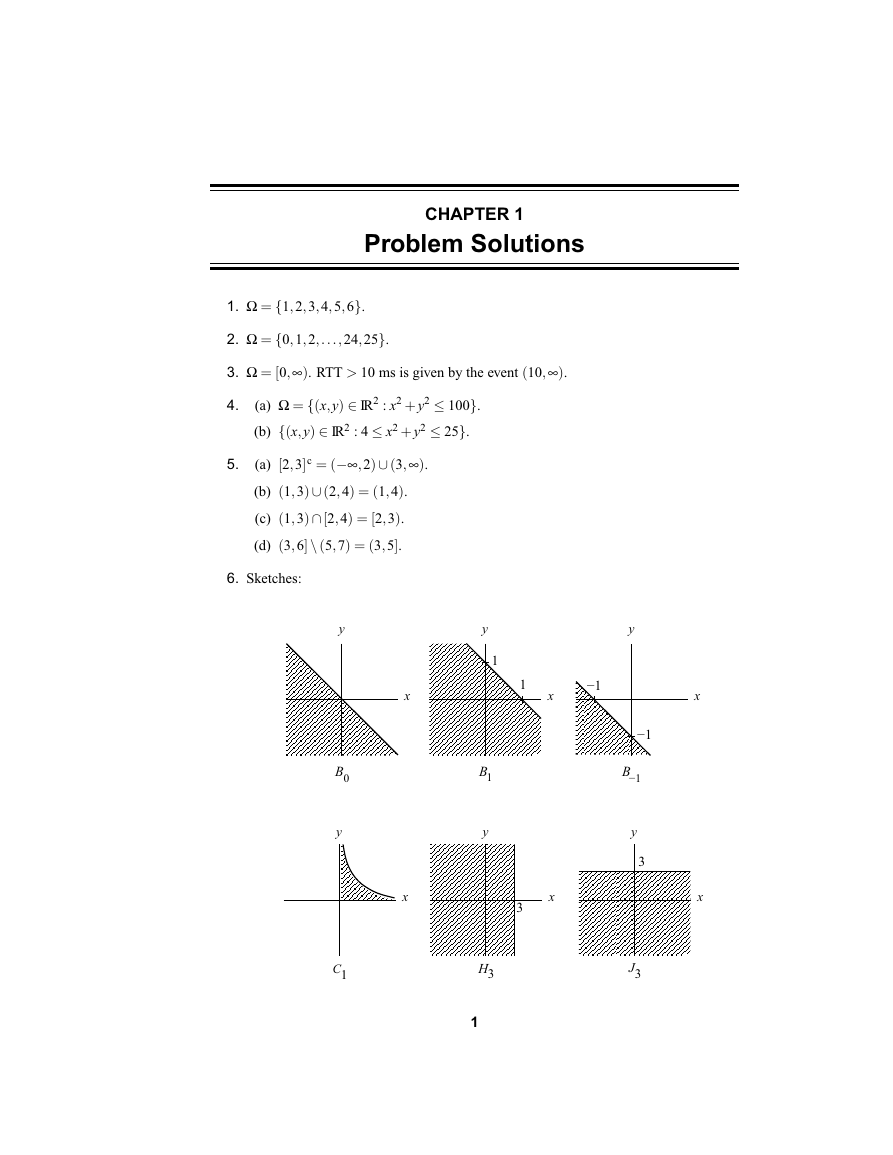
6. Sketches:
y
B
0
y
C1
x
x
1
x
−1
x
3
y
−1
B
−1
y
3
J3
x
x
y
1
1B
y
H3
1
2
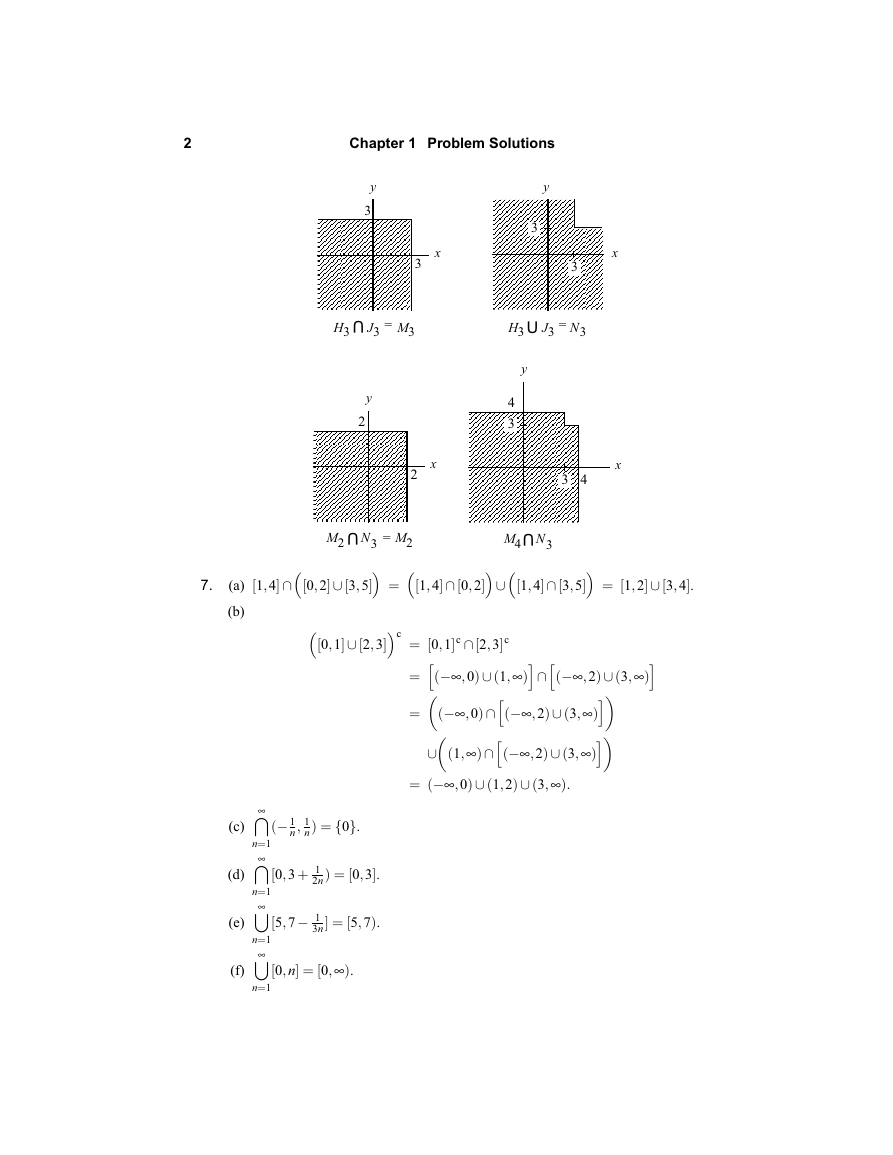
Chapter 1 Problem Solutions
y
3
y
3
x
3
x
3
H3
U = M3
J3
UH3
=
J3 N3
y
2
y
4
3
x
2
x
3
4
2M
U = 2M
N3
4M N3U
7.
(a) [1, 4]∩[0, 2]∪ [3, 5] = [1, 4]∩ [0, 2]∪[1, 4]∩ [3, 5] = [1, 2]∪ [3, 4].
(b)
[0, 1]∪ [2, 3]c
= [0, 1]c ∩ [2, 3]c
= h(−∞, 0)∪ (1, ∞)i∩h(−∞, 2)∪ (3, ∞)i
= (−∞, 0)∩h(−∞, 2)∪ (3, ∞)i
∪(1, ∞)∩h(−∞, 2)∪ (3, ∞)i
= (−∞, 0)∪ (1, 2)∪ (3, ∞).
n , 1
n ) = {0}.
2n ) = [0, 3].
3n ] = [5, 7).
(c)
(d)
(e)
(f)
[0, 3 + 1
∞\n=1
(− 1
∞\n=1
∞[n=1
[5, 7− 1
∞[n=1
[0, n] = [0, ∞).
Chapter 1 Problem Solutions
3
8. We first let C ⊂ A and show that for all B, (A∩ B)∪C = A∩ (B∪C). Write
A∩ (B∪C) = (A∩ B)∪ (A∩C),
by the distributive law,
= (A∩ B)∪C,
since C ⊂ A ⇒ A∩C = C.
For the second part of the problem, suppose (A∩ B)∪C = A∩ (B∪C). We must show
that C ⊂ A. Let ω ∈ C. Then ω ∈ (A ∩ B) ∪ C. But then ω ∈ A ∩ (B ∪ C), which
implies ω ∈ A.
9. Let I := {ω ∈ Ω : ω ∈ A ⇒ ω ∈ B}. We must show that A∩ I = A∩ B.
⊂: Let ω ∈ A∩ I. Then ω ∈ A and ω ∈ I. Therefore, ω ∈ B, and then ω ∈ A∩ B.
⊃: Let ω ∈ A∩ B. Then ω ∈ A and ω ∈ B. We must show that ω ∈ I too. In other
words, we must show that ω ∈ A ⇒ ω ∈ B. But we already have ω ∈ B.
10. The function f : (−∞, ∞) → [0, ∞) with f (x) = x3 is not well defined because not all
values of f (x) lie in the claimed co-domain [0, ∞).
11.
12.
(a) The function will be invertible if Y = [−1, 1].
(b) {x : f (x) ≤ 1/2} = [−π/2,π/6].
(c) {x : f (x) < 0} = [−π/2, 0).
(a) Since f is not one-to-one, no choice of co-domain Y can make f : [0,π] → Y
invertible.
(b) {x : f (x) ≤ 1/2} = [0,π/6]∪ [5π/6,π].
(c) {x : f (x) < 0} = ∅.
13. For B ⊂ IR,
f −1(B) =
X, 0 ∈ B and 1 ∈ B,
A, 1 ∈ B but 0 /∈ B,
Ac, 0 ∈ B but 1 /∈ B,
∅, 0 /∈ B and 1 /∈ B.
14. Let f : X → Y be a function such that f takes only n distinct values, say y1, . . . , yn.
Let B ⊂ Y be such that f −1(B) is nonempty. By definition, each x ∈ f −1(B) has the
property that f (x) ∈ B. But f (x) must be one of the values y1, . . . , yn, say yi. Now
f (x) = yi if and only if x ∈ Ai := f −1({yi}). Hence,
f −1(B) = [i:yi∈B
Ai.
15.
(a) f (x) ∈ Bc ⇔ f (x) /∈ B ⇔ x /∈ f −1(B) ⇔ x ∈ f −1(B)c.
(b) f (x) ∈
Bn if and only if f (x) ∈ Bn for some n; i.e., if and only if x ∈ f −1(Bn)
∞[n=1
for some n. But this says that x ∈
f −1(Bn).
∞[n=1
4
Chapter 1 Problem Solutions
Bn if and only if f (x) ∈ Bn for all n; i.e., if and only if x ∈ f −1(Bn)
(c) f (x) ∈
∞\n=1
for all n. But this says that x ∈
f −1(Bn).
∞\n=1
is countable.
16. If B =Si{bi} and C =Si{ci}, put a2i := bi and a2i−1 := ci. Then A =Si ai = B∪ C
17. Since each Ci is countable, we can write Ci =S j ci j. It then follows that
B :=
Ci =
∞[i=1
∞[i=1
∞[j=1{ci j}
is a doubly indexed sequence and is therefore countable as shown in the text.
If B = ∅, we’re done by definition. Otherwise, there is at least one element of B in
18. Let A =Sm{am} be a countable set, and let B ⊂ A. We must show that B is countable.
A, say ak. Then put bn := an if an ∈ B, and put bn := ak if an /∈ B. ThenSn{bn} = B
19. Let A ⊂ B where A is uncountable. We must show that B is uncountable. We prove
this by contradiction. Suppose that B is countable. Then by the previous problem, A
is countable, contradicting the assumption that A is uncountable.
and we see that B is countable.
20. Suppose A is countable and B is uncountable. We must show that A∪B is uncountable.
We prove this by contradiction. Suppose that A ∪ B is countable. Then since B ⊂
A ∪ B, we would have B countable as well, contradicting the assumption that B is
uncountable.
21. MATLAB. OMITTED.
22. MATLAB. Intuitive explanation: Using only the numbers 1, 2, 3, 4, 5, 6, consider how
many ways there are to write the following numbers:
1 way,
2 = 1 + 1
2 ways,
3 = 1 + 2 = 2 + 1
3 ways,
4 = 1 + 3 = 2 + 2 = 3 + 1
4 ways,
5 = 1 + 4 = 2 + 3 = 3 + 2 = 4 + 1
6 = 1 + 5 = 2 + 4 = 3 + 3 = 4 + 2 = 5 + 1
5 ways,
7 = 1 + 6 = 2 + 5 = 3 + 4 = 4 + 3 = 5 + 2 = 6 + 1 6 ways,
5 ways,
8 = 2 + 6 = 3 + 5 = 4 + 4 = 5 + 3 = 6 + 2
4 ways,
9 = 3 + 6 = 4 + 5 = 5 + 4 = 6 + 3
3 ways,
2 ways,
1 way,
36 ways, 36/36 = 1
1/36 = 0.0278
2/36 = 0.0556
3/36 = 0.0833
4/36 = 0.1111
5/36 = 0.1389
6/36 = 0.1667
5/36 = 0.1389
4/36 = 0.1111
3/36 = 0.0833
2/36 = 0.0556
1/36 = 0.0278
10 = 4 + 6 = 5 + 5 = 6 + 4
11 = 5 + 6 = 6 + 5
12 = 6 + 6
23. Take Ω := {1, . . . , 26} and put
P(A) := |A|
|Ω|
= |A|
26
.
Chapter 1 Problem Solutions
5
The event that a vowel is chosen is V = {1, 5, 9, 15, 21}, and P(V ) = |V|/26 = 5/26.
24. Let Ω := {(i, j) : 1 ≤ i, j ≤ 26 and i 6= j}. For A ⊂ Ω, put P(A) := |A|/|Ω|. The event
that a vowel is chosen followed by a consonant is
Similarly, the event that a consonant is followed by a vowel is
Bvc = (i, j) ∈ Ω : i = 1, 5, 9, 15, or 21 and j ∈ {1, . . . , 26}\{1, 5, 9, 15, 21}.
Bcv = (i, j) ∈ Ω : i ∈ {1, . . . , 26}\{1, 5, 9, 15, 21} and j = 1, 5, 9, 15, or 21.
P(Bvc ∪ Bcv) = |Bvc| +|Bcv|
5· (26− 5) + (26− 5)· 5
21
65 ≈ 0.323.
We need to compute
=
|Ω|
650
=
The event that two vowels are chosen is
Bvv = (i, j) ∈ Ω : i, j ∈ {1, 5, 9, 15, 21} with i 6= j,
and P(Bvv) = |Bvv|/|Ω| = 20/650 = 2/65 ≈ .031.
25. MATLAB. The code for simulating the drawing of a face card is
% Simulation of Drawing a Face Card
%
n = 10000;
X = ceil(52*rand(1,n));
faces = (41 <= X & X <= 52);
nfaces = sum(faces);
fprintf(’There were %g face cards in %g draws.\n’,nfaces,n)
% Number of draws.
26. Since 9 pm to 7 am is 10 hours, take Ω := [0, 10]. The probability that the baby wakes
up during a time interval 0 ≤ t1 < t2 ≤ 10 is
P([t1,t2]) := Z t2
t1
1
10
dω.
Hence, P([2, 10]c) = P([0, 2]) =R 2
27. Starting with the equations
0 1/10 dω = 1/5.
SN = 1 + z + z2 +··· + zN−2 + zN−1
zSN =
z + z2 +··· + zN−2 + zN−1 + zN,
subtract the second line from the first. Canceling common terms leaves
SN − zSN = 1− zN,
or
SN(1− z) = 1− zN.
If z 6= 1, we can divide both sides by 1− z to get SN = (1− zN)/(1− z).
6
Chapter 1 Problem Solutions
28. Let x = p(1). Then p(2) = 2p(1) = 2x, p(3) = 2p(2) = 22x, p(4) = 2p(3) = 23x,
p(5) = 24x, and p(6) = 25x. In general, p(ω) = 2ω−1x and we can write
1 =
6
∑
ω=1
p(ω) =
6
∑
ω=1
2ω−1x = x
5
∑
ω=0
2ω =
1− 26
1− 2
x = 63x.
Hence, x = 1/63, and p(ω) = 2ω−1/63 for ω = 1, . . . , 6.
(a) By inclusion–exclusion, P(A∪ B) = P(A) + P(B)− P(A∩ B), which can be re-
29.
arranged as P(A∩ B) = P(A) + P(B)− P(A∪ B).
(b) Since P(A) = P(A∩ B) + P(A∩ Bc),
P(A∩ Bc) = P(A)− P(A∩ B) = P(A∪ B)− P(B),
by part (a).
(c) Since B and A∩ Bc are disjoint,
P(B∪ (A∩ Bc)) = P(B) + P(A∩ Bc) = P(A∪ B),
by part (b).
(d) By De Morgan’s law, P(Ac ∩ Bc) = P([A∪ B]c) = 1− P(A∪ B).
30. We must check the four axioms of a probability measure. First,
P(∅) = λP1(∅) + (1−λ)P2(∅) = λ· 0 + (1−λ)· 0 = 0.
Second,
Third,
P(A) = λP1(A) + (1−λ)P2(A) ≥ λ· 0 + (1−λ)· 0 = 0.
P ∞[n=1
An = λP1 ∞[n=1
An + (1−λ)P2 ∞[n=1
An
= λ
∞
∑
n=1
P1(An) + (1−λ)
P2(An)
∞
∑
n=1
=
=
∞
∑
n=1
[λP1(An) + (1−λ)P2(An)]
∞
∑
n=1
P(An).
Fourth, P(Ω) = λP1(Ω) + (1−λ)P2(Ω) = λ + (1−λ) = 1.
31. First, since ω0 /∈ ∅, µ(∅) = 0. Second, by definition, µ(A) ≥ 0. Third, for disjoint
An, suppose ω0 ∈Sn An. Then ω0 ∈ Am for some m, and ω0 /∈ An for n 6= m. Then
µ(Am) = 1 and µ(An) = 0 for n 6= m. Hence, µSn An = 1 and ∑n µ(An) = µ(Am) =
1. A similar analysis shows that if ω0 /∈Sn An then µSn An and ∑n µ(An) are both
zero. Finally, since ω0 ∈ Ω, µ(Ω) = 1.
Chapter 1 Problem Solutions
7
32. Starting with the assumption that for any two disjoint events A and B, P(A ∪ B) =
P(A) + P(B), we have that for N = 2,
Now we must show that if (∗) holds for any N ≥ 2, then (∗) holds for N + 1. Write
P(An).
(∗)
P N+1[n=1
N
∑
n=1
An =
P N[n=1
An = P N[n=1
An∪ AN+1
= P N[n=1
An + P(AN+1),
P(An) + P(AN+1),
=
=
N
∑
n=1
N+1
∑
n=1
P(An).
additivity for two events,
by (∗),
33. Since An := Fn ∩ F c
n−1 ∩···∩ F c
1 ⊂ Fn, it is easy to see that
N[n=1
An ⊂
Fn.
N[n=1
The hard part is to show the reverse inclusion ⊃. Suppose ω∈SN
n=1 Fn. Then ω∈ Fn
for some n in the range 1, . . . , N. However, ω may belong to Fn for several values of
n since the Fn may not be disjoint. Let
k := min{n : ω ∈ Fn and 1 ≤ n ≤ N}.
In other words, 1 ≤ k ≤ N and ω ∈ Fk, but ω /∈ Fn for n < k; in symbols,
Hence, ω ∈ Ak ⊂SN
k := min{n : ω ∈ Fn and n ≥ 1}.
k−1 ∩···∩ F c
n=1 An. The proof thatS∞
n=1 An ⊂S∞
ω ∈ Fk ∩ F c
1 =: Ak.
n=1 Fn is similar except that
34. For arbitrary events Fn, let An be as in the preceding problem. We can then write
P ∞[n=1
Fn = P ∞[n=1
An =
∞
∑
n=1
P(An),
since the An are disjoint,
= lim
N→∞
= lim
N→∞
= lim
N→∞
P(An),
by def. of infinite sum,
N
∑
n=1
P N[n=1
P N[n=1
An
Fn.
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
