一种基于LBM的气液固三相流多尺度模拟方法 .pdf

发布时间：2022-06-14 发布人：admin 分类：说明书资料大小：0.53M 资料格式：pdf 举报版权申诉

f13c5600-165c-4cd3-8eab-2246823629d6.pdf-第1页.png

第1页 / 共7页

f13c5600-165c-4cd3-8eab-2246823629d6.pdf-第2页.png

第2页 / 共7页

f13c5600-165c-4cd3-8eab-2246823629d6.pdf-第3页.png

第3页 / 共7页

f13c5600-165c-4cd3-8eab-2246823629d6.pdf-第4页.png

第4页 / 共7页

f13c5600-165c-4cd3-8eab-2246823629d6.pdf-第5页.png

第5页 / 共7页

f13c5600-165c-4cd3-8eab-2246823629d6.pdf-第6页.png

第6页 / 共7页

f13c5600-165c-4cd3-8eab-2246823629d6.pdf-第7页.png

第7页 / 共7页

文本预览

http://www.paper.edu.cn 一种基于 LBM 的气液固三相流多尺度模拟方法刘马林1 王铁峰于伟王金福（清华大学化学工程系绿色反应工程与工艺北京市重点实验室，北京，100084）摘要：本文阐述了 LBM 在气液固三相流领域的多尺度模拟方法及实现过程，宏观尺度的 LBM 双流体模型，介观尺度的气泡动力学模拟和颗粒动力学模拟，并给出了典型的模拟结果，探讨了介观尺度上单气泡和单颗粒在流场中的运动行为，在此过程中凸现了 LBM 在介观（气泡/颗粒）尺度的模拟优势：格子玻耳兹曼方法可以在介观尺度上对气泡和颗粒行为进行准确描述。本文发现，通过相间作用力可将介观尺度模拟和宏观格子玻耳兹曼双流体模型进行尺度间耦合，从而形成多尺度[宏观尺度（gas/liquid/solid）＋介观尺度(bubble/fluid/particle)]的气液固三相流模拟平台，可以预见，在此耦合模型基础上对多相流进行多尺度的研究将有利于进一步深入认识和探讨多相流的复杂规律和机理。关键词：格子玻尔兹曼方法，多相流，多尺度，相间作用力 A multiscale simulation method for gas-liquid-solid three phase flow based on lattice Boltzmann method Malin Liu, Tiefeng Wang, Wei Yu, Jifu Wang (Department of chemical engineering, Tsinghua University, 100084, Beijing, China) Abstract: The Lattice Boltzmann Method (LBM) is a recently developed numerical scheme for simulating a variety of physical systems. LBM may arguably be classified as a mesoscopic approach for the simulation of fluid dynamics, and can be considered being between the molecular dynamics, which accesses micro-scale, but as a result suffers from severe time constraints in the investigation of hydrodynamics, and the finite-difference solution of the Navier-Stokes equations. It is a promising method which has been used broadly, including in multiphase flow modeling and simulations, because of its advantages. A multiscale simulation of the gas-liquid-solid three phase flow based on LBM was presented in this paper. A macroscale LBM two-fluid model and the mesoscale bubble dynamic model, particle dynamic model which were coupled by the interphase forces (drag force, virtual mass force and lift force) were proposed. It can be imagined that an in-depth study of the multiphase flow can be obtained by simulating and investigating with this unified model conveniently in the future. Keywords: Lattice Boltzmann method; Multiphase flow; Multiscale analysis; Interphase force. 1联系人：刘马林第一作者：刘马林(1983—)，男，博士研究生. 基金项目：国家自然科学基金（20606021, 20576060）. Corresponding author: Liu Malin. E-mail: liumalin@flotu.org，Tel:010-62794134 Foundation item: supported by the National Natural Science Foundation of China (20606021, 20576060). 1

http://www.paper.edu.cn 引言气-液、气-液-固多相反应系统涉及化工、石化、生物化工、食品化工、冶金、能源、环境工程等许多工业过程（Fan，1989）。我国石油资源重质化严重，煤炭和天然气资源相对丰富，因此重油加工过程和天然气及煤基清洁能源过程的开发对于我国能源结构的调整具有重大的战略意义，这些过程均涉及到多相流反应器的设计与应用。自从 1937 年利用浆态鼓泡床进行 Fischer-Tropsch 合成工艺的第一次实验以后，三相床反应工艺逐渐受到人们的重视。由于三相浆态床工艺的独特作用，相继在液相法甲醇合成、一步法合成二甲醚、煤直接液化、浆态加氢和液相法甲烷化等方面得到了开发与应用，并取得了显著成果。近年来随着生物化工与环境化工的兴起，对气液固三相反应体系的研究得到了人们广泛的重视，三相浆态床反应器也越来越被广泛的应用到工业实践中，对三相浆态床的研究也在蓬勃发展。目前的大多数研究多是基于宏观层次上经验和理论的结合，多采用全床平均或局部时空平均的办法，对反应器整体进行研究，其中包括多相流的流体力学行为，传质行为，扩散行为等，建立了大量的预测关联式(Liu et al, 2007a)，但已有的研究多为实验研究其流动、传质和混合行为，对其中的流动和传递机制尚缺乏深入的认识；近年来计算流体力学 (CFD: Computational Fluid Dynamics) 在气液及气液固浆态体系中得到了越来越多的应用，初步显示出这一方法的优势和潜力。文献中模拟方面的工作主要采用双流体模型，此类模型只能计算时间或空间平均化后的速度和相含率等流动参数，不能得到气泡运动、聚并和破碎等更细致的信息。双流体模型一般采用简化的相间作用关联式，只能对均匀鼓泡流动有较好的预测能力，而对于气含率或固含率较高的复杂流动，模拟结果有很大的偏差。这一局限的主要原因是在于气泡与流体以及气泡与气泡之间的相互作用紧密耦合，使得气泡受力复杂，气液相间作用项封闭困难。解决这一问题需要获得更细致的流动信息，因此，近年来一些学者开展了更基础的模拟研究，如 Li et al. (1999) 采用 VOF 方法对气液固三相体系中的气泡及其尾涡行为进行模拟，Sankaranarayanan & Sundaresan (2002) 采用 LBM(Lattice Boltzmann Method) 对气液体系中单气泡行为进行模拟，Inamuro et al. (2004) 则初步探索了 LBM 用于多气泡体系的模拟。这些模拟结果能够提供气泡尺度的流动信息与规律，对于建立实际流动条件下的本构关系具有重要的理论意义，是多相流模拟进一步发展的一个重要方向。本文即为采用 LBM 对多相流进行多尺度模拟方法的发展与探讨。 1. 格子玻尔兹曼方法格子玻尔兹曼方法（LBM）是近十几年来快速发展起来的一种非常有吸引力的计算方法，很多研究者已经将其应用到多个不同的领域，研究表明该方法具有很多独特的优点和广泛的适用范围（Luo, 1998; Chen & Doolen, 1998; Ladd et al. 2001; Succi, 2001）。LBM 是介于微观尺度和宏观尺度的新型模拟方法，该方法最近几年发展极为迅速，每年都有大量的相关 2

http://www.paper.edu.cn 研究文献出现，说明对 LBM 研究成为模拟领域热点课题。该方法基础理论介绍如下：非平衡统计力学中玻尔兹曼方程: f ∂ t ∂ ε + ∇ = f Q (1) Q 为碰撞项，进行 BGK 近似，即将碰撞看成对平衡状态的偏离，可得： f ∂ t ∂ ε + ∇ = − f 1 ( τ f − f eq ) (2) 将速度进行离散（以典型的 D2Q9 为例，有 9 个速度）： f ∂ α t ∂ 继续将速度在空间和时间上离散化： f t t , ( + α x δ t ) δ t δ x t , ) i x t , i f ( α f ( α x i + + − + + c t e δ δ α ε ∇ = − α f α 1 ( τ f α − f eq α ) (3) ) − f ( α x t , ) i = − 1 τ ⎡ ⎣ f ( α x t , ) i − f eq α ( x t , ) i ⎤ ⎦ (4) 化简整理可得： f ( α x i + e t δ δ α t t , + ) − f ( α x t , ) i = − 1 τ ⎡ ⎣ (5) 此即为 D2Q9 形式格子玻尔兹曼方程，其中 f 为离散的分配函数，其与宏观物理量之间 f ( α x t , ) i − f eq α ( x t i , ) , ⎤ ⎦ α = 0,1,2 8 K 的关系为： ρ = 8 =∑ f α α = 0 8 ∑ α = 0 f eq α u ρ = ， 8 ∑ α = 0 e f α α = 8 ∑ α = 0 e f eq α α (6) c = tδ δ x / ， c = ， 2 s c 2 3 p cρ= 2 s (7) 动力学粘度ν和松弛因子τ相关，即： = ⎛ ν τ −⎜ ⎝ 1 2 ⎞ ⎟ ⎠ sc t 2 δ ， τ = ν sc t 2 δ + (8) 1 2 九个方向上的速度集合为： e0＝（0，0）e1＝（1，0）e2＝（0，1）e3＝（-1，0）e4＝（0，-1） e5＝（1，1）e6＝（-1，1）e7＝（-1，-1）e8＝（1，-1）（9）以上简单阐述了 LBM 的基础，其中关于 BGK 近似，速度离散的模式，动力学粘度的推导都可由非平衡态统计力学详细给出（Succi, 2001）。 2.多相流基于 LBM 的多尺度模拟分析 LBM 将流体等效为具有一定速度分布的粒子集合。这些粒子位于格子的节点上并相互作用，其碰撞、传播和再分布形成流体复杂的宏观流动行为。这一特点使 LBM 能够方便地 3

http://www.paper.edu.cn 在模型中包含介观尺度的相互作用，成为介观模拟和跨尺度模拟的有效方法 (Glinski et al., 2001)，已经在多相流 (Sankaranarayanan et al., 2002)、多孔介质流动 (Wu et al., 2005)、微流体、悬浮体 (Ladd, 1994)、和非牛顿流体（Lallemand et al., 2003）以及复杂边界流动 (Kandhai et al., 1999) 等体系中得到了广泛应用。 Hazi et al. (2003) 等对基于 LBM 的气液多相流模型（气泡尺度）进行了总结，典型的模型包括颜色模型 (Color model) ，拟势能模型 (Pseudo potential model: Shan & Chen, 1993) 以及自由能模型 (Free energy model) 。这些模型能够对气液体系中的气泡行为进行模拟，但一般还限于气液两相密度之比较相对较小 (<10) 的情形。 Ladd (1994) 最初成功地将 LBM 用于液固悬浮体系（颗粒尺度）的模拟研究，随后不少研究者相继在这一领域开展工作 (Wylie et al., 2003)，表明该方法鲁棒性好、效率高，适用于颗粒数很大的颗粒流动体系。文献中现有的报道大多针对该方法在模拟液固悬浮体系时颗粒-流体边界条件的处理、颗粒受力的计算方法以及颗粒的运动行为，对颗粒受力引起的液固体系流变行为的研究则非常有限。近年来，一些学者在多尺度方法用于多相流研究方面开展了重要的工作 (Li & Kwauk, 2003; van der Hoef et al., 2004) ，但是如何将多尺度的方法在模拟中具体实现还处于探索阶段。van der Hoef 等 (2004) 对多尺度方法在多相流模拟中的实现进行了探索，分别采用双流体模型和格子 Boltzmann 模型对宏观尺度行为和颗粒尺度行为进行模拟；在双流体模型中，相间作用项采用颗粒尺度模拟的结果进行封闭。在该工作中，对不同尺度的模拟基于不同的理论框架，不能建立起统一的模拟平台。本文基于浆态体系数值模拟和 LBM 两方面的研究进展，从宏观尺度模拟，以及颗粒受力行为和气泡动力学模拟等几方面出发，在 LBM 的框架内同时实现对浆态体系介观尺度和宏观尺度的统一模拟，有利于深入地揭示其流动机理。 3.多相流基于 LBM 的多尺度模拟方法 3.1 基于 LBM 的双流体模型我们研究室提出了基于 LBM 的宏观尺度双流体模型，基于 LBM 的双流体模型的最终形式为（Wang et al., 2005）： f ( , α x i k + t e δ δ α t t , + ) − f k ( , α x t , ) i = 1 τ k ⎡ ⎣ f ( , α x t , ) i k − ) f eq ( k i , ( x t , ) i ⎤ ⎦ + ∇ p T x ( ε k ) + F k , α (10) 其中 f 含义与(5)式中的相同。ε 代表相含率，k 代表相，F 代表相间作用力。如果相间作用力用传统方法描述，基于此模型可对多相流宏观流动行为进行模拟。式 (10) 中相间作用力项的处理需要进行进一步讨论，在这里相间作用力（曳力，升力等）可以用一些成熟的基于 LBM 的气泡（颗粒）介观尺度模型计算得到，接着将介观尺度的信息传递到宏观尺度， 4

http://www.paper.edu.cn 同时两个尺度都是基于 LBM 进行模拟，从而可以形成统一的模拟平台。以下分别对本文采用的基于 LBM 的气泡动力学模型和颗粒动力学模型做简单介绍。 3.2 基于 LBM 气泡动力学模型本文采用拟势能模型 (Pseudo potential model: Shan & Chen, 1993)进行气泡动力学行为模拟，其中单气泡形成过程和气泡在流场中变形结果如图 1，2 所示。该模型主要假设两相之间有一拟势存在，利用该模型可以准确计算出气泡在流场作用下所受升力，曳力，虚拟质量力等，文献（Sankaranarayanan & Sundaresan, 2002）中对此进行了详细研究。. 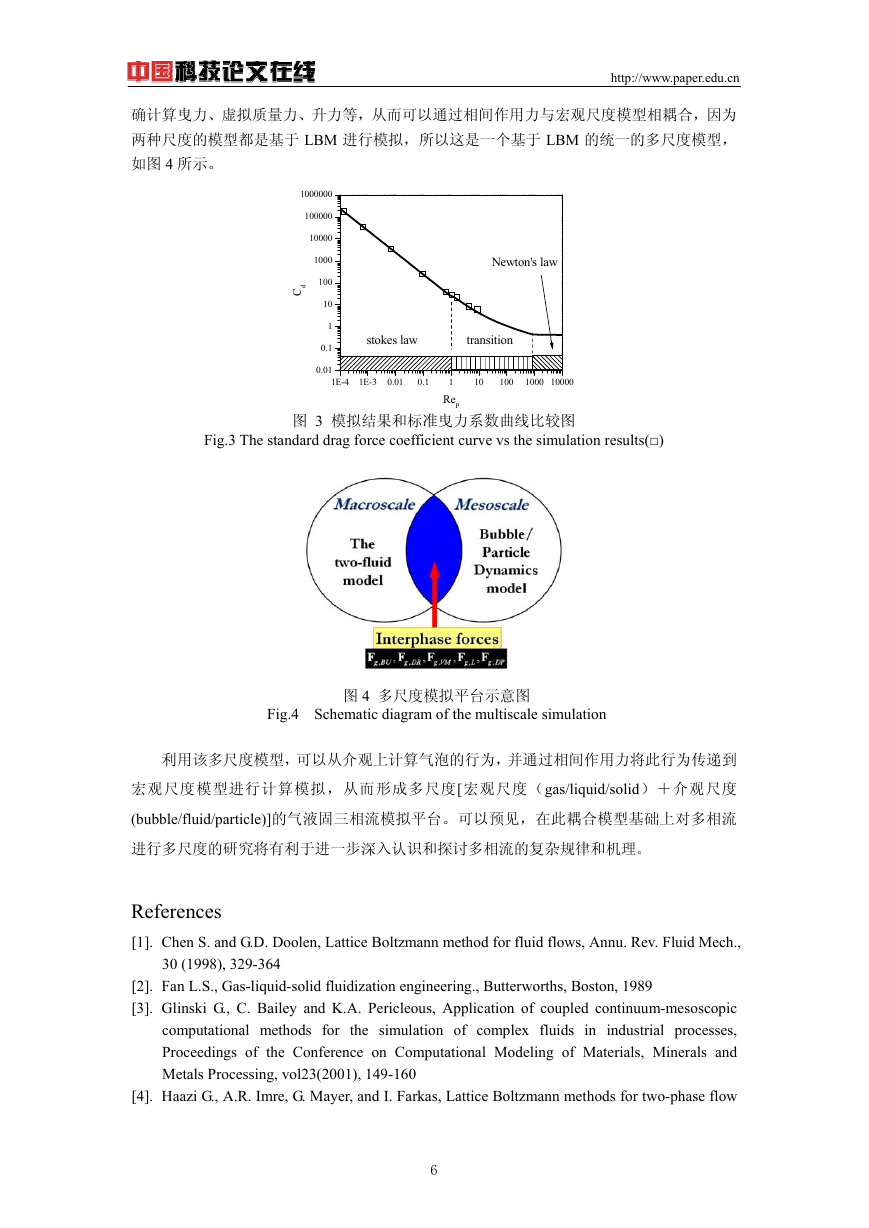图 1 用拟势能模型计算单气泡形成过程示意图 Fig.1 The formation process of a bubble(drop) by the pseudo potential model 图 2 气泡在流场中变形模拟结果 Fig.2 The simulation results of bubble deformation 3.3 基于 LBM 颗粒动力学模型本文主要采用（Ladd, 1994）的方法进行颗粒动力学模拟。利用该模型可以准确计算出颗粒在流场中所受曳力，升力等（Liu et al, 2007b），从而可以准确描述颗粒运动行为。该模型和传统颗粒受力描述定量吻合很好，如图 3 所示。由以上分析可知，多相浆态体系介观尺度和宏观尺度的模拟均可采用 LBM，从而将不同尺度的模拟纳入到相同的理论框架内，建立统一的多尺度模拟平台，这对深入认识多相流动机制，推进多尺度方法的具体应用具有重要意义。 4 结论本文基于 LBM 建立了宏观尺度的双流体模型，并耦合在气泡（颗粒）尺度（介观尺度）上适于计算相间相互作用力的气泡（颗粒）动力学模型，该气泡（颗粒）动力学模型可以准 5

确计算曳力、虚拟质量力、升力等，从而可以通过相间作用力与宏观尺度模型相耦合，因为两种尺度的模型都是基于 LBM 进行模拟，所以这是一个基于 LBM 的统一的多尺度模型，如图 4 所示。 http://www.paper.edu.cn 1000000 100000 10000 d C 1000 100 10 1 0.1 Newton's law stokes law transition 0.01 1E-4 1E-3 0.01 0.1 10 100 1000 10000 1 ReP 图 3 模拟结果和标准曳力系数曲线比较图 Fig.3 The standard drag force coefficient curve vs the simulation results(□) 图 4 多尺度模拟平台示意图 Fig.4 Schematic diagram of the multiscale simulation 利用该多尺度模型，可以从介观上计算气泡的行为，并通过相间作用力将此行为传递到宏观尺度模型进行计算模拟，从而形成多尺度[宏观尺度（gas/liquid/solid）＋介观尺度 (bubble/fluid/particle)]的气液固三相流模拟平台。可以预见，在此耦合模型基础上对多相流进行多尺度的研究将有利于进一步深入认识和探讨多相流的复杂规律和机理。 References [1]. Chen S. and G.D. Doolen, Lattice Boltzmann method for fluid flows, Annu. Rev. Fluid Mech., 30 (1998), 329-364 [2]. Fan L.S., Gas-liquid-solid fluidization engineering., Butterworths, Boston, 1989 [3]. Glinski G., C. Bailey and K.A. Pericleous, Application of coupled continuum-mesoscopic computational methods for the simulation of complex fluids in industrial processes, Proceedings of the Conference on Computational Modeling of Materials, Minerals and Metals Processing, vol23(2001), 149-160 [4]. Haazi G., A.R. Imre, G. Mayer, and I. Farkas, Lattice Boltzmann methods for two-phase flow 6

http://www.paper.edu.cn modeling, Ann. Nucl. Energy, 29(2002), 1421-1453 [5]. Inamuro T., T. Ogata, S. Tajima and N. Konishi, A lattice Boltzmann method for incompressible two-phase flows with large density differences, J. Comp. Phys., 198 (2004) 628-644 [6]. Kandhai D., D.J.E.Vidal, A.G. Hoekstra, H. Hoefsloot, P. Iedema, P.M.A. Sloot, Lattice-Boltzmann and finite element simulations of fluid flow in a SMRX static mixer reactor, Int. J. Num. Meth. in Fluids, 31(1999)6, 1019-1033 [7]. Ladd A.J.C. and R.Verberg, Lattice-Boltzmann simulations of particle-fluid suspensions, J. Stat. Phys., 104(2001), 1191-1251 [8]. Ladd A.J.C., Numerical simulations of particulate suspensions via discretized Boltzmann equation. Part 1. Theoretical foundation; Part 2. Numerical results, J. Fluid Mech., 271(1994), 285-339. [9]. Lallemand P., D. d'Hmieeres, L.S. Luo, and R. Rubinstein, Theory of the lattice Boltzmann method: Three-dimensional model for linear viscoelastic fluids, Phys. Rev. E, 67(2003), 021203. [10]. Li J.H., M. Kwauk, Exploring complex systems in chemical engineering - the multi- scale methodology, Chemical Engineering Science, 58(2003), 521-535. [11]. Li Y., J.P. Zhang and L.S. Fan, Numerical simulation of gas-liquid-solid fluidization systems using a combined CFD-VOF-DPM method: bubble wake behavior, Chemical Engineering Science, 54 (1999), 5101-5107 [12]. Liu M.L., Wang T.F., Wang J.F., A lattice-Boltzmann simulation study of the drag and lift behavior of particles, Proceedings of The 3rd Asian Particle Technology Symposium 2007b,Beijing [13]. Liu M.L., Wang T.F., Yu W., Wang J.F., Hydrodynamics of a Slurry Airlift Reactor in High Solid Concentrations, Chemical Engineering Science, 2007a, In press. [14]. Luo L.S., Unified Theory of the lattice Boltzmann models for nonideal gases, Phys. Rev. Lett., 81(1998), 1618-1621; [15]. Sankaranarayanan K. and S. Sundaresan, Lift force in bubbly suspensions, Chemical Engineering Science, 57(2002), 3521-3542. [16]. Shan X. and H. Chen, Lattice Boltzmann model for simulating flows with multiple phases and components, Phys. Rev. E., 47(1993), 1815; [17]. Succi S., The Lattice Boltzmann Equation for Fluid Dynamics and Beyond, Clarendon Press, Oxford, 2001. [18]. van der Hoef M.A., M. van Sint Annaland, J.A.M. Kuipers, Computational fluid dynamics for dense gas–solid fluidized beds: a multi-scale modeling strategy, Chemical Engineering Science, 59(2004), 5157-5165 [19]. Wang T. F., J. F. Wang, Two-Fluid Model Based on the Lattice Boltzmann Equation, Phys. Rev. E, 71(2005), 045301(R). [20]. Wu H.R., Y.L. He, G.H. Tang, W.Q. Tao, Lattice Boltzmann simulation of flow in porous media on non-uniform grids, Prog. Comp. Fluid Dyn., 5(2005), 97-103 [21]. Wylie J.J., D.L. Koch and A.J.C. Ladd, Rheology of suspensions with high particle inertia and moderate fluid inertia, J. Fluid Mech., 480(2003), 95-118 7

分享到：

赞收藏

资料库

一种基于LBM的气液固三相流多尺度模拟方法 .pdf

相关推荐

开发技术

热门标签

最新资料