logo资料库

bellman-ford算法及例题讲解.ppt

发布时间：2022-06-12 发布人：admin 分类：说明书 资料大小：1.15M 资料格式：ppt 举报 版权申诉
第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
资料共11页，剩余部分请下载后查看
    HAERBIN ENGINEERING UNIVERSITY 现代通信网络基础 Bellman-Ford 算法 哈尔滨工程大学 通信六班 2017 1
    HAERBIN ENGINEERING UNIVERSITY Bellman-Ford 算法 贝尔曼-福特算法（Bellman-Ford）是由 Richard Bellman 和 Lester Ford 创立的，求解 单源最短路径问题 的一种算法。有时候这种 算法也被称为 Moore-BellmanFord 算法，因 Edward F. Moore 也为这个算法的发展做出了 贡献。为了能够求解边上带有负权值的单源最 短路径问题，Bellman(贝尔曼)和Ford(福特)提 出了从源点逐次途经其他顶点，以缩短到达终 点的最短路径长度的方法。 2
    HAERBIN ENGINEERING UNIVERSITY Bellman-Ford 算法 基本内容： – 从给定的源结点找出一条最短路径，该最短路 径是从所有最多只含有一条链路的路径中选择出 来的 – 接着再找出条件为所有路径最多只含两条链路 的最短路径，依此类推 3
    HAERBIN ENGINEERING UNIVERSITY Bellman-Ford 算法 Bellman-Ford 算法可以用公式来表示 首先做以下定义: –s= 源结点 –w(i,j)= 结点i 到结点j 之间的链路代价。 w(i,i)=0；两个结点不直接连接时，w(i,j)=∞； –h= 在算法目前阶段中的路径具有的最大链路数 –Lh(n)= 在不多于h 条链路的条件下，从结点s 到结 点n 的最小代价路径的代价 4
    HAERBIN ENGINEERING UNIVERSITY Bellman-Ford 算法 Step 1. 初始化 – L0(n) = ∞, 对所有n ≠ s – Lh(s) = 0, 对所有h Step 2. 更新 对每个后继的h ≥ 0 –对每个n ≠ s, 计算: Lh+1(n)=minj[Lh(j)+w(j,n)] –将n 与前一次处理的结点j 相连接，以获取最小值， 并删除在以前循环时形成n 与任何前次处理结点之间的 链接。从s 到n 的路径以从j 到n 的路径结束 5
    HAERBIN ENGINEERING UNIVERSITY Bellman-Ford 算法 Step 3.重复 –不断地重复第2步，当h=K时，并且对于每个 目的结点n，算法将从s到n的长度为K+1的可能 路径与前一次循环结束时得到的路径相比较。 如果前次更短的路径具有较小的代价，那么将 仍然保持前次的路径，否则s和n之间定义一条 长度为K+1的新路径。 –这条路径含有长度为K的从s到某个结点j的路 径，再加上从结点j到结点n的直接一跳 6
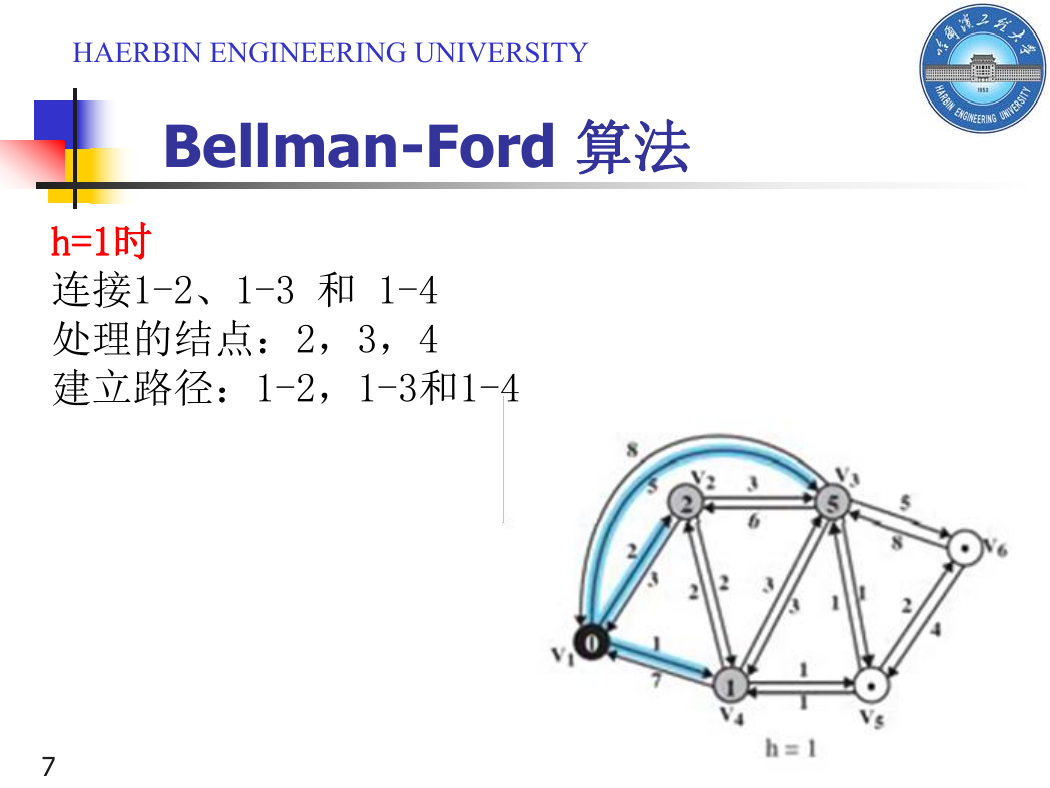
    HAERBIN ENGINEERING UNIVERSITY Bellman-Ford 算法 h=1时 连接1-2、1-3 和 1-4 处理的结点：2，3，4 建立路径：1-2，1-3和1-4 7
    HAERBIN ENGINEERING UNIVERSITY Bellman-Ford 算法 h=2时 连接1-3-2和1-4-2，1-2-3和1-4-3，1-2-4和1-3-4 1- 3-5和1-4-5，以及1-3-6 考察结点1到结点2，3，4，5，6的最小代价路径 本次处理的结点：3，5，6 修改/建立路径1-4-3，1-4-5和1-3-6 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料