logo资料库

变异函数及其计算理论.pdf

发布时间：2022-06-03 发布人：admin 分类：说明书 资料大小：1.74M 资料格式：pdf 举报 版权申诉
第1页 / 共18页
第2页 / 共18页
第3页 / 共18页
第4页 / 共18页
第5页 / 共18页
第6页 / 共18页
第7页 / 共18页
第8页 / 共18页
资料共18页，剩余部分请下载后查看
    变异函数教程 Variogram Tutorial Randal Barnes Golden Software, Inc. 变异函数教程 作者：Randal Barnes(兰德尔·巴恩斯) Golden Software 软件公司 翻译：程贤辅 2012.12.24 目录 1 - 引言 2 - 什么是一个变异函数，它代表什么呢？ 3 - 什么是变异函数？ 4 - 变异函数网格 5 - 建模全方位的变异函数 6 - 变异函数模型各向异性 7 - 经验法则 8 - 常见问题 9 - 一些地质统计学的参考文献 1 引言 变异函数刻划了数据集在空间上的连续性或粗糙程度。普通一维的两个数据集的统计数据几乎相 同，但在空间上的连续性可能是完全不同的。其理由请参阅第2节变异函数的部分内容。 变异函数的分析包括从数据计算出来的实验变异函数和变异函数模型拟合出来的数据。实验变异 函数的计算方法是有关Z值的均方差的一半，该Z超过指定的分隔距离和方向观测到的所有数据对。 它被绘制为一个二维图。用于计算实验变异函数的数学公式的详细信息，请参阅第3节。 该变异函数模型是选自一组描述空间关系的数学函数。相应的模型是选自与实验变差函数的曲线 形状相匹配的数学函数的形状曲线。 请参阅网上Surfer用户指南和Surfer帮助中有关每个函数 的曲线形状图中的变异函数模型图形主题。要交代的几何异向 性（在不同方向上的可变空间连续性），单独的实验和模型变 异函数可以计算数据集中的不同的方向。 2 什么是一个变异函数所代表的？ ~ 1 ~
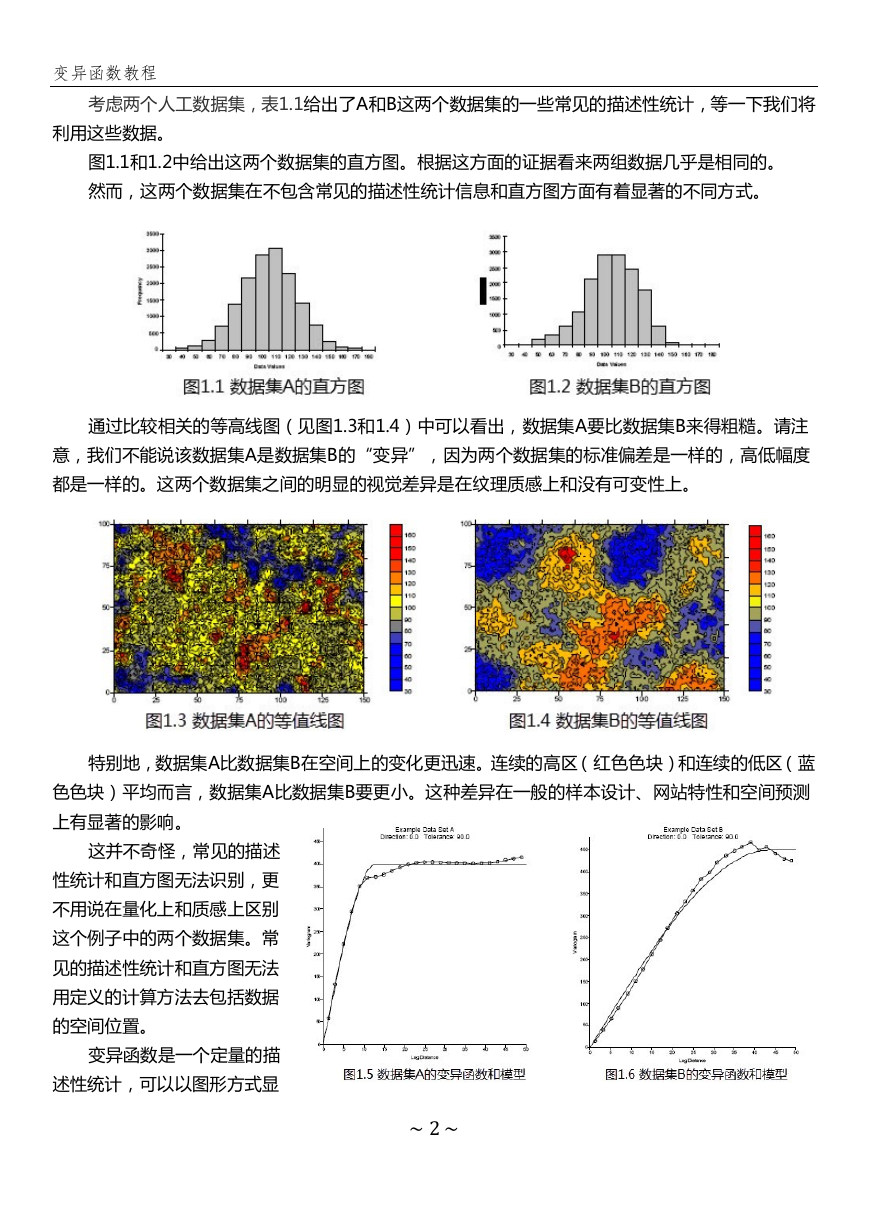
    变异函数教程 考虑两个人工数据集，表1.1给出了A和B这两个数据集的一些常见的描述性统计，等一下我们将 利用这些数据。 图1.1和1.2中给出这两个数据集的直方图。根据这方面的证据看来两组数据几乎是相同的。 然而，这两个数据集在不包含常见的描述性统计信息和直方图方面有着显著的不同方式。 通过比较相关的等高线图（见图1.3和1.4）中可以看出，数据集A要比数据集B来得粗糙。请注 意，我们不能说该数据集A是数据集B的“变异”，因为两个数据集的标准偏差是一样的，高低幅度 都是一样的。这两个数据集之间的明显的视觉差异是在纹理质感上和没有可变性上。 特别地，数据集A比数据集B在空间上的变化更迅速。连续的高区（红色色块）和连续的低区（蓝 色色块）平均而言，数据集A比数据集B要更小。这种差异在一般的样本设计、网站特性和空间预测 上有显著的影响。 这并不奇怪，常见的描述 性统计和直方图无法识别，更 不用说在量化上和质感上区别 这个例子中的两个数据集。常 见的描述性统计和直方图无法 用定义的计算方法去包括数据 的空间位置。 变异函数是一个定量的描 述性统计，可以以图形方式显 ~ 2 ~
    变异函数教程 示在数据集空间特征上的连续性（即粗糙度）的方式。图1.5和1.6所示为这两个数据集的变异函数图。 两组曲线在初始斜率上的差异是明显的。 3 变异函数是什么？ 变差函数的数学定义是这样的： (3.1) 其中，Z(x,y)是相关变量在点(x,y)的有效值，而ε[]为统计期望因子。请注意，变异函数，( ) 函 数是其中的点与点之间的距离(Δx,Δy)的函数，而不是特定位置(x,y)的函数。这个数学定义是一个有用的 抽象概括，但又不是那么容易应用到观测值的分析上。 我们现在考虑观测到的n组数据：{(X1,Y1,Z1),(X2,Y2,Z2),……(Xn,Yn,Zn)}，其中点(Xi,Yi)为观测点 i 的位置，而 Zi 则是与该观测点相关的观测值。对于 n(n-1)/2 的位置，我们有(前后)唯一的观测值 对，在每一个这样的数据对中，我们可以计算出相关联的间隔矢量： 当我们要推导出某特定间隔矢量的变异函数(Δx,Δy)时，我们将使用所有的间隔矢量的数据对， (Δxi,j, Δyi,j) = (xi-xj, yi-yj) (3.2) 它是近似等于这种间隔的有效值： 让 S(Δx,Δy)代表所有数据对的集合： (Δxi,j, Δyi,j) ≈ (Δx,Δy) S(Δx,Δy)= { (i,j) | (Δxi,j, Δyi,j) ≈ (Δx,Δy) } (3.3) (3.4) 此外，我们让N(Δx,Δy)等于S(Δx,Δy)的数据对的数目。从观测数据来推断变异函数，然后，我们 将采用实验变异函数的公式。 (3.5) Δ Δ 即，有效值的特定间隔矢量的实验变异函 数，是该矢量的增量的观测间隔的所有数据对 的Z值的差的平方的平均值的一半。(很拗口 的句子，参看上面的公式才好理解——译者)。 4 变异函数网格 如 果 有 n 个 观 测 数 据 ， 那 么 就 有 n(n-1)/2 个唯一的观测对。因此，即使是一 个中等尺度的数据集也会产生大量的数据对。 例如，如果 n=500，那么就有 n(n-1)/2 = 124745 个数据对(应该是124750个数据对— —译者)。即使对于一个快速的计算机，对这样大量的数据对进行操作也是非常耗时的。Surfer将预 ~ 3 ~
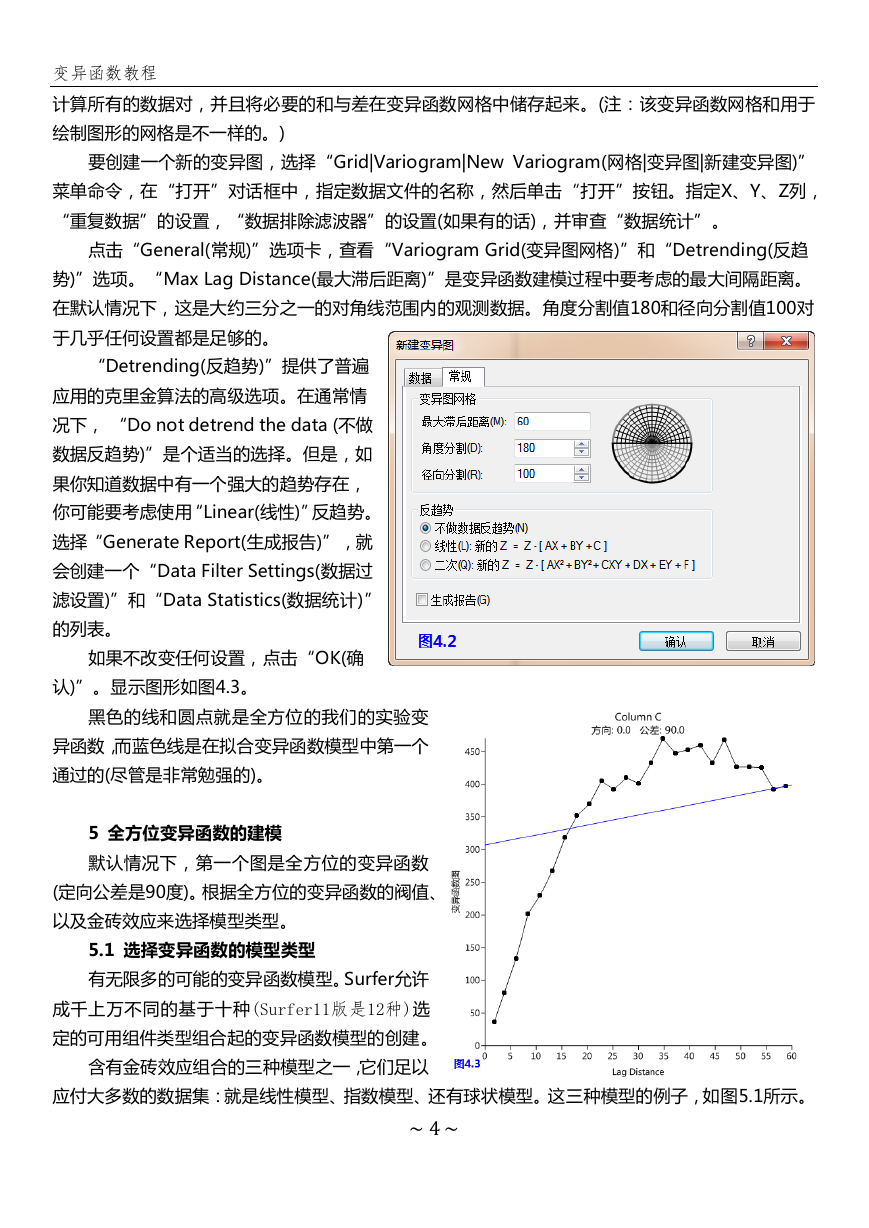
    变异函数教程 计算所有的数据对，并且将必要的和与差在变异函数网格中储存起来。(注：该变异函数网格和用于 绘制图形的网格是不一样的。) 要创建一个新的变异图，选择“Grid|Variogram|New Variogram(网格|变异图|新建变异图)” 菜单命令，在“打开”对话框中，指定数据文件的名称，然后单击“打开”按钮。指定X、Y、Z列， “重复数据”的设置，“数据排除滤波器”的设置(如果有的话)，并审查“数据统计”。 点击“General(常规)”选项卡，查看“Variogram Grid(变异图网格)”和“Detrending(反趋 势)”选项。“Max Lag Distance(最大滞后距离)”是变异函数建模过程中要考虑的最大间隔距离。 在默认情况下，这是大约三分之一的对角线范围内的观测数据。角度分割值180和径向分割值100对 于几乎任何设置都是足够的。 “Detrending(反趋势)”提供了普遍 应用的克里金算法的高级选项。在通常情 况下， “Do not detrend the data (不做 数据反趋势)”是个适当的选择。但是，如 果你知道数据中有一个强大的趋势存在， 你可能要考虑使用“Linear(线性)”反趋势。 选择“Generate Report(生成报告)”，就 会创建一个“Data Filter Settings(数据过 滤设置)”和“Data Statistics(数据统计)” 的列表。 如果不改变任何设置，点击“OK(确 认)”。显示图形如图4.3。 黑色的线和圆点就是全方位的我们的实验变 异函数，而蓝色线是在拟合变异函数模型中第一个 通过的(尽管是非常勉强的)。 5 全方位变异函数的建模 默认情况下，第一个图是全方位的变异函数 (定向公差是90度)。根据全方位的变异函数的阀值、 以及金砖效应来选择模型类型。 5.1 选择变异函数的模型类型 有无限多的可能的变异函数模型。Surfer允许 成千上万不同的基于十种(Surfer11版是12种)选 定的可用组件类型组合起的变异函数模型的创建。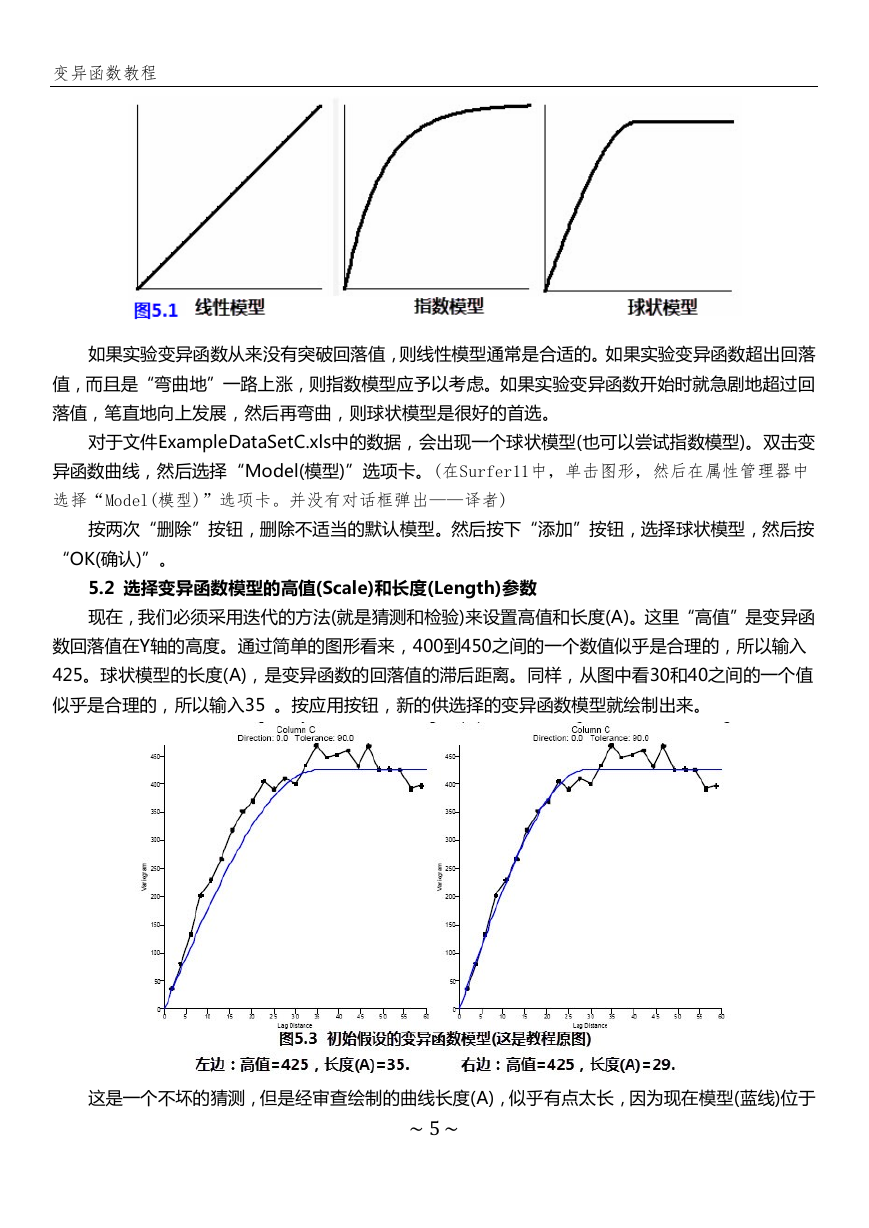 含有金砖效应组合的三种模型之一，它们足以 应付大多数的数据集：就是线性模型、指数模型、还有球状模型。这三种模型的例子，如图5.1所示。 ~ 4 ~
    变异函数教程 如果实验变异函数从来没有突破回落值，则线性模型通常是合适的。如果实验变异函数超出回落 值，而且是“弯曲地”一路上涨，则指数模型应予以考虑。如果实验变异函数开始时就急剧地超过回 落值，笔直地向上发展，然后再弯曲，则球状模型是很好的首选。 对于文件ExampleDataSetC.xls中的数据，会出现一个球状模型(也可以尝试指数模型)。双击变 异函数曲线，然后选择“Model(模型)”选项卡。(在Surfer11中，单击图形，然后在属性管理器中 选择“Model(模型)”选项卡。并没有对话框弹出——译者) 按两次“删除”按钮，删除不适当的默认模型。然后按下“添加”按钮，选择球状模型，然后按 “OK(确认)”。 5.2 选择变异函数模型的高值(Scale)和长度(Length)参数 现在，我们必须采用迭代的方法(就是猜测和检验)来设置高值和长度(A)。这里“高值”是变异函 数回落值在Y轴的高度。通过简单的图形看来，400到450之间的一个数值似乎是合理的，所以输入 425。球状模型的长度(A)，是变异函数的回落值的滞后距离。同样，从图中看30和40之间的一个值 似乎是合理的，所以输入35 。按应用按钮，新的供选择的变异函数模型就绘制出来。 这是一个不坏的猜测，但是经审查绘制的曲线长度(A)，似乎有点太长，因为现在模型(蓝线)位于 ~ 5 ~
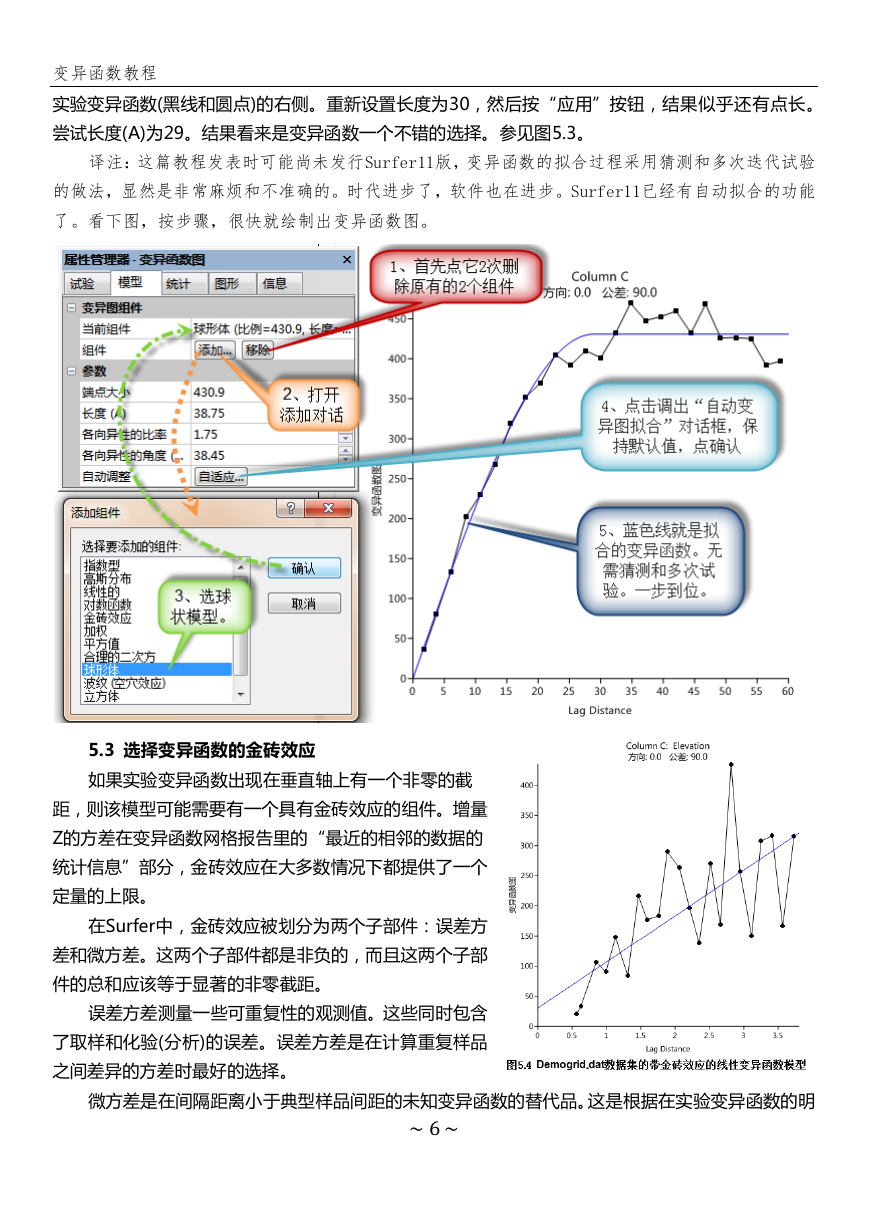
    变异函数教程 实验变异函数(黑线和圆点)的右侧。重新设置长度为30，然后按“应用”按钮，结果似乎还有点长。 尝试长度(A)为29。结果看来是变异函数一个不错的选择。参见图5.3。 译注：这篇教程发表时可能尚未发行Surfer11版，变异函数的拟合过程采用猜测和多次迭代试验 的做法，显然是非常麻烦和不准确的。时代进步了，软件也在进步。Surfer11已经有自动拟合的功能 了。看下图，按步骤，很快就绘制出变异函数图。 5.3 选择变异函数的金砖效应 如果实验变异函数出现在垂直轴上有一个非零的截 距，则该模型可能需要有一个具有金砖效应的组件。增量 Z的方差在变异函数网格报告里的“最近的相邻的数据的 统计信息”部分，金砖效应在大多数情况下都提供了一个 定量的上限。 在Surfer中，金砖效应被划分为两个子部件：误差方 差和微方差。这两个子部件都是非负的，而且这两个子部 件的总和应该等于显著的非零截距。 误差方差测量一些可重复性的观测值。这些同时包含 了取样和化验(分析)的误差。误差方差是在计算重复样品 之间差异的方差时最好的选择。 微方差是在间隔距离小于典型样品间距的未知变异函数的替代品。这是根据在实验变异函数的明 ~ 6 ~
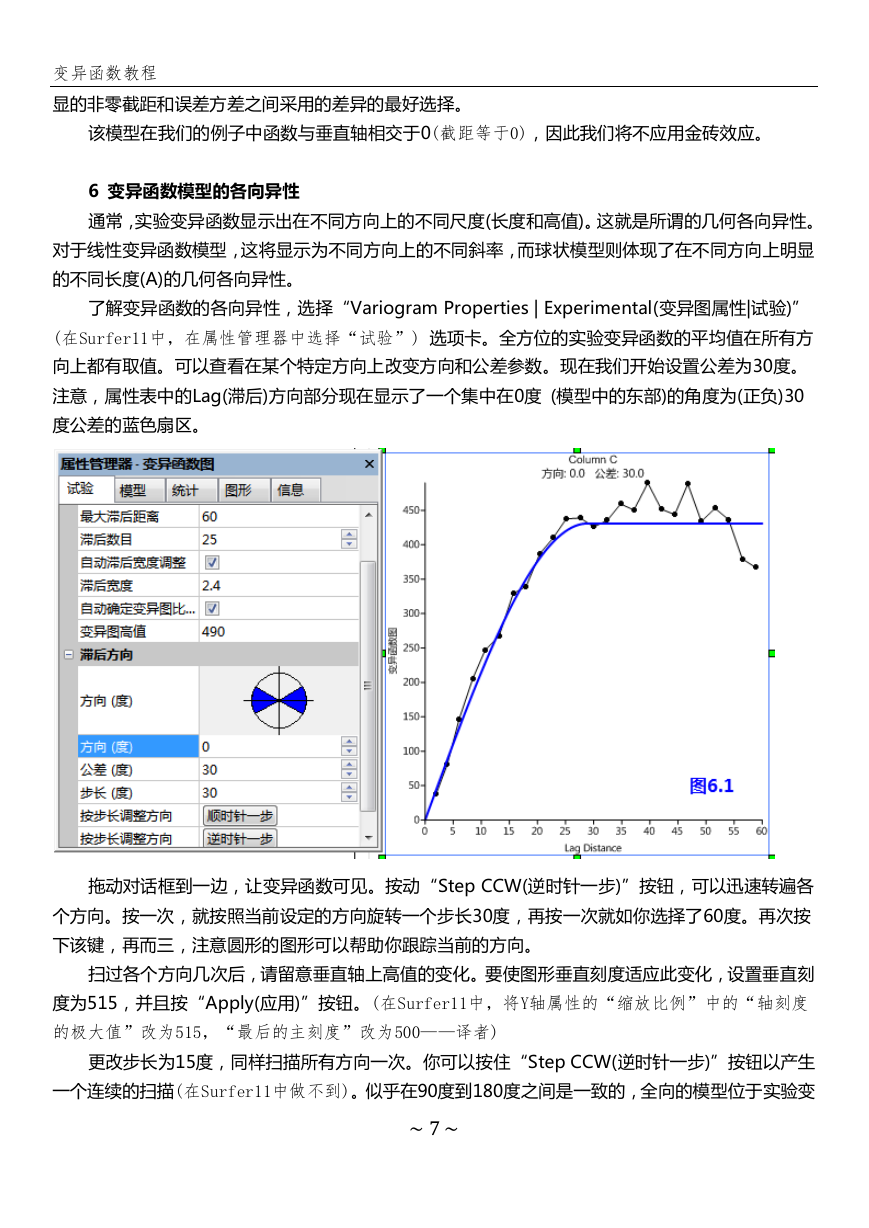
    变异函数教程 显的非零截距和误差方差之间采用的差异的最好选择。 该模型在我们的例子中函数与垂直轴相交于0(截距等于0)，因此我们将不应用金砖效应。 6 变异函数模型的各向异性 通常，实验变异函数显示出在不同方向上的不同尺度(长度和高值)。这就是所谓的几何各向异性。 对于线性变异函数模型，这将显示为不同方向上的不同斜率，而球状模型则体现了在不同方向上明显 的不同长度(A)的几何各向异性。 了解变异函数的各向异性，选择“Variogram Properties | Experimental(变异图属性|试验)” (在Surfer11中，在属性管理器中选择“试验”) 选项卡。全方位的实验变异函数的平均值在所有方 向上都有取值。可以查看在某个特定方向上改变方向和公差参数。现在我们开始设置公差为30度。 注意，属性表中的Lag(滞后)方向部分现在显示了一个集中在0度 (模型中的东部)的角度为(正负)30 度公差的蓝色扇区。 拖动对话框到一边，让变异函数可见。按动“Step CCW(逆时针一步)”按钮，可以迅速转遍各 个方向。按一次，就按照当前设定的方向旋转一个步长30度，再按一次就如你选择了60度。再次按 下该键，再而三，注意圆形的图形可以帮助你跟踪当前的方向。 扫过各个方向几次后，请留意垂直轴上高值的变化。要使图形垂直刻度适应此变化，设置垂直刻 度为515，并且按“Apply(应用)”按钮。(在Surfer11中，将Y轴属性的“缩放比例”中的“轴刻度 的极大值”改为515，“最后的主刻度”改为500——译者) 更改步长为15度，同样扫描所有方向一次。你可以按住“Step CCW(逆时针一步)”按钮以产生 一个连续的扫描(在Surfer11中做不到)。似乎在90度到180度之间是一致的，全向的模型位于实验变 ~ 7 ~
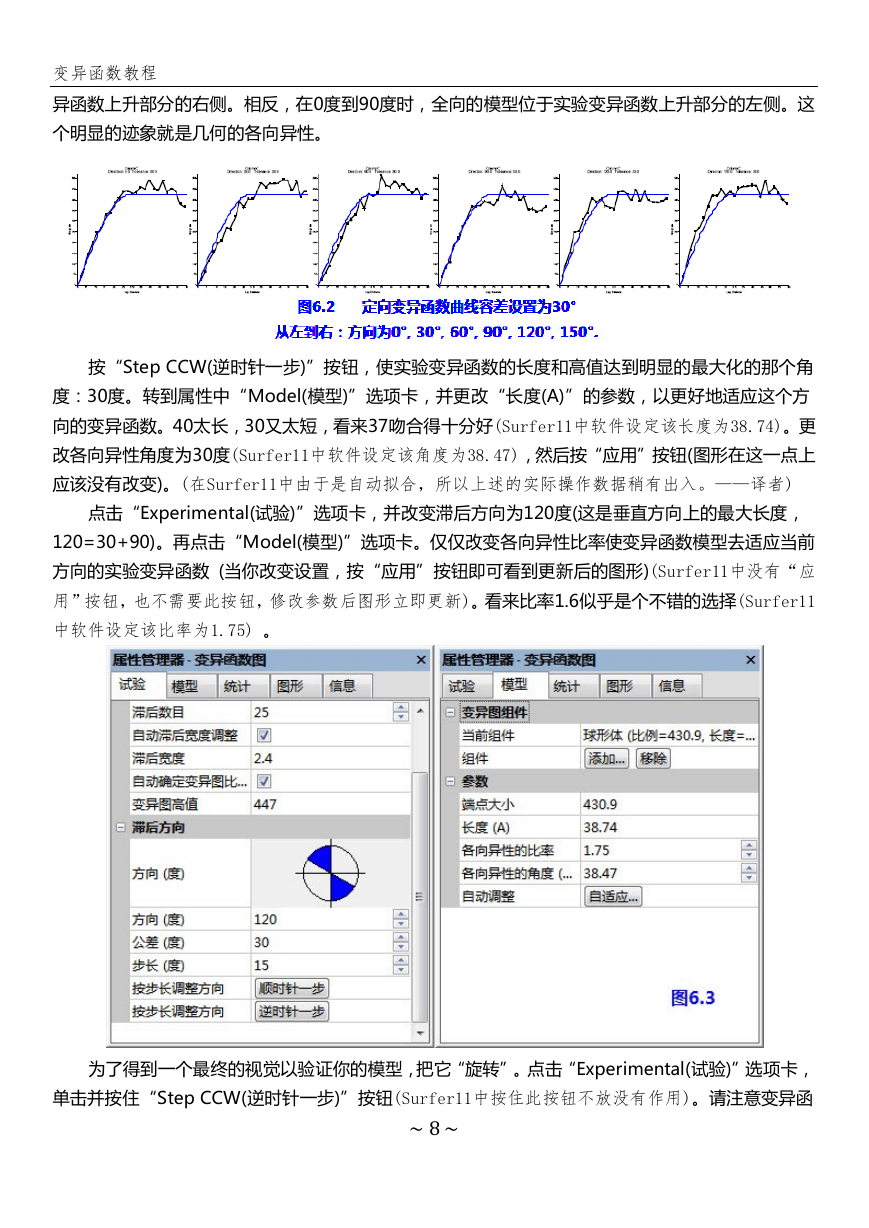
    变异函数教程 异函数上升部分的右侧。相反，在0度到90度时，全向的模型位于实验变异函数上升部分的左侧。这 个明显的迹象就是几何的各向异性。 按“Step CCW(逆时针一步)”按钮，使实验变异函数的长度和高值达到明显的最大化的那个角 度：30度。转到属性中“Model(模型)”选项卡，并更改“长度(A)”的参数，以更好地适应这个方 向的变异函数。40太长，30又太短，看来37吻合得十分好(Surfer11中软件设定该长度为38.74)。更 改各向异性角度为30度(Surfer11中软件设定该角度为38.47)，然后按“应用”按钮(图形在这一点上 应该没有改变)。(在Surfer11中由于是自动拟合，所以上述的实际操作数据稍有出入。——译者) 点击“Experimental(试验)”选项卡，并改变滞后方向为120度(这是垂直方向上的最大长度， 120=30+90)。再点击“Model(模型)”选项卡。仅仅改变各向异性比率使变异函数模型去适应当前 方向的实验变异函数 (当你改变设置，按“应用”按钮即可看到更新后的图形)(Surfer11中没有“应 用”按钮，也不需要此按钮，修改参数后图形立即更新)。看来比率1.6似乎是个不错的选择(Surfer11 中软件设定该比率为1.75) 。 为了得到一个最终的视觉以验证你的模型，把它“旋转”。点击“Experimental(试验)”选项卡， 单击并按住“Step CCW(逆时针一步)”按钮(Surfer11中按住此按钮不放没有作用)。请注意变异函 ~ 8 ~
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料