logo资料库

大规模MIMO.docx

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：0.85M 资料格式：docx 举报 版权申诉
第1页 / 共18页
第2页 / 共18页
第3页 / 共18页
第4页 / 共18页
第5页 / 共18页
第6页 / 共18页
第7页 / 共18页
第8页 / 共18页
资料共18页，剩余部分请下载后查看
    大规模 MIMO 系统综述 姚翠翠 摘要： MIMO(multiple-input multiple-output)技术日益成熟，但传统的 MIMO 技术并不能满足当代呈指数上涨的无线数据需求。。目前移动用 户的爆炸式增长，频率资源紧缺、能源的巨大消耗以及网络的优化问 题都不容忽视。当前移动通信的后续发展面临着两个关键问题，一是 在小范围、多用户下如何保证大容量的数据传输，二是高数据流量导 致资费大大提升，影响着用户对于高速网络的使用，如何降低网络成 本。而这些问题都需要通过新技术来解决。世界各国在推动第四代移 动通信产业化工作的同时，已开始着眼于新一代无线移动通信技术 （5G）的研究，力求使无线移动通信系统性能和产业规模产生新的飞 跃。在 2010 年底，贝尔实验室科学家 Thomas L.Marzetta 提出了大 规模 MIMO(Large Scale MIMO),也叫 Massive MIMO 的概念。 关键字：大规模 MIMO,和速率，信道估计，下行预编码，上行检测 1.引言 与传统多输入多输出 MIMO 系统相比,大规模 MIMO 系统通过在基站端 配备大量低功率天线,可以有效地提升频谱效率,提高链路可靠性,降 低能量损耗。对于大规模 MIMO 系统,目前仍有许多技术问题亟待研究, 比如理论方面的容量限值分析、信道估计、功率分配策略等,实际设 计方面的导频设计、低功率传输设计等。本论文首先分析了大规模 MIMO 系统的和速率上界,然后对信道估计、下行预编码和上行检测等
    关键技术进行了深入研究。最后,在信道建模,用户调度等方面进行了 展望,为大规模 MIMO 的发展提供了思路 爆发性的无线数据服务的发展需要更多新的频谱资源，而能被未来无 线通信系统利用的是昂贵而有限的。我们知道，在使用多个发射/接 收天线的 MIMO 系统通过空间复用和其多样性可保证高容量和链路可 靠性。MIMO 技术日趋成熟，它结合正交频分复用技术或是正交频分 复用和正交码分复用技术已应用到 4G 和超出 4G 的系统。因为 MIMO 系统容量随着收发机在丰富散射环境下的最小天线数而快速增加，图 1 所示的大规 模 MIMO 系统通过使用空间复用和减轻干扰的大规模 MIMO 系统是解决 无线数据服务指数增长问题的最重要的技术之一。就功效而言，大规 模的 MIMO 系统利用信道状态信息，同时给特定的用户选择性的传输 集中地光束信号，以提高信噪比和减少任意天线发送大量给定信息所 需的功率。大规模的 MIMO 系统可以准确的解决最佳点的问题，最佳 点就是需要传送的数据是增加的，然而传输需要的能量是下降的点。 因此传输需要的总能量会明显的减少。这是一个很好的特性，因此在 无线通信中节能变得越来越重要。由于低能耗和高频谱效率，大规模
    的 MIMO 系统会产生很好的经济效益。 大规模的 MIMO 不仅可以提供容量的剧增，同时还能显著地节能， 但它在网络提供方式上要有很大的改变，因为安装大量的额外天线会 引起一些特定的问题。首先，随机事件（如信道特性）趋于确定性的 事件，通过使用大量传输/接收天线，高维矩阵的空间变大，但随着 天线阵列的增大，它渐渐受到制约。其次，天线阵列的孔径越大，天 线阵列的解析度越多。当天线阵列发展壮大后，数组的通信性能取决 于传输信道的实际数据统计而不是像渐变正交性之类的聚合属性。最 后，引出大规模 MIMO 系统的几个结论。从理论上讲，在有无数基站 天线的多蜂窝多用户的 MIMO 系统中，快衰落的影响和不相干的噪声 都消失了。用户的数量和每个蜂窝的吞吐量与蜂窝单元的大小没有关 系，系统的性能仅受制于由导频序列的再利用而引起的蜂窝间的干扰 （导频污染）。此外，每比特传输所需的能量变得任意小，最简单的 预编码器和探测器是最佳的。 上面所说的优势和特点推动了对大规模 MIMO 的全新的理论研究。 第一次主张使用相当大的天线数组是在 Marzetta T L.的 Noncooperative cellular wireless with unlimited numbers of base station antennas 中.然后引起了广泛的关注和极大的研究兴 趣。特别是，当接收和发射的天线数量没有限制时，大规模的天线阵 列主要吸引了纯学术研究的兴趣。在理想情况下，人们得到了渐近容 量的相似律。最近，大规模 MIMO 的研究逐渐从单纯的理论学习转向 实用系统方面。论文 Noncooperative cellular wireless with
    unlimited numbers of base station antennas 展示了在逼真假设 下有无数发射天线的系统。一个有 20MHz 的带宽，但在基站间没有合 作的时分复用蜂窝系统可能有 40 多个单天线用户，每个用户在上行 链路和下行链路的净平均吞吐量都是 17MHz，该系统利用从上行导频 测量值得到的信道状态信息，有 95%的可能达到 3.6MHz 的的吞吐量。 此外，在论文 2 中，大规模 MIMO 需要多少天线的问题得到了广泛的 关注和全面的研究。 在本文中，我们着重分析了和速率的上届，关键技术的研究和大 规模 MIMO 研究热点的讨论。接下来的文章结构如下：第二节中我们 从整体系统开始分析大规模 MIMO 系统的和速率的上限，第三节中主 要是逼近这个上限的关键技术，包括信道估计，下行预编码和上行信 道检测。我们专注于他们的技术特点和研究状况。根据我们的调查和 分析，第四节列出一些未来的研究热点，第五节总结全文。 2 和速率（Sum Rate Upper Bound） 众所周知，一个 MIMO 系统的容量随着发射机和接收机两侧的天线 的最小数量呈线性增加。本质上，发射机/接收机配置越多的天线， 传输信道就可以提供更高的自由度，系统就可以得到更好的性能如更 高的链路可靠性和数据速率。但是，受制于物理约束，信号处理的能 源消耗，越来越复杂的硬件和计算，在一个物理和实际系统中的天线 的数量不能任意大。此外，如果接收和发射天线的数量趋于无穷，数 学模型的物理实现将会崩溃。例如，某些点的总接收功率会超过传输 功率，这是没有物理意义的。甚至大量的工程难题直到物理模型崩溃
    才会出现，所以，一个大规模 MIMO 系统中需要多少基站天线的问题 是迫切需要解决的。一些理论分析认为大规模的 MIMO 系统安装的天 线要比现有的系统多一个能量级，说达到一百甚至更多，论文 3 认为 大规模的 MIMO 系统至少要有一百个基站天线，但也许少于 1000 个。 另外，许多大规模 MIMO 的研究认为系统的发射和接收天线的数量是 数十到数百之间。 更直观的说，论文 4 分析了有 4 个蜂窝，每个蜂窝有 10 个单天线 用户的系统的和速率。它表明，在低信噪比情况下，可实现的速率随 着安装大量的额外基站天线显著提高。当基站天线的数量超过 100， 和速率趋于稳定，接近于有无数个基站天线的可实现的上行速率的下 界，并和信噪比无关。当基站天线继续增加时，和速率也基本保持恒 定。 对有不同天线阵列的系统，我们给出一些和速率的性能仿真结果， 如图 2.
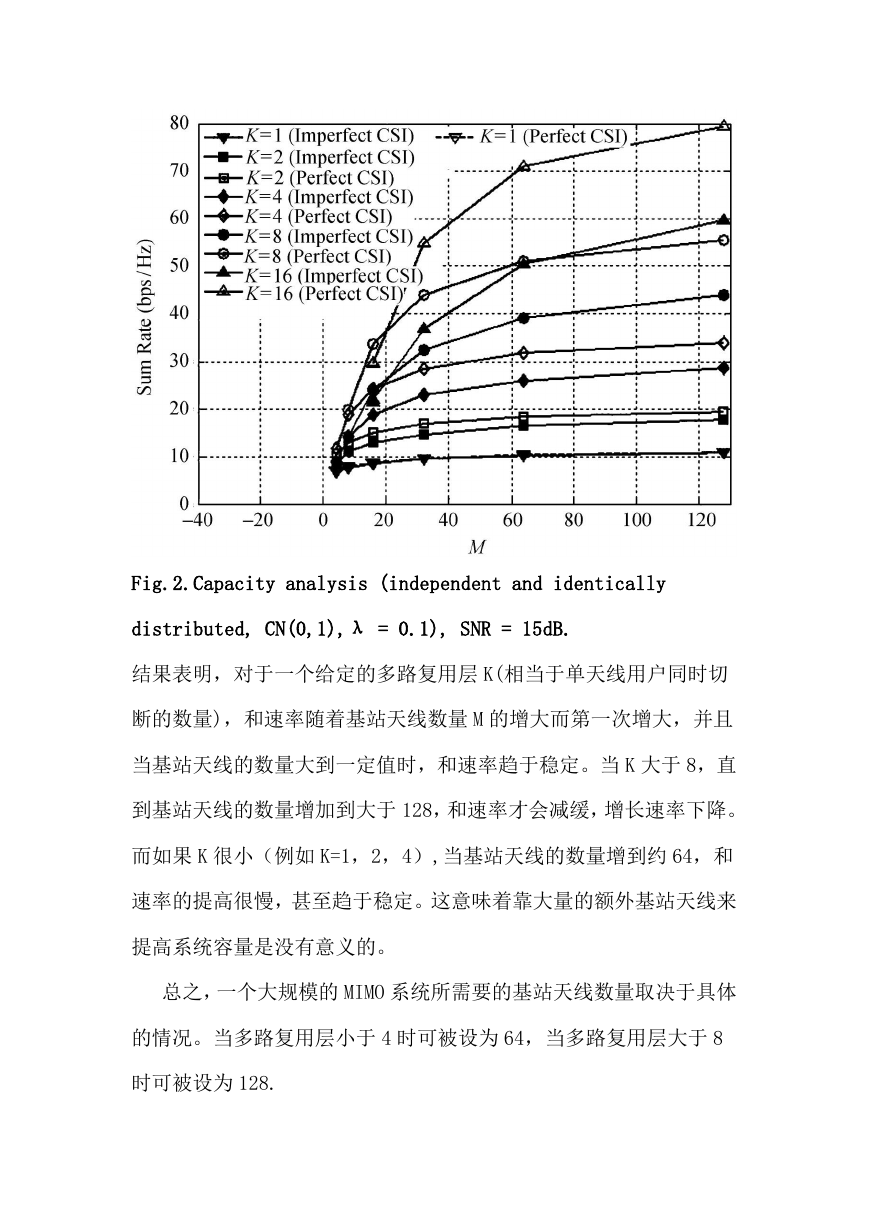
    Fig.2.Capacity analysis (independent and identically distributed, CN(0,1),λ = 0.1), SNR = 15dB. 结果表明，对于一个给定的多路复用层 K(相当于单天线用户同时切 断的数量)，和速率随着基站天线数量 M 的增大而第一次增大，并且 当基站天线的数量大到一定值时，和速率趋于稳定。当 K 大于 8，直 到基站天线的数量增加到大于 128，和速率才会减缓，增长速率下降。 而如果 K 很小（例如 K=1，2，4）,当基站天线的数量增到约 64，和 速率的提高很慢，甚至趋于稳定。这意味着靠大量的额外基站天线来 提高系统容量是没有意义的。 总之，一个大规模的 MIMO 系统所需要的基站天线数量取决于具体 的情况。当多路复用层小于 4 时可被设为 64，当多路复用层大于 8 时可被设为 128.
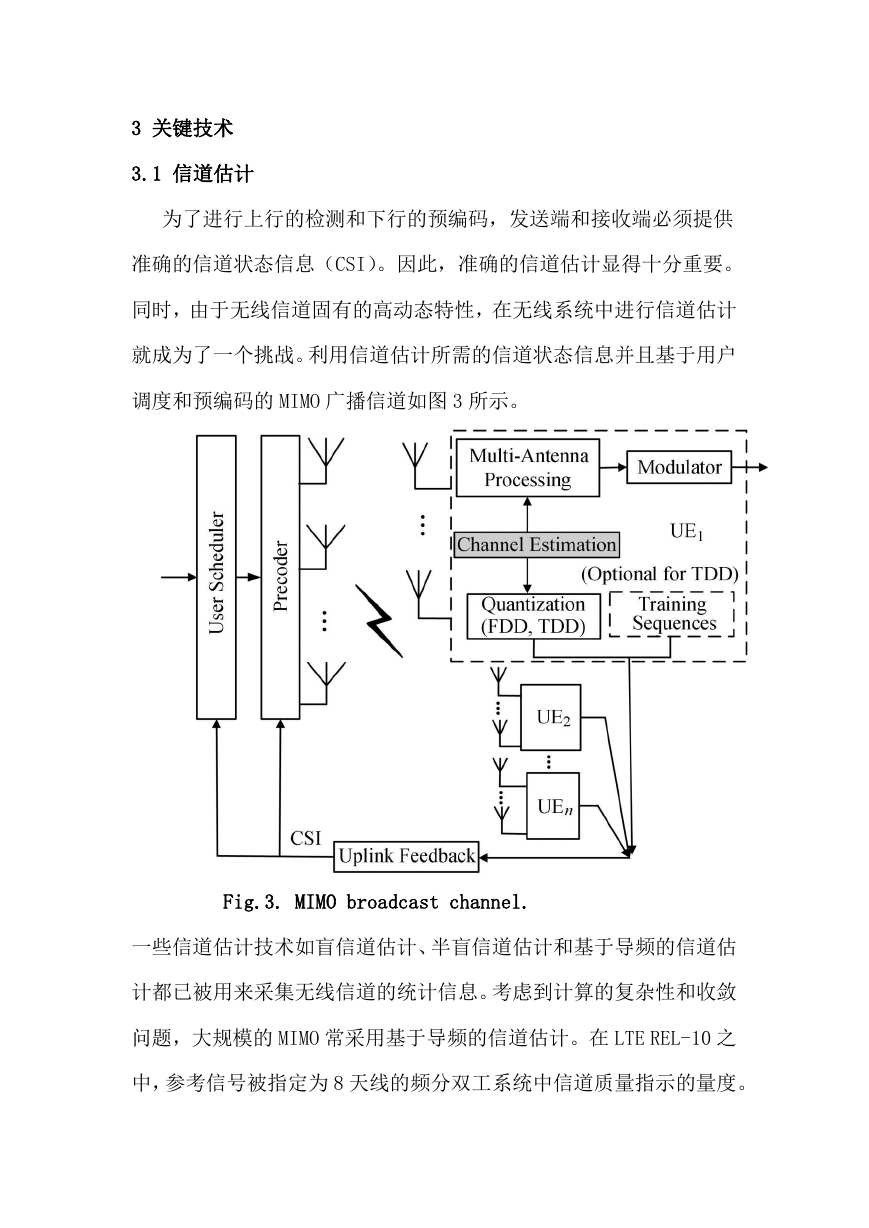
    3 关键技术 3.1 信道估计 为了进行上行的检测和下行的预编码，发送端和接收端必须提供 准确的信道状态信息（CSI）。因此，准确的信道估计显得十分重要。 同时，由于无线信道固有的高动态特性，在无线系统中进行信道估计 就成为了一个挑战。利用信道估计所需的信道状态信息并且基于用户 调度和预编码的 MIMO 广播信道如图 3 所示。 Fig.3. MIMO broadcast channel. 一些信道估计技术如盲信道估计、半盲信道估计和基于导频的信道估 计都已被用来采集无线信道的统计信息。考虑到计算的复杂性和收敛 问题，大规模的 MIMO 常采用基于导频的信道估计。在 LTE REL-10 之 中，参考信号被指定为 8 天线的频分双工系统中信道质量指示的量度。
    然而，在大规模的 MIMO 系统中基站（BS）天线的数量远大于 8。由 于参考信号的数量线性地随着 BS 天线的数量增加而增加，当 BS 天线 的数量很大的时候，将没有数据传输的资源可用。因此，在频分双工 系统中我们只好牺牲信道估计的精确度，通过减少参考信号的开销来 实现数据传输。并且应当设计出更多有效的导频图样。然而对于一个 时分双工系统而言，在一个相干区间内的不同相位如图 4 所示。 Fig.4. Different phases in a coherence interval. 信道互惠可以被用来在上行链路中训练和估计信道从而在发送端得 到准确的信道状态信息。然而，导频的污染是应当解决的。目前，通 过依赖于信道互惠的时分双工导频的信道估计的研究已经启动，关于 它的一些具体的研究对于未来而言仍然是一个问题。 此外，对于信道估计已经有很多标准被提出。在不了解信道统计 信息的情况下，最小二乘法简单准确同时有着高信噪比，但却有着很 高的均方误差。最小均方误差算法可以采用信道的二阶统计特性来使 均方误差达到最小，但缺点是复杂度随着观察样本的增加而指数性地 增加，这样会使系统更加得复杂。论文 5 提出了新简化的最小二乘 法和宽松的最小均方误差技术，因为相比于传统的最小二乘法和最小 均方误差法，其需要更少关于信道二阶统计特性的信息而得到更好的 性能。此外，有一种新的方法被提出，其使用先进的程序结合了最小
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料