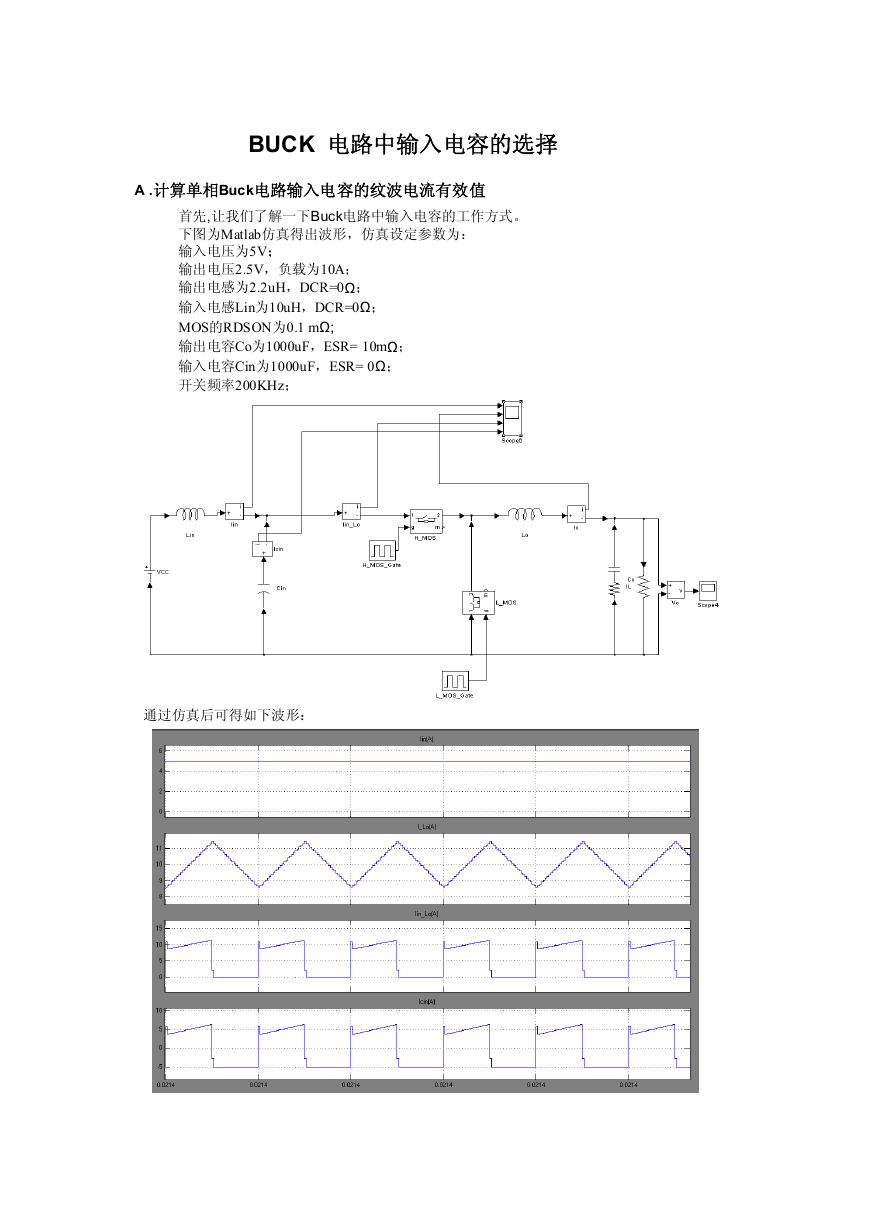
BUCK 电路中输入电容的选择 A .计算单相Buck电路输入电容的纹波电流有效值 首先,让我们了解一下Buck电路中输入电容的工作方式。 下图为Matlab仿真得出波形，仿真设定参数为： 输入电压为5V； 输出电压2.5V，负载为10A； 输出电感为2.2uH，DCR=0Ω； 输入电感Lin为10uH，DCR=0Ω； MOS的RDSON为0.1 mΩ; 输出电容Co为1000uF，ESR= 10mΩ； 输入电容Cin为1000uF，ESR= 0Ω； 开关频率200KHz； 通过仿真后可得如下波形： 

在 Buck 电路中，由于 High side MOS 工作在开关状态，使得输入电流 Iin _Lo 为断续， 从而导致了输入电容上的电流 Icin 上的纹波较大。 如以上仿真波形图所示，当 High side MOS 导通时，Iin _Lo 的电流等于电感电流 I_Lo 即 Io，此时由于输入电感不能突变，输入电容需输出能量，此时由电流节点定理可知，Icin = I_o – Iin； 当 High side MOS 截止时，Iin _Lo 的电流为 0A，此时输入电感给输入电容充电，Icin = Iin； 因此 Icin 为如图所示的纹波，若输出电感较大，则可将其电流纹波看作矩形波，并按如 下方法求得其有效值： 假设: Uin D := := 5V Uo Uin Uo := Tsw 2.5V 1 Fsw := Io := 10A Fsw := 200KHz 1. 首先Iin可近似看为一条直线，由能量守恒可知: Io ×Uo = Iin ×Uin; 因此,可得输入电流的平均值为: Iin := Uo Io⋅ Uin Iin 5 A= 2. 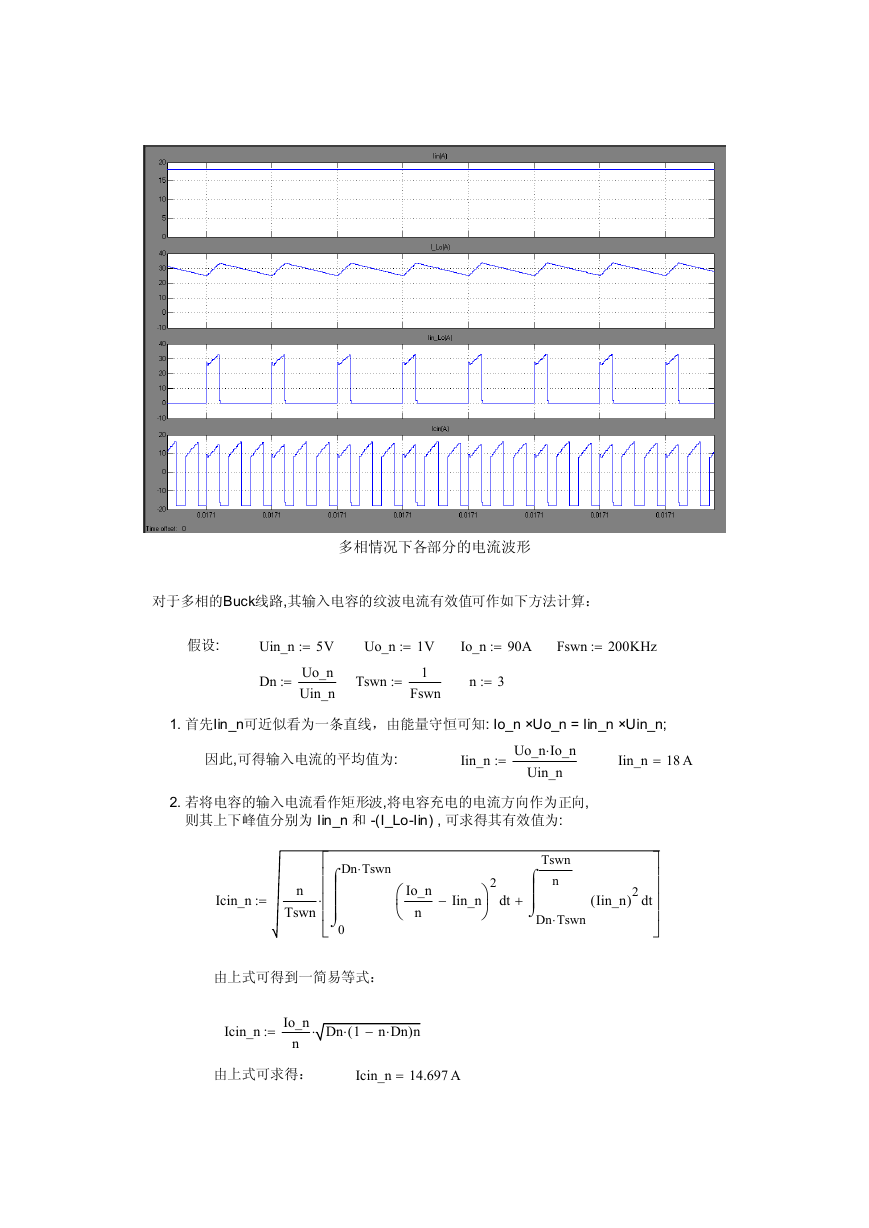若将电容的输入电流看作矩形波,将电容充电的电流方向作为正向, 则其上下峰值分别为 Iin 和 -(Io-Iin) , 可求得其有效值为: Icin := D Tsw⋅ ⌠ ⎮ ⌡ 0 ⎡⎢ ⎢ ⎣ )2 Iin− d t + ( Io Tsw ⌠ ⎮ ⌡ D Tsw⋅ )2 Iin( d t ⎤⎥ ⎥ ⎦ ⋅ 1 Tsw 由上式可得到一简易等式： Icin := Io D 1 D−( ) ⋅ ⋅ 或 Icin := Io Uo Uin Uo − ⋅ ( ⋅ Uin ) 由上式可求得： Icin 5 A= B.计算多相Buck电路输入电容的纹波电流有效值 对于 多相的Buck电路, 由其原理我们可以知道,它的输入电容上纹波 电流的频率相对于单相Buck电路来说增加了N-1倍,N是其相数。 下图为Matlab仿真得出波形，仿真设定参数为： 输入电压为5V; 输出电压1V，负载为90A; 三相的输出电感为 0.47uH，DCR=0Ω； 输入电感Lin为 1000uH，DCR=0Ω； MOS的RDSON为 0.1 mΩ; 输出电容Co为 1000uF，ESR= 5mΩ； 输入电容Cin为 1000uF，ESR= 0Ω； 开关频率 200KHz; 相数为 3相; 

多相情况下各部分的电流波形 对于多相的Buck线路,其输入电容的纹波电流有效值可作如下方法计算： 假设: Uin_n Dn := 5V := Uo_n Uin_n Uo_n := Tswn := 1V 1 Fswn Io_n := 90A Fswn := 200KHz n 3:= 1. 首先Iin_n可近似看为一条直线，由能量守恒可知: Io_n ×Uo_n = Iin_n ×Uin_n; 因此,可得输入电流的平均值为: Iin_n := Uo_n Io_n ⋅ Uin_n Iin_n = 18 A 2. 若将电容的输入电流看作矩形波,将电容充电的电流方向作为正向, 则其上下峰值分别为 Iin_n 和 -(I_Lo-Iin) , 可求得其有效值为: Icin_n := n Tswn ⎡⎢ ⎢ ⎢ ⎢⎣ ⋅ Dn Tswn ⋅ ⌠⎮ ⎮ ⎮⌡ 0 Io_n n ⎛⎜ ⎝ − Iin_n 2 ⎞⎟ ⎠ d t + Tswn n ⌠ ⎮ ⎮ ⌡ Dn Tswn ⋅ ( Iin_n )2 d t ⎤⎥ ⎥ ⎥ ⎥⎦ 由上式可得到一简易等式： Icin_n := Io_n n ⋅ Dn 1 n Dn⋅−( ⋅ )n 由上式可求得： Icin_n = 14.697 A 

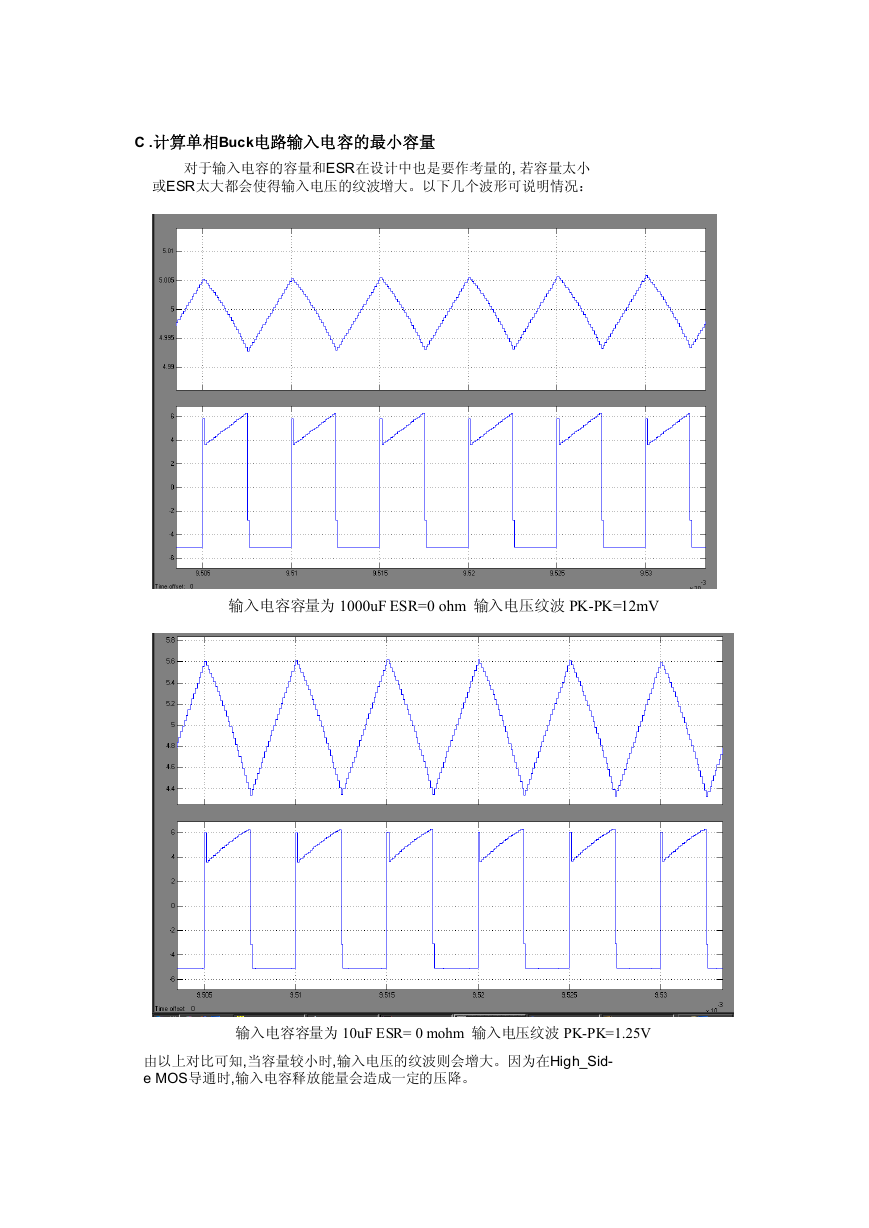
C .计算单相Buck电路输入电容的最小容量 对于输入电容的容量和ESR在设计中也是要作考量的, 若容量太小 或ESR太大都会使得输入电压的纹波增大。以下几个波形可说明情况： 输入电容容量为 1000uF ESR=0 ohm 输入电压纹波 PK-PK=12mV 输入电容容量为 10uF ESR= 0 mohm 输入电压纹波 PK-PK=1.25V 由以上对比可知,当容量较小时,输入电压的纹波则会增大。因为在High_Sid- e MOS导通时,输入电容释放能量会造成一定的压降。 

参考以上波形图,若从能量来考虑,在这段时间内输出电感上电流大约由8.5A- 上升到11.5A,而由于输入电感的存在,输入电源所提供电流不变,因此输出电 感所增加的能量为输如电容所提供.假设： := 8.5A ILo_1 11.5A 计算输出电感所增加的能量 ILo_2 := Lo := 2.2μH Ucin_1 := 5.6V Ucin_2 := 4.35V Cin := 10μF W1 := 1 2 Lo⋅ ⋅ ILo_22 − Lo⋅ ⋅ ILo_12 1 2 可算得: W1 = 6.6 × 10 5− J 计算输入电容所减少的能量 ⎞⎟ Ucin_12 ⎠ Cin W2 1 2 ⎛⎜ ⎝ := ⋅ ⋅ − 1 2 ⎛⎜ ⎝ ⋅ Cin ⋅ ⎞⎟ Ucin_22 ⎠ 可算得: W2 = 6.219 × 10 5− J 通过上式,根据输入电压的纹波PK-PK值的标准,可推得需要输入电容容量的 大小 ,具体应满足如下公式: ( − ⋅ Lo ILo_22 2 ⎞⎟ ⎠ ΔU 2 + − ⋅ ) Lo ILo_12 ΔU ⎛⎜ 2 ⎝ Ucin − 2 ⎤ ⎥ ⎦ ⎞⎟ ⎠ ΔU为输入电容的纹波要求 Cin ≥ ⎡ ⎢ ⎣ ⎛⎜ ⎝ Ucin 若输入电压掉得太多,那在一个周期内,会有一段时间PWM的占空比要增大, 对应的High_Side MOSFET的功耗要增加,尤其是当负载电流比较大的情况下 ,这些问题表现得更明显。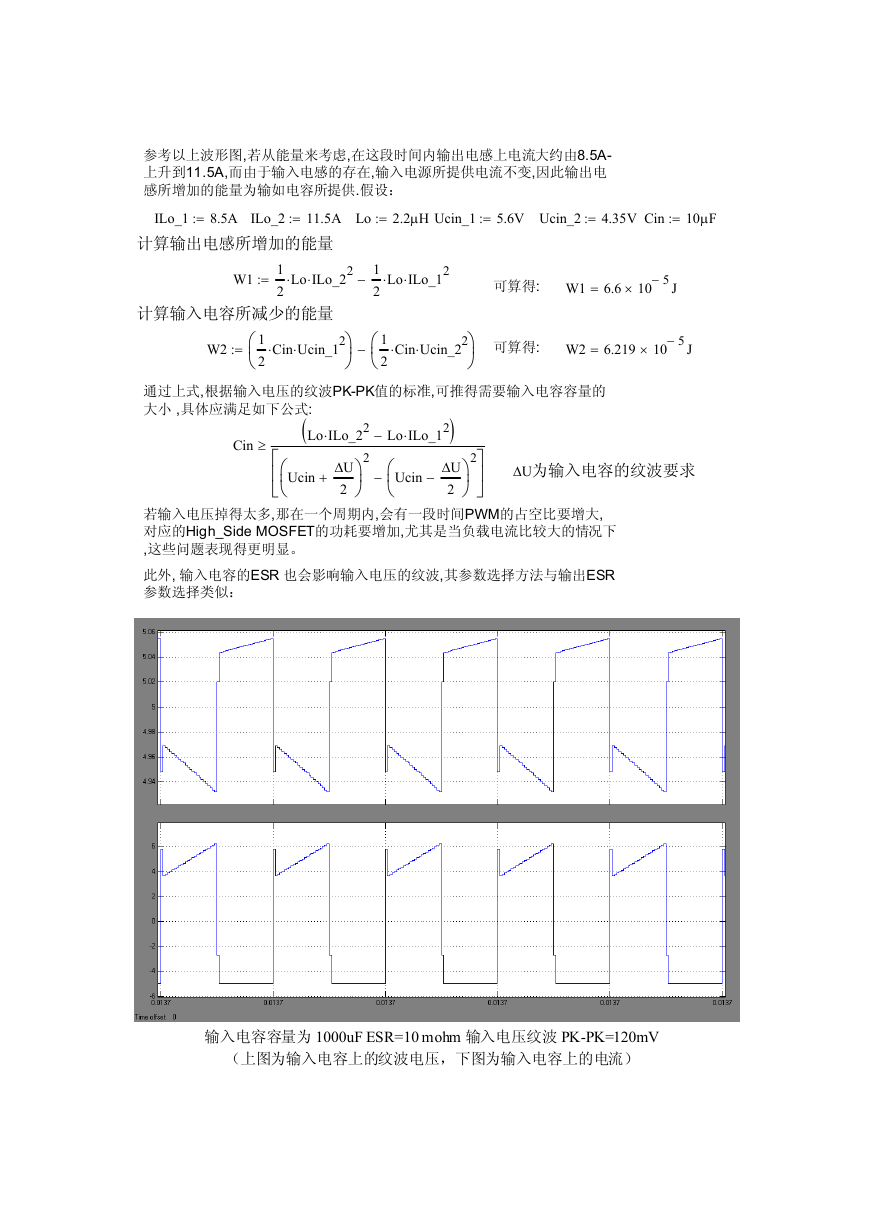 此外, 输入电容的ESR 也会影响输入电压的纹波,其参数选择方法与输出ESR 参数选择类似： 输入电容容量为 1000uF ESR=10 mohm 输入电压纹波 PK-PK=120mV （上图为输入电容上的纹波电压，下图为输入电容上的电流）