实习报告 题目：编写程序求解最小生成树 一、 需求分析 1、 本程序通过克鲁卡尔算法实现求最小生成树。最小生成树：如要在 n 个城市之间建 设通信网络，只需要架设 n-1 条线路即可。以最低的经济代价建设这个通信网。 2、 本程序的目的为用户提供城市内最低经济代价建设通信网的方案，即求解最小生成 树。根据用户提供的城市之间数据信息，为用户求解一套经济代价最低的通信网方 案。 3、 测试数据：（附后） 二、 概要设计 1、 抽象数据类型定义如下 ADT MFSet{ 数据对象：若设 S 是 MFSet 型的集合，则它由 n（n > 0）个子集 Si（i = 1,2,……,n） 构成，每个子集的成员都是子界[-maxnumber..maxnumber]内的整数； 数据关系：S1∪S2∪…∪Sn = S Si ∈ S（i = 1,2,……,n） 基本操作： Initial（&S,n） 操作结果：初始化操作。构造一个由 n 个子集（每个子集只含单个成员 xi）构 成的集合 S。 Find（S,x） 初始条件：S 是已存在的集合，x 是 S 中某个子集的成员。 操作结果：查找函数。确定 S 中 x 所属于子集 Si。 Merge（&S,i,j） 初始条件：Si 和 Sj 是 S 中的两个互不相交的非空集合。 操作结果：归并操作。将 Si 和 Sj 中的一个并入另一个中。 }ADT MFSet 2、 主程序 int main() { 初始化； While (true) { 接受命令（输入城市间信息） 处理命令； 是否退出； } 

return 0; } 3、 本程序只有两个主要模块，调用简单： 主程序模块 ——> 并查集模块 详细设计（C++源代码） 三、 #include #include #include #include using namespace std; typedef struct { int a, b; int v; }R; R r[900]; bool hash[900]; bool cmp(R a, R b) { if (a.v < b.v) return true; else return false; } void Inital(int (&S)[31], int n) { for (int i = 1; i <= n; i++) { S[i] = i; } } int Find(int S[], int x) { if (x != S[x]) return Find(S,S[x]); else return x; } void Merge(int (&S)[31], int i, int j) { S[i] = j; } 

void PrintTitle() //用户界面函数 { printf("*****************************************************\n"); printf("** printf("** printf("*****************************************************\n\n"); printf("（城市编号……n）\n\n"); printf("\t输入城市数量："); **\n"); **\n"); 实习： 最小生成树问题 } bool PrintEndTitle() //用户界面尾函数 { char temp[10]; printf("\n是否输入新数据(yes/no)："); gets(temp); if (!strcmp("no",temp)) return false; else if (!strcmp("yes",temp)) {system("cls"); return true;} else {printf("\nERROR COMMAND!\n\n"); exit(1);} } int main() { int n; int x, y, value; int S[31]; while (true) { int c = 0; PrintTitle();//用户界面函数 scanf("%d", &n); Inital(S, n); printf("\n\t输入城市间信息(输入表示结束)：\n\n"); printf("两城市编号代价\n"); while (scanf("%d%*c", &x), x) { scanf("%d%d",&y,&value); r[c].a = x; r[c].b = y; r[c++].v = value; } sort(r, r + c, cmp); memset(hash,false,sizeof(hash)); int count = 0; 

for (int i = 0; i < c; i++) { int fx = Find(S,r[i].a); int fy = Find(S,r[i].b); if (fx != fy) { Merge(S,fx,fy); hash[i] = true; count++; } if (count == n - 1) break; } printf("一套经济代价最低的通信网方案(最小生成树)：\n"); for (int i = 0; i < c; i++) { if (hash[i]) { printf("\t%d城至%d城%d代价\n",r[i].a,r[i].b,r[i].v); } } if (PrintEndTitle()) continue; //结束界面 else exit(1); } return 0; } 四、 设计和调试分析 1、 原设计是打算输入城市名字再输入代价值的形式，然后最小生成树的求解，后考虑 到文字处理的不必要性及其繁琐性，故对城市名加以编号处理，至此，城市的处理 变得简单化。 2、 程序的中心算法是克鲁卡尔算法，然后对满足最小生成树的边进行标记处理，同时 进行保存，以便后期的输出处理。 3、 总体看来此次作业比较简单，故在调试方面所需时间很少，亦无比较大的错误发生。 4、 程序的效率上，由于题目简单，而且数据范围不大，所以采用 O（n）的克鲁卡尔 算法已经比较适用。 五、 用户手册 1. 本程序运行环境为 DOS 操作系统，执行文件为 Main.exe 2. 进入程序后根据提示信息输入相应的数据即可。在输入城市之间的信息时需要用 户自己对城市进行编号，再进行输入。在下方用户界面中会有表现。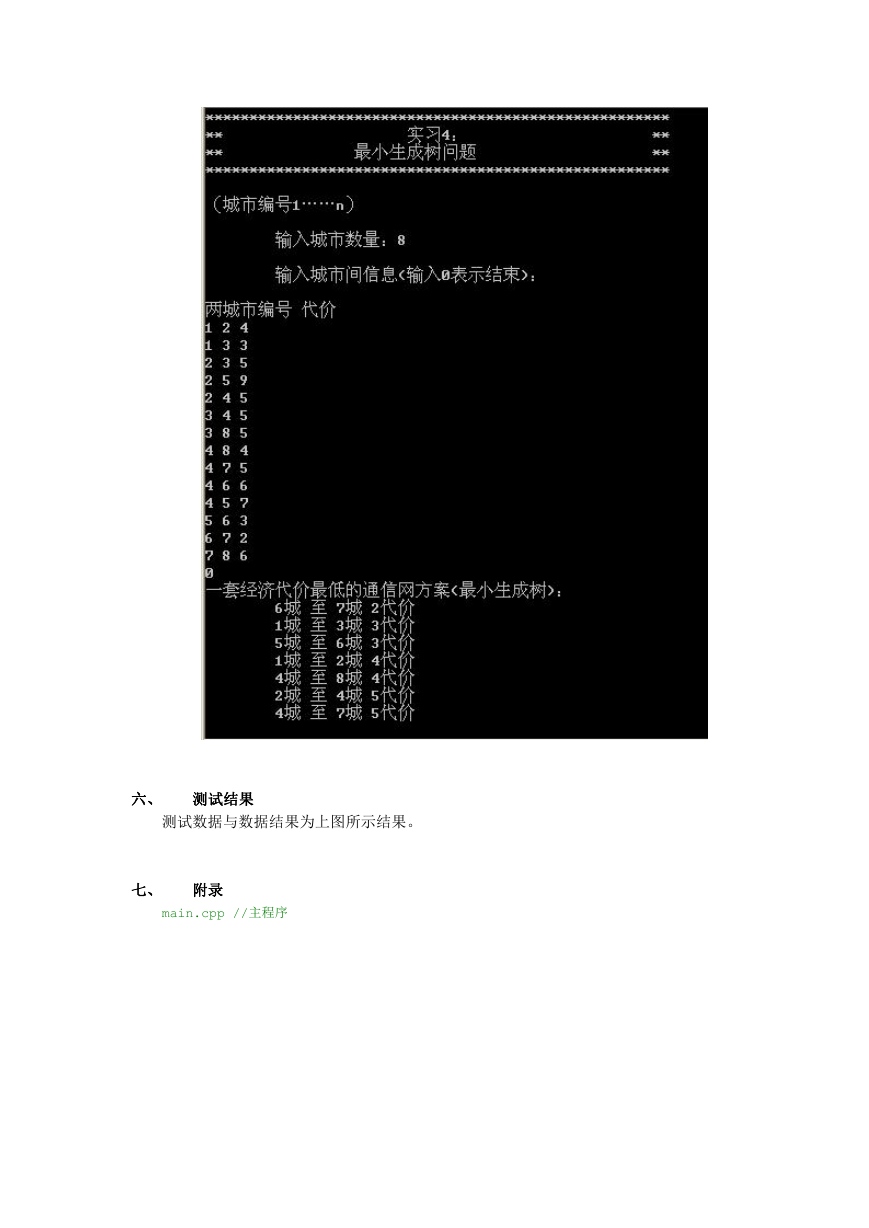 3. 用户界面 

六、 测试结果 测试数据与数据结果为上图所示结果。 七、 附录 main.cpp //主程序